Complete Solutions to EXERCISE 9.4 of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| Mathematics | EXERCISE 9.4 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
ABC is a right triangle right angled at A. BCED, ACFG and ABMN aresquares on the sides BC, CA and AB respectively. Line segment `A X_|_D E`meets BCat Y. Show that:(i) `DeltaM B C~=DeltaA B D`(ii) `a r\ (B Y X D)\ =\ 2\
View SolutionDiagonals `AC` and `BD` of a quadrilateral `ABCD` intersect each other at `P`. Show that`a r\ (A P B)\ xx\ a r\ (C P D)\ =\ a r\ (A P D)\ xx\ a r\ (B P C)dot`
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) `a r (P R Q)=1/2a r(A R C)`(ii) `a r (R Q C)=3/8a r (A B C)`(iii) `a r (P B Q) =a r (ARC)`
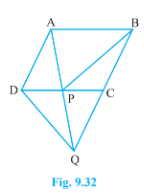
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that`A D\ =\ C Q`. If AQ intersect DC at P, show that `a r\ (B P C)\ =\ a r\ (D P Q)dot`
View SolutionIn Figure, `A B C\ a n d\ B D E` are two equilateral triangls such that `D` is the mid-point of `B CdotA E` intersects `B C` in `Fdot` Prove that: `a r( B D E)=1/4a r\ (\ A B C)`
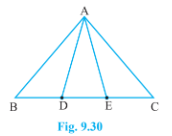
View SolutionIn Fig. 9.30, D and E are two points on BC such that `B D\ =\ D E\ =\ E C`. Show that`a r\ (A B D)\ =\ a r\ (A D E)\ =\ a r\ (A E C)`. Can you now answer the question that you have left in the Introduction of this chapter, whether the field of Budha has been actually divided into three parts of equal area ?
View SolutionIn Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that `a r (A D E) = a r(B C F)dot`
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equalareas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solution
EXERCISE 9.4 questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of NCERT MATHEMATICS(HINGLISH) of Class 9