Complete Solutions to Exercise 9.3 of chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREAS OF PARALLELOGRAMS AND TRIANGLES |
| Mathematics | Exercise 9.3 |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionIn a triangle `ABC`, `E` is the mid-point of median `AD`. Show that `a r\ (B E D)=1/4a r\ (A B C)```
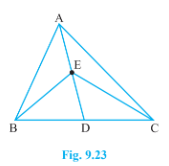
View SolutionIn Fig.9.23, E is any point on median AD of a `DeltaA B C`. Show that `a r\ (A B E)\ =\ a r\ (A C E)dot`
View SolutionD and E are points on sides AB and AC respectively of `DeltaA B C`such that`a r\ (D B C)\ =\ a r\ (E B C)`. Prove that `D E\ ||\ B C`.
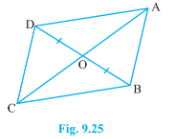
View SolutionIn Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that `O B\ =\ O D`. If `A B\ =\ C D`, then show that:(i) `a r\ (D O C)\ =\ a r\ (A O B)`(ii) `a r\ (D C B)\ =\ a r\ (A C B)`(iii) `D A\ ||\ C
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a`DeltaA B C`.Show that (i) BDEF is a parallelogram. (ii) `a r\ (D E F)=1/4a r\ (A B C)`(iii) `a r\ (B D E F)=1/2a r\ (A B C)`
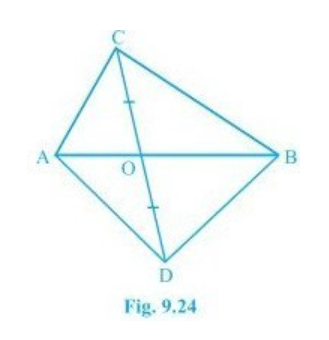
View SolutionIn Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that `ar(triangleABC)=ar(triangleABD)`
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that `a r\ (A B C D)\ =\ a r\ (P B Q R)dot`
View SolutionXY is a line parallel to side BC of a triangle ABC. If `B E\ ||\ A C`and `C F\ ||\ A B`meet XY at E and F respectively, show that `a r\ (A B E)\ =\ a r\ (A C F)`
View SolutionDiagonals `A C\ a n d\ B D` of a trapezium `A B C D` with `A B||D C` intersect each other at `O` . Prove that `a r\ ( A O D)=\ a r\ ( B O C)` .
View SolutionIn Figure, `A B C D E\ ` is a pentagon. A line through `B` parallel to `A C` meets `D C` produced at `Fdot`
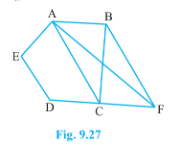
Show that: `a r\ ( A C B)=a r\ ( A C F)`
`a r\ (A E D F)=a r\ (A B C D E)`
View SolutionA villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayatof the village decided to take over some portion of his plot from one of the corners toconstruct a Health Centre. Itwaari agrees to the above proposal with the conditionthat he should be given equal amount of land in lieu of his land adjoining his plot soas to form a triangular plot. Explain how this proposal will be implemented.
View SolutionABCD is a trapezium with `A B\ ||\ D C`. A line parallel to AC intersects AB at X and BC at Y. Prove that `a r\ (A D X)\ =\ a r\ (A C Y)`.
View SolutionIn Fig.9.28, `A P\ ||\ B Q\ ||\ C R`. Prove that `a r\ (A Q C)\ =\ a r\ (P B R)dot`
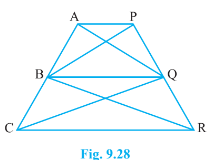
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that`a r(A O D)= a r(B O C)dot`Prove that ABCD is a trapezium.
View SolutionIn Fig.9.29, `a r\ (B D P)\ =\ a r\ (A R C)`and `a r\ (B D P)\ =\ a r\ (A R C)`. Show that both the quadrilaterals ABCD and DCPR are trapeziums.
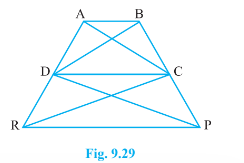
View Solution
Exercise 9.3 questions and complete solutions for chapter AREAS OF PARALLELOGRAMS AND TRIANGLES of NCERT MATHEMATICS(HINGLISH) of Class 9