Complete Solutions to प्रश्नावली 8A of chapter चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुज |
| MADHUR GUPTA | प्रश्नावली 8A |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
एक चतुर्भुज के दो कोणों `89^(@)` और `113^(@)` है। यदि अन्य दो कोण बराबर है तो बराबर कोणों को ज्ञात कीजिए।
View Solutionचतुर्भुज ABCD में `/_A=100^(@),/_B=70^(@)` और `/_C:/_D=8:11` तो `/_D` ज्ञात कीजिए।
View Solutionचतुर्भुज ABCD में भुजा AB, भुजा DC के समांतर है। यदि `/_A=/_D=1:2` और `/_C=/_B=4:5` है तो
(i) चतुर्भुज का प्रत्येक कोण ज्ञात कीजिए। (ii)चतुर्भुज ABCD का विशेष नाम दीजिए।
View Solutionसंलग्न समान्तर चतुर्भुज में x और y के मान ज्ञात कीजिए।

View Solutionनिम्नलिखित प्रत्येक आकृति से x,y और z के मान ज्ञात कीजिएः

View Solutionदी आकृति में ज्ञात कीजिएः (i) `/_XOD` (ii) `/_XOC`
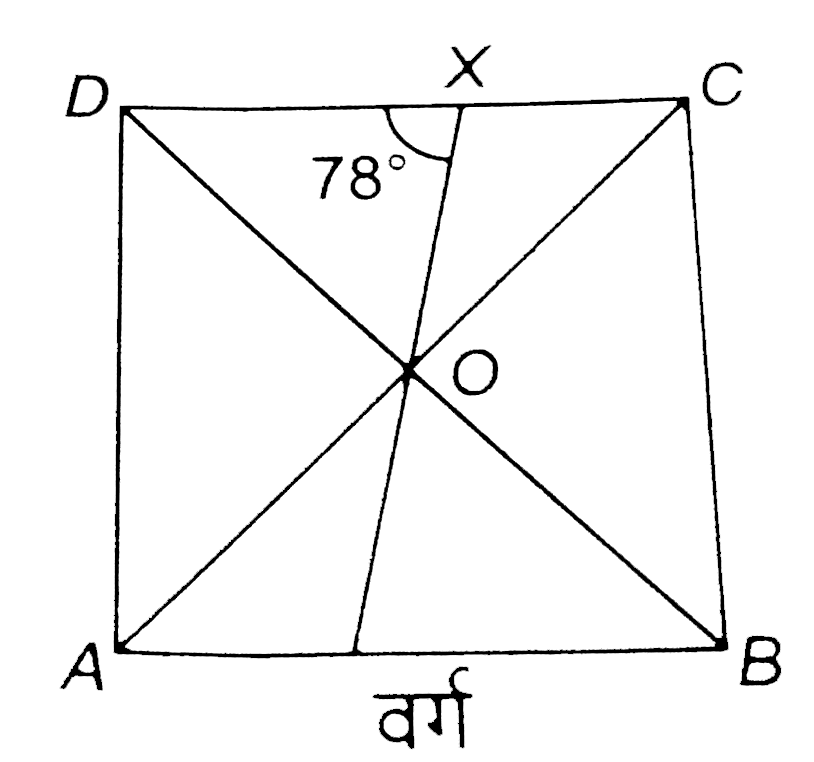
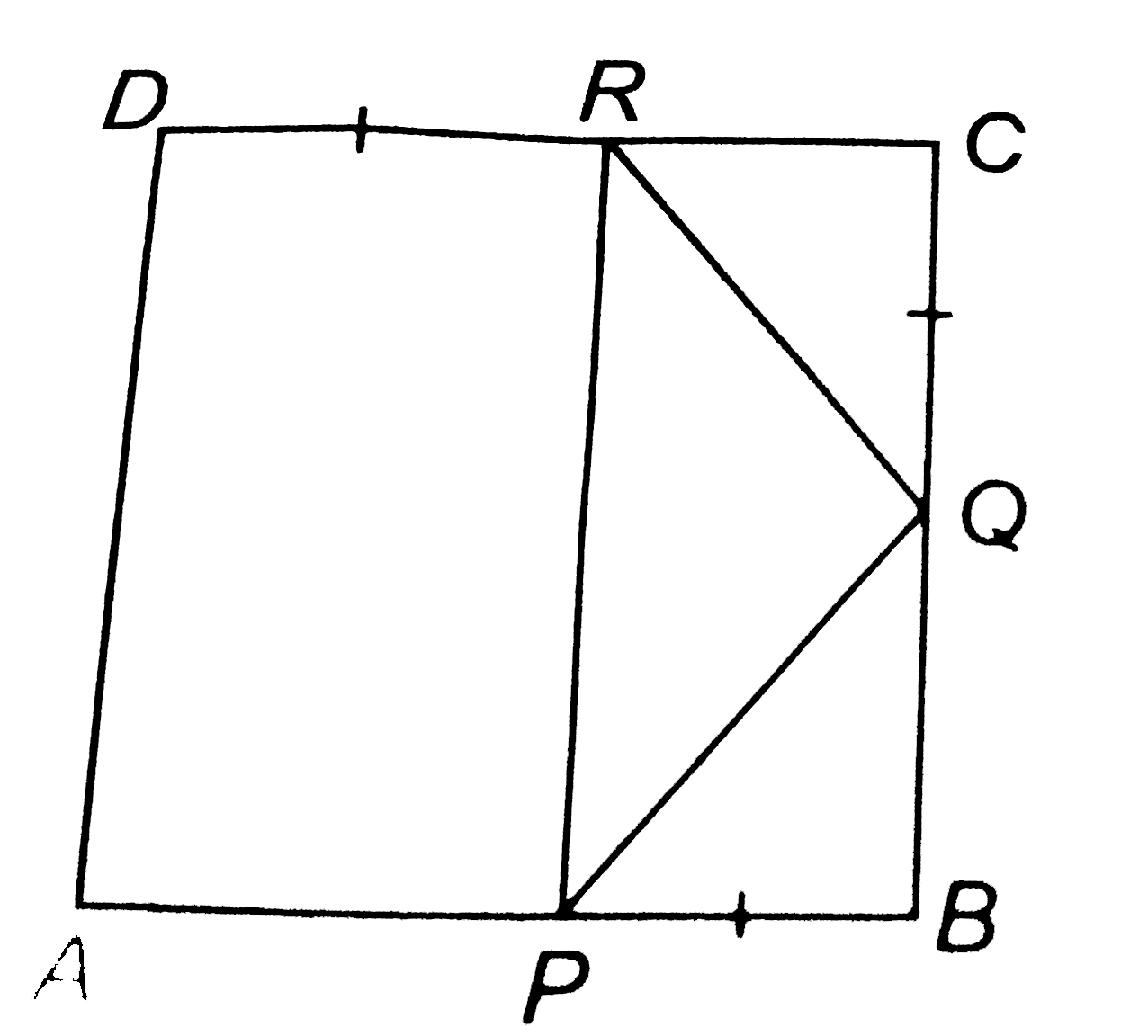
View Solutionदी आकृति में ABCD एक वर्ग है और `/_PQR=90^(@)` है। यदि `PB=QC=DR` तो सिद्ध कीजिए कि:
(i) `QB=RC`
(ii) `PQ=QR`
(iii) `/_QPR=45^(@)`
View Solutionवर्ग ABCD में विकर्ण बिंदु O पर मिलते हैं । BC पर एक बिंदु `P` इस प्रकार है कि `OB=BP` है। दिखाइए कि (i) `/_POC=(22 1/2)^(@)`
(ii) `/_BDC=2/_POC`
(iii) `/_BOP=3/_COP`
View Solutionदी आकृति में एक वर्ग `ABCD` और एक समबाहु त्रिभुज ABP दर्शाया गया है। ज्ञात कीजिएः
(i) `/_AOB` (ii) `/_BPC`
(iii) `/_PCD` (iv) प्रतिवर्त `/_APC`

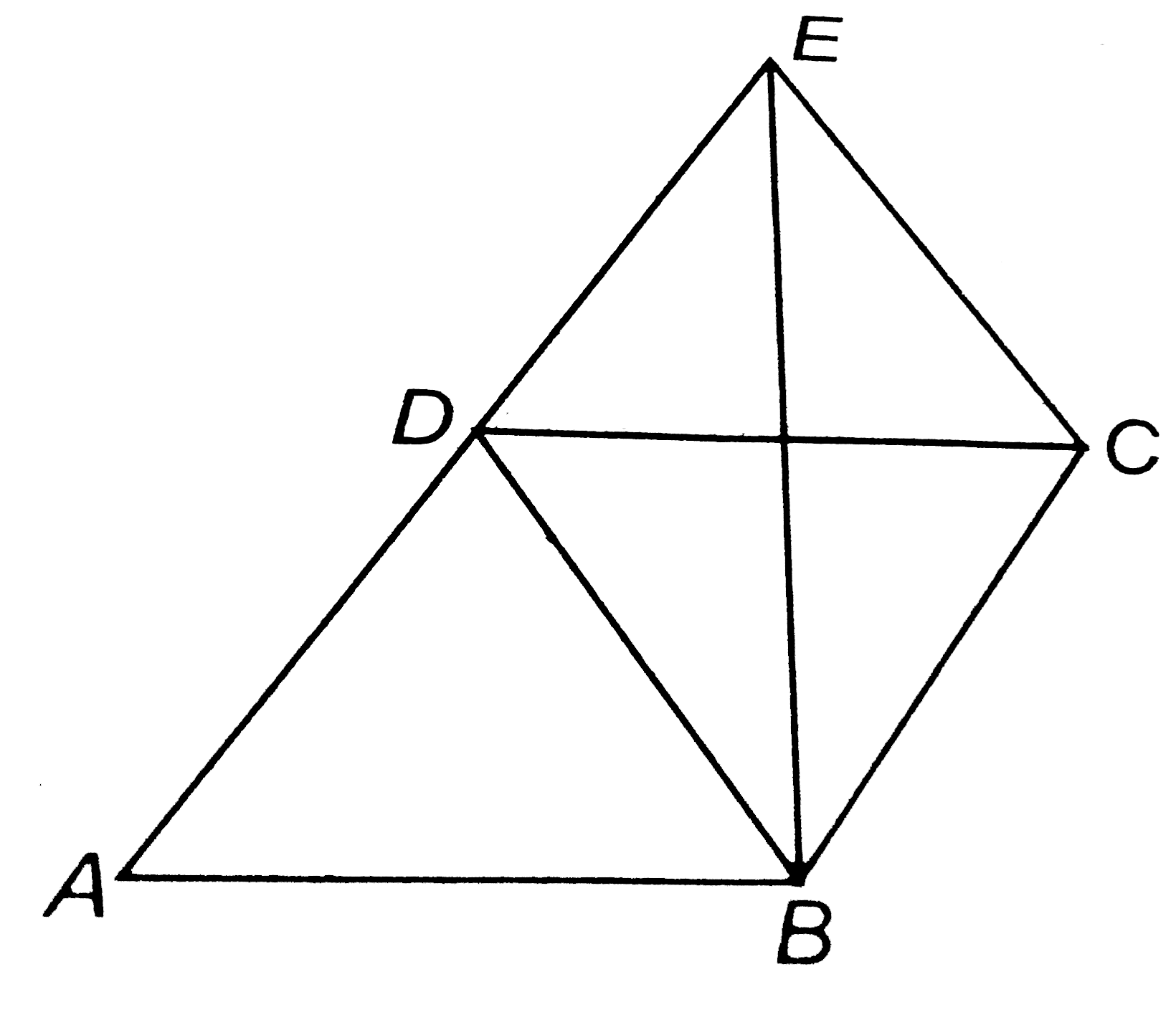
View Solutionदी गई आकृति में `ABCD` एक समचतुर्भुग्ज है जिसमें `/_A=67^(@)` है। यदि `DEC` एक समबाहु त्रिभुज है तो ज्ञात कीजिएः
(i) `/_CBE`
(ii) `/_DBE`
View Solutionएक समांतर चतुर्भुज के संलग्न कोण `1/3:1/2` के अनुपात में हैं। समांतर चतुर्भुज के सभी कोण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि समांतर चतुर्भुज के दो क्रमागत कोणों का योग `180^(@)` होता है।
View Solutionएक समांतर चतुर्भुज का एक कोण `60^(@)` है। इसके शेष कोण ज्ञात कीजिए।
View Solutionसमांतर चतुर्भुज का एक विकर्ण इसके एक कोण को समद्विभाजित करता है। दिखाइए कि यह सम्मुख कोण को भी समद्विभाजित करता है।
View Solutionएक समांतर चतुर्भुज के सम्मुख कोण `(3x-2)^(@)` और `(150-x)^(@)` है। समांतर चतुर्भुज का प्रत्येक कोण ज्ञात कीजिए।
View Solutionसंलग्न चित्र में `ABCD` एक समांतर चतुर्भुज है। यदि `/_ABC=125^(@), /_ACD=28^(@)` है तो `/_DAC` ज्ञात कीजिए।

View Solutionसमांतर चतुर्भुज का एक कोण दूसरे कोण का दुगुना है। चारों कोणों का मान ज्ञात कीजिए
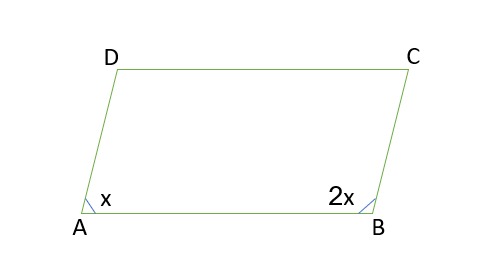
View Solutionएक समांतर चतुर्भुज ABCD में `AX` और `CY` क्रमशः `/_A` और `/_C` की समद्विभाजक रेखा है। सिद्ध कीजिए कि
`AX||CY`
View Solutionएक समांतर चतुर्भुज PQRS में `P` और `Q` से `SR` और बढ़ाई गई SR पर लम्ब क्रमशः `PX` और `QY` है। सिद्ध कीजिए कि `PX=QY`
View Solutionएक समांतर चतुर्भुज ABCD में `/_A` की समद्विभाजक रेखा `BC` को बिंदु `X` पर समद्विभाजित करती है । सिद्ध कीजिए कि `AD=2AB`
View Solutionसंलग्न चित्र में `DeltaABC` की भुजाओं `AB,BC` और `CA` के समांतर रेखाओं क्रमशः PQ,RP और QR से `DeltaPQR` बनाया गया है । सिद्ध कीजिए कि-
`PQ+QR+RP=2(AB+BC+CA)`
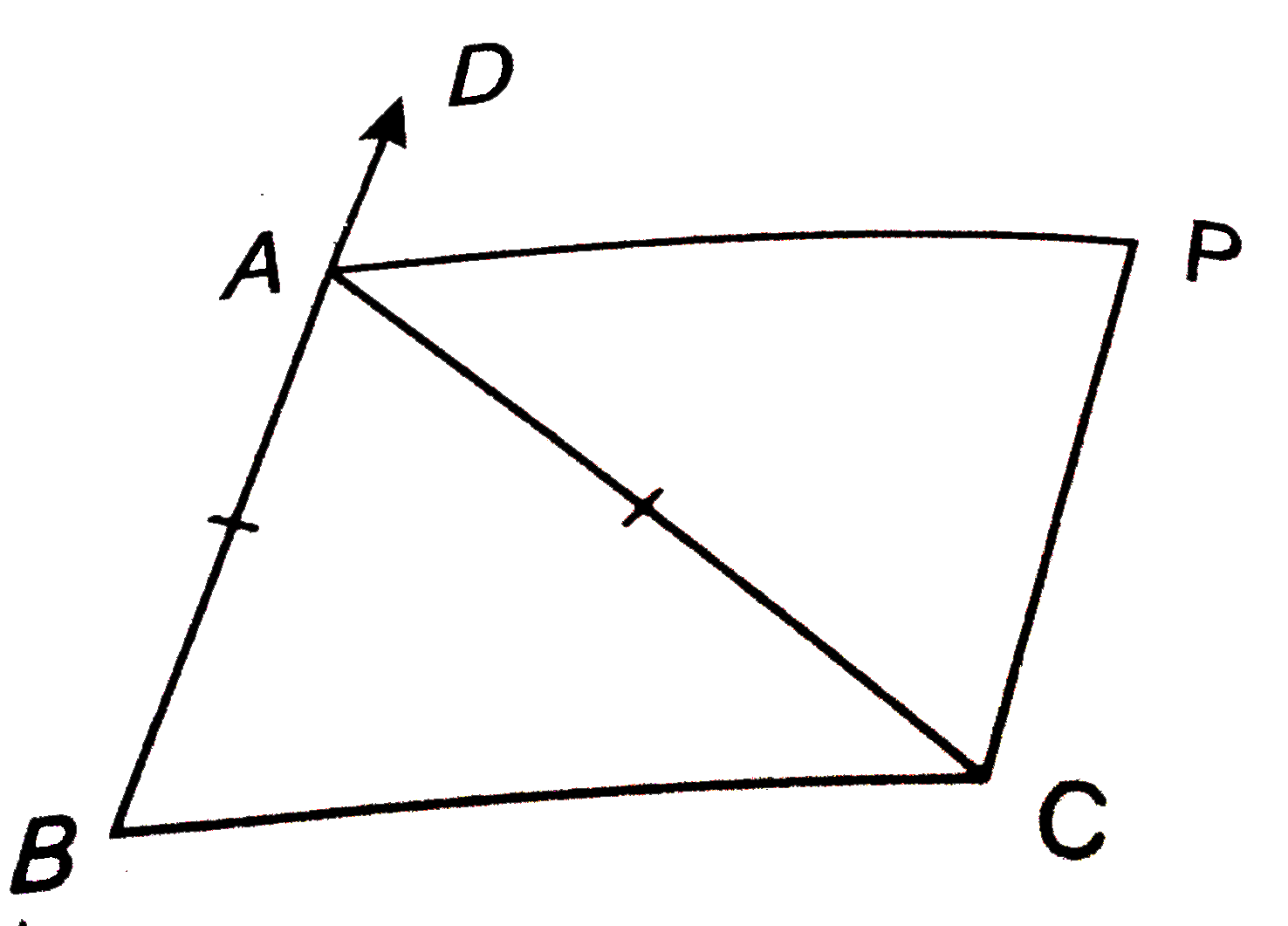
View Solutionएक समांतर चतुर्भुज ABCD की सम्मुख भुजाओं `AB` और `DC` के मध्य बिंदु क्रमशः X और Y है। सिद्ध कीजिए कि `square AXCY` एक समांतर चतुर्भुज है।
View Solutionएक समांतर चतुर्भुज के विकर्ण BD पर दो बिंदु X और Y इस प्राकार है कि `DX=BY` सिद्ध कीजिए कि `square AXCY` एक समांतर चतुर्भुज है।
View SolutionAB और CD दो समांतर रेखाएं है तथा एक तिर्यक रेखा `l` रेखाओं AB और CD को क्रमशः X और Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि अंतः कोणों के समद्विभाजक एक समांतर चतुर्भुज बनाते है, जिसके सभी कोण `90^(@)` है।
View Solutionसंलग्न चित्र में `squareABCD` एक समांतर चतुर्भुज हैं बिंदु X और Y क्रमशः भुजाओं AB और BC पर स्थित है तथा `AX=1/4AD` और `CY=1/4BC` है। दिखाइए कि `squareXBYD` एक समांतर चतुर्भुज है।
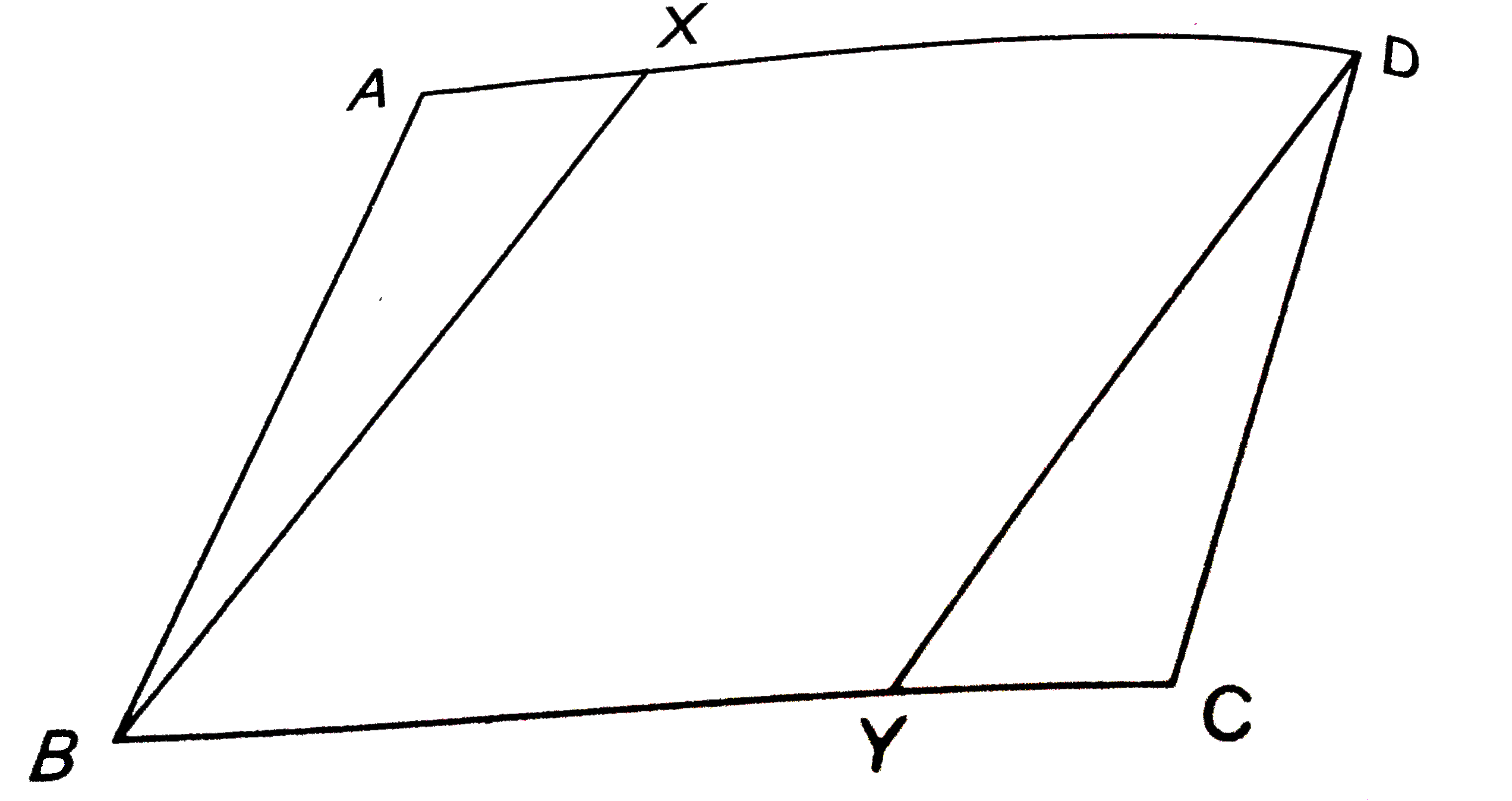
View Solutionसंलग्न चित्र में ABCDEF एक समषट्भुज हैं। सिद्ध कीजिए कि `squareABDE, squareACDF` और `squareAGDH` समांतर चतुर्भुज है।

View Solution`DeltaABC` और `DeltaDEF` दो त्रिभुज इस प्रकार है कि `AB,BC` क्रमशः `DE,EF` के समांत और बराबर है। दिखाइए कि `AC,DF` के बराबर और समांतर है।
View Solution
प्रश्नावली 8A questions and complete solutions for chapter चतुर्भुज of NAGEEN MATHS (HINDI) of Class 9