Complete Solutions to प्रश्नावली 8.1 of chapter चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | चतुर्भुज |
| MADHUR GUPTA | प्रश्नावली 8.1 |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
एक चतुर्भुज के कोण `3:5:9:13` के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
View Solutionयदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
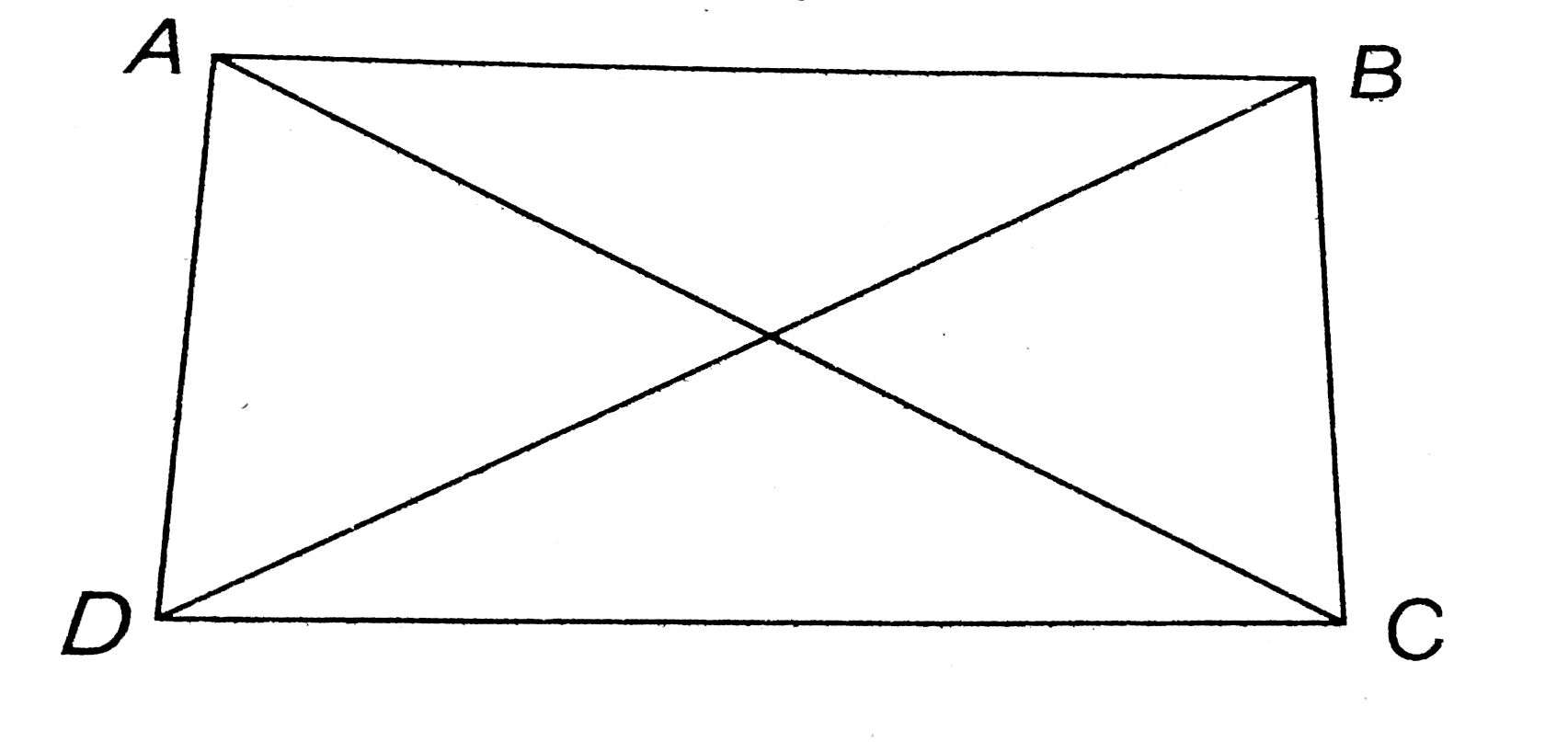
View Solutionदर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
View Solutionदर्शाइए कि एक वर्ग के विकर्ण बराबर होते है। और परस्पर समकोण पर समद्विभाजित करते हैं।
View Solutionदर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर लम्बवत समद्विभाजित करें तो वह एक वर्ग होता है।
View Solutionसमांतर चतुर्भुज ABCD का विकर्ण `AC,/_A` को समद्विभाजित करता है। दर्शाइए कि:
(i) यह `/_C` को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
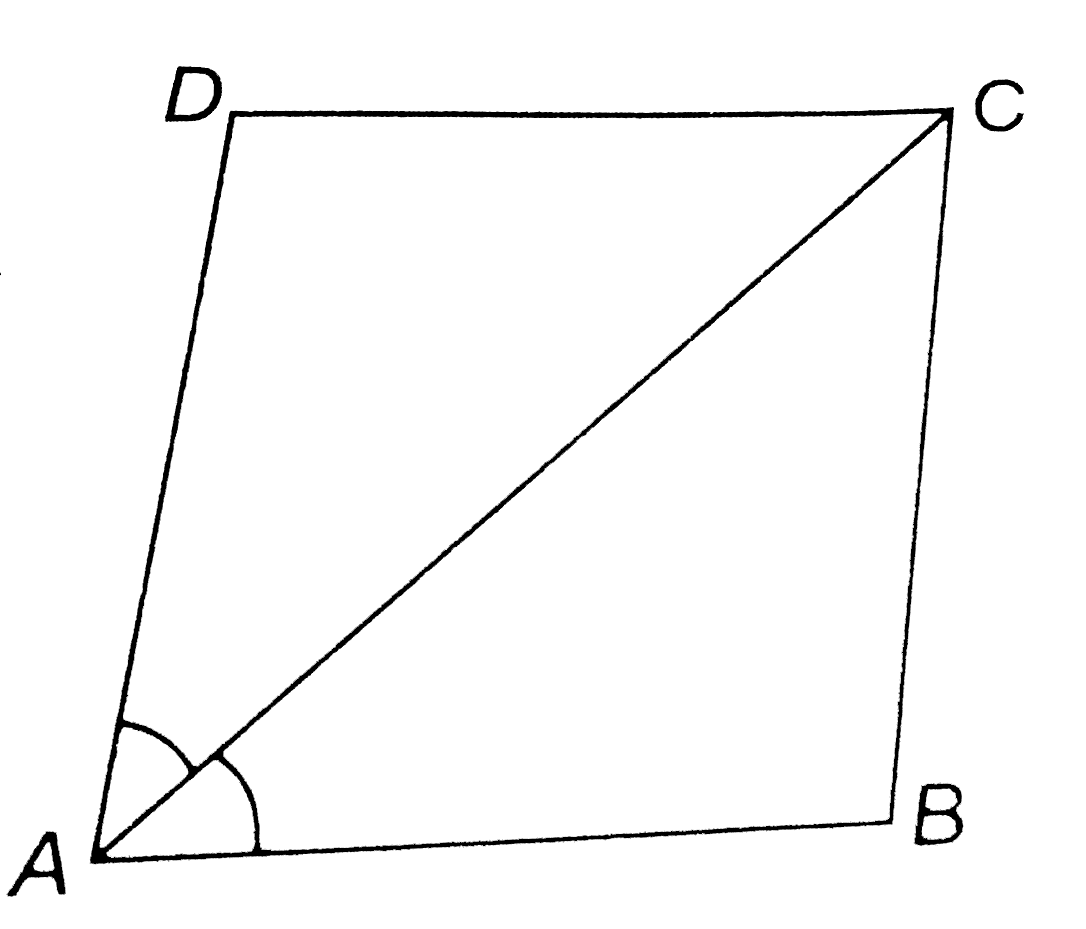
View SolutionABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों को समद्विभाजित करता है।

View Solutionदिया है:
`ABCD` एक आयत है।
`:.AB=CD` और `BC=AD`…………..1
सिद्ध करना है:
(i) `ABCD` एक वर्ग है।
अर्थात
`AB=BC=CD=DA`
(ii) विकर्ण `BD,/_B` और `/_D` दोनों को समद्विभाजित करता है।
उपपत्ति :
(i) `DeltaADC` और `DeltaABC` में
`AB||DC` और तिर्यक रेखा AC इनको काटती है।
`:'{(/_DAC=/_BAC),(/_DCA=/_BCA),(AC=CA):}` (उभयनिष्ठ)
`:.DeltaADC=DeltaABC` (A.S.A. से )
`:.AD=AB` (c.p.c.t)
और `CD=BC`…………2
अतः समीकरण 1 और 2 से
`AB=BC=AD=CD`
`:.ABCD` एक वर्ग है।
(ii) `DeltaAOB` और `DeltaCOB` में
`:'{(AB=BC),(BO=OB),(OA=OC):}`(एक वर्ग की भुजाएं)
(उभयनिष्ठ)
( `:'` वर्ग के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
`:.DeltaAOB=DeltaCOB`
(S.S.S. से )
`:./_OBA=/_OBC`
(c.p.c.t)
अतः BO या `BD,/_B` को समद्विभाजित करती है।
इसी प्रकार `DeltaAOD` और `DeltaCOD` में
`:'{(AD=CD),(OD=DO),(OA=OC):}` (वर्ग की भुजाएं)
(उभयनिष्ठ)
( `:'` वर्ग के विकर्ण एक-दूसरे की समद्विभाजित करते है।)
`:.DeltaAOD=DeltaCOD`
(S.S.S से)
`:./_ADO=/_CDO`
अतः `DO` या `DB,/_D` को समद्विभाजित करती है।
View Solutionसमांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु `P` और `Q` इस प्रकार स्थित हैं कि `DP=BQ` है। दर्शाइए कि:
(i) `DeltaAPD~=DeltaCQB` (ii) `AP=CQ`
(iii) `DeltaAQB~=DeltaCPD` (iv) `AQ=CP`
(v) `APCQ` एक समांतर चतुर्भुज है।
View SolutionABCD एक समांतर चतुर्भुज है तथा `AP` और `CQ` शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं
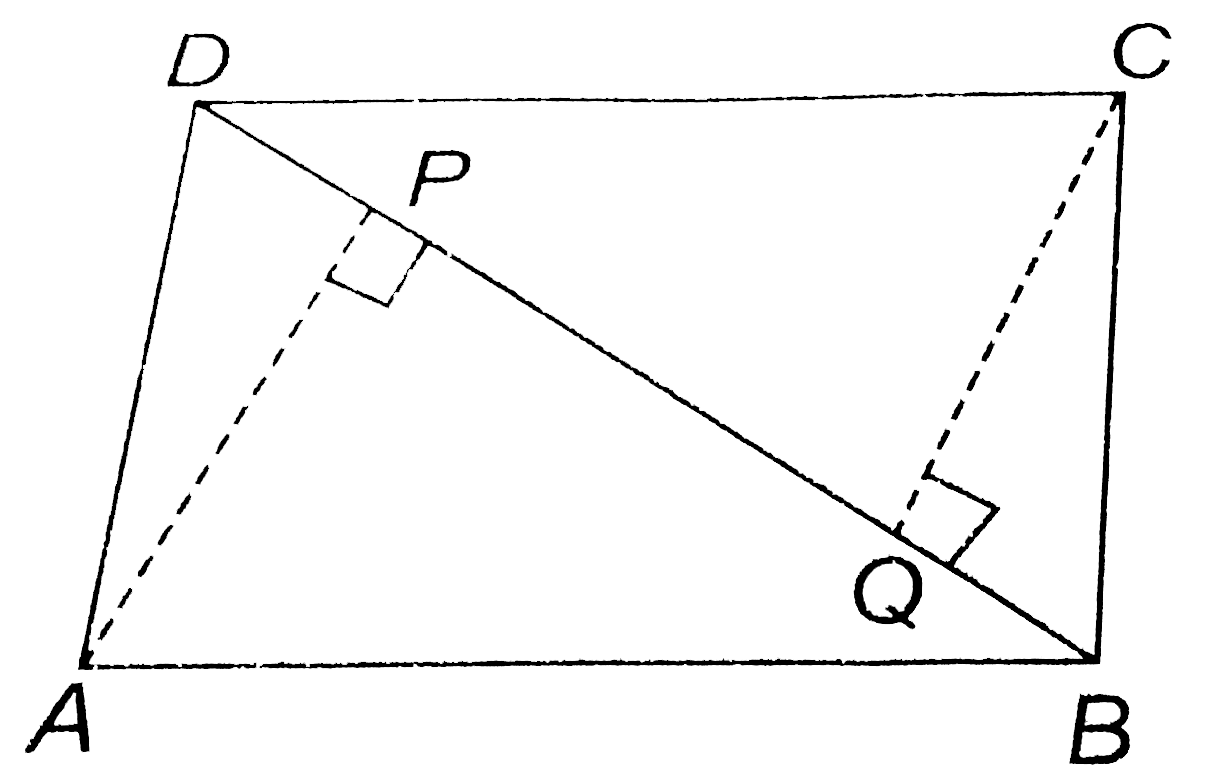
(i) `DeltaAPB~=DeltaCQD`
(ii) `AP=CQ`
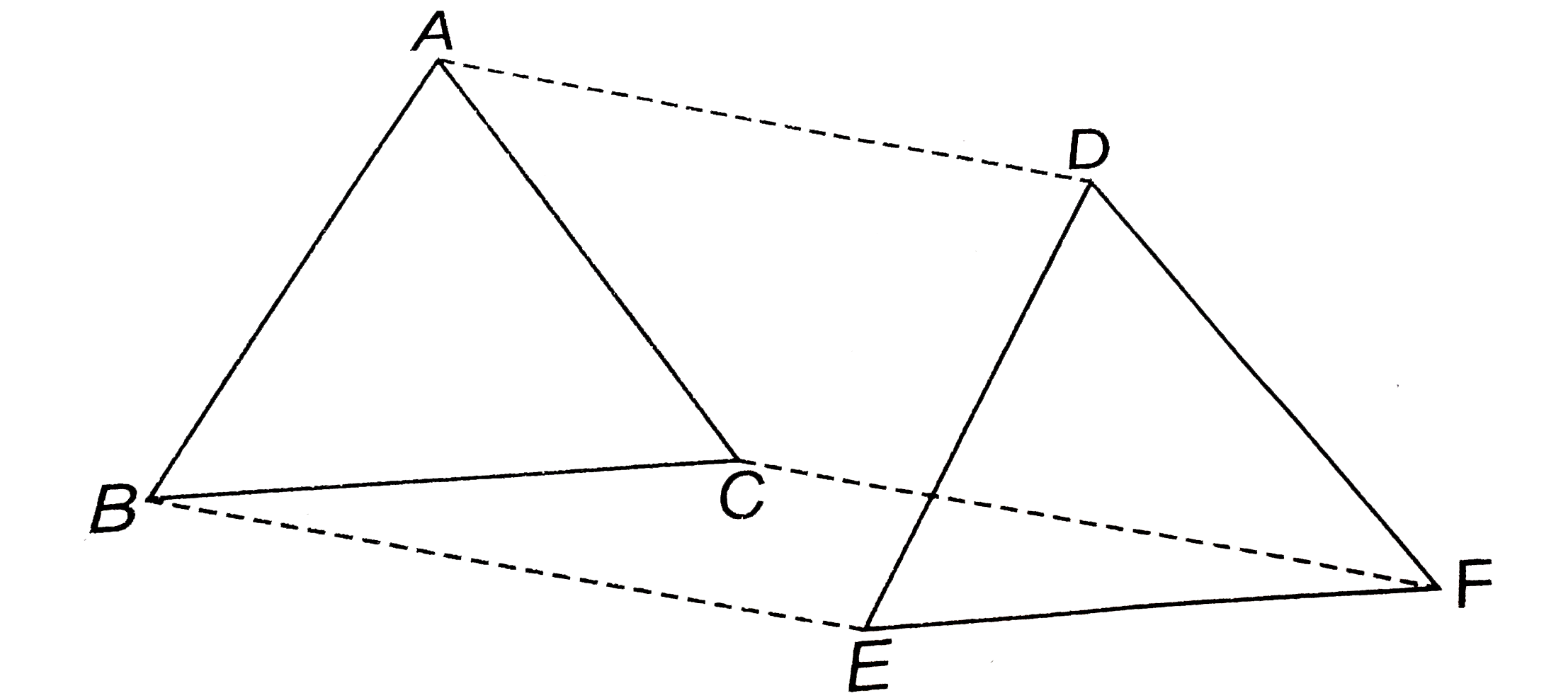
View Solution`DeltaABC` और `DeltaDEF` में `AB=DE,AB||DE,BC=EF` और `BC||EF` हैं शीर्षों A,B और C को क्रमशः शीर्षों D,E और F से जोड़ा जाता है।
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) `AD||CF` और `AD=CF` है।
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) `AC=DF` है।
(vi) `DeltaABC~=DeltaEF` है।
View SolutionABCD एक समलम्ब है जिसमें `AB||DC` और `AD=BC` है। दर्शाइए कि:
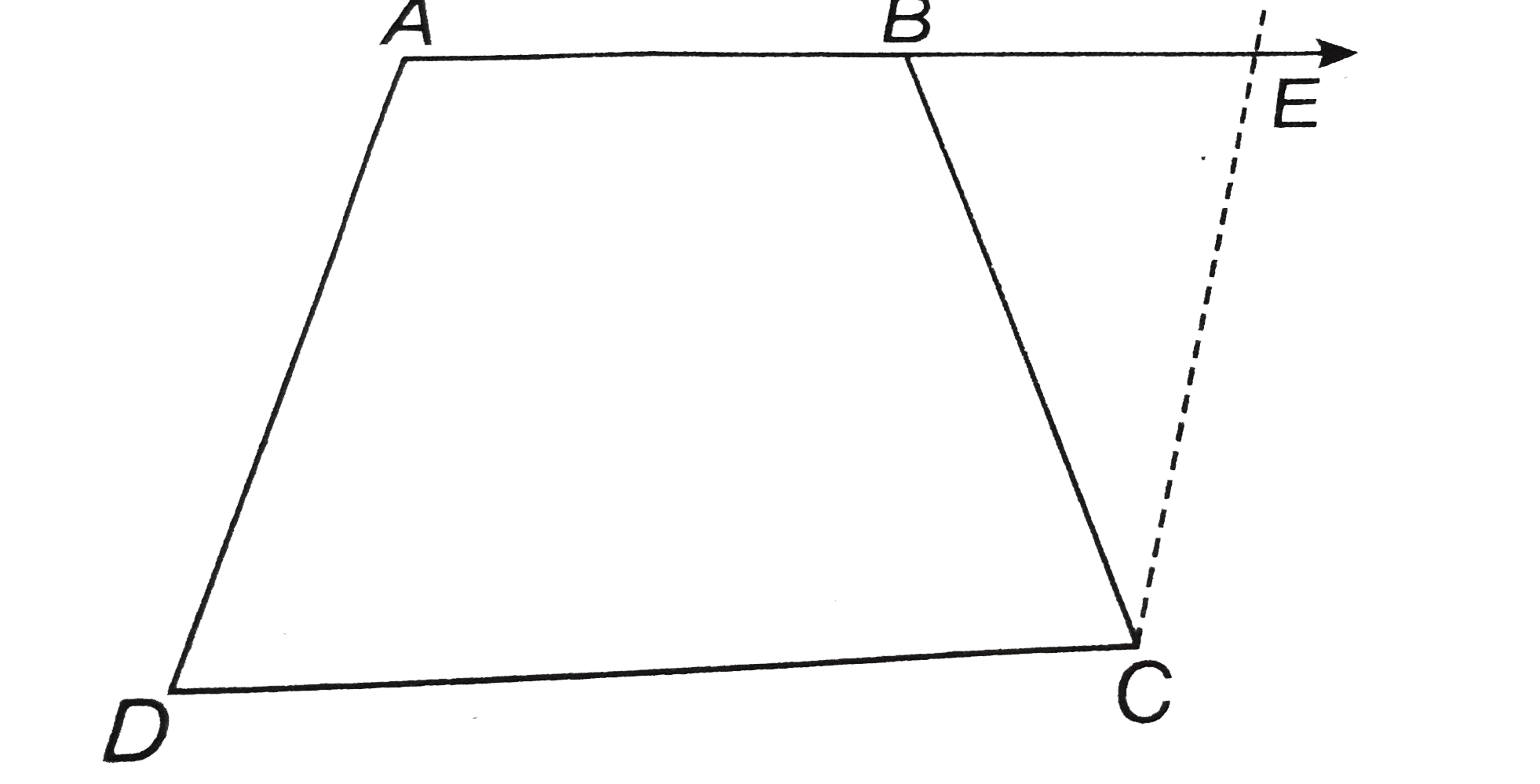
(i) `/_A=/_B`
(ii) `/_C=/_D`
(iii) `DeltasABC=DeltaBAD`
(iv) विकर्ण `AC=` विकर्ण `BD` है।
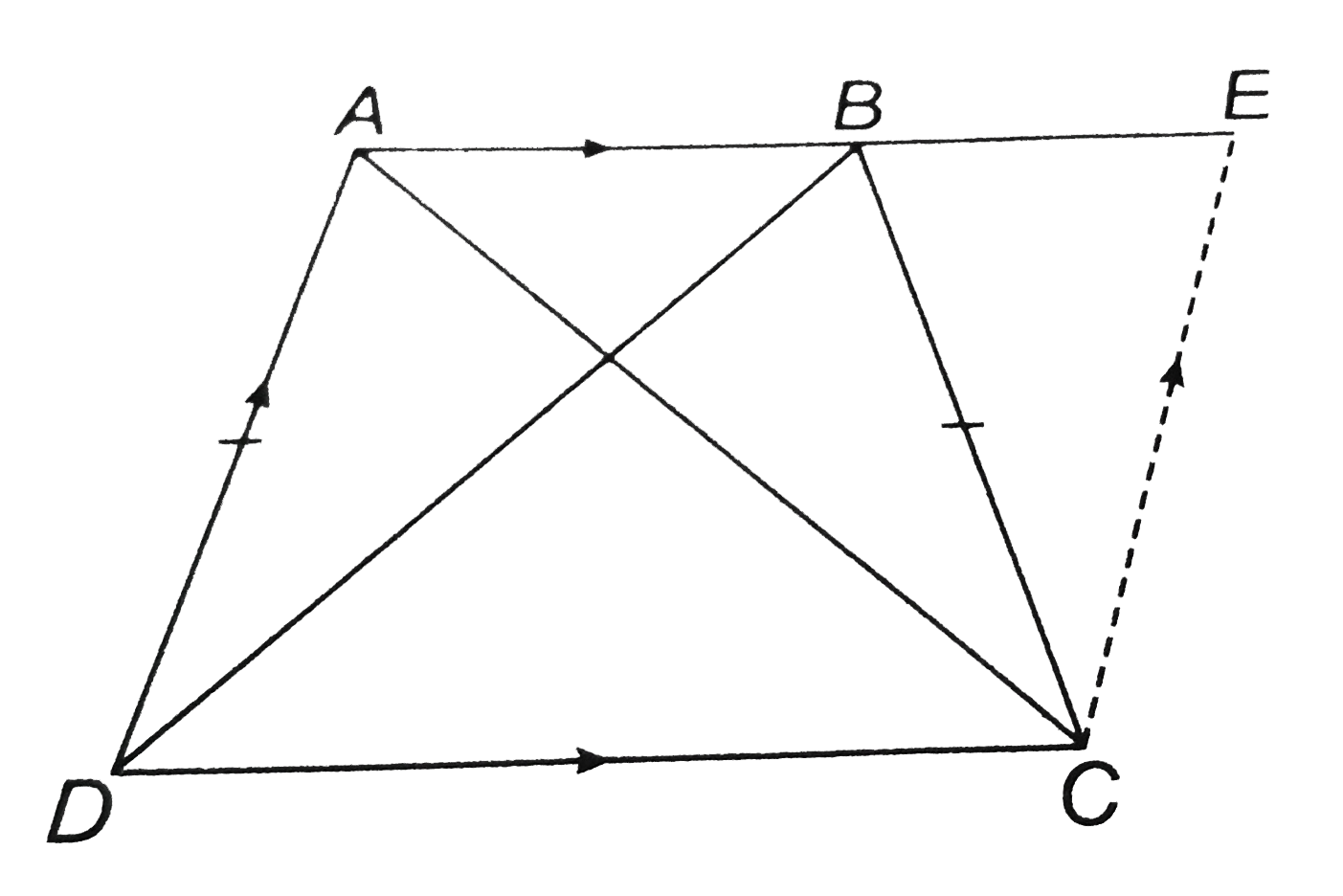
View Solution
प्रश्नावली 8.1 questions and complete solutions for chapter चतुर्भुज of NAGEEN MATHS (HINDI) of Class 9