Complete Solutions to SHORT ANSWER TYPE QUESTIONS of chapter GEOMETRY of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | GEOMETRY |
| PEARSON IIT JEE FOUNDATION | SHORT ANSWER TYPE QUESTIONS |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
In the following figure, `PQ || RS`, if `angleTRS=105^(@)`, `anglePTR=35^(@), angleQPT=a^(@)`, find the value of a.

View SolutionIn a triangle ABC, `angleA lt angleB, angleB gt angleC` and `angleA=2angleC`, prove that `AC gt BC gt AB`.
View SolutionIf two complementary angles are in the ratio `7:11`, find the supplement of the bigger angle.
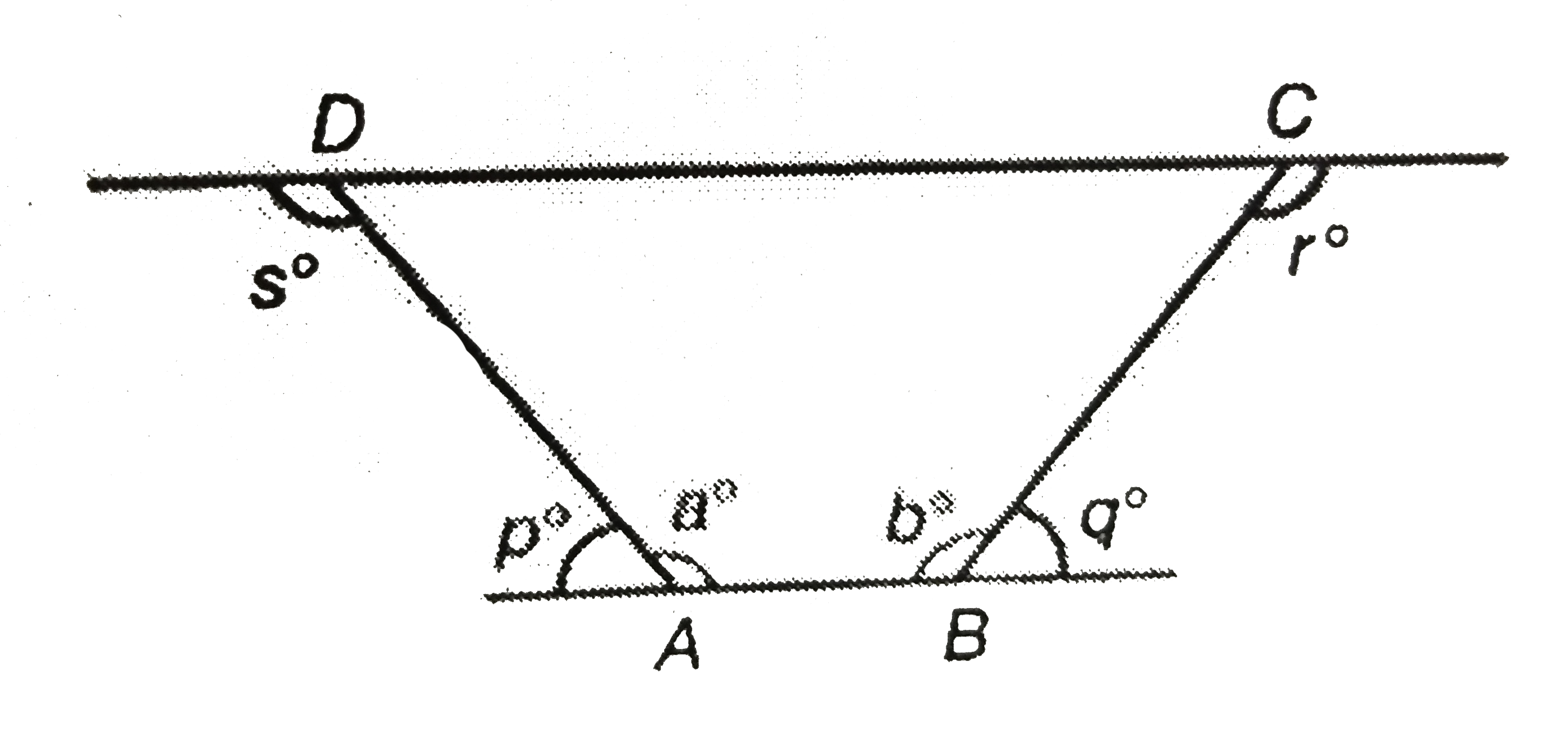
View SolutionIn the given quadrilateral ABCD , `p^(@)+ q^(@)=100^(2)`, `a^(@)=140^(@)` and `r^(@)=1/2(a^(2)+q^(@))`. Find the angles `p^(@), q^(@), r^(@)` and `s^(@)`.
View SolutionIn the following figure, BE is the diameter of the circle. Find the value of `x` and `angleDAB`.

View SolutionIn the following figure, `bar(CB)` is produced to the point A. Find `angleBDC`.

View SolutionIf the sum of the interior angles of a polygon is `2340^(@)`, then find the number of sides of the polygon.
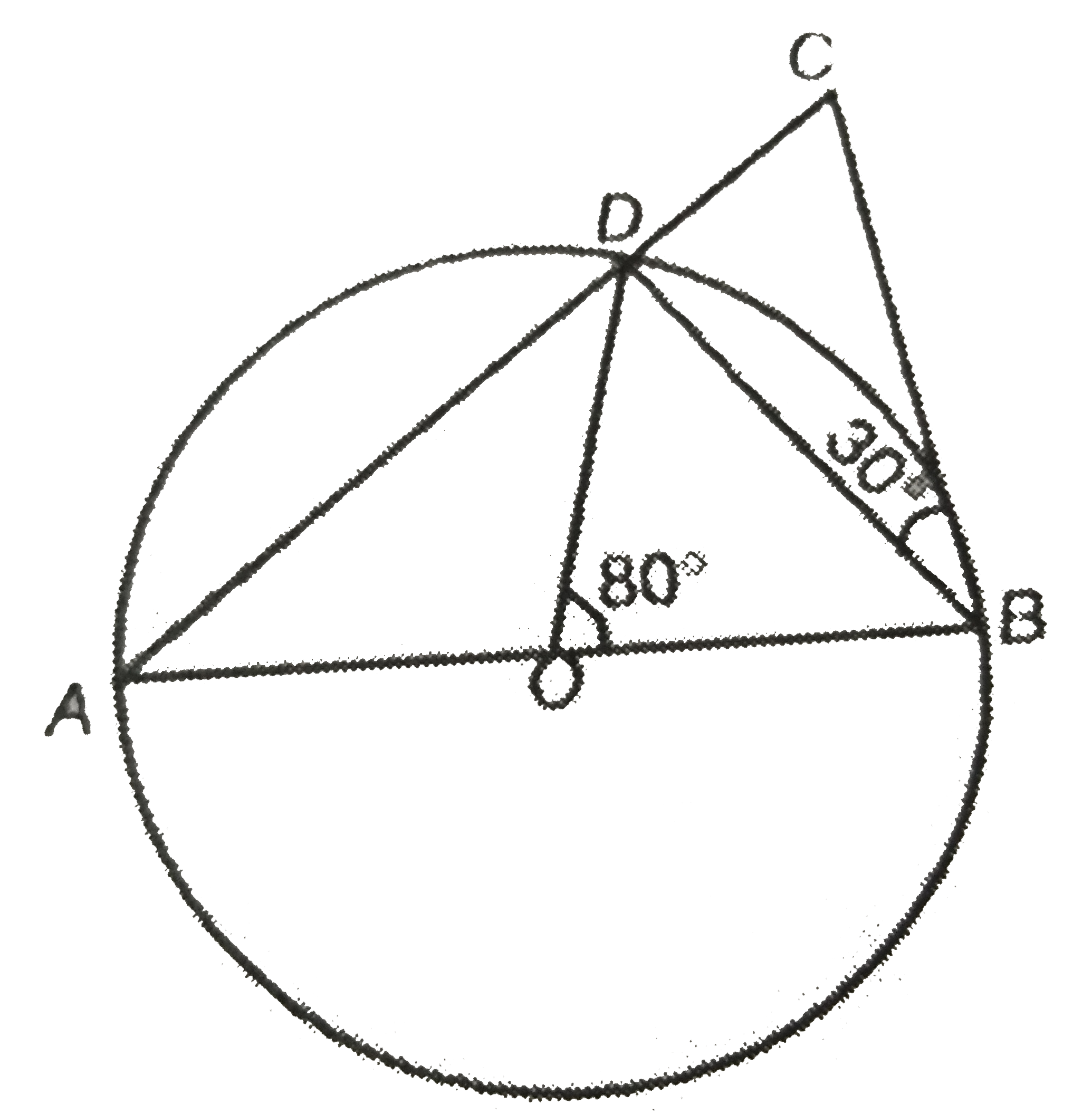
View SolutionIn the following figure, if O is the center of the circle and `bar(AB)` is the diameter, then find `angleACB`.
View Solution
In the above figure, find the values of z, if `x` is two-third of y which is a complement of `45^(@)`.
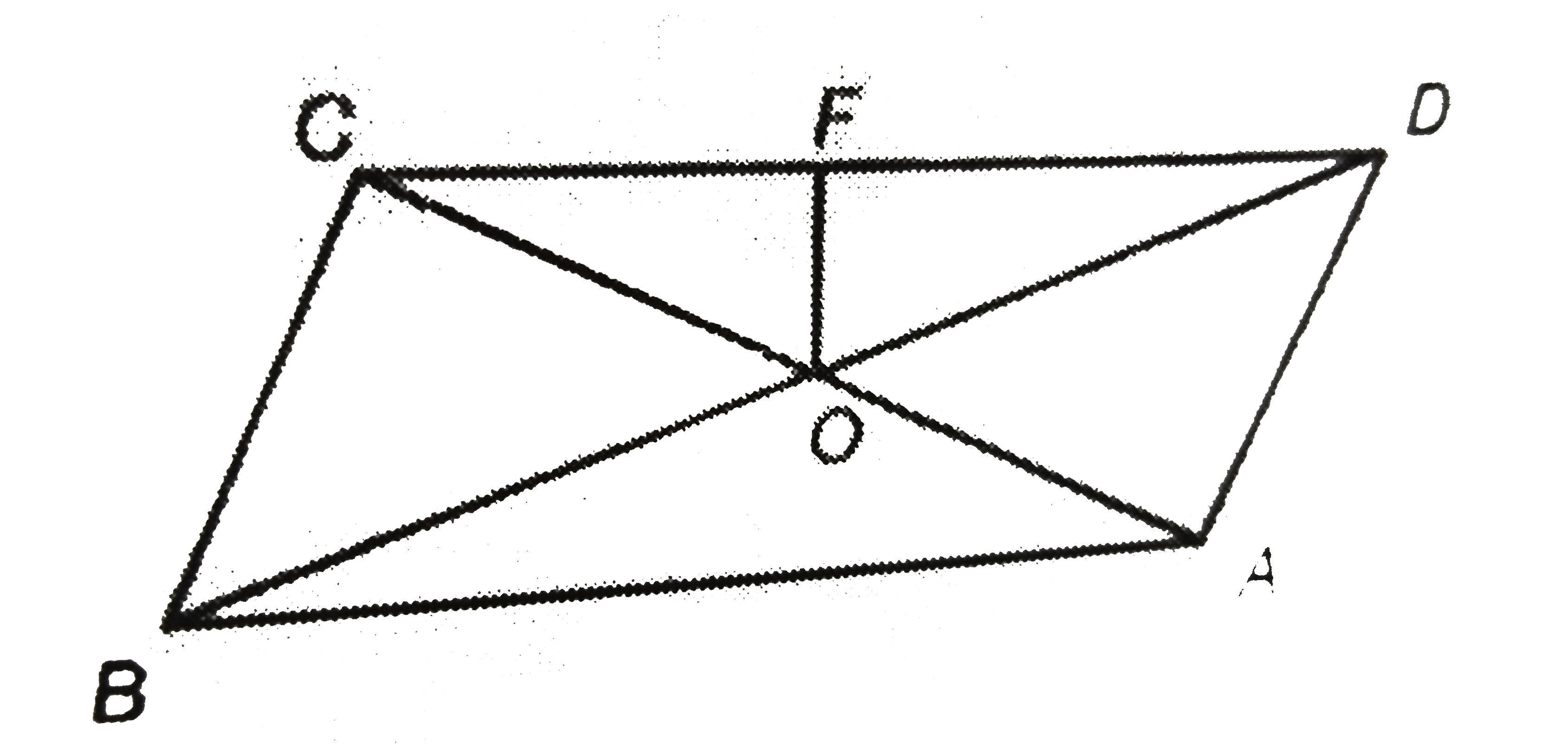
View SolutionFind the length of the sides of a given parallogram, if the perimeter of the paralleloram is 24 cm, the length of perpendicular OF=3cm, OB=5 cm and OC=`sqrt(18)cm`.
View SolutionIn the figure given below, OD=OC=OB. Find `angle DCB`.
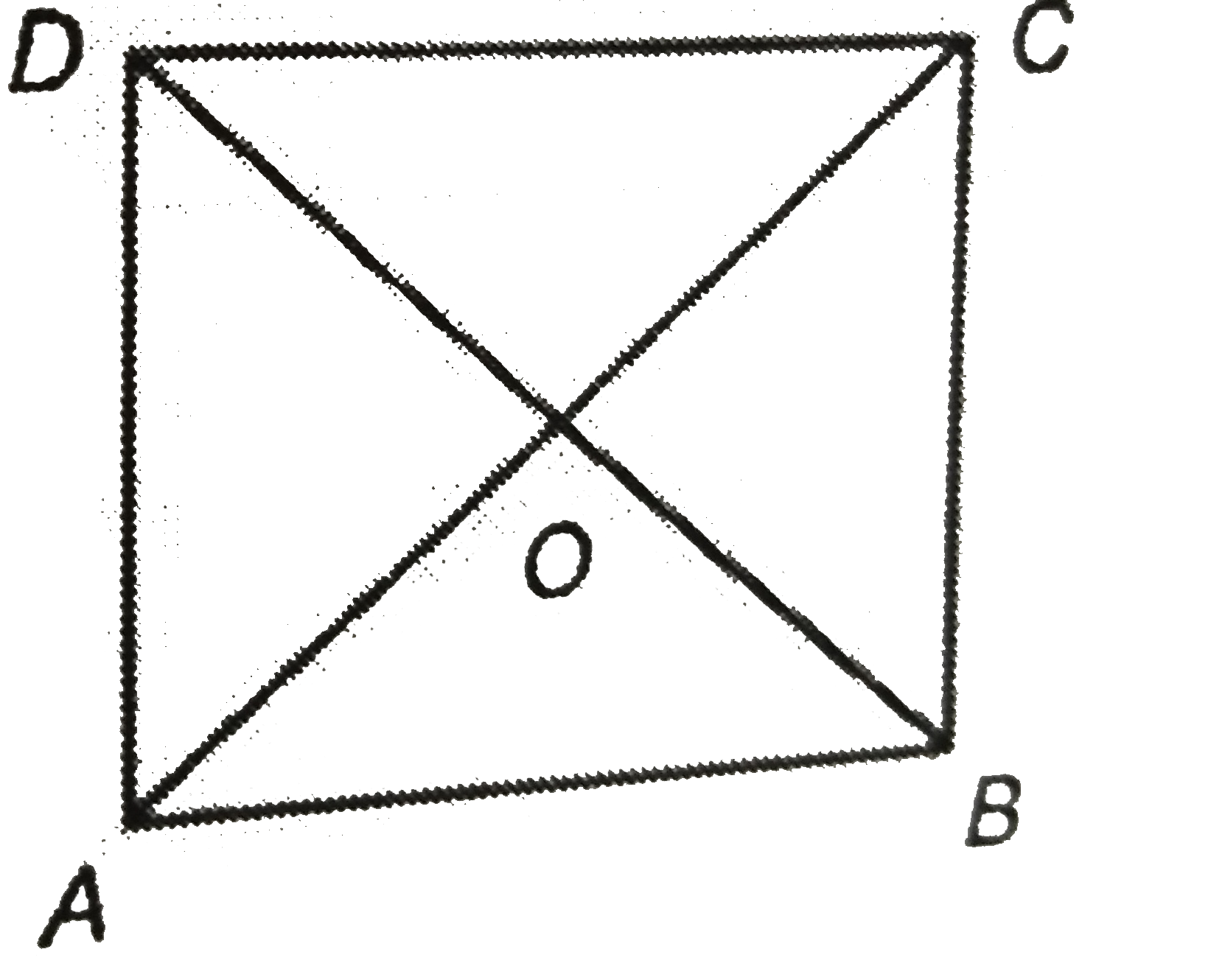
View SolutionIf the sum of the lengths of two diagonals of the given square ABCD is 24 cm, then find the side of the square and the magnitude of AO + OB.
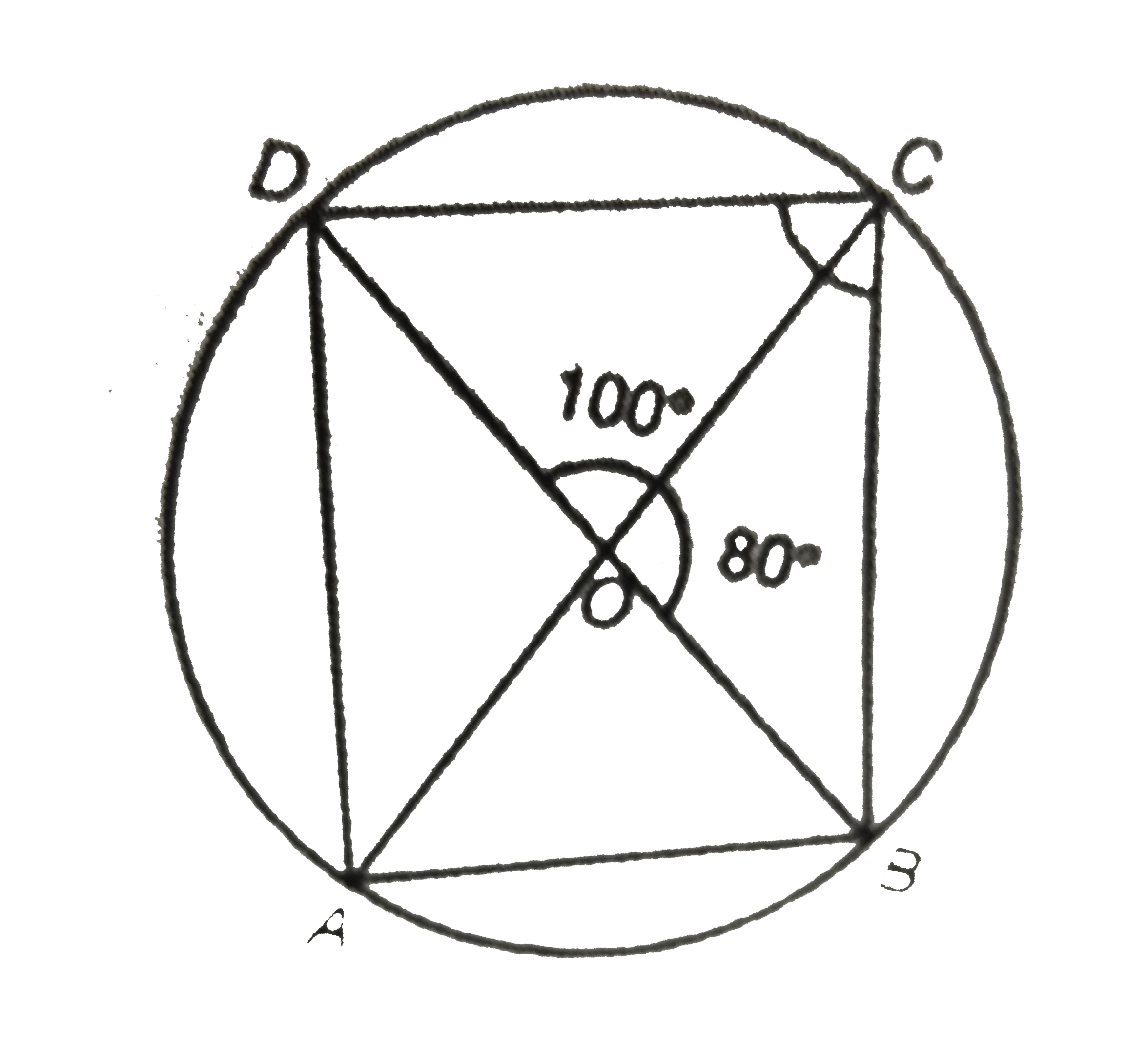
View SolutionIn the following figure, O is the center of the circle. If `x=40^(@)` and `x:y=4:3`, find the value of z.

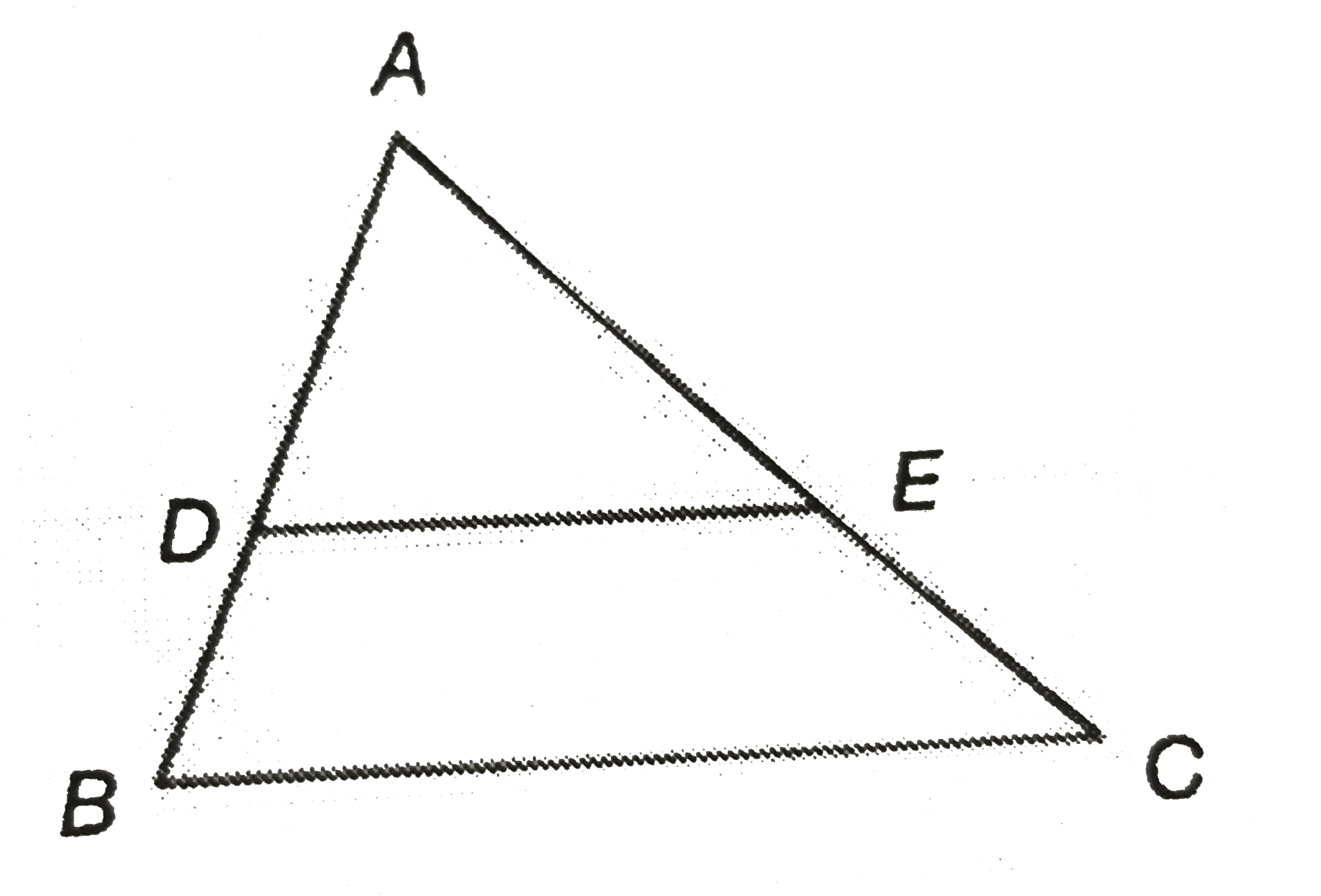
View SolutionIn the following figure, AD=5.6 cm, AE=`(x+1)cm, AB=8.4cm` and `EC=(x-1)cm`, find AC. Given that `DE|| BC`.
View SolutionABCD and BFDC are cyclic quadrilaterals. `bar(CD)` is produced to E. If `angleBCE=45^(@)`, then find `angleBFD`.

View SolutionFind `angleDBA, angleDAB` and `angleAED` in the following figure, where ABCDE is a semi-circle.

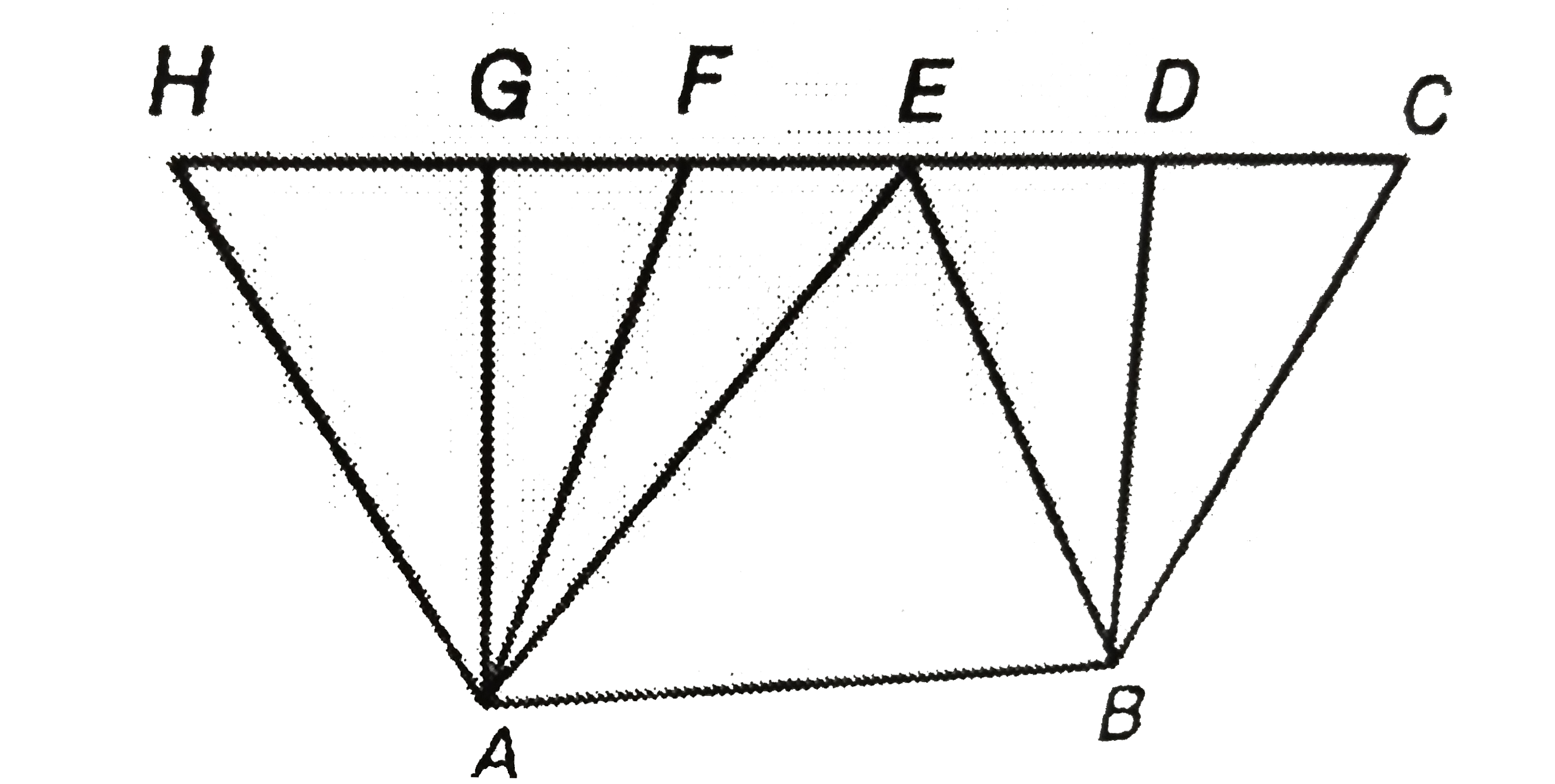
View SolutionIn the following figure, ABDG is a rectangle with AB=10 cm and AG=6 cm. Find the areas of parallelogram ABCF and ABEH. Also find the area of `triangleAEB`.
View SolutionIn the following figure, `bar(BD)` is produced to E. If `bar(AD)` is the angle bisector of `angleA`, then find the `angleBCD`.

View Solution
SHORT ANSWER TYPE QUESTIONS questions and complete solutions for chapter GEOMETRY of PEARSON IIT JEE FOUNDATION of Class 9