Complete Solutions to EXERCISE of chapter ਚਤੁਰਭੁਜ of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | ਚਤੁਰਭੁਜ |
| PSEB (PUNJABI MEDIUM) | EXERCISE |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
ਇੱਕ ਚਤੁਰਭੁਜ ਦੇ ਕੋਣ 3 : 5 : 9 : 13 ਦੇ ਅਨੁਪਾਤ ਵਿੱਚ ਹਨ। ਇਸ ਚਤੁਰਭੁਜ ਦੇ ਸਾਰੇ ਕੋਣ ਪਤਾ ਕਰੋ।
View Solutionਜੇ ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਬਰਾਬਰ ਹੋਣ , ਤਾਂ ਦਰਸਾਉ ਕਿ ਇਹ ਇੱਕ ਆਇਤ ਹੈ।
View Solutionਦਰਸਾਉ ਕਿ ਜੇ ਇੱਕ ਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਣ ਆਪਸ ਵਿੱਚ, ਸਮਕੋਣ 'ਤੇ ਸਮਦੁਭਾਜਿਤ ਕਰਨ,ਤਾਂ ਉਹ ਇਕ ਸਮਚਤੁਰਭੁਜ ਹੁੰਦੀ ਹੈ।
View Solutionਦਰਸਾਉ ਕਿ ਇੱਕ ਵਰਗ ਦੇ ਵਿਕਰਣ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਆਪਸ ਵਿੱਚ ਸਮਕੋਣ 'ਤੇ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ।
View Solutionਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦਾ ਵਿਕਰਣ AC ਕੋਣ A ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ।(ਦੇਖੋ ਚਿੱਤਰ 8.19)। ਦਰਸਾਉ ਕਿ (1) ਇਹ `angle C` ਨੂੰ ਵੀ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ। (2) ABCD ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ।

View SolutionABCD ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ।ਦਰਸਾਉ ਕਿ ਵਿਕਰਣ AC ਕੋਣ A ਅਤੇ C ਦੋਵਾਂ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ ਅਤੇ ਵਿਕਰਣ BD ਕੋਣਾਂ B ਅਤੇ D ਦੋਵਾਂ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ।
View SolutionABCD ਇੱਕ ਆਇਤ ਹੈ, ਜਿਸ ਵਿੱਚ ਵਿਕਰਣ AC ਦੋਵੇਂ ਕੋਣਾਂ A ਅਤੇ C ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ। ਦਰਸਾਉ ਕਿ (i) ABCD ਇੱਕ ਵਰਗ ਹੈ। (ii) ਵਿਕਰਣ BD ਦੋਵੇਂ ਕੋਣ B ਅਤੇ D ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦਾ ਹੈ।
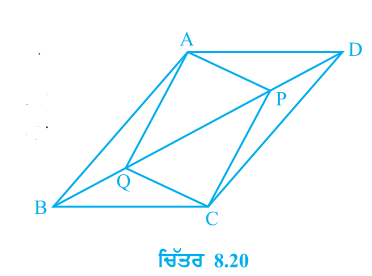
View Solutionਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ BD 'ਤੇ ਦੋ ਬਿੰਦੂ P ਅਤੇ Q ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹਨ ਕਿ DP=BQ ਹੈ (ਦੇਖੋ ਆਕ੍ਰਿਤੀ 8.20)। ਦਰਸਾਉ ਕਿ `triangle APD cong triangle CQB`
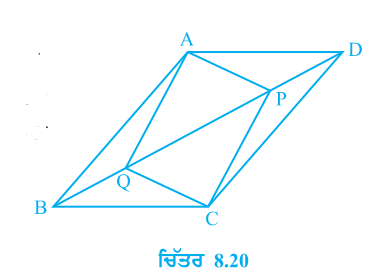
View Solutionਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ BD 'ਤੇ ਦੋ ਬਿੰਦੂ P ਅਤੇ Q ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹਨ ਕਿ DP=BQ ਹੈ (ਦੇਖੋ ਆਕ੍ਰਿਤੀ 8.20)। ਦਰਸਾਉ ਕਿ AP = CQ
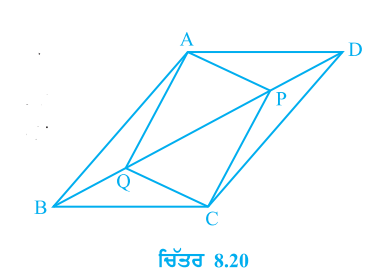
View Solutionਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ BD 'ਤੇ ਦੋ ਬਿੰਦੂ P ਅਤੇ Q ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹਨ ਕਿ DP=BQ ਹੈ (ਦੇਖੋ ਆਕ੍ਰਿਤੀ 8.20)। ਦਰਸਾਉ ਕਿ `triangle AQB cong triangle CPD`
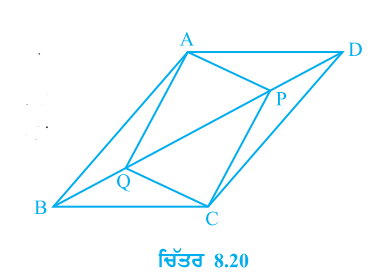
View Solutionਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ BD 'ਤੇ ਦੋ ਬਿੰਦੂ P ਅਤੇ Q ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹਨ ਕਿ DP=BQ ਹੈ (ਦੇਖੋ ਆਕ੍ਰਿਤੀ 8.20)। ਦਰਸਾਉ ਕਿ AQ = CP
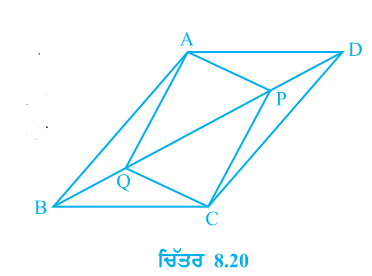
View Solutionਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ BD 'ਤੇ ਦੋ ਬਿੰਦੂ P ਅਤੇ Q ਇਸ ਪ੍ਰਕਾਰ ਸਥਿਤ ਹਨ ਕਿ DP=BQ ਹੈ (ਦੇਖੋ ਆਕ੍ਰਿਤੀ 8.20)। ਦਰਸਾਉ ਕਿ APCQ ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ।
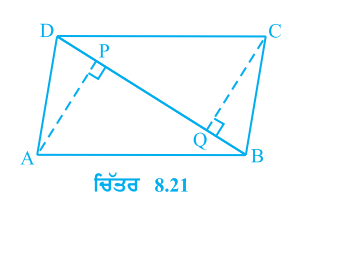
View SolutionABCD ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ਅਤੇ AP ਅਤੇ CQ ਸਿਖਰਾਂ A ਅਤੇ C ਤੋਂ ਵਿਕਰਣ BD 'ਤੇ ਕ੍ਰਮਵਾਰ ਲੰਬ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ 8.21)। ਦਰਸਾਉ ਕਿ (i) `triangle APB cong triangle CQD` (ii) AP = CQ
View Solution`triangle ABC` ਅਤੇ `triangle DEF` ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- ਚਤਰੁਭੁਜ ABED ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ।
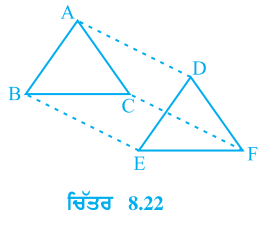
View Solution`triangle ABC` ਅਤੇ `triangle DEF` ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- ਚਤਰੁਭੁਜ BEFC ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ।
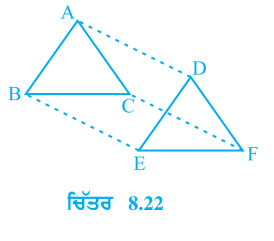
View Solution`triangle ABC` ਅਤੇ `triangle DEF` ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- AD || CF ਅਤੇ AD = CF ਹੈ।
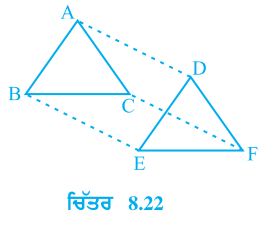
View Solution`triangle ABC` ਅਤੇ `triangle DEF` ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- ਚਤਰੁਭੁਜ ACFD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ।
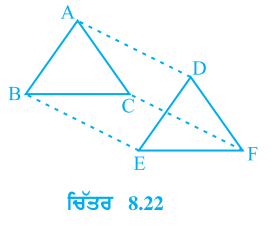
View Solution`triangle ABC` ਅਤੇ `triangle DEF` ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- AC = DF ਹੈ।
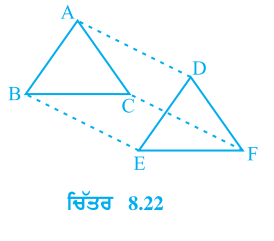
View Solution`triangle ABC` ਅਤੇ `triangle DEF` ਵਿੱਚ,AB = DE, AB || DE, BC = EF ਅਤੇ BC || EF ਹੈ। ਸਿਖਰਾਂ A,B ਅਤੇ C ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਿਖਰਾਂ D,E ਅਤੇ F ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ 8.22)। ਦਰਸਾਉ ਕਿ:- `triangle ABC cong triangle DEF` ਹੈ।
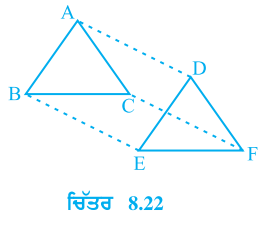
View SolutionABCD ਇੱਕ ਸਮਲੰਬ ਹੈ, ਜਿਸ ਵਿੱਚ AB || CD ਅਤੇ AD = BC ਹੈ। (ਦੇਖੋ ਚਿੱਤਰ 8.23)। ਦਰਸਾਉ ਕਿ `angleA = angle B` [ਸੰਕੇਤ:-AB ਨੂੰ ਵਧਾਉ ਅਤੇ C ਤੋਂ ਹੋ ਕੇ DA ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਜੋ ਵਧੀ ਹੋਈ ਭੁਜਾ AB ਨੂੰ E 'ਤੇ ਕੱਟੇ।]
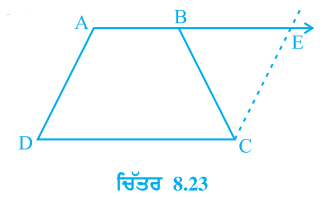
View SolutionABCD ਇੱਕ ਸਮਲੰਬ ਹੈ, ਜਿਸ ਵਿੱਚ AB || CD ਅਤੇ AD = BC ਹੈ। (ਦੇਖੋ ਚਿੱਤਰ 8.23)। ਦਰਸਾਉ ਕਿ `angleC = angle D` [ਸੰਕੇਤ:-AB ਨੂੰ ਵਧਾਉ ਅਤੇ C ਤੋਂ ਹੋ ਕੇ DA ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਜੋ ਵਧੀ ਹੋਈ ਭੁਜਾ AB ਨੂੰ E 'ਤੇ ਕੱਟੇ।]

View SolutionABCD ਇੱਕ ਸਮਲੰਬ ਹੈ, ਜਿਸ ਵਿੱਚ AB || CD ਅਤੇ AD = BC ਹੈ। (ਦੇਖੋ ਚਿੱਤਰ 8.23)। ਦਰਸਾਉ ਕਿ `triangle ABC cong triangle BAD` [ਸੰਕੇਤ:-AB ਨੂੰ ਵਧਾਉ ਅਤੇ C ਤੋਂ ਹੋ ਕੇ DA ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਜੋ ਵਧੀ ਹੋਈ ਭੁਜਾ AB ਨੂੰ E 'ਤੇ ਕੱਟੇ।]

View SolutionABCD ਇੱਕ ਸਮਲੰਬ ਹੈ, ਜਿਸ ਵਿੱਚ AB || CD ਅਤੇ AD = BC ਹੈ। (ਦੇਖੋ ਚਿੱਤਰ 8.23)। ਦਰਸਾਉ ਕਿ ਵਿਰਕਣ AC =ਵਿਰਕਣ BD ਹੈ। [ਸੰਕੇਤ:-AB ਨੂੰ ਵਧਾਉ ਅਤੇ C ਤੋਂ ਹੋ ਕੇ DA ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਜੋ ਵਧੀ ਹੋਈ ਭੁਜਾ AB ਨੂੰ E 'ਤੇ ਕੱਟੇ।]

View SolutionABCD ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿਚ P,Q,R ਅਤੇ S ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ(ਦੇਖੋ ਚਿੱਤਰ 8.29)। ਉਸਦਾ ਇਕ ਵਿਕਰਣ ਹੈ। ਦਰਸਾਉ ਕਿ SR || AC ਅਤੇ `SR =1/2 AC` ਹੈ।
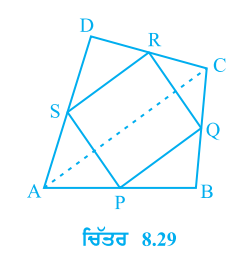
View SolutionABCD ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿਚ P,Q,R ਅਤੇ S ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ(ਦੇਖੋ ਚਿੱਤਰ 8.29)। ਉਸਦਾ ਇਕ ਵਿਕਰਣ ਹੈ। ਦਰਸਾਉ ਕਿ PQ = SR ਹੈ।
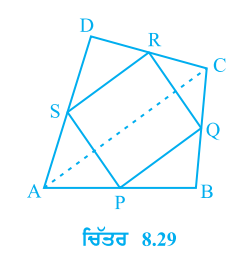
View SolutionABCD ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ ਜਿਸ ਵਿਚ P,Q,R ਅਤੇ S ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ(ਦੇਖੋ ਚਿੱਤਰ 8.29)। ਉਸਦਾ ਇਕ ਵਿਕਰਣ ਹੈ। ਦਰਸਾਉ ਕਿ PQRS ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ।

View SolutionABCD ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ ਅਤੇ P, Q, R ਅਤੇ S ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ। ਦਰਸਾਉ ਕਿ ਚਤੁਰਭੁਜ PQRS ਇੱਕ ਆਇਤ ਹੈ।
View SolutionABCD ਇੱਕ ਆਇਤ ਹੈ, ਜਿਸ ਵਿਚ P, Q, R ਅਤੇ S ਅਤੇ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ। ਦਰਸਾਉ ਕਿ ਚਤੁਰਭੁਜ PQRS ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ।
View SolutionABCD ਇੱਕ ਸਮਲੰਬ ਚਤੁਰਭੁਜ ਹੈ, ਜਿਸ ਵਿੱਚ AB || DC ਹੈ। ਨਾਲ ਹੀ, BD ਇਕ ਵਿਕਰਣ ਹੈ ਅਤੇ E ਭੁਜਾ AD ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ। E ਤੋਂ ਹੋ ਕੇ ਇਕ ਰੇਖਾ AB ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਹੈ, ਜੋ BC ਨੂੰ F 'ਤੇ ਕੱਟਦੀ ਹੈ।(ਦੇਖੋ ਚਿੱਤਰ 8.30)। ਦਰਸਾਉ ਕਿ F ਭੁਜਾ BC ਦਾ ਮੱਧ- ਬਿੰਦੂ ਹੈ।

View Solutionਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਵਿਚ E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB ਅਤੇ CD ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ 8.31)। ਦਰਸਾਉ ਕਿ ਰੇਖਾ ਖੰਡ AF ਅਤੇ EC ਵਿਕਰਣ BD ਨੂੰ ਤਿੰਨ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿਚ ਵੰਡਦਾ ਹੈ।
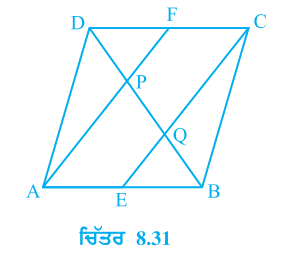
View Solutionਦਰਸਾਉ ਕਿ ਕਿਸੇ ਚਤੁਰਭੁਜ ਦੀਆਂ ਸਨਮੁੱਖ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾ ਖੰਡ ਇਕ ਦੂਜੇ ਨੂੰ ਸਮਦੁਭਾਜਿਤ ਕਰਦੇ ਹਨ।
View SolutionABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ। ਕਰਣ AB ਦੇ ਮੱਧ ਬਿੰਦੂ M ਤੋਂ ਹੋ ਕੇ BC ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਰੇਖਾ AC ਨੂੰ D 'ਤੇ ਕੱਟਦੀ ਹੈ। ਦਰਸਾਉ ਕਿ :-D ਭੁਜਾ AC ਦਾ ਮੱਧ-ਬਿੰਦੂ ਹੈ।
View SolutionABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ। ਕਰਣ AB ਦੇ ਮੱਧ ਬਿੰਦੂ M ਤੋਂ ਹੋ ਕੇ BC ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਰੇਖਾ AC ਨੂੰ D 'ਤੇ ਕੱਟਦੀ ਹੈ। ਦਰਸਾਉ ਕਿ :- `MD bot AC` ਹੈ।
View SolutionABC ਇੱਕ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ C ਸਮਕੋਣ ਹੈ। ਕਰਣ AB ਦੇ ਮੱਧ ਬਿੰਦੂ M ਤੋਂ ਹੋ ਕੇ BC ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਰੇਖਾ AC ਨੂੰ D 'ਤੇ ਕੱਟਦੀ ਹੈ। ਦਰਸਾਉ ਕਿ :- `CM = MA =1/2 AB` ਹੈ।
View Solution
EXERCISE questions and complete solutions for chapter ਚਤੁਰਭੁਜ of PSEB (PUNJABI MEDIUM) of Class 9