Complete Solutions to EXERCISE of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| PSEB | EXERCISE |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
In quadrilateral ACBD, AC = AD and AB bisects `angle A` (see Fig. 7.16). Show that `triangle ABC cong triangle ABD`. What can you say about BC and BD?
View SolutionABCD is a quadrilateral in which AD = BC and `angle DAB =angle CBA` (see Fig. 7.17). Prove that (i) `triangle ABD cong triangle BAC` (ii) BD = AC (iii) `angle ABD = angle BAC`.
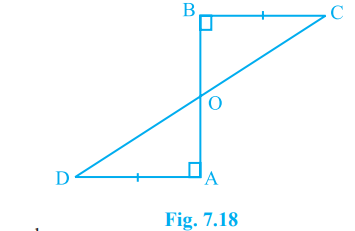
View SolutionAD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
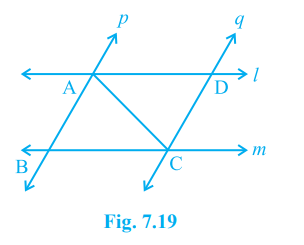
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that `triangle ABC cong triangle CDA`
View SolutionLine l is the bisector of an angle `angle A` and B is any point on l. BP and BQ are perpendiculars from B to the arms of `angle A` (see Fig. 7.20). Show that: (i) `triangle APB cong triangle AQB` (ii) BP = BQ or B is equidistant from the arms of `angle A`.

View SolutionIn Fig. 7.21, AC = AE, AB = AD and `angle BAD = angle EAC`. Show that BC =DE.

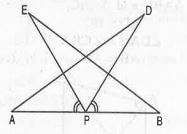
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AB such that `angleBAD = angleABE` and `angleEPA = angleDPB`. Show that AD=BE.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.)

Show that : `CM=1/2AB`.
View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of `angleB` and `angleC` intersect each other at O. Join A to O show that : OB=OC.
View SolutionIn `DeltaABC`, AD is the perpendicular bisector of BC (See Fig.
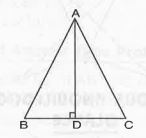 ). Show that `DeltaABC` is an isosceles triangle in which AB = AC.
). Show that `DeltaABC` is an isosceles triangle in which AB = AC.
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.
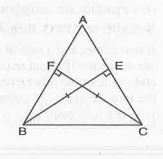 ). Show that these altitudes are equal.
). Show that these altitudes are equal.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (See Fig.
 ). Show that `DeltaABE ~= DeltaACF`.
). Show that `DeltaABE ~= DeltaACF`.
View SolutionABC and DBC are two isosceles triangles on the same base BC (See Fig.
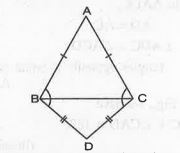 ). Show that `angleABD = angleACD`.
). Show that `angleABD = angleACD`.
View Solution`DeltaABC` is an isoscelestriangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that `angleBCD` is a right angle (see Fig.
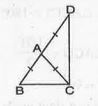 ).
).
View SolutionABC is a right angled triangle in which `angle A = 90^@` and AB = AC. Find `angle B` and `angle C`.
View SolutionShow that the angles of an equilateral triangle are`60^@` each.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
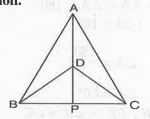 ).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
 ).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
).If AD is extended to intersect BC at P, show that `DeltaABD ~= DeltaACD`.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
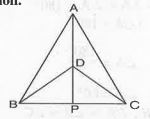 ).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.
).If AD is extended to intersect BC at P, show that AP bisects `angleA` as well as `angleD`.
View Solution`DeltaABC` and `DeltaDBC` are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
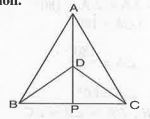 ).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.
).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:- AD bisects BC
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:- AD bisects `angle A`.
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of `DeltaPQR` (See Fig
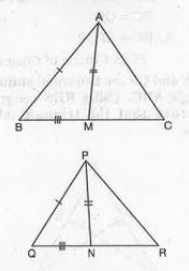 ). Show that : `DeltaABM ~= DeltaPQN`.
). Show that : `DeltaABM ~= DeltaPQN`.
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of `DeltaPQR` (See Fig
 ). Show that : `DeltaABC ~=DeltaPQR`.
). Show that : `DeltaABC ~=DeltaPQR`.
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionABC is an isosceles triangle with AB = AC. Draw `AP bot BC` to show that `angle B = angle C`.
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionIn Fig.
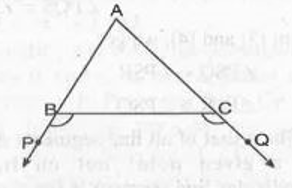 , sides AB and AC of `DeltaABC` are extended to points P and Q respectively. Also `anglePBC < angleQCB`. Show that `AC > AB`.
, sides AB and AC of `DeltaABC` are extended to points P and Q respectively. Also `anglePBC < angleQCB`. Show that `AC > AB`.
View SolutionIn Fig. 7.49, `angle B < angle A` and `angle C < angle D`. Show that AD < BC.
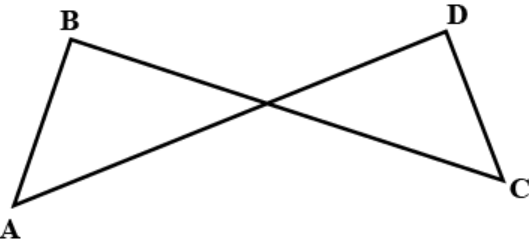
View SolutionAB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that `angle A > angle C` and `angle B > angle D`.
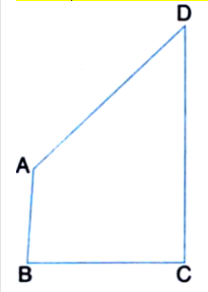
View SolutionIn Fig 7.51, PR > PQ and PS bisects `angle QPR`. Prove that `angle PSR > angle PSQ`.
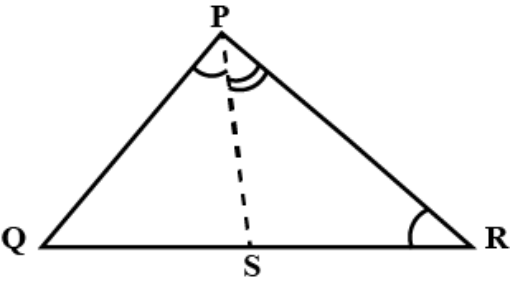
View SolutionShow that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
View SolutionABC is a triangle. Locate a point in the interior of `DeltaABC` which is equidistant from all the vertices of `DeltaABC`.
View SolutionIn a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
View SolutionIn a huge park, people are concentrated at three points
A : where there are different slides and swings for children. B : near which a man-made lake is situated. C : which is near to a large parking and exit. Where should an icecream parlour be set up so that maximum number of persons can approach it ?
View SolutionComplete the hexagonal rangoli and the star Rangolies (see Figs.
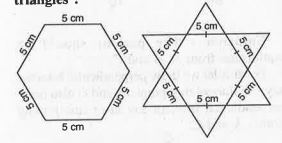 ) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?
) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles ?
View Solution
EXERCISE questions and complete solutions for chapter TRIANGLES of PSEB of Class 9