Complete Solutions to EXAMPLE of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| PSEB | EXAMPLE |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Show that each angle of a rectangle is a right angle.
01:52View SolutionThe diagonals of a rhombus are perpendicular to each other .
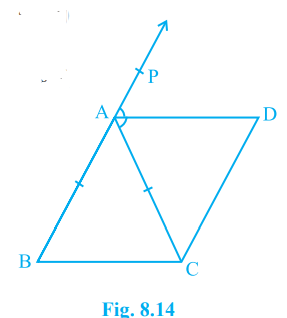
04:12View SolutionABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || AB (see Fig. 8.14). Show that (i) `angle DAC = angle BCA` and (ii) ABCD is a parallelogram.
 10:44View Solution
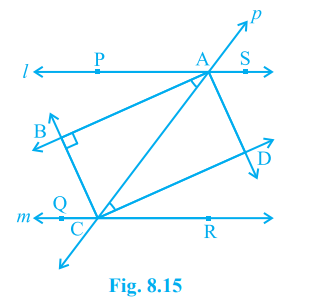
10:44View SolutionTwo parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
 09:21View Solution
09:21View SolutionThe bisectors of angles of a parallelogram from a :
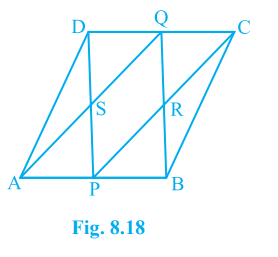
05:07View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: APCQ is a parallelogram.
 04:20View Solution
04:20View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: APCQ is a parallelogram.
 04:20View Solution
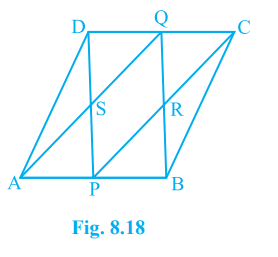
04:20View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: DQBP is a parallelogram.
 04:29View Solution
04:29View SolutionIn `Delta ABC`, D, E and F are respectively the mid-points of sides AB, BC and CA . Show that `Delta ABC is divided into four congruent triangles by joining D, E and F.
06:46View Solutionl, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Fig. 8.28). Show that l, m and n cut off equal intercepts DE and EF on q also.
 07:01View Solution
07:01View Solution
EXAMPLE questions and complete solutions for chapter QUADRILATERALS of PSEB of Class 9
