Complete Solutions to EXERCISE of chapter QUADRILATERALS of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | QUADRILATERALS |
| PSEB | EXERCISE |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
02:02View SolutionIf the diagonals of a parallelogram are perpendicular, then it is a rhombus.
04:16View SolutionIf diagonals of a quadrilateral bisect each other at right angles, then it is a :
01:33View SolutionWhich of the following statements are True or False :
If the diaonals of a quadilateral are equal and bisect each other at right angles then the quadrilateral is a square.01:42View SolutionWhich of the following statements are True or False :
If the diaonals of a quadilateral are equal and bisect each other at right angles then the quadrilateral is a square.01:42View SolutionDiagonal AC of a parallelogram ABCD bisects `angle A` (see Fig. 8.19). Show that (i) it bisects `angle C` also, (ii) ABCD is a rhombus.
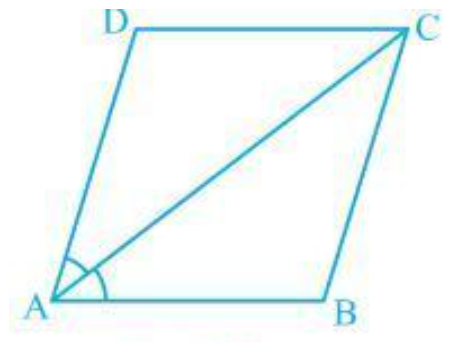 09:01View Solution
09:01View SolutionABCD is a rhombus. Show that the diagonal AC bisects `/_A` as well as `/_C` and diagonal BD bisects `/_B` as well as `/_D`.
06:29View SolutionABCD is a rectangle in which diagonal AC bisects `/_A as well as `/_C`. Show that Diagonal BD bisects both `/_B` as well as `/_D`.
06:45View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that `AQ=CP`.04:05View Solution
) Show that `AQ=CP`.04:05View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that `AQ=CP`.04:05View Solution
) Show that `AQ=CP`.04:05View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that `AQ=CP`.04:05View Solution
) Show that `AQ=CP`.04:05View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that `AQ=CP`.04:05View Solution
) Show that `AQ=CP`.04:05View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.
 ) Show that APCQ is a parallelogram.02:36View Solution
) Show that APCQ is a parallelogram.02:36View SolutionABCD is a parallelogram and AP and CQ are the perpendiculars from vertices A and C on its diagonal BD (See fig.) Show that `Delta APB ~= Delta CQD`.
02:27View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that quadrilateral ABED is a parallelogram.02:47View Solution
Show that quadrilateral ABED is a parallelogram.02:47View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, `BC = EF` and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that quadrilateral BEFC is a parallelogram.01:13View Solution
Show that quadrilateral BEFC is a parallelogram.01:13View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
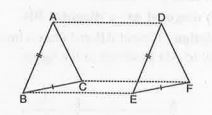 Show that `AD ||CF` and AD=CF.04:52View Solution
Show that `AD ||CF` and AD=CF.04:52View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
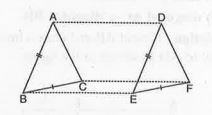 Show that quadrilateral ACFD is a parallelogram.05:04View Solution
Show that quadrilateral ACFD is a parallelogram.05:04View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
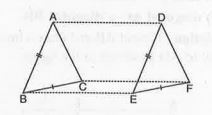 Show that AC=DF.04:51View Solution
Show that AC=DF.04:51View SolutionIn `Delta ABC` and `Delta DEF` , AB = DE, `AB|| DE`, BC = EF and `BC|| EF`. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
 Show that `DeltaABC ~= DeltaDEF`.01:47View Solution
Show that `DeltaABC ~= DeltaDEF`.01:47View SolutionABCD is a trapezium in which `AB||CD` and AD = BC (See Fig.)
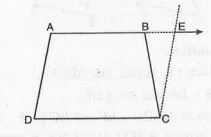 Show that `/_A = /_B`.08:24View Solution
Show that `/_A = /_B`.08:24View SolutionABCD is a trapezium in which `AB||CD` and AD = BC (See Fig.)
 Show that `/_C = /_D`.03:39View Solution
Show that `/_C = /_D`.03:39View SolutionABCD is a trapezium in which `AB||CD` and AD = BC (See Fig.)
 Show that `Delta ABC ~= Delta BAD`.05:04View Solution
Show that `Delta ABC ~= Delta BAD`.05:04View SolutionABCD is a trapezium in which `AB||CD` and AD = BC (See Fig.)
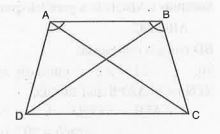 Show that diagonal AC = diagonal BD.02:57View Solution
Show that diagonal AC = diagonal BD.02:57View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
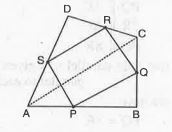 AC is a diagonal Show that `SR II AC and SR = 1/2 AC`.05:26View Solution
AC is a diagonal Show that `SR II AC and SR = 1/2 AC`.05:26View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.)
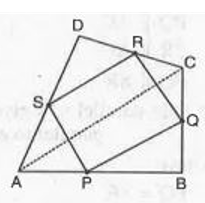 AC is a diagonal Show that PQ = SR.02:37View Solution
AC is a diagonal Show that PQ = SR.02:37View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.)
 AC is a diagonal Show that PQRS is a parallelogram.05:35View Solution
AC is a diagonal Show that PQRS is a parallelogram.05:35View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
10:11View SolutionABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
06:19View SolutionABCD is a trapezium, in which `AB II DC`, BD is a diagonal and E is the mid-point of AD. A line is drawn through E, parallel to AB intersecting BC at F (See Fig.)
 Show that F is the mid-point of BC.02:57View Solution
Show that F is the mid-point of BC.02:57View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (See Fig)
 . Show that the line segments AF and EC trisect the diagonal BD.04:10View Solution
. Show that the line segments AF and EC trisect the diagonal BD.04:10View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
03:28View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
01:14View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that `MD _|_ AC`.
01:31View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that CM = MA = `1/2 AB` .
07:24View Solution
EXERCISE questions and complete solutions for chapter QUADRILATERALS of PSEB of Class 9
