Complete Solutions to प्रश्नावली 24.2 of chapter समान्तर चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समान्तर चतुर्भुज |
| S CHAND | प्रश्नावली 24.2 |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
यदि एक समचतुर्भुज के विकर्ण 9 सेमी और 12 सेमी है, तो इसके भुजाओं को ज्ञात करें।
06:19View Solution`Delta ABC` में, `/_ A = 40^(@), /_B = 80^(@), /_ C = 60^(@)` तो इस त्रिभुज की भुजाओं के मध्य-बिंदुओं को मिलाने से बने त्रिभुज के कोणों का माप ज्ञात करें।
04:14View Solutionएक त्रिभुज में P,Q तथा R क्रमशः भुजाएँ BC,CA और AB के मध्य-बिंदु हैं। यदि AC=16 सेमी BC = 20 सेमी औरAB = 24 सेमी , तो चतुर्भुज ARPQ का परिमाप ज्ञात करें।
04:53View SolutionABC एक त्रिभुज हैं और A,B तथा C से होकर क्रमशः BC,CA तथा AB के समांतर रेखाएँ खींची गई हैं जो P,Q तथा R पर प्रतिच्छेदित होती है। सिद्ध करें कि `Delta PQR` का परिमाप, `Delta ABC` के परिमाप का दुगुना है।
06:41View Solution`Delta ABC` में,माध्यिका AD को P तक इस प्रकार बढ़ाया गया है। कि AD = DP, सिद्ध करें कि ABPC एक समांतर चतरभुज है।
01:37View Solution`Delta ABC` में, E तथा F क्रमशः AC तथा AB के मध्य-बिंदु है। BC पर डाला गया शीर्षलांब AP, EF को Q पर प्रतिच्छेदित करता है। सिद्ध करें कि `AQ = QP`
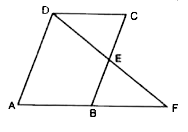
03:19View SolutionABCD एक समांतर चतुर्भुईंज है और E भुजा BC का मध्य-बिंदु है। यदि DE और AB को बढ़ाने पर वे F पर मिलते हैं, तो सिद्ध करें कि AF = 2AB
 03:08View Solution
03:08View Solutionदो बिन्दु M एवं N क्रमश: `Detla ABC` की भुजाओं AB एवं AC पर इस प्रकार स्थित है कि `AM = (1)/(4) AB` तथा `AN = (1)/(4) AC` है। सिद्ध करें कि `MN = (1)/(4) BC` होगा।
02:26View Solutionएक त्रिभुज `Delta ABC` में, BM तथा CN क्रमशः B और C से, A से होकर जाने वाली किसी रेखा पर खींचे गए लंब हैं । यदि L,BC का मध्य-बिंदु हो, तो सिद्ध करें कि ML = NL
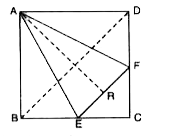
02:08View SolutionABCD एक वर्ग है और EF,BD के समांतर है। यदि R,EF का मध्य-बिंदु है, तो सिद्ध करें कि
(i) BE = DF (ii) AR, `/_ BAD` को समद्विभाजित करता है। (III) यदि AR को बढ़ाया जाय , तो यह C से होकर जाएगा।
 09:22View Solution
09:22View Solutionसिद्ध करें कि समांतर चतुर्भुज के सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाली सरल रेखाएँ, समांतर भुजाओं के दूसरे युग्मों के समांतर होते हैं।
02:40View SolutionABCD एक समांतर चतुर्भुज है। X,AD का मध्य-बिंदु है और Y,BC का मध्य-बिंदु है। सिद्ध करें कि XY और BD एक दूसरे को समद्विभाजित करते हैं।
03:07View SolutionABCD एक पतंगाकार आकृति है, जिसमें AB=AD और BC = CD सिद्ध करें कि भुजाओं के मध्य-बिंदुओं को क्रमागत मिलाने से बनी आकृति एक आयत है।
06:09View SolutionABCD एक समचतुर्भुज है। RABS एक सरल रेखा इस प्रकार है कि RA=AB=BS सिद्ध करें कि RD और SC को बढ़ाने पर वे समकोण पर मिलते हैं।
04:09View Solutionआकृति में ABCD औरPQRC आयत हैं और Q,AC का मध्य-बिंदु है। सिद्ध करें कि (i) `DP =PC` (ii) `PR = ( 1)/( 2) AC`
 09:36View Solution
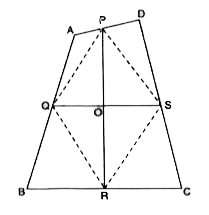
09:36View Solutionआकृति में,P,Q,R तथा S क्रमशः चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं। सिद्ध करें कि O,PR औरQS दोनों का मध्य-बिंदु है।
 05:11View Solution
05:11View Solutionआकृति में `BE _|_ AC` , AD,A से BC पर खींची गई कोई रेखा है, जो BE को H पर प्रतिच्छेद करती है। P,Q और R क्रमशः AH,AB और BC के मध्य-बिंदु हैं। सिद्ध करें कि `/_ PQR = 90^(@)`
 04:21View Solution
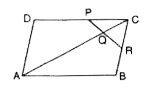
04:21View Solutionआकृति में, ABCD एक समांतर चतुर्भुज है, जिसमें [.DC का मध्य-बिंदु है और Q.AC पर एक बिंदु इस प्रकार है कि `CQ = ( 1)/( 4) AC `. यदि PQ को बढ़ाने पर वह BC से R पर मिलती है , तो सिद्ध करें कि R,BC का मध्य-बिंदु है।
 04:59View Solution
04:59View SolutionABCD एक समांतर चतुर्भुज है। E और F क्रमशः AB और CD के मध्य-बिंदु हैं। GH कोई रेखा है जो AD,EF और BC को क्रमशः G,P और H पर प्रतिच्छेद होते हैं। सिद्ध करें कि `GP = PH`.
05:25View SolutionPQRS एक समचतुर्भुज है। विकर्ण PR और QS,O पर प्रतिच्छेदित होते हैं। सिद्ध करें कि इस तरह से बने सभी चार त्रिभुजें सर्वांगसम होती है।
06:48View SolutionABCD एक समचतुर्भुज है। P,Q,R तथा S क्रमशः AB,BC,CD और DA के मध्य-बिंदु हैं। सिद्ध करें कि PQRS एक आयत है।
05:46View SolutionABCD एक समांतर चतुर्भुज है। AD को E तक इस प्रकार बढ़ाया गया है कि DE = DC और EC के बढ़े हुए भाग AB के बढ़े हुए भाग F को पर प्रतिच्छेद करते हैं । सिद्ध करें कि BF=BC
04:04View Solution
प्रश्नावली 24.2 questions and complete solutions for chapter समान्तर चतुर्भुज of S CHAND of Class 9