Complete Solutions to साधित उदाहरण of chapter समान्तर चतुर्भुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समान्तर चतुर्भुज |
| S CHAND | साधित उदाहरण |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
आकृति में ABCD एक समान्तर चतुर्भुज है, तो x तथा y के मान की गणना करें।
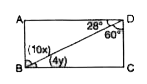
View Solutionसिद्ध करें कि किसी समान्तर चतुर्भुज के दो क्रमागत कोणों का योग `180^(@)` होगा है।

View Solutionकिसी समांतर चतुर्भुज ABCD में, `/_ D = 105^(@)` तो `/_ A ` तथा `/_ B` का माप बताएँ
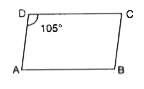
View Solutionयदि समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है तो सिद्ध करें कि वह दूसरे कोण को भी समद्विभाजित करेगा।
View Solutionएक समान्तर चतुर्भुज में, दर्शाइए कि दो आसन्न कोणों के कोण समद्विभाजक समकोण पर प्रतिच्छेद करते हैं।
View SolutionABCD एक समान्तर चतुर्भुज है, जिसकी भुजाएँ AB तथा DC पर क्रमशः L तथा M बिंदु हैं तथा AL = CM. सिद्ध करें कि LM तथा BD परस्पर समद्विभाजक हैं।
View Solutionयदि चतुर्भुज ABCD में `AB||CD` और `AD=BC` है तो सिद्ध कीजिए कि `/_A=/_B`
View SolutionABCD एक समान्तर चतुभुर्ज है। `AB` को E तक इस प्रकार बढ़ाया गया है की `BE=AB` सिद्ध कीजिए की `ED,BC` को समद्विभाजति करती है।
View SolutionPQRS एक समांतर चतुर्भुज है। RS को इस प्रकार बढ़ाया जाता है कि PX तथा QY क्रमशः P तथा Q से RS पर लंब है। सिद्ध कीजिए कि PX = QY
View Solutionदिए हुए `Delta ABC` में, A,B तथा C में तीन रेखाएँ इस प्रकार खींची जाती हैं, जो क्रमशः भुजाएँ BC,CA तथा AB के समान्तर हैं और `Delta PQR` बनाते हैं, तो सिद्ध कीजिए कि ` BC = ( 1)/( 2) QR`
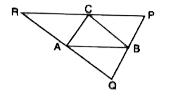
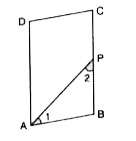
View Solutionआकृति में ABCD एक समान्तर चतुर्भुज हैं, जिसमें `/_ DAB = 60^(@)` , यदि `/_ A ` तथा `/_ B` के समद्विभाजक क्रमशः AP तथा BP भुजा CD के बिंदु P पर मिलते हैं, तो सिद्ध कीजिए कि बिंदु P भुजा CD का मध्य-बिंदु है।
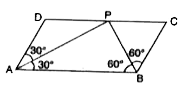
View Solutionएक समांतर चतुर्भुज ABCD में `/_ A` के समद्विभाजक भुजा BC को बिंदु P पर समद्विभाजित करता है। सिद्ध कीजिए कि `AD = 2AB`
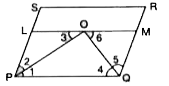
View Solutionआकृति में, PQRS एक समांतर चतुर्भुज हैं। PO तथा QO क्रमशः `/_ P` तथा `/_ Q` के समद्विभाजक हैं । PQ के समांतर रेखा lom खींची गई, तो सिद्ध कीजिए कि (i) PL = QM (ii) LO = OM
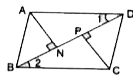
View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है और विकर्ण BD पर A तथा C से डालें गए लंब क्रमशः AN तथा CP हैं। सिद्ध कीजिए कि
(i) `Delta ADN ~= Delta CBP` (ii) AN = CP
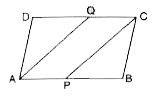
View Solutionआकृति में ABCD एक समान्तर चतुर्भुज है और P तथा Q क्रमशः सम्मुख भुजाओं AB और CD के मध्य-बिंदु है । सिद्ध कीजिए कि `square APCQ` एक समान्तर चतुर्भुज है।
View SolutionABCD एक समान्तर चतुर्भुज है। भुजा AD पर बिंदु P इस प्रकार है कि `AP = ( 1)/( 3) AD` तथा BC भुजा पर बिंदु Q इस प्रकार है कि `CQ = ( 1)/( 3) BC`. सिद्ध कीजिए कि `AQCP` एक समान्तर चतुर्भुज है।
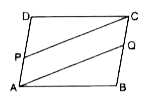
View Solution`square ABCD` एक समान्तर चतुर्भुज है तथा रेखाखण्ड AX तथा CY क्रमशः `/_ A` तथा `/_ C` के समद्विभाजक है। सिद्ध कीजिए कि `AX || CY`.
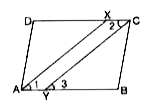
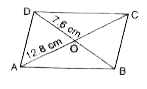
View Solutionकिसी समान्तर चतुर्भुज के विकर्ण AC तथा BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं और AC = 12.8 सेमी तथा BD = 7.6 सेमी है, तो OC तथा OD का मान निकालें।
View Solutionयदि दो रेखाखण्ड `AC` तथा `BD` परस्पर `O` पर समद्विभाजन करते है, तो सिद्ध कीजिए की `ABCD` एक समान्तर चतुभुर्ज है।
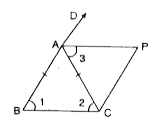
View Solutionआकृति में ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC. CP `||` AB तथा AP. `Delta ABC` के बहिष्कोण `/_ CAD` के समद्विभाजक है। सिद्ध कीजिए कि `/_ PAC = /_ BCA` तथा ABCP एक समान्तर चतुर्भुज है
View Solutionएक समांतर चतुर्भुज ABCD की भुजा AB का मध्य बिंदु `P` है। बिंदु B से होकर PD के समांतर रेखा DC को `Q` पर तथा बढ़ाई गई रेखा AD को `R` पर काटती है। सिद्ध कीजिए कि-
(i) `AR=2BC` (ii) `BR=2BQ`
View Solutionआकृति में, किसी समांतर ABCD चतुर्भुज के सम्मुख भुजाएँ AB तथा DC के मध्य - बिंदु क्रमशः R तथा S हैं। AS तथा DR को मिलाने से बिंदु P पर और CR तथा BS को मिलाने से बिंदु Q पर प्रतिच्छेदित होती है। सिद्ध कीजिए कि `square ABCD` एक समांतर चतुर्भुज है।
View Solution`Delta ABC` तथा `Delta DEF` दो त्रिभुज इस प्रकार हैं कि AB,DE के बराबर तथा समांतर हैं और BC, EF के बराबर तथा समांतर है। सिद्ध कीजिए कि AC,DF के बराबर तथा समांतर है।
View Solutionआकृति में समान्तर चतुर्भुज ABCD के `/_ A, /_ B ,/_C` तथा `/_ D` के मान निकालें।
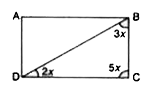
View SolutionAB और CD दो समान्तर रेखाएँ हैं। एक तिर्यक रेखा l,AB को R पर तथा CD को S पर प्रतिच्छेद करती है। सिद्ध कीजिए कि अन्तःकोणों के कोण समद्विभाजक एक आयत बनाते हैं।
View Solutionकिसी `Delta ABC` में माध्यिका AD को P तक इस प्रकार बढ़ाया जाता है कि`AD = DP` । सिद्ध कीजिए कि ABPC एक समांतर चतुर्भुज है।
View Solutionएक समान्तर चतुर्भुज के विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। O से होकर जाने वाली एक रेखा भुजा AB को X पर तथा भुजा DC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए OX = OY
View Solutionआयत के प्रत्येक कोण समकोण होते हैं।
View SolutionABCD एक आयत है, जिसमें `/_ BAC = 32^(@)`, तो `/_ DBC` का मान ज्ञात कीजिए।
View SolutionABCD आयत के विकर्ण का प्रतिच्छेद बिंदु O है। यदि `/_ BOC = 44^(@)` तो `/_ OAD` का मान ज्ञात करें।
View Solutionसाबित करें कि समांतर चतुर्भुज के कोणों के समद्विभाजक एक आयत बनाते हैं।
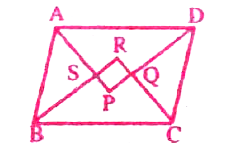
View Solutionसमचतुर्भुज एक समान्तर होता है, जिसके आसन्न भुजाएँ बराबर होते हैं , तो सिद्ध करें कि समचतुर्भुज की प्रत्येक भुजा समान लम्बाई की होती है।
View Solutionएक समचतुर्भुज है, जिसमें परिकलित करें।
View SolutionPQRS एक वर्ग है। PR और SQ,O पर प्रतिच्छेदित होते हैं। `/_ POQ` का माप ज्ञात करें।
View SolutionPQRS एक वर्ग है। `/_ SRP` परिकलित करें
View Solutionसिद्ध कीजिए कि एक वर्ग की भुजाओं के मध्य बिंदुओं को मिलाकर बनाया गया चतुर्भुज एक वर्ग ही है।
View Solutionआकृति में, ABCD एक चतुर्भुज है, जिसमें AB = BC और AD =CD. (इस पतंगाकार आकृति में ) सिद्ध करें कि
`Delta ABD ~= Delta CBD` और इसलिए DB, `/_ ADC` का समद्विभाजक है और BD, `/_ ABC` का समद्विभाजक है।
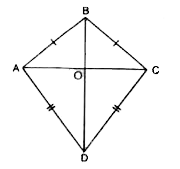
View Solutionआकृति में, ABCD एक चतुर्भुज है, जिसमें AB = BC और AD =CD. (इस पतंगाकार आकृति में ) सिद्ध करें कि
`Delta AOD ~= Delta COD ` इस प्रकार `/_ AOD = /_ COD=1` समकोण
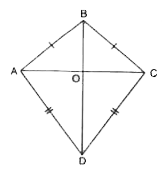
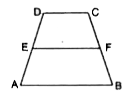
View Solutionआकृति में, E समलम्ब ABCD के भुजा AD का मध्य-बिंदु है, जिसमें AB `||` DC. AB के समान्तर E से होकर जाती हुई एक रेखा BC से F पर मिलती है। सिद्ध कीजिए कि F,BC का मध्य-बिंदु है।
View SolutionE व F क्रमशः समतल चतुर्भुज `ABCD` की असमान्तर भुजाओं के मध्य बिन्दु है। सिद्ध कीजिए की
(i) `EF||AB `
(ii)` EF=(1)/(2)(AB+CD)`
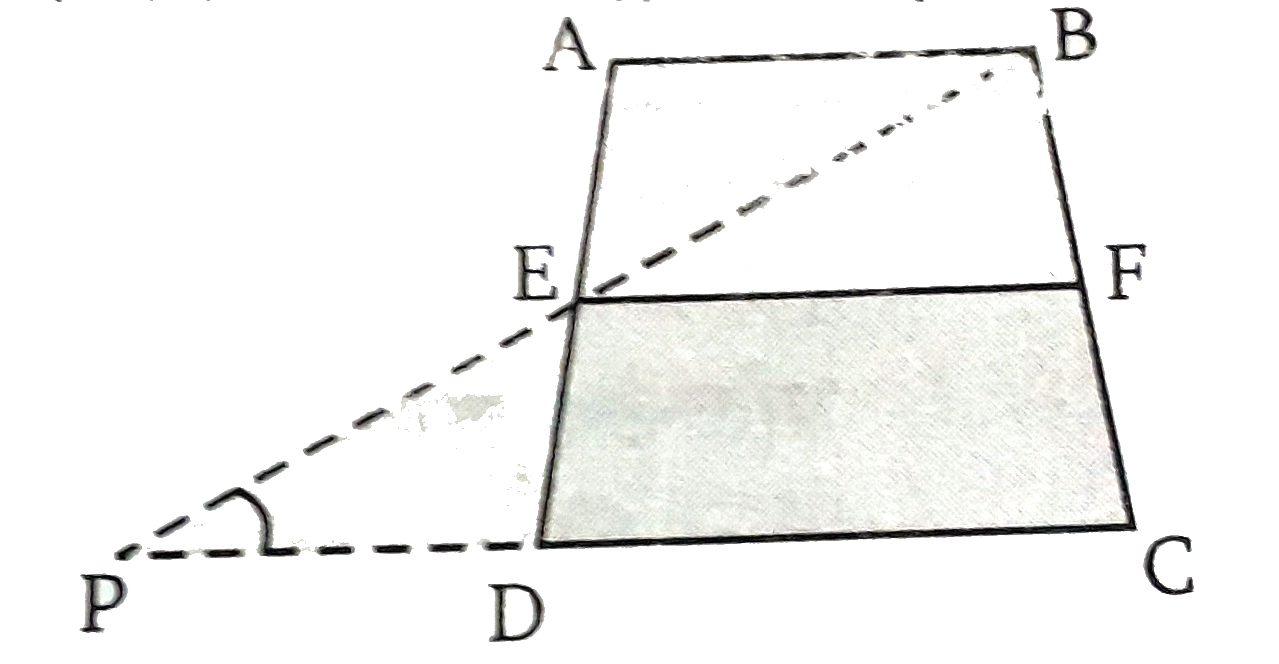
View Solutionसमलम्ब के दो असमान्तर भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखाखण्ड समांतर भुजाओं के समांतर होती है।
View Solution`DeltaABC` की भुजा AB को बिंदु `M` और `N` समत्रिभाजित करते हैं । दो रेखाखण्ड `MP` और `NQ,BC` के समांतर है जो `AC` से `P` और `Q` बिंदुओं पर मिलते हैं। सिद्ध कीजिए कि `P` और `Q` भुजा AC के समत्रिभाग करते हैं।
View Solutionसंलग्न चित्र में दो बिंदु A और B रेखा `l` के एक ही और स्थित है। AB का मध्य बिंदु C है। यदि `AD_|_l` तथा `BE_|_l` तो सिद्ध कीजिए कि `CD=CE`

View Solutionसिद्ध करें कि एक त्रिभुज के शीर्ष से उसके आधार पर खींची गई कोई सरल रेखा उस सरल रेखा द्वारा समद्विभाजित होती है, जो त्रिभुज के अन्य भुजाओं के मध्य-बिंदुओं को मिलाता है।
View Solution
साधित उदाहरण questions and complete solutions for chapter समान्तर चतुर्भुज of S CHAND of Class 9