Complete Solutions to साथित उदाहरण of chapter क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | क्षेत्रफल |
| S CHAND | साथित उदाहरण |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
एक समांतर चतुर्भुज ABCD में `AB=8` सेमी है। भुजाएं AB व AD के संगत शीर्षलम्ब क्रमशः 4 व 5 सेमी हैं। AD का मान ज्ञात कीजिए।
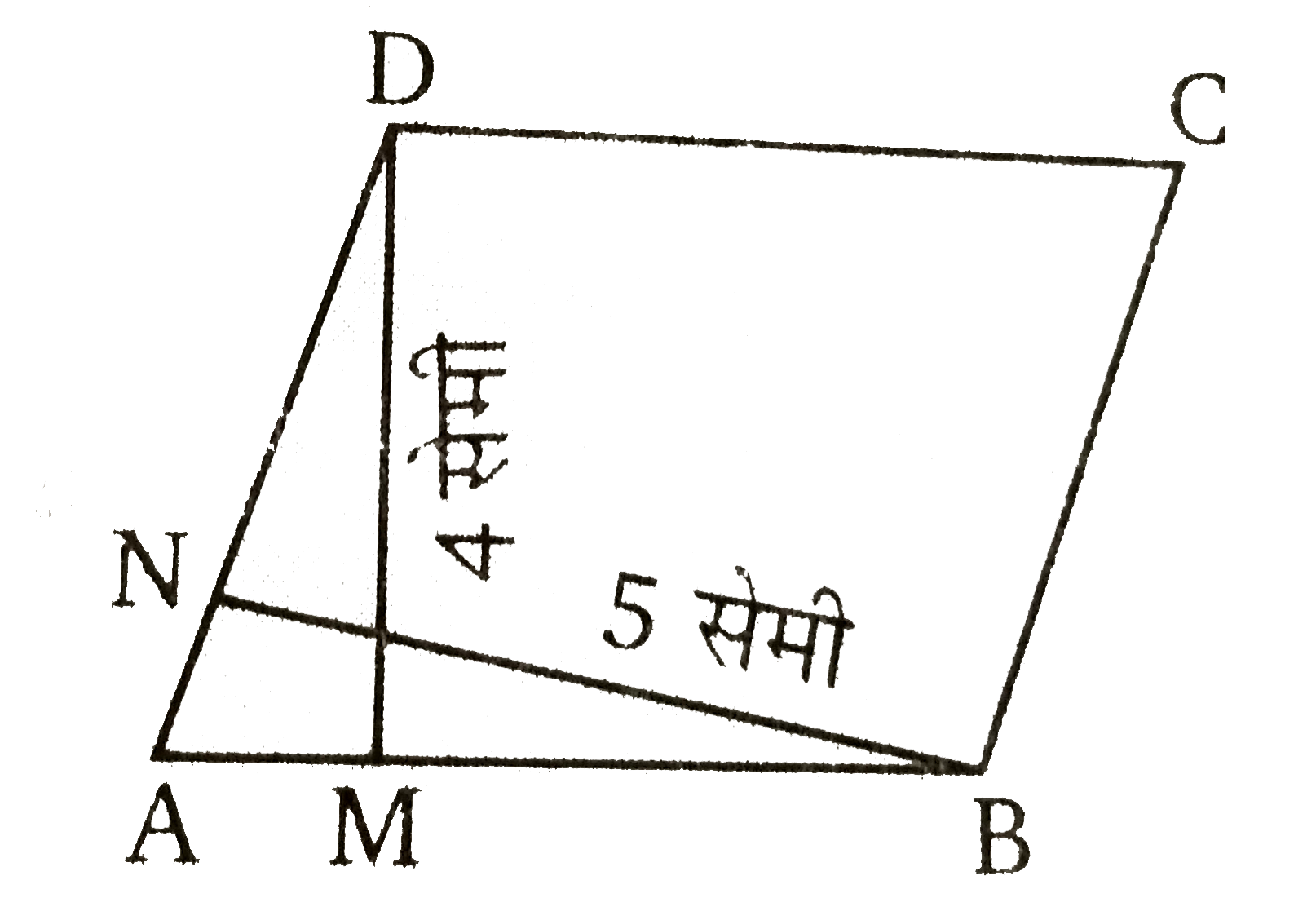
View Solutionसिद्ध करें कि एक समान्तर चतुर्भुज के सम्मुख के मध्य-बिंदुओं को मिलाने वाली रेखाखण्ड इसे दो बराबर समान्तर चतुर्भुज में विभाजित करता है।
View Solutionसमान्तर चतुर्भुज ABCD के विकर्ण, बिंदु O पर प्रतिच्छेद करते हैं। O से, एक रेखा खींची गई है जो AB को X पर तथा CD को Y पर प्रतिच्छेद करती है। दर्शाइए कि XY समान्तर चतुर्भुज को दो भागों में विभाजित करती है , जिनके क्षेत्रफल बराबर है।
View Solutionसिद्ध करें कि दी हुई भुजाओं वाले सभी समान्तर चतुर्भुज में सबसे अधिक क्षेत्रफल वाला समान्तर चतुर्भुज एक आयत होता है।
View Solutionएक समान्तर चतुर्भुज और एक आयत का आधार उभयनिष्ठ है और क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाण से बड़ा है।
View SolutionABC एक त्रिभुज है और AD इसकी एक माध्यिका है। AD पर कोई एक बिंदु X हैं। दर्शाइए कि क्षेत्रफल `Delta ABX` = क्षेत्रफल `Delta ACX`
View Solutionदो त्रिभुज ABC और DBC एक ही आधार BC पर हैं और उनके शीर्ष A और D रेखा BC, के विपरीत ओर स्थित हैं, जिससे कि क्षेत्रफल `Delta ABC =` क्षेत्रफल `Delta DBC` । दर्शाइए कि BC रेखाखण्ड AD को समद्विभाजित करता है।
View SolutionABC के त्रिभुज है जिसमें D,BC का मध्य-बिंदु है तथा E,AD का मध्य-बिंदु है। दर्शाइए कि क्षेत्रफल `Delta BED = ( 1)/( 4)` क्षेत्रफल `Delta ABC`
View Solution`Delta ABC` की माध्यिकाएँ AD,BE और CF,G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि क्षेत्रफल `Delta AGB =` क्षेत्रफल` Delta AGC=` क्षेत्रफल `Delta BGC = ( 1)/( 3)` क्षेत्रफल `Delta ABC`
View Solutionयदि D,E तथा F क्रमशः `Delta ABC` की भुजाओं BC,CA तथा AB के मध्य-बिंदु हैं, तो सिद्ध करें कि BDEF एक समान्तर चतुर्भुज हैं, जिसका क्षेत्रफल `Delta ABC` के क्षेत्रफल का आधा है। यदि भी सिद्ध करें कि क्षेत्रफल `Delta DEF = ( 1)/( 4) ` क्षेत्रफल `Delta ABC`
View Solutionसिद्ध करें कि त्रिभुज कि माध्यिका इसे बराबर क्षेत्रफल वाले दो त्रिभुओं में विभाजित करती है।
View Solutionएक समबाहु त्रिभुज में O त्रिभुज के अभ्यन्तर में स्थित कोई बिंदु है । O से त्रिभुज की भुजाओं पर लंब डाले गए हैं। सिद्ध करें कि इन लंब रेखाख़ण्डों का योगफल एक अचर है।
View Solutionसिद्ध करें कि एक समबाहु त्रिभुज का क्षेत्रफल `( sqrt( 3))/( 4) a^(2)` होता है, जहाँ त्रिभुज की भुजा है ।
View Solutionसंलग्न आकृति में, `Delta ABC` की भुजा AB का मध्य बिंदु D है तथा P भुजा BC पर कोई बिंदु है। CQ `||` PD, AB को Q पर प्रतिच्छेद करती है। सिद्ध करें क्षेत्रफल `Delta BPQ = (1)/(2)` क्षेत्रफल `Delta ABC`
View SolutionABCD एक चतुर्भुज है तथा इसके विकर्ण AC और BD,O पर प्रतिच्छेद करते हैं। सिद्ध करें कि यदि BO=OD तो त्रिभुज ABC और ADC के क्षेत्रफल बराबर है।
View Solutionयदि एक चतुर्भुज का प्रत्येक विकर्ण इसे बराबर वाले दो त्रिभुजों में विभाजित करता है, तो सिद्ध करें कि यह चतुर्भुज एक समान्तर चतुर्भुज है।
View Solutionसमान्तर चतुर्भुज ABCD में E तथा क्रमशः भुजाओं AB तथा BC पर स्थित दो बिंदु हैं। सिद्ध करें कि क्षेत्रफल `Delta ADF =` क्षेत्रफल `Delta DCE`
View Solutionसिद्ध करें कि समांतर चतुर्भुज के विकर्ण इसे बराबर क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं।
View Solutionयदि चतुर्भुज ABCD के विकर्ण AC तथा BD,O पर प्रतिच्छेद करते हैं तथा चतुर्भुज ABCD को बराबर क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं, तो सिद्ध कीजिए कि चतुर्भुज ABCD एक समान्तर चतुर्भुज हैं।
View SolutionABCD एक समान्तर चतुर्भुज है तथा P इसके बीच अभ्यन्तर में कोई एक बिंदु है। सिद्ध करें कि क्षेत्रफल `Delta APB ` क्षेत्रफल `Delta CPD` = क्षेत्रफल`Delta BPC+` क्षेत्रफल `Delta APD`
View Solutionएक आयत ABCD के अंतर स्थित एक बिंदु O को इसके शीर्षों से मिलाया गया है। सिद्ध करें कि इस तरह से बने दो सम्मुख त्रिभुजों का योग शेष दो त्रिभुजों के क्षेत्रफल के योग के बराबर है।
View SolutionE,F,G,H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं AB,BC,CD तथा DA के मध्य-बिंदु हैं। सिद्ध करें कि चतुर्भुज एक समान्तर चतुर्भुज हैं और इसका क्षेत्रफल समान्तर चतुर्भुज ABCD के क्षेत्रफल का आधा है।
View Solutionदो बिंदु A और B एक धनात्मक वास्तविक संख्या x दिए हुए हैं। ऐसे बिंदु P का बिन्दुपथ ज्ञात करें कि क्षेत्रफल `Delta PAB =x ` हो।
View Solutionसिद्ध करें कि समचतुर्भुज का क्षेत्रफल `= ( 1)/( 2) xx ` विकर्णों का गुणनफल
View Solution
साथित उदाहरण questions and complete solutions for chapter क्षेत्रफल of S CHAND of Class 9