Complete Solutions to प्रश्नावली 27.1 of chapter त्रिकोणमितीय of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिकोणमितीय |
| S CHAND | प्रश्नावली 27.1 |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
आकृति से `sinA,cosA,tanA,cosecA,secA` तथा `cotA` के मान ज्ञात कीजिए।
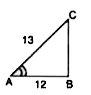 04:49View Solution
04:49View Solution`DeltaABC` में `angleB` समकोण है। भुजा `AB=4` सेमी तथा `BC=3` सेमी और `CA=5` सेमी हो, तो `sinA,tanA,cosC` तथा `cotC` के मान ज्ञात कीजिए।
02:28View Solutionयदि `sintheta=(sqrt3)/(2)` हो, तो शेष त्रिकोणमितीय अनुपातों के मान ज्ञात कीजिए।
03:25View Solutionयदि `cosecA=(7)/(4)` हो, तो सिद्ध कीजिए कि `1+tan^(2)A=sec^(2)A`.
04:11View Solutionयदि `sectheta=(5)/(4)` हो, तो सिद्ध कीजिए कि `cos^(2)A=1-sin^(2)A`.
03:39View Solutionयदि `tanA=(2)/(3)` हो, तो सिद्ध कीजिए कि `sin^(2)A+cos^(2)A=1`.
03:02View Solutionयदि `tanA=(1)/(3)` हो तो सिद्ध कीजिए कि `cosec^(2)A=1+cot^(2)A`
02:42View Solutionयदि `cos theta =1/2 ` हो, तो `(2 sec theta)/(1+tan ^(2)theta )` का मान ज्ञात करो।
01:43View Solutionयदि `sinA=(4)/(5)` हो, तो `(sinA-cotA)/(2tanA)` का मान ज्ञात कीजिए।
03:28View Solutionयदि `4tanA=3`, तो `((4sinA-cosA)/(4sinA+cosA))` का मान है :
04:02View Solutionयदि `cotA=2` हो तो `(4cosA+2sinA)/(5cosA-2sinA)` का मान ज्ञात कीजिए।
02:03View Solutionयदि `sinA=(12)/(13)` हो, तो `(sin^(2)A-cos^(2)A)/(2sinAcosA)xx(1)/(tan^(2)A)` का मान ज्ञात कीजिए।
05:33View Solutionयदि `3cotA=2` हो, तो `(4sinA-3cosA)/(2sinA+6cosA)` का मान ज्ञात कीजिए।
02:51View Solutionयदि `sec A =(5)/(4)` , तो प्रदर्शित कीजिए कि `(3 sin A -4 sin^(3)A)/(4 cos^(3)a -3 cos A )=(3 tan A -tan^(3) A )/( 1-3 tan^(2)A)`
06:40View Solutionयदि `sinA=(1)/(3)` हो, तो सिद्ध कीजिए कि `cosAcosecA+tanAsecA=(16sqrt2+3)/(8)`
04:06View Solutionयदि `tan theta=sqrt2-1,` तो सिद्ध कीजिए कि `sin theta cos theta = (sqrt2)/(4)`
08:51View Solutionयदि `tanA=1`और `tanB=sqrt3,` तो निम्नलिखित का मान ज्ञात कीजिए: `cosAcosB-sinA sinB.`
02:18View Solutionयदि `DeltaABC` में, `/_C=90^(@)` एवं `tanA=(1)/(sqrt(3))` हो तो सिद्ध करे कि
`sinA*cosB+cosA*sinB=1`03:07View Solutionयदि `tantheta=(2mn)/((m^(2)-n^(2)))` हो, तो शेष त्रिकोणमितीय अनुपातों का मान ज्ञात कीजिए।
03:20View Solutionयदि `tantheta=(p)/(q)` तो दिखाइए कि `(p sintheta-qcostheta)/(p sintheta+qcostheta)=(p^(2)-q^(2))/(p^(2)+q^(2))`
04:06View Solutionयदि `sin theta =(a^2-b^(2))/(a^(2)+b^(2))` हो , तो कोण ` theta ` के अन्य त्रिकोणमितीय अनुपात ज्ञात करो ।
06:16View Solutionयदि `tan theta=(20)/(21)` हो, तो सिद्ध कीजिए कि `(1-sintheta+costheta)/(1+sintheta+costheta)=(3)/(7)`
04:40View Solutionयदि `tantheta=(m)/(n)` हो, तो सिद्ध कीजिए कि `(msintheta-ncostheta)/(msintheta+ncostheta)=(m^(2)-n^(2))/(m^(2)+n^(2))`
03:27View Solutionयदि `costheta=(2t)/(1+t^(2))` हो, तो `cosectheta` तथा `cot theta` के मान ज्ञात कीजिए।
03:29View Solutionयदि `tantheta+sectheta=4` हो, तो `sintheta` तथा `costheta` के मान ज्ञात कीजिए।
03:10View Solutionयदि `tanA=2` हो, तो सिद्ध करे कि
`sinA.secA+tanA-cosecA=(8-sqrt(5))/(2)`03:20View Solutionयदि `7sinA=24cosA` हो, तो सिद्ध कीजिए कि `14tanA+25cosA-7secA=30`.
02:34View Solutionयदि `sec A =(5)/(4)` , तो प्रदर्शित कीजिए कि `(3 sin A -4 sin^(3)A)/(4 cos^(3)a -3 cos A )=(3 tan A -tan^(3) A )/( 1-3 tan^(2)A)`
06:40View Solutionयदि हुआ है `cotA=(4)/(3)`, तो सिद्ध कीजिए कि `(cos^(2)A-sin^(2)A)/(cosA)=(1-tan^(2)A)/(secA)`
03:51View Solutionआकृति से, `3sintheta-4sin^(3)theta` का मान ज्ञात कीजिए।
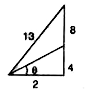 05:38View Solution
05:38View Solution
प्रश्नावली 27.1 questions and complete solutions for chapter त्रिकोणमितीय of S CHAND of Class 9
