Complete Solutions to EXERCISE 11.3 of chapter AREA OF PARALLELOGRAMS AND TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | AREA OF PARALLELOGRAMS AND TRIANGLES |
| SUBHASH PUBLICATION | EXERCISE 11.3 |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
In the figure 11.23, E is any point on median AD of a `Delta`ABC. Show that ar (ABE) = ar (ACE).
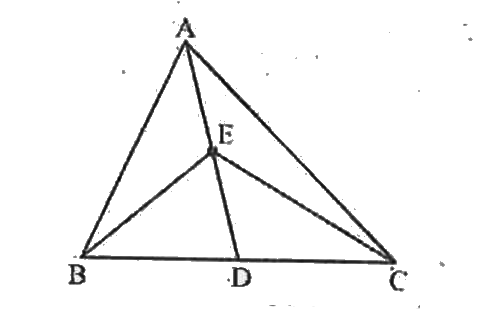
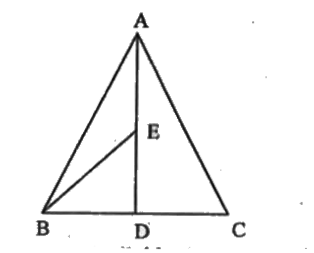
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = `(1)/(4)` ar (ABC).
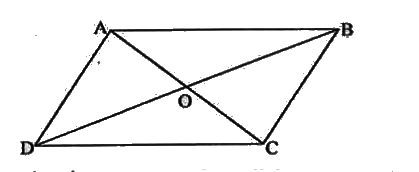
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
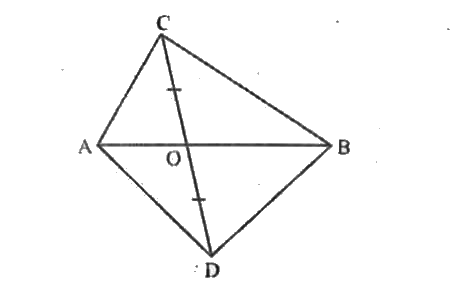
View SolutionIn, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
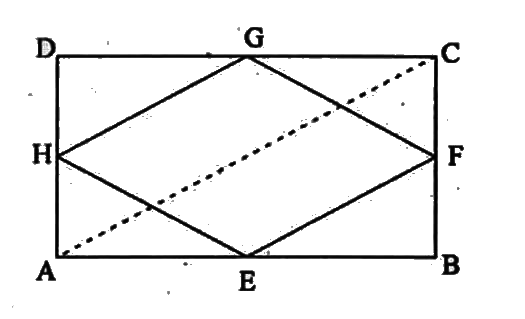
View SolutionIf E,F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = `(1)/(2)` ar (ABCD)
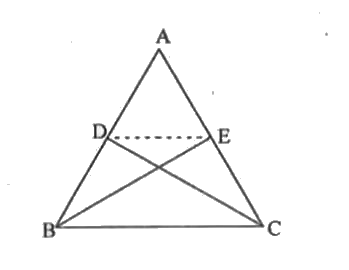
View SolutionD and E are points on sides AB and AC respectively of `Delta` ABC such that ar (DBC) = ar EBC). Prove that DE`|\|`BC.
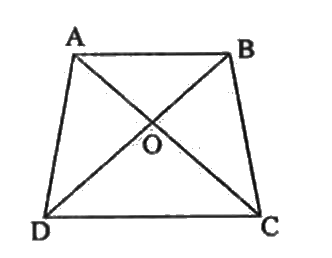
View SolutionDiagonals AC and BD of a trapezium ABCD with AB`|\|`DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
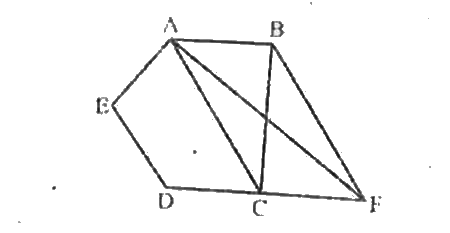
View SolutionIn, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i)ar (ACB) = ar (ACF)
(ii)ar (AEDF) = ar(ABCDE)
View Solution
EXERCISE 11.3 questions and complete solutions for chapter AREA OF PARALLELOGRAMS AND TRIANGLES of VIDHYASANGAM - RAO'S ACADEMY MATHS (KANNADA ENGLISH) of Class 9