Complete Solutions to Example of chapter చతుర్భుజాలు of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | చతుర్భుజాలు |
| VGS PUBLICATION-BRILLIANT(TELUGU) | Example |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
ABCD సమాంతర చతుర్భుజం మరియు `/_A=60^@` మిగిలిన కోణాల కొలతలు కనుగొనండి.
View SolutionABCD సమాంతర చతుర్భుజం మరియు `/_DAB=40^@` అయిన మిగిలిన కోణాల కొలతలు కనుగొనండి.
View Solutionసమాంతర చతుర్భుజములో రెండు అసన్నభుజాలు వరుసగా 4.5 సెంమీ. మరియు 3 సెమీ దాని చుట్టుకొలత కనుగొనుము.
View SolutionABCD సమాంతర చతుర్భుజములో పక్కకవనాలు `/_A` మరియు `/_B` యొక్క సమద్విఖండన P వద్ద ఖండించుకున్నాయి. అయిన `/_APB = 90^@` అని చూపండి.
View Solutionఒక సమాంతర చతుర్భుజకరంలో కాగితాన్ని కత్తిరించండి. దాని కర్ణం వెంబడి మరలా కత్తిరించండి. ఎటువంటి ఆకారాలు ఏర్పడ్డాయి? ఈ రెండు త్రిభుజాలను గూర్చి మీరు ఏమి చెబుతారు?
View Solutionసమాంతర చయతృభూజమును కర్ణం రెండు సర్వసమాన త్రిభుజాలుగా విభజయిస్తుంది.
View Solutionసమాంతర చతుర్భుజము ఎదుటి భుజాలు సమానము.
View Solutionఒక చతుర్భుజములో ప్రతి జత ఎదుటి కోణాలు సమానము అయితే, అది సమాంతర చతుర్భుజమగును.
View Solutionఒక చతుర్భుజములో ప్రతి జత ఎదుటి కోణాలు సమానము అయితే, అది సమాంతర చతుర్భుజమగును.
View Solutionఒక చతుర్భుజంలో కర్ణములు పరస్పరం సమద్విఖండన చేసుకుంటే అది సమాంతర చతుర్భుజము అగును.
View Solutionఒక చతుర్భుజంలో కర్ణములు పరస్పరం సమద్విఖండన చేసుకుంటే అది సమాంతర చతుర్భుజము అగును.
View Solutionదీర్ఘచతురస్రం లో ప్రతికోణము లంబకోణము అని నిరూపించండి.
View Solutionరాంబస్ లో కర్ణాలు పరస్పరం లంబలుగా ఉంటాయని చూపండి.
View SolutionABCD సమాంతర చతురభజములో AC కర్ణం `/_A` ను సమద్వి ఖండన చేస్తే ABCD ఒక రాంబస్ అవుతుందని నిరూపించండి.
View Solutionధీర్ఘచతురస్రం లో కర్ణాలు సమానమని నిరూపించండి.
View Solutionసమాంతర చతుర్భుజములో కోణ సమద్విఖండన రేఖలు ధీర్ఘచతురస్రన్ని ఏర్పరుస్తాయని చూపండి.
View Solutionచతురస్రంలో కర్ణాలు సమానమని , అవి పరస్పరం లంబ సమద్విఖండన చేసుకుంటాయని చూపండి.
View Solutionరాంబస్ లో కర్ణాలు దానిని 4 సర్వసమాన త్రిభుజాలుగా విభజిస్తాయని నిరూపించండి.
View Solution`bar AB` మరియు `bar DC` రెండు సమాంతర రేఖలు. తిర్యగ్రేఖ l, `bar AB` ని P వద్ద `bar DC` ని R వద్ద ఖండించింది. అయిన అంతర కోణాలు సమద్విఖండన రేఖలు ధీర్ఘచతురసరాన్ని ఏర్పరుస్తాయని చూపండి.

View Solution`Delta ABC` లో BC భుజం మీదకు మధ్యగతం AD గీయబడినది. AD = ED అగునట్లు E వరకు పొడిగించబడినది. అయిన ABEC ఒక సమాంతర చతుర్భుజన్ని నిరూపించండి.
View Solutionక్రింది పటంలో D, E లు AB మరియు AC ల మధ్య బిందువులు DE=4 సెంమీ, అయిన BC=
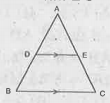
View Solutionఒక త్రిభుజములో రెండు భుజాల మధ్య బిందువులను కలుపుతూ గీయబడిన రేఖ, మూడవ భుజానికి సమంతరముగాను, మరియు దానిలో సగము ఉంటుంది.
View Solutionఒక త్రిభుజాములో ఒక భుజము మధ్య బిందువు గుండా పోయేరేఖ, రెండవ భుజానికి సమాంతరంగా ఉంటే అది మూడవ భుజాన్ని సమద్విఖండన చేస్తుందని చూపండి. (ప్రాథమిక అనుపాత సిద్దాంతమునుపయోగించి).
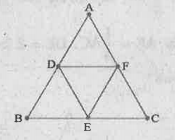
View Solution`Delta ABC ` లో D,E మరియు F లు వరుసగా AB,BC మరియు CA భుజాల మధ్యబిందువులు. వీటిని ఒకదానితో మరొకటి కలుపగ ఏర్పడిన నాలుగు త్రిభుజాలు సర్వసమనలని చూపండి.
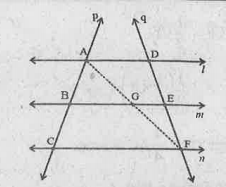
View Solutionl,m మరియు n అనే 3 సమాంతర రేఖలను p మరియు q అనే రెండు తిర్యగ్రేఖలు A,B,C మరియు D,E,F ల వద్ద ఖండించాయి. తిర్యగ్రేఖ p, ఈ సమాంతర రేఖలను రెండు సమాన అంతరఖండలు AB,BC లుగా విభజిస్తే q తిర్యగ్రేఖ కూడా సమాన అంతరఖండలు DE మరియు EF లుగా విభజయిస్తుందని చూపండి .
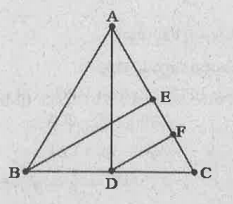
View Solution`Delta ABC` లో AD మరియు BE లు రెండు మధ్యగత రేఖలు మరియు `BE |\| DF` అయిన `CF = 1/4 AC` అని చూపండి.
View SolutionABC త్రిభుజంలో BC,CA మరియు AB భుజాలకు సమాంతరంగా A,B మరియు C ల గుండా సమాంతర రేఖలు గిస్తే అవి P,Q మరియు R ల వద్ద ఖండించుకున్నాయి. `Delta PQR` త్రిభుజము చుట్టుకొలత `Delta ABC` త్రిభుజము చుట్టుకోలాటకు రెట్టింపు ఉంటుందని చూపండి.
View Solution
Example questions and complete solutions for chapter చతుర్భుజాలు of VGS MATHS (TELUGU) of Class 9