Complete Solutions to Exercise of chapter చతుర్భుజాలు of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | చతుర్భుజాలు |
| VGS PUBLICATION-BRILLIANT(TELUGU) | Exercise |
| Number Of Questions | 88 |
| Academic Year | 2023-24 |
కింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. ప్రతి సమాంతర చతుర్భుజము ఒక ట్రెపీజియం అగును.
View Solutionకింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. అన్నీ సమాంతర చతుర్భుజలు, చతుర్భుజలే.
View Solutionకింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. అన్నీ ట్రెపీజియం లు , సమాంతర చతుర్భుజలే.
View Solutionకింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. చతురస్రము అనేది రాంబస్ అవుతుంది.
View Solutionకింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. ప్రతి రాంబస్ కూడా ఒక చతురస్రము.
View Solutionకింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. అన్నీ సమాంతర చతుర్భుజలు, ధీర్ఘచతురసరలే.
View Solutionకింది పట్టికలో చతుర్భుజ ధర్మాలు ఆయా పటాలకు వర్తిస్తే "అవును" అని , వర్తించకపోతే "కాదు" అని రాయండి.
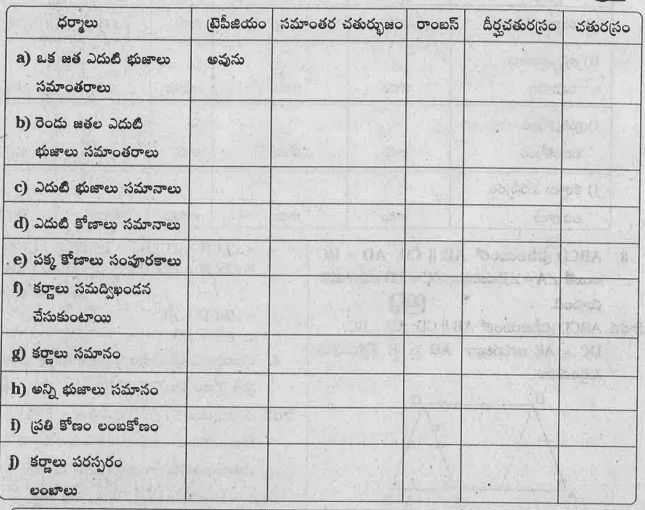
View SolutionABCD ట్రెపీజియంలో `AB |\| CD` . AD=BC అయితే `/_A = /_ B` మరియు `/_C=/_D` అవుతాయాని చూపండి.
View Solutionచతుర్భుజంలో కోణాల నిష్పత్తి `1 :2 :3 : 4` అయిన ప్రతి కోణం కొలతను కనుగొనండి.
View SolutionABCD ఒక ధీర్ఘచతురస్రము AC కర్ణం అయిన ` Delta ACD` లో కోణాలను కనుగొనండి. కారణాలు తెలపండి.
View SolutionABCD ఒక సమాంతర చతుర్భుజము మరియు ABEF ఒక ధీర్ఘచతురస్రము అయిన `Delta AFD ~= Delta BEC` అని చూపండి.
View Solutionరాంబస్ లో కర్ణాలు దానిని 4 సర్వసమాన త్రిభుజాలుగా విభజిస్తాయని నిరూపించండి.
View SolutionABCD చతుర్భుజములో `/_C` మరియు` /_D` ల యొక్క సమద్వి ఖండన రేఖలు O వద్ద ఖండించుకుంటే `/_COD = 1/2 (/_A + /_B)` అని చూపండి.
View Solutionసమాంతర చతుర్భుజము ఎదుటి కోణాలు `(3x-2)^@` మరియు `(x+48)^@` అయిన సమాంతర చతుర్భుజములో ప్రతి కోణాన్ని కనుగొనండి.
View Solutionసమాంతర చతుర్భుజములో ఒక కోణం , అతి చిన్న కోణమునకు రెట్టింపు కన్నా `24^@` తక్కువ అయిన సమాంతర చతుర్భుజంలో అన్నీ కోణాలను కనుగొనుము.
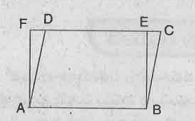
View Solutionకింది పటంలో ABCD ఒక సమంతార చతుర్భుజము. BC యొక్క మధ్య బిందువు E . AB మరియు DE లను F వరకు పొడిగించిన,AF = 2AB అని నిరూపించండి.
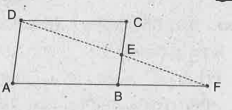
View Solutionకింది పటంలో ABCD ఒక సమంతార చతుర్భుజము. AB,DC ల యొక్క మధ్య బిందువు P మరియు Q లు అయిన PBCQ ఒక సమాంతర చతుర్భుజమని చూపండి.
View SolutionABC ఒక సమద్విబహు త్రిభుజము మరియు AB=AC . బాహ్యకోణం QAC నకు AD సమద్విఖండన రేఖ అయితే `/_DAC = /_BCA`
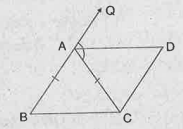
View SolutionABC ఒక సమద్విబహు త్రిభుజము మరియు AB=AC . బాహ్యకోణం QAC నకు AD సమద్విఖండన రేఖ అయితే ABCD ఒక సమాంతర చతుర్భుజమని చూపండి.
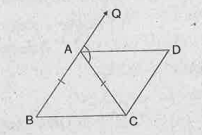
View SolutionABCD is a parallelogram AP and CQ are perpendiculars drawn from vertices A and C on diagonal BD (see figure) show that
(i) `DeltaAPB ~= DeltaCQD`
(ii) `AP = CQ`
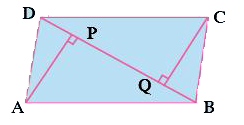
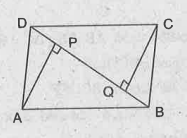
View SolutionABCD సమాంతర చతుర్భుజము AP మరియు CQ లు శీర్షాలు A మరియు C ల నుండి కర్ణం BD పైకి గీచిన లంబాలు అయిన AP = CQ అని చూపండి.
View Solution`Delta ABC` మరియు `Delta DEF` లలో `AB//DE,AB=DE, BC=EF` మరియు `BC //EF`. శీర్షాలు A,B మరియు C లు వరుసగా D,E మరియు F లకు కలుపబడినవి అయిన ABED ఒక సమాంతర చతుర్భుజము
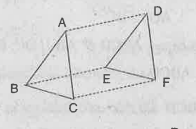
View Solution`Delta ABC` మరియు `Delta DEF` లలో AB // DE, BC=EF మరియు BC // EF. శీర్షాలు A,B మరియు C లు వరుసగా D,E మరియు F లకు కలుపబడినవి అయిన BCEF ఒక సమాంతర చతుర్భుజము
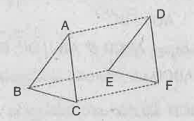
View SolutionΔABC మరియు ΔDEF లలోAB=DE, BC=EF మరియు BC//EF. శీర్షాలు A,B మరియు C లు వరుసగా D,E మరియు F లకు కలుపబడినవి అయిన AC=DF
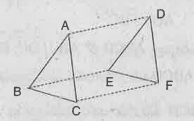
View SolutionΔABC మరియు ΔDEF లలోAB=DE,BC=EF మరియు BC//EF. శీర్షాలు A,B మరియు C లు వరుసగా D,E మరియు F లకు కలుపబడినవి అయిన ΔABC≅ΔDEF అని చూపండి.
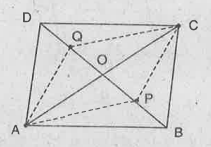
View SolutionABCD ఒక సమాంతర చతుర్భుజము. AC మరియు BD లు 'O' వద్ద ఖండించుకున్నాయి. P,Q లు BD కర్ణం పై త్రీథాకరించబడిన బిందువులైన CQ // AP మరియు AC కర్ణం, PQ ను సమద్విఖండన చేయునని చూపండి.
View SolutionABCD ఒక చతురస్రము. E,F,G మరియు H లు వరుసగా AB,BC,CD మరియు DA లపై గల బిందువులు AE=BF=CF=DH అయినచో EFGH ఒక చతురస్రమనీ చూపండి.
View SolutionABC త్రిబుజంలో AB పై D ఒక బిందువు మరియు `AD=1/4 AB` . ఇదే విధంగా AC పై బిందువు E మరియు `AE=1/4 AC`. DE = 2 సెమీ అయిన BC ఎంత?
View SolutionABCD చతుర్భుజములో AB,BC,CD మరియు DA ల మధ్య బిందువులు E,F,G మరియు H లు అయిన EFGH సమాంతర చతుర్భుజమని నిరూపించుము.
View Solutionదీని భుజల మధ్య బిందువులను కలుపుట ద్వారా రాంబస్ ఏర్పడును
View SolutionABCD సమాంతర చతుర్భుజములో AB,DC ల మధ్య బిందువలు వరుసగా E మరియు F అయిన AF మరియు EC రేఖకండాలు కర్ణము BD ని త్రిథాకరిస్తాయని చూపండి.
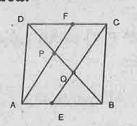
View Solutionచతుర్భుజంలో ఎదుటి భుజాల మధ్య బిందువులకు కలుపుతూ గీయబడియా రేఖఖండలు సమద్విఖండన చేసుకుంటాయని చూపండి.
View SolutionABC లంబకోణ త్రిభుజాములో C లంబకోణం. కర్ణం AB మధ్యబిందువు M గుండా BC కు సమంతరముగా గీచిన రేఖ AC ని D వద్ద ఖండిస్తే కింది వానిని నిరూపించండి AC మధ్య బిందువుD
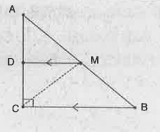
View SolutionABC లంబకోణ త్రిభుజాములో C లంబకోణం. కర్ణం AB మధ్యబిందువు M గుండా BC కు సమంతరముగా గీచిన రేఖ AC ని D వద్ద ఖండిస్తే కింది వానిని నిరూపించండి `MD _|_ AC`
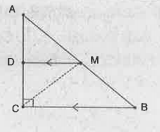
View SolutionABC లంబకోణ త్రిభుజాములో C లంబకోణం. కర్ణం AB మధ్యబిందువు M గుండా BC కు సమంతరముగా గీచిన రేఖ AC ని D వద్ద ఖండిస్తే కింది వానిని నిరూపించండి `CM=MA = 1/2 AB`
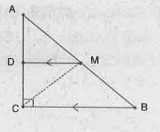
View Solutionచతుర్భుజం PQRS యొక్క ఎదుటి శీర్షాలు
View Solutionసమాంతర చతుర్భుజములోని ఆసన్న భుజాలు 4.7 సెంమీ మరియు 6.3 సెంమీ లయిన దాని చుట్టుకొలత
View Solutionసమాంతర చతుర్భుజములోని రెండు భుజాలు 8 సెంమీ మరియు 3 సెంమీ లయిన దాని చుట్టుకొలత
View SolutionPQRS సమాంతర చతుర్భుజంలో `/_P=40^@` అయిన `/_R`=
View SolutionPQRS సమాంతర చతుర్భుజంలో `1/2/_P + 1/2 /_Q`=
View SolutionABC సమబాహు త్రిభుజ భుజము 10 సెంమీ అయిన, వాటి భుజాల మధ్య బిందువులను కలపగ ఏర్పడు త్రిభుజ చుట్టుకొలత
View Solutionచతుర్భుజపు ఎదుటి భుజాలు _____ను కల్గి ఉంటాయి
View Solutionచతుర్భుజపు ఆసన్న భుజాలు _____ను కల్గి ఉంటాయి
View Solutionదీనిలో ఎదుటి కోణాల కర్ణాలు తప్పక ఖండించుకుంటాయి.
View Solutionరెండు కర్ణాలు సమానంగా వుండునది
View Solutionదీని భుజల మధ్య బిందువులను కలుపుట ద్వారా రాంబస్ ఏర్పడును
View SolutionABCD సమాంతర చతుర్భుజంలో `/_DAB=75^@ మరియు /_DBC = 60^@` అయిన `/_BDC` =
View SolutionABCD చతుర్భుజంలో `/_A + /_C` విలువ `./_B + /_D` కు 2 రెట్లయిన, `/_A= 40^@` ,∠D=60° అయిన `/_B`=
View Solutionరాంబస్ ABCD లో `/_ACB=40^@` అయిన `/_ADB`=
View SolutionABCD సమాంతర చతుర్భుజంలో కర్ణాలు 'O' వద్ద ఖండించుకొనును. `/_BOC=90^@` మరియు `/_BDC=50^@` అయిన `/_OAB`=
View Solutionచతుర్భుజం ABCD యొక్క కర్ణాలు ఖండించుకొనుచు, `/_A=45^@` అయిన `/_B`=
View Solution`Delta ABC` లో AD మధ్య బిందువు E,BE ని పొడిగించగా అది AC ని F వద్ద ఖండించుకొనేను. AC=10.5 సెంమీ అయిన AF విలువ
View Solutionసరైన ఎంపికతో జతపరుచుము.

View Solutionరాంబస్ యొక్క రెండు అంతరకోణాల సమద్విఖండన రేఖలు _____ఏర్పరుస్తాయి
View Solutionకర్ణాలు దీనిలో సమానము
View SolutionABCD సమాంతర చతుర్భుజంలో, /_BAD=65^@` అయిన `/_ADC`=
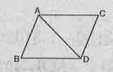
View SolutionABCD సమాంతర చతుర్భుజంలో /_A మరియు /_B త్రికోణ సమద్విఖండన రేఖలు 'O' వద్ద ఖండించుకున్న 'x' విలువ
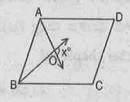
View Solution`square ABCD` లో AB=DC మరియు AD=BC, `/_A = 90^@` అయిన `square ABCD` ఒక
View Solutionఒక సమాంతర చతుర్భుజంలో కొనలన్నీ లంబలైన అది ఒక _____
View Solutionసమాంతర చతుర్భుజ విషయంలో సరైన ప్రవచనం
View Solutionకింది వాటిలో సరికానిది ఏది?
View Solutionసమాంతర చతుర్భుజపు సమద్వి ఖండన రేఖలు దీనిని ఏర్పరుచును.
View Solutionసమాంతర చతుర్భుజంలోని వరుస కోణాల నిష్పత్తి 1:2 అయిన గరిష్ట కోణము విలువ
View Solutionపటంలో `AC _|_ BD` మరియు `AC != BD` అయిన ABCD ఒక _______
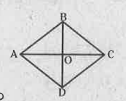
View Solutionకింది ఏ చతుర్భుజం , రాంబస్ కాదు?
View Solutionచతుర్భుజంలోని కోణాల మొత్తము_____లంబ కోణాలు
View Solutionఎదుటి భుజాల కొలతలు సమాంతరంగా గల చతుర్భుజం
View Solution`square ABCD` ఒక సమాంతర చతుర్భుజం , `/_D=80^@` అయిన `/_A,/_B,/_C` విలువలు
View Solutionరాంబస్ యొక్క కర్ణాల మధ్య గల కోణము____కోణము
View Solutionధీర్ఘచతురస్రము యొక్క ప్రతికోణము____కోణం
View Solutionచతుర్భుజ కర్ణాలు ఒక దనికోకటి సమద్విఖండన చేసుకొనిన అది ఒక
View Solutionఎదుటి కోణాల జతలు సమానముగా గలది
View Solutionధీర్ఘ చతురస్ర భుజాల మధ్య బిందువులను కలుపుట వలన ఏర్పడు పటము
View Solutionరాంబస్ యొక్క మిధ్య బిందువులను కలుపుట వలన ఏర్పడు పటము
View Solutionచతుర్భుజంలోని 4 కోణాల మొత్తము_____లంబ కోణాలు
View SolutionABCD చతుర్భుజం యొక్క ఒక కర్ణం
View Solutionఒక జత ఎదుటి భుజాలు సమానంగా గలది
View Solutionసమాంతర చతుర్భుజంలోని కర్ణము దానిని____త్రిభుజాలుగా విభజించును.
View Solutionసమానముగా వుంది లంబంగా వుండునటువంటి కర్ణాలు కల్గిన చతుర్భుజము
View Solutionదత్తపటం ABCD ఒక సమాంతర చతుర్భుజం మరియు కర్ణాలు 'O' వద్ద ఖండించుకొనిన
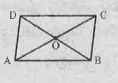
View Solutionపటంలో `/_D`=
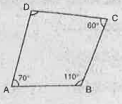
View Solution`square ABCD` ట్రెపీజియం లో`AB // CD . `/_A=45^@` అయిన `/_D`=
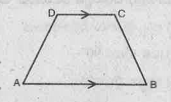
View Solution`square ABCD`సమాంతర చతుర్భుజం మరియు BC ని పొడిగించిన , `/_A=40^@` అయిన `/_DCE`=
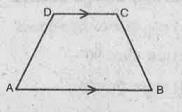
View Solution`Delta ABC` లో BC=8 సెంమీ మరియు D,E లు AB మరియు AC ల మధ్య బిందువులు , AF= `1/2 AD, AG= 1/2 AE` అయిన FG=
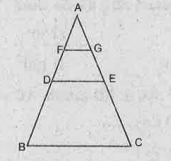
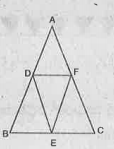
View Solution`Delta ABC` లో D,E లు మరియు F లు భుజాల మధ్య బిందువులైన `Delta DEF`=
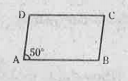
View SolutionABCD సమాంతర చతుర్భుజంలో `/_DAB=50^@` అయిన `/_ABC`=
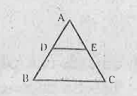
View Solution`Delta ABC` ఒక సమబాహు త్రిభుజం D,E లు AB మరియు AC ల మధ్య బిందువులైన DE=3 సెంమీ అయిన `Delta ABC` చుట్టుకొలత.
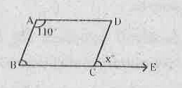
View SolutionABCD సమాంతర చతుర్భుజం, `/_BAD=110^@`, అయిన `/_DCE`=
View Solution
Exercise questions and complete solutions for chapter చతుర్భుజాలు of VGS MATHS (TELUGU) of Class 9