Complete Solutions to Exercise of chapter వైశాల్యాలు of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | వైశాల్యాలు |
| VGS PUBLICATION-BRILLIANT(TELUGU) | Exercise |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
`/_\ABC` లో `/_ABC=90^@`, `AD=DC`, `AB=12` సెం.మీ. మరియు `BC=6.5` సెం.మీ. అయిన `/_\ADB` వైశాల్యము కనుగొనండి.
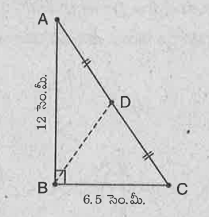
View SolutionPQRS చతుర్భుజములో `/_QPS=/_SQR=90^@`, `PQ=12` సెం.మీ.,`PS=9` సెం.మీ. `QR=8` సెం.మీ మరియు `SR=17` సెం.మీ. అయిన PQRS వైశాల్యం కనుగొనండి. (సూచనా: PQRS లో రెండు భాగాలున్నాయి.)
View Solutionకింది పటములో ADCE ఒక దీర్ఘ చతురస్రాము అయిన ABCD ట్రెపీజియం వైశాల్యము కనుగొనండి. (సూచన: ABCD లో రెండు భాగాలున్నాయి.)
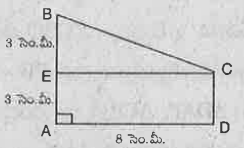
View SolutionABCD ఒక సమాంతర చతుర్భుజము, కర్ణములు AC మరియు BD లు `O` వద్ద ఖండించుకున్నాయి. (`/_\AOD)`వై|| =(`/_\BOC`) వై|| అని నిరూపించండి. (సూచనా: సర్వసమాన పాటలు సమన వైశాల్యాలు కలిగి ఉంటాయి.
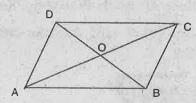
View SolutionABCD సమాంతర చతుభుజ వైశాల్యము 36 చ. సెం.మీ `AB=4.2` సెం.మీ. అయిన ABEF సమాంతర చతుర్భుజము కనుగొనుము.
View SolutionABCD ఒక సమాంతర చతుర్భుజము. DC భుజము పైకి గీయబడిన లంబము AE మరియు AD భుజము పైకి గీయబడిన లాభము CF. `AB=10`సెం.మీ., `AE=8` సెం.మీ.,`CF=12` మరియు సెం.మీ అయిన AD కొలత కనుగొనుము.
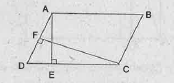
View SolutionABCD చతుర్భుజంలో AD=BC మరియు `/_DAB = /_CBA` అయిన BD=AC
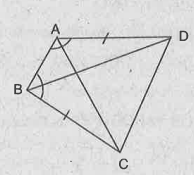
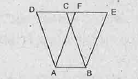
View Solution`/_\APM`, `/_\DPO`, `/_\OCN` మరియు `/_\MNB` లను ఒక చోట చేర్చితే ఏ రకమైన చతుర్భుజం వస్తుంది?
View SolutionABCD సమాంతర చతుర్భుజములో P మరియు Q అను రెండు బిందువులు వరుసగా DC మరియు AD లాపై ఉంటె `(/_\APB)`వై||=`(/_\BQC)` వై|| అని చూపండి.
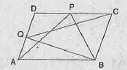
View SolutionABCD సమాంతర చతుర్భుజము అంతరములో P అనేది ఒక బిందువు అయిన కింది వానిని నిరూపించండి.
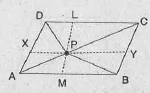
`(/_\APB)` వై\\+ `(/_\PCD)`వై||= `1/2(ABCD)` వై||
View SolutionABCD సమాంతర చతుర్భుజము అంతరములో P అనేది ఒక బిందువు అయిన కింది వానిని నిరూపించండి.
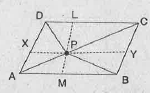
`(/_\APD)` వై\\+ `(/_\PBC)`వై||= `(/_\APB)` వై|| +`(/_\PCD)`వై||(సూచన: AB కి సమాంతరంగా P నుండి ఒక రేఖను గీయుము.)
View Solutionట్రెపీజియం యొక్క వైశాల్యము దాని సమాంతర భుజాల మొత్తాన్ని వాటి మధ్య దూరంలో గుణించగా వచ్చే లంబంలో సగము ఉంటుంది అని నిరూపించండి.
View SolutionPQRS మరియు ABRS అనేవి రెండు సమాంతర చతుర్భుజాలు. BR భుజముపై X అనేది ఒక బిందువు అయిన
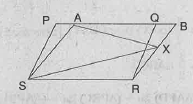
(PQRS)వై|| =(ABRS) వై||
View SolutionPQRS మరియు ABRS అనేవి రెండు సమాంతర చతుర్భుజాలు. BR భుజముపై X అనేది ఒక బిందువు అయిన
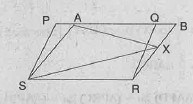
`(/_\AXS)`వై||=`1/2(PQRS)` వై||
View Solutionఒక రైతు పటంలో చూపినట్లు PQRS సమాంతర చతుర్భుజ ఆకారములో పొలము ఉన్నది. భుజముపై మద్య బిందువు A నుండి P,Q బిందువులను కలిపారు. పొలము ఎన్ని భాగాలుగా విభజించబడినది? ఏ భాగాలూ ఏ ఆకారములో ఉన్నాయి? రైతు తన పొలములో వారి మరియు వేరుశెనగ పంటను సమన భాగాలలో వేయాలనుకుంటే, ఏ విధంగా వేస్తాడు? కారణాలు తెలపండి.
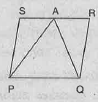
View Solutionరాంబస్ యొక్క వైశాల్యము, దాని కర్ణముల లంబము లో సగం ఉంటుందని నిరూపించండి.
View Solution`/_\ABC` లో (పటం చుడండి), మధ్య గత రేఖ AD యొక్క మధ్య బిందువు E అయిన
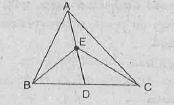 `/_\ABE`వై||=`/_\ACE` వై||
`/_\ABE`వై||=`/_\ACE` వై||
View Solution`/_\ABC` లో (పటం చుడండి), మధ్య గత రేఖ AD యొక్క మధ్య బిందువు E అయిన
 `/_\ABE`వై||=`/_\ACE` వై||
`/_\ABE`వై||=`/_\ACE` వై||
View Solutionసమాంతర చతుర్భుజములో కారణాలు, దానిని సమన వైశాల్యము గల నాలుగు త్రిభుజాలుగా విభజిస్తాయని చూపండి.
View Solutionపటంలో త్రిభుజాలు `/_\ABC` మరియు `/_\ABD` ఒకే భూమి AB పైన ఉన్నాయి. CD రేఖ ఖండం overline(AB) ని O వద్ద సమద్వి ఖండన చేస్తే `(/_\ABC)`వై||=`(/_\ABD)` వై|| అని చూపండి.
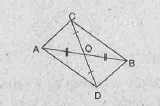
View Solutionపటంలో చూపిన విధానంగా `/_\ ABC` లో D,E,F లు వరుసగా భుజాలు BC,CA మరియు AB యొక్క మధ్య బిందువులు అయినా కింది వానిని నిరూపించండి.
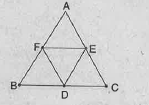
BDEF ఒక సమాంతర చతుర్భుజము
View Solutionపటంలో చూపిన విధానంగా `/_\ ABC` లో D,E,F లు వరుసగా భుజాలు BC,CA మరియు AB యొక్క మధ్య బిందువులు అయినా కింది వానిని నిరూపించండి.
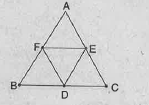
`(/_\DEF)`వై||=`1/4(/_\ABC)`వై||
View Solutionపటంలో చూపిన విధానంగా `/_\ ABC` లో D,E,F లు వరుసగా భుజాలు BC,CA మరియు AB యొక్క మధ్య బిందువులు అయినా కింది వానిని నిరూపించండి.
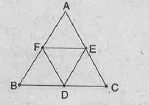 (BDEF)వై||=`1/2 (/_\ABC)`వై||
(BDEF)వై||=`1/2 (/_\ABC)`వై||
View Solutionఈ క్రింది పటాలలో `DE |\| BC` EC ని కనుగొనుము.
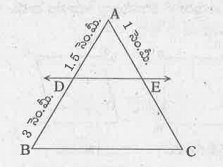
View Solutionకింది పటంలో BC కు సమాంతరంగా A గుండా XY అనే రేఖ గీయబడింది. BE||CA మరియు CF||BA లను గిస్తే అవి XY ను E మరియు F ల వద్ద వరుసగా ఖండిస్తే `(/_\ABE)` వై||= `(/_\ACF)` వై|| అని చూపండి.
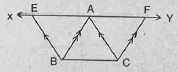
View Solutionకింది పటంలో ABCD ట్రెపీజియంలో AB//DC కర్ణాలు AC మరియు BD లు `O` వద్ద ఖండించుకున్నాయి, `(/_\AOD)`వై||=`(/_\BOC)` వై|| అని చూపండి.
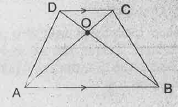
View Solutionకింది పటంలో ABCDE ఒక పంచభుజి. B గుండా AC కు సమాంతరంగా గీచిన రేఖ, పొడిగించిన DC ని F వద్ద ఖండించిన కింది వానిని నిరూపించుము. `(/_\ACB)`వై||=`(/_\ACF)`వై||
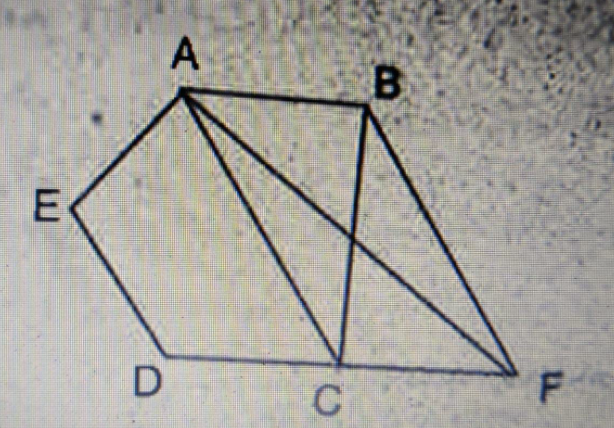
View Solutionకింది పటంలో ABCDE ఒక పంచభుజి. B గుండా AC కు సమాంతరంగా గీచిన రేఖ, పొడిగించిన DC ని F వద్ద ఖండించిన కింది వానిని నిరూపించుము. `(/_\ACB)`వై||=`(/_\ACF)`వై||

View Solutionకింది పటంలో `/_\RAS` వై||=`/_\RBS` వై|| మరియు `/_\QRB` వై=`/_\PAS` వై|| అయిన చతుర్భుజాలు PQSR మరియు RSBAలో రెండును ట్రెపీజియం లని చూపండి.
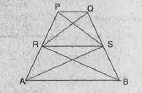
View Solutionఒక గ్రామంలో రమ్మయ్య అనే వ్యక్తికీ చతుర్భుజాకారంలో కాళీ స్థలం కలదు. ఆ గ్రామ పంచాయతీ లో పాఠశాల నిర్మాణానికి అతని స్థలం లో ఒక ముళ్లలో కొంత భాగం కావాల్సి వచ్చింది. ఆయన స్థలాన్ని ఇవ్వడానికి అంగీకరిస్తూ, దానికి బదులుగా అంటే వైశాల్యం గల స్థలాన్ని పొందితే ఏ విధంగా ఆ స్థలం వస్తుందో వివరించండి. (స్థలం యొక్క చిత్తూ పాఠం గీయండి.)
View Solutionఒక సమాంతర చతుర్భుజం యొక్క వైశాల్యముల లబ్దము..... ()
View Solutionఒక త్రిభుజం మరియు సమన్తరా చతుర్భుజాలు ఒకే భూమి ఒకే జత సమంతరాలు మధ్యనున్నట్లయితే త్రిభుజా వైశాల్యం సమాంతర చతుర్భుజ వైశాల్యమునకు ...... ఉందును. ( )
View Solutionరెండు త్రిభుజాల వైశాల్యాలు సమానమైన అవి సరూపాలు ( )
View Solutionవైశాలయంను... యూనిట్లు తెలియజేస్తారు. ( )
View SolutionA,B,C లు సరేఖియులైన `/_\ABC` వైశాల్యము=
View Solutionరెండు సర్వసమాన పాటలు వైశాల్యములు..... ( )
View Solutionఒక సెం.మీ 2.5 మీ. లను తెలియచేసిన, ఒక చతురస్రవు వైశాల్యము 10 మీ^2 . అయినా దానిని సూచించు సెం.మీ. విలువ........ ( )
View Solutionపటం నుండి ∆ABC వైశాల్యం.........( )
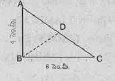
View Solutionపటం ABCDE యొక్క వైశాల్యము ( )
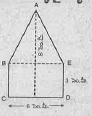
View Solutionసమాంతర చతుర్భుజం పటం ABCD లో `/_\`AOD వైశాల్యము ( )
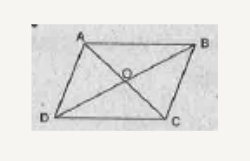
View Solutionపటంలో AB//CF అయిన `squareABCD` = ( )
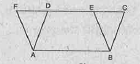
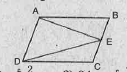
View Solutionకింది పటంలో `/_\`ADE `వైశాల్యం 24 సెం.మీ^2` `అయిన `squareABCD` వైశాల్యము ( )
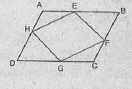
View Solution`squareABCD` సమాంతర చతుర్భుజపు భుజాలు మధ్య బిందువులు E,F,G మరియు H అయిన `/_\AEH +/_\BEF +/_\CGF +/_\DGH` ( )
View Solutionఒక బహుభుజని విభజించిన ఏర్పడు ప్రతము ఆకారం.... ( )
View Solutionఒకే భూమిపై గల రెండు త్రిభుజాల వైశాల్యాలు సమానమైన అవి....... మధ్య ఉంటాయి.
View Solution"ఒకే భూమి మరియు ఒకే సమాంతర రేఖల మధ్య గల రెండు సమాంతర చతుర్భుజల వైశాల్యాలు సమానము" అని చూపండి.
View Solution
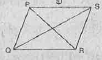
square PQRS సమాంతర చతుర్భుజం లో `/_\ PQR` వైశాల్యం......
View Solutionచతురస్రం యొక్క కర్ణం 6 సెంటీమీటర్లు అయిన దాని చుట్టుకొలత ఎంత ?
View Solutionరాంబస్ వైశాల్యము కు సూత్రము........
View Solutionఒక రాంబస్ కర్ణాలు 4 సెం.మీ. మరియు 6 సెం.మీ అయిన దాని వైశాల్యము.........
View Solution
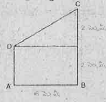
పై పటం యొక్క వైశాల్యము.....
View Solution`1 మీ.^2` =............. `సెం.మీ^2`
View Solution
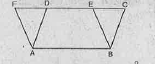 `squareABCD` వైశాల్యం= 72 సెం.మీ^2 అయిన `square ABEF` వైశాల్యం=.......
`squareABCD` వైశాల్యం= 72 సెం.మీ^2 అయిన `square ABEF` వైశాల్యం=.......
View Solutionఒక సమాంతర చతుర్భుజము యొక్క భూమి 16 సెం.మీ. మరియు వైశాల్యం 64 చ.సెం.మీ . అయిన దాని ఎత్తు........
View Solution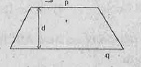 పై పటంలో చూపబడిన ట్రెపీజియం వైశాల్యం ..... చ.యూ.
పై పటంలో చూపబడిన ట్రెపీజియం వైశాల్యం ..... చ.యూ.
View Solution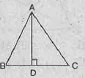 `/_\ADC` వైశాల్యము= `14.5సెం.మీ` మరియు BC పై AD మధ్యగతరేఖ అయిన `/_\ABC`వై||=........
`/_\ADC` వైశాల్యము= `14.5సెం.మీ` మరియు BC పై AD మధ్యగతరేఖ అయిన `/_\ABC`వై||=........
View Solution
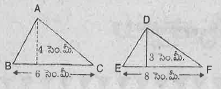 `/_\ABC~=/_\DEF` ఆగునా?....
`/_\ABC~=/_\DEF` ఆగునా?....
View Solutionరాంబస్ యొక్క వైశాల్యం 27 చ.యూ. కర్ణము BD= 6 సెం.మీ. అయిన మరొక కర్ణము AC విలువ...........
View Solutionజతపర్చుము.
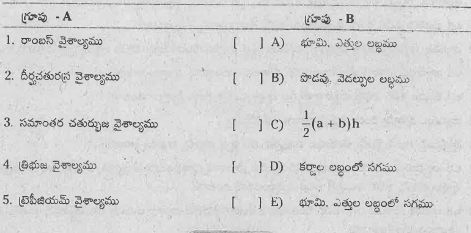
View Solution
Exercise questions and complete solutions for chapter వైశాల్యాలు of VGS MATHS (TELUGU) of Class 9