रचनाएँ कक्षा 10 गणित
भूमिका
कक्षा IX में एक रूलर (पटरी) और एक परकार (compass) का प्रयोग कर कुछ रचनाएँ, जैसे एक कोण को समद्विभाजित करना, एक रेखाखंड को लम्बवत समद्विभाजित करना, इत्यादि हम बना चुके हैं। वहाँ त्रिभुज के 6 भागों (तीन भुजाएँ एवं तीन कोणों) में से किन्हीं तीन के ज्ञात रहने पर हम त्रिभुज की रचना करना जान चुके हैं। इस अध्याय में हम आधारभूत अनुपातिकता प्रमेय पर आधारित कुछ रचनाएँ करेंगे। साथ ही किसी वृत्त के किसी बिन्दु पर या वृत्त के बाहर के किसी बिन्दु से, वृत्त की स्पर्श रेखा भी खींचेंगे।
आइये जानते है, रचनाएँ को और करीब से ...
हमने कक्षा IX में, एक पटरी तथा परकार का प्रयोग करके कुछ रचनाएँ की थी।
अब इस अध्याय में, हम पिछली रचनाओं के ज्ञान का उपयोग करते हुए, एक रेखाखंड को दिए हुए अनुपात में विभाजित करना, एक दिए गए स्केल गुणक के अनुसार दिए गए त्रिभुज के समरूप एक त्रिभुज की रचना करना तथा एक वृत्त के बाहर स्थित एक बिंदु से उस पर स्पर्श रेखाओं की रचना करना सीखेंगे।
रेखाखंड का विभाजन
मान लो कि एक रेखाखंड दिया है और हमको उसे एक दिए गए अनुपात में विभाजित करना है, माना रेखा को 3:2 में विभाजित करना है। अतः इसकी लंबाई माप कर तथा दिए गए अनुपात के अनुसार एक बिंदु चिह्नित कर सकते हैं।
परंतु यदि हमारे पास इसे सही-सही मापने की कोई विधि न हो, तो हम इस बिंदु को कैसे प्राप्त करेंगे?
इस बिंदु को प्राप्त करने के लिए, हम निम्नलिखित दो विधियों पर चर्चा करेंगे:
रचना 11.1
एक रेखाखंड को दिए हुए अनुपात में विभाजित करना।
इस रचना को समझने के लिए मान लेते है, एक रेखाखंड AB है जिसे हमे m:n में विभाजित करना है, जहाँ m=3 तथा n=2 मान लेते है।
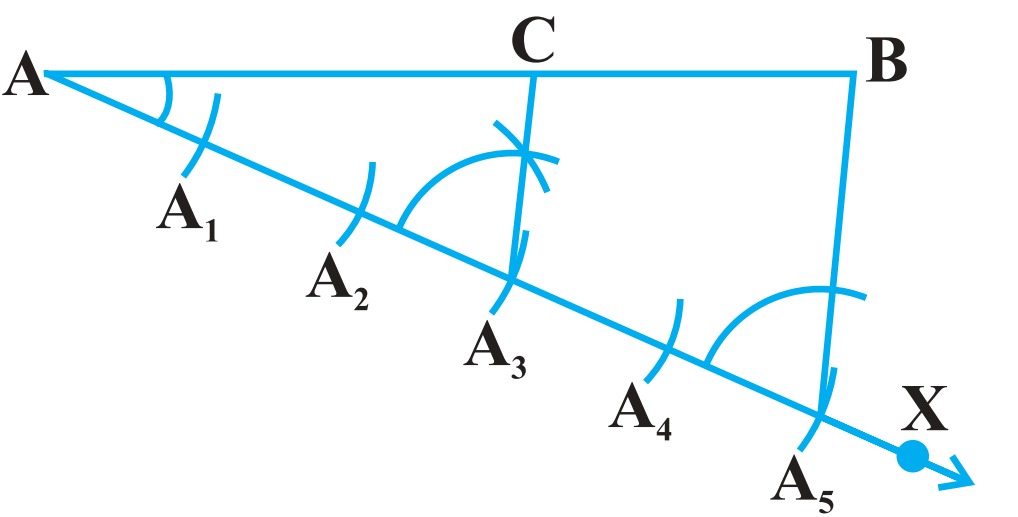
रचना के चरण:
चरण 1: सबसे पहले AB से एक न्यूनकोण बनाती हुई किरण AX खींचिए।
चरण 2: अब AX किरण पर (m+n =3+2=5) 5 बिन्दु A1,A2,A3,A4 तथा A5 इस प्रकार से चिन्हित करो की AA1=A1A2=A2A3=A3A4=A4A5 हो।
चरण 3: अब BA5 को मिलाइए।
चरण 4: अब BA5 के समांतर एक रेखा बिन्दु A3 (क्योंकि m=3 इसलिए बिन्दु A3 लिया है) से खींचिए जो रेखा AB को बिन्दु C पर मिलता है।
इसी के साथ हमारी रचना पूरी होती है, रेखा AB, AC व CB में विभाजित हुई हैं, जहाँ AC:CB=3:2
चित्र में देख सकते हैं कि AA5B एक त्रिभुज हैं, जिसमे इसकी एक भुजा A5B के समांतर एक रेखा A3C खींची गई है, तब :
आधारभूत समानुपातिकता प्रमेय द्वारा
AA3A3A5=ACCB
और रचना से हम देख सकते है:
AA3A3A5=32
तब
ACCB=32
अतः ये निष्कर्ष निकलता हैं, कि बिन्दु C रेखा AB को 3:2 के अनुपात में विभाजित करता है।
वैकल्पिक विधि
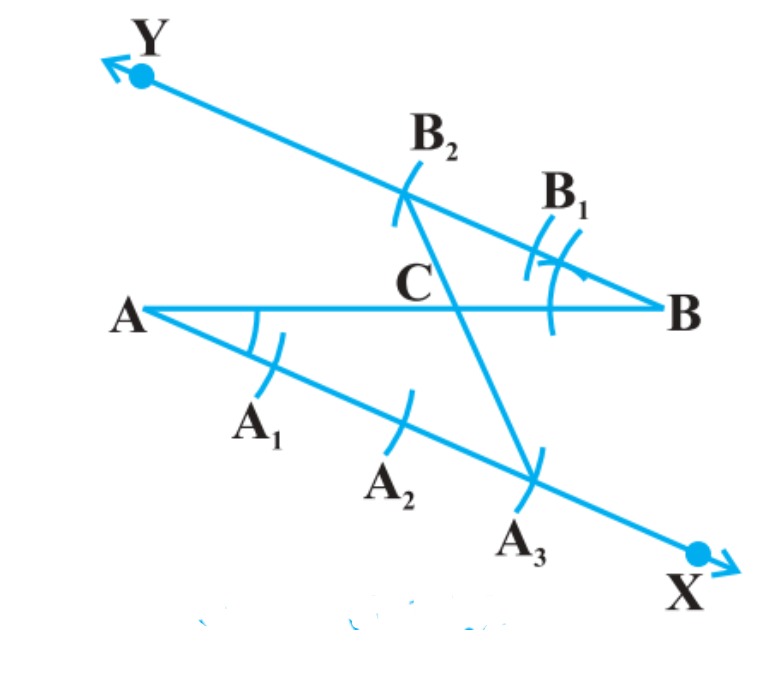
रचना के चरण:
चरण 1: AB से न्यूनकोण बनाती कोई किरण AX खींचिए।
चरण 2: ∠BAX के बराबर ∠ABY बनाकर AX के समांतर एक किरण BY खींचिए।
चरण 3: AX पर बिंदु A1,A2,A3 (m=3) और BY पर बिंदु B1,B2 (n=2) इस प्रकार अंकित कीजिए कि
AA1=A1A2=A2A3=BB1=B1B2 हो।
चरण 4: A3B2 को मिलाइए। माना यह AB को बिंदु C पर प्रतिच्छेद करती है।
तब, AC:CB=3:2 है।
यहाँ △AA3C ~△B2BC
AA3BB2=ACBC
परंतु रचना द्वारा AA3BB2=32
अतः, ACBC=32
वास्तव में इन विधियों द्वारा दिये गये रेखाखंड को किसी भी अनुपात में विभाजित किया जा सकता है।
अब हम ऊपर दी गई रचना को एक दिए गए त्रिभुज के समरूप एक अन्य त्रिभुज की रचना करने में उपयोग करेंगे जिसकी भुजाओं और दिए गए त्रिभुज की संगत भुजाओं में एक अनुपात दिया हुआ हो।
उदाहरण 1
एक 7.8 सेमी लंबी रेखा को 5:8 के अनुपात में अन्त: विभाजित कीजिए।
दिया हैं, एक 7.8 सेमी लंबी रेखा को 5:8 के अनुपात विभाजित करना हैं।
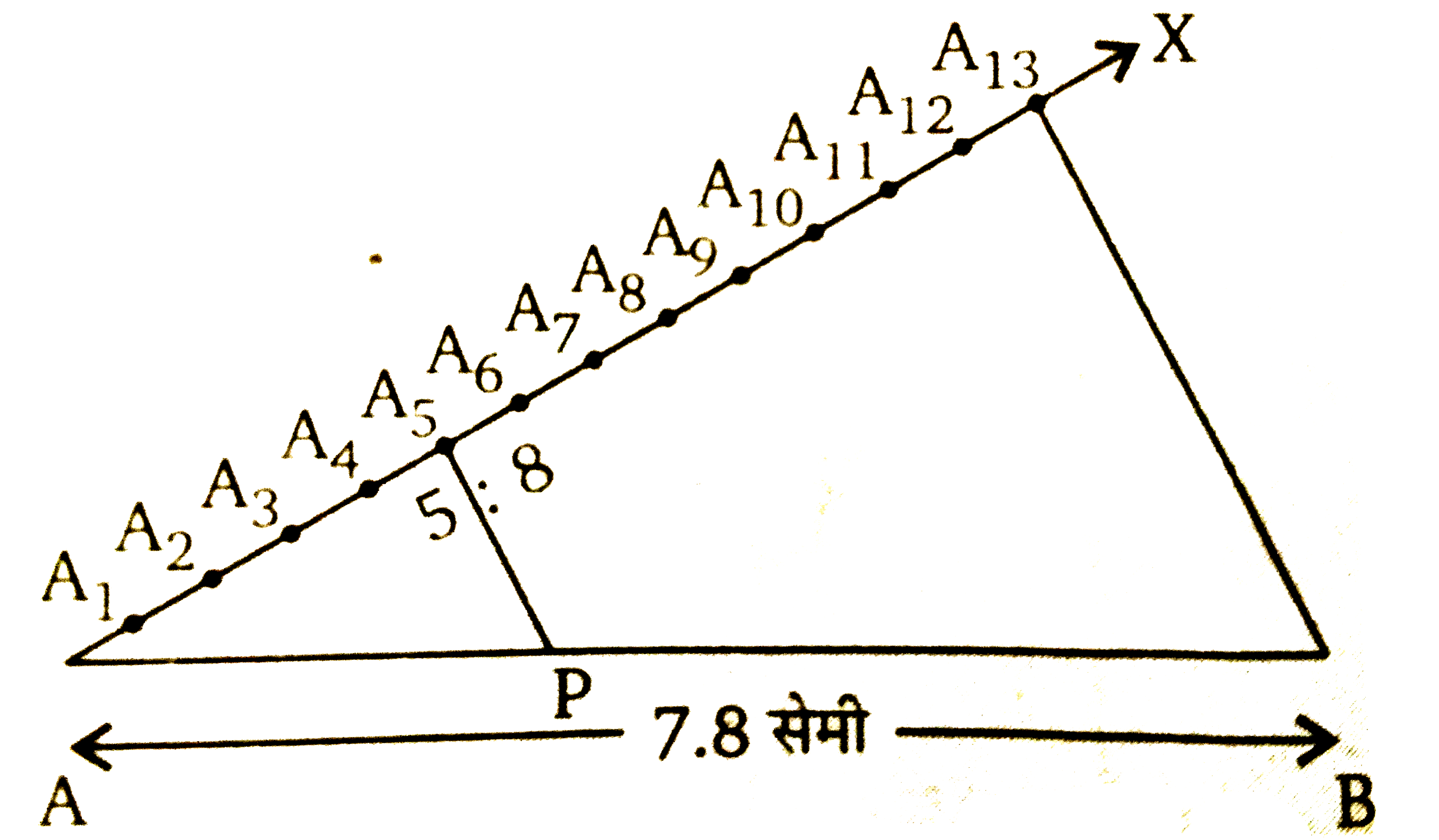
रचना के चरण :
चरण 1: AB=7.8 सेमी का एक रेखाखंड खींचिए।
चरण 2: AB से न्यूनकोण बनाती हुई एक किरण AX खींचिए।
चरण 3: AX दिशा में (5+8=13)13 बिन्दुओं A1,A2,A3,A4....A11,A12,A13 को इस प्रकार चिन्हित कीजिए कि
AA1=A1A2=.........=A12A13 हो।
चरण 4: A13B को मिलाइए।
चरण 5: बिंदु A5 से होते हुए तथा रेखाखंड A13B के समान्तर एक रेखाखंड खींचे, जो AB को बिंदु P पर मिलता है।
तब P, AB पर बिन्दु है जो इसे 5:8 के अनुपात में अन्तः विभाजित करता है।
उत्पत्ति: रचना से हम देख सकते है
A5P||A13B
आधारभूत समानुपातिकता प्रमेय द्वारा
⇒APPB=AA5A5A13=58
अतः निष्कर्ष निकलता हैं, कि बिन्दु P, AB को 5:8 के अनुपात में अन्त: विभाजित करता है।
उदाहरण 2
एक बिंदु ज्ञात कीजिए जो 7 सेमी के रेखाखंड को 2:3 के अनुपात में अन्तः विभाजित करता हैं।
दिया हैं, एक 7 सेमी लंबी रेखा को 2:3 के अनुपात विभाजित करना हैं।

रचना के चरण
चरण 1: AB=7 सेमी का एक रेखाखंड खींचिए।
चरण 2: AB से न्यूनकोण ∠BAC बनाती एक किरण खींचिए।
चरण 3: AC पर (2+3)=5 बिंदु A1,A2,A3,A4 और A5 इस प्रकार अंकित करते हैं कि
AA1=A1A2=A2A3=A3A4=A4A5 हो।
चरण 4: BA5 को मिलाइए।
चरण 5: बिंदु A2 से होते हुए तथा रेखाखंड A5B के समान्तर एक रेखाखंड खींचिए जो AB को बिंदु P पर मिलता है। तब P, AB पर बिन्दु है जो इसे 2:3 के अनुपात में अन्तः विभाजित करता है।
उत्पत्ति: ΔAA5B में,
A2P||A5B (रचना से)
∴AA2A2A5=APPB (आधारभूत समानुपातिकता प्रमेय द्वारा)
⇒23=APPB
⇒AP:PB=2:3
अर्थात् P, AB को 2:3 के अनुपात में अन्तः विभाजित करता हैं।
रचना 11.2
एक दिए गए स्केल गुणक के अनुसार दिए गए त्रिभुज के समरूप एक त्रिभुज की रचना करना।
इस रचना की दो स्थितियाँ हैं। एक में, जिस त्रिभुज की रचना करनी है, वह दिए गए त्रिभुज से छोटा हो तथा दूसरी में वह बड़ा हो। यहाँ स्केल गुणक का अर्थ रचना करने वाले त्रिभुज की भुजाओं तथा दिए हुए त्रिभुज की संगत भुजाओं के अनुपात से है।
यही विधि व्यापक स्थिति में भी लागू होगी। इसे हम निम्न उदाहरणों से समझेंगे:
उदाहरण 3
एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए। जिसकी, भुजाएँ दिए गए त्रिभुज की संगत भुजाओं की 34 हो।
ΔABC दिया हुआ है एक अन्य त्रिभुज की रचना करनी है जिसकी, भुजाएँ त्रिभुज ABC की संगत भुजाओं की 34 हो।
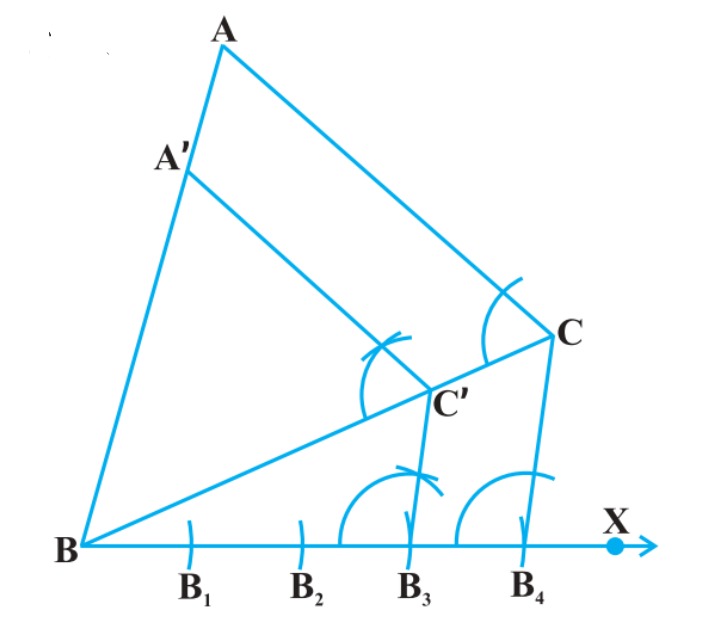
रचना के चरण:
चरण 1: सर्वप्रथम दी हुई नापो से ΔABC बनाए तथा BC से शीर्ष A की दूसरी ओर न्यूनकोण बनाती हुई एक किरण BX खींचिए।
चरण 2: BX पर 4 बिंदु B1,B2,B3 तथा B4 इस प्रकार अंकित कीजिए कि BB1=B1B2=B2B3=B3B4 हो।
चरण 3: B4C को मिलाइए और बिंदु B3 से होकर जाने वाली B4C के समांतर एक रेखा BC को C' पर प्रतिच्छेद करती हुई खींचिए।
चरण 4: अब C' से होकर जाने वाली CA के समांतर एक रेखा BA को A' पर प्रतिच्छेद करती हुई खींचिए।
चरण 5: अतः ΔA'BC' अभीष्ट त्रिभुज है।
उत्पत्ति: आइए देखें कि इस रचना से कैसे अभीष्ट त्रिभुज प्राप्त हो जाता है।
रचना 11.1 से, BC'C'C=31
इसलिए BCBC'=BC'+C'CBC'
=1+C'CBC'
=1+13=43
साथ ही, C'A', CA के समांतर है। इसलिए ΔA'BC' ~ ΔABC
अतः A'BAB=A'C'AC=BC'BC=34
उदाहरण 4
एक ΔABC बनाये जिसमे BC=5 सेमी, CA=6 सेमी तथा AB=7 सेमी, ΔABC के समरूप एक त्रिभुज बनाये जिसकी, भुजाएँ ΔABC की संगत भुजाओं की 75 गुनी है।
ΔABC दिया हुआ है एक अन्य त्रिभुज की रचना करनी है जिसकी, भुजाएँ त्रिभुज ABC की संगत भुजाओं की 75 गुनी हो।
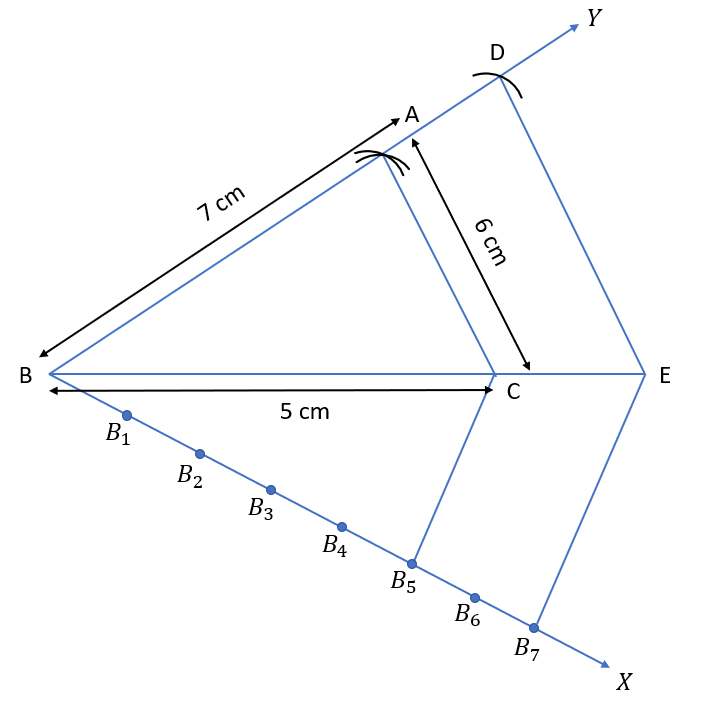
रचना के चरण:
चरण 1: एक रेखाखंड BC=5 सेमी खींचे।
चरण 2: B और C को केन्द्र मानकर क्रमशः 7 सेमी और 6 सेमी त्रिज्या के चाप बनाए। जो एक - दूसरे को बिन्दु A पर काटे।
चरण 3: BA और CA को मिला दे। इस तरह ΔABC प्राप्त हुआ।
चरण 4 : B से न्यूनकोण बनाते हुए नीचे की ओर किरण BX खींचे।
चरण 5: 7 बिन्दुओ B1,B2,B3,B4,B5,B6 और B7 को BX पर इस प्रकार अंकित करे कि
BB1=B1B2=B2B3=....=B6B7
चरण 6: B5C को मिला दे। B7 से E को इस प्रकार मिलाए कि
B7E || B5C हो एवं BC को E बिन्दु तक बढ़ाये।
चरण 7: बिन्दु E से ED || CA खींचे जो BA के बढ़े हुए भाग को D पर काटे।
तब, ΔDBE अभीष्ट त्रिभुज है जिसकी भुजाएँ ΔABC की भुजाओं की 75 गुनी है।
उदाहरण 5
एक त्रिभुज ABC की रचना कीजिए जिसमे AB=6.5 सेमी, ∠B=60∘ तथा BC=5.5 सेमी तथा त्रिभुज ABC के समरूप एक त्रिभुज AB'C' की भी रचना कीजिए जिसकी प्रत्येक भुजा, ΔABC की संगत भुजा की 32 गुनी है।
यहाँ AB=6.5 सेमी, ∠B=60∘ तथा BC=5.5 सेमी तथा त्रिभुज ABC के समरूप एक त्रिभुज AB'C' की भी रचना करनी हैं, जिसकी प्रत्येक भुजा, ΔABC की संगत भुजा की 32 गुनी है।

रचना के चरण :
चरण 1: AB=6.5 सेमी का एक रेखाखंड खींचिए।
चरण 2: BY की दिशा मे ∠B=60∘ खींचिए।
चरण 3: B को केंद्र मानकर एक 5.5 सेमी का एक चाप C पर काटे।
चरण 4: AC को मिला दे, तो इस तरह ΔABC प्राप्त हुआ।
चरण 5: AX पर A1,A2,A3 तीन बिन्दुओ को इस प्रकार अंकित करे कि AA1=A1A2=A2A3 हो।
चरण 6: A2 को B से मिलाए और A3B' मे मिलाए जो कि A2B के समान्तर होगा।
चरण 7: AC को आगे C' तक बढ़ाते हैं तथा B' को C' से मिलाते हैं जो की BC के समांतर हैं।
तब, ΔAB'C' अभीष्ट त्रिभुज है।
किसी वृत्त पर स्पर्श रेखा की रचना
बच्चों हम वृत्त अध्याय में पढ़ चुके हैं कि यदि कोई बिंदु वृत्त के अंदर स्थित है, तो इस बिंदु से जाने वाली वृत्त की कोई स्पर्श रेखा नहीं हो सकती है। परंतु यदि बिंदु वृत्त पर स्थित है, तो उस बिंदु पर वृत्त की एक और केवल एक स्पर्श रेखा हो सकती है, जो उस बिंदु से जाने वाली त्रिज्या पर लंब होती है। अत: यदि आप वृत्त के किसी बिंदु पर स्पर्श रेखा खींचना चाहते हैं, तो केवल उस बिंदु से जाने वाली त्रिज्या खींचिए और उसी बिंदु पर त्रिज्या की लंब रेखा खींचिए तो, यही अभीष्ट स्पर्श रेखा होगी।
बच्चों हमने यह भी देखा है कि यदि कोई बिंदु वृत्त के बाहर स्थित है, तो इस बिंदु से वृत्त पर दो स्पर्श रेखाएँ खींची जा सकती हैं। चलिए देखते हैं, कि इन स्पर्श रेखाओं की रचना कैसे की जाती है:-
रचना 11.3
एक वृत्त के बाहर स्थित एक बिंदु से उस पर स्पर्श रेखाओं की रचना करना।
बच्चों मान लेते हैं, एक O केंद्र वाले वृत्त पर एक बाह्य बिन्दु P से दो स्पर्श रेखा खींचनी हैं।
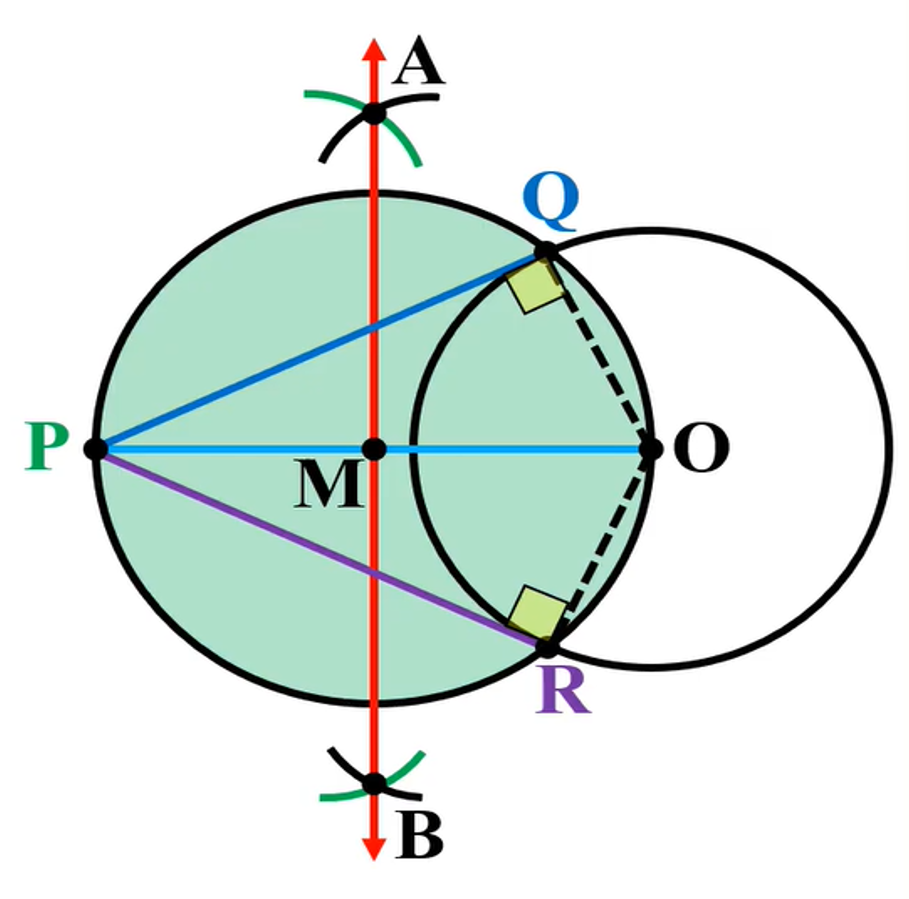
रचना के चरण
चरण 1: बच्चों सबसे पहले बिन्दु P को वृत्त के केंद्र O से मिलाकर PO खींचिए।
चरण 2: अब PO का समद्विभाजन करके इसका मध्य बिन्दु M ज्ञात कीजिए।
चरण 3: M को केंद्र मानते हुए परकार में MO त्रिज्या लेकर एक वृत्त बनाइये और मान लेते है ये वृत्त दिए गए वृत्त को Q व R पर काटता है ।
चरण 4: अंत में P से Q व R को मिलाइए तब PQ व PR अभीष्ट दो स्पर्श रेखाएँ हैं।
उत्पत्ति: OQ और OR को मिलाइए।
तब, ∠PQO तथा ∠PRO अर्धवृत्त में बना एक कोण है। चूंकि अर्धवृत्त का कोण समकोण होता हैं।
अतः, ∠PQO=90∘ तथा ∠PRO=90∘
चूंकि PQ, OQ पर लंब हैं क्योंकि, OQ दिए वृत्त की त्रिज्या है, इसलिए PQ वृत्त की स्पर्श रेखा ही होगी।
इसी प्रकार, PR भी वृत्त की स्पर्श रेखा है।
अतः PQ और PR दो स्पर्श रेखा हैं।
Note: यदि वृत्त का केंद्र नहीं दिया है, तो हम कोई दो असमांतर जीवाएँ लेकर तथा उनके लंब समद्विभाजकों के प्रतिच्छेद बिंदु के रूप में केंद्र ज्ञात कर सकते हैं। इसके बाद, उपर्युक्त रूप से आगे बढ़ सकते हैं।
उदाहरण 6
6 सेमी त्रिज्या का एक वृत्त खींचिए। केंद्र से 10 सेमी दूर स्थित एक बिंदु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और इनकी लम्बाइयाँ मापिए।
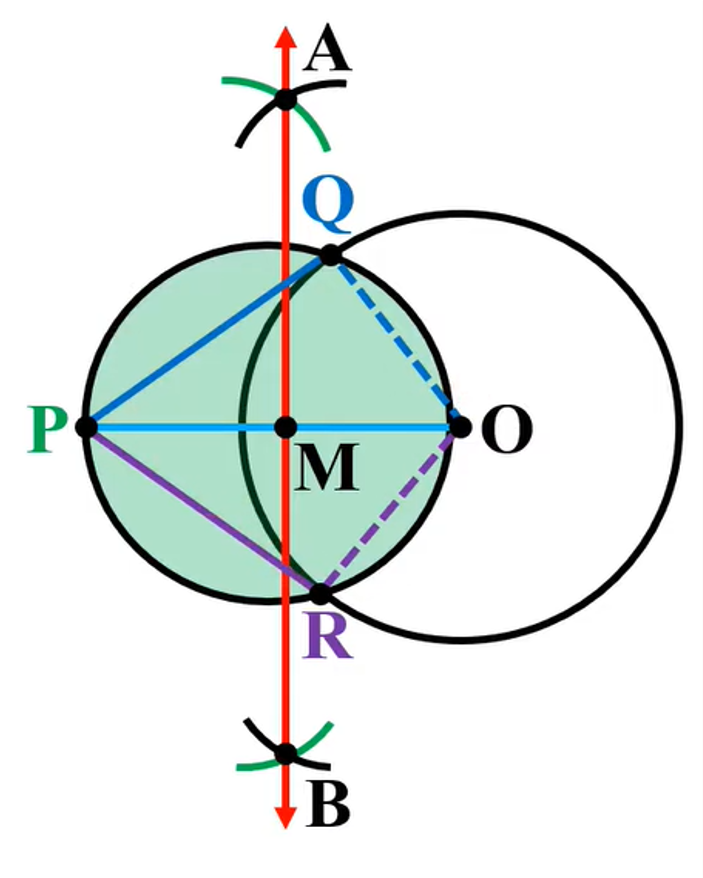
रचना के चरण
चरण 1: किसी बिंदु O को केंद्र मानकर एक 6cm त्रिज्या का वृत्त बनाया। एक बिंदु P लिया जो केंद्र O से 10cm दूर है। OP को मिलाया।
चरण 2: OP का लंब समद्विभाजक खींचा जो PO को बिंदु M पर मिलता है।
चरण 3: M को केंद्र मानकर तथा MO त्रिज्या लेकर एक वृत्त बनाया।
चरण 4: माना ये वृत्त, दिए गए वृत्त को बिन्दुओं Q और R पर कटता है।
चरण 5: P और Q तथा P और R को मिलाया। PQ और PR अभीष्ट दो स्पर्श रेखाएँ हैं।
चरण 6: PQ तथा PR प्रत्येक की लम्बाई 8cm है।
उदाहरण 7
5 सेमी त्रिज्या का एक वृत्त खींचे। वृत्त की दो स्पर्श रेखाएँ खींचिए जो आपस में 60∘ कोण पर झुकी हो।
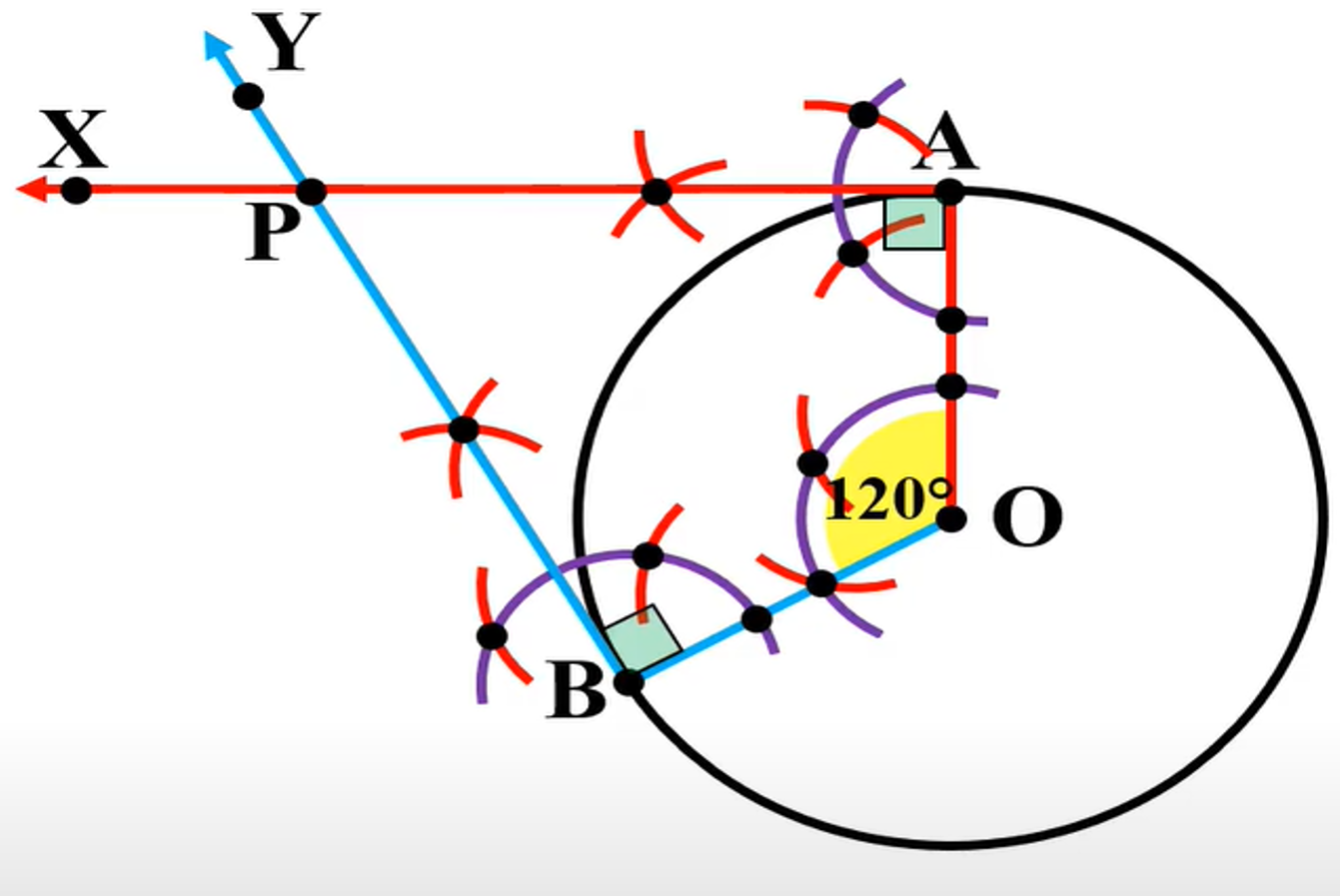
रचना के चरण
चरण 1: किसी बिंदु O को केंद्र मानकर 5cm त्रिज्या का एक वृत्त खींचिए।
चरण 2: वृत्त पर एक बिंदु A लीजिए और OA को मिलाइए।
चरण 3: OA पर 120∘ के कोण पर OB खींचिए।
चरण 4: AO पर 90∘ का कोण बनाने वाली किरण AX खींचिए।
चरण 5: BO पर 90∘ का कोण बनाने वाली किरण BY खींचिए।
चरण 6: माना कि किरण AX और BY एक दूसरे को बिन्दु P पर प्रतिच्छेद करते हैं। तब, PA और PB अभीष्ट दो स्पर्श रेखाएँ हैं, जो परस्पर 60∘ के कोण पर झुकी हैं।
उदाहरण 8
5cm त्रिज्या का एक वृत्त खींचें। इस पर P एक बिन्दु अंकित करें तथा केन्द्र का प्रयोग किये बिना बिन्दु P पर वृत्त की एक स्पर्श रेखा खींचे।
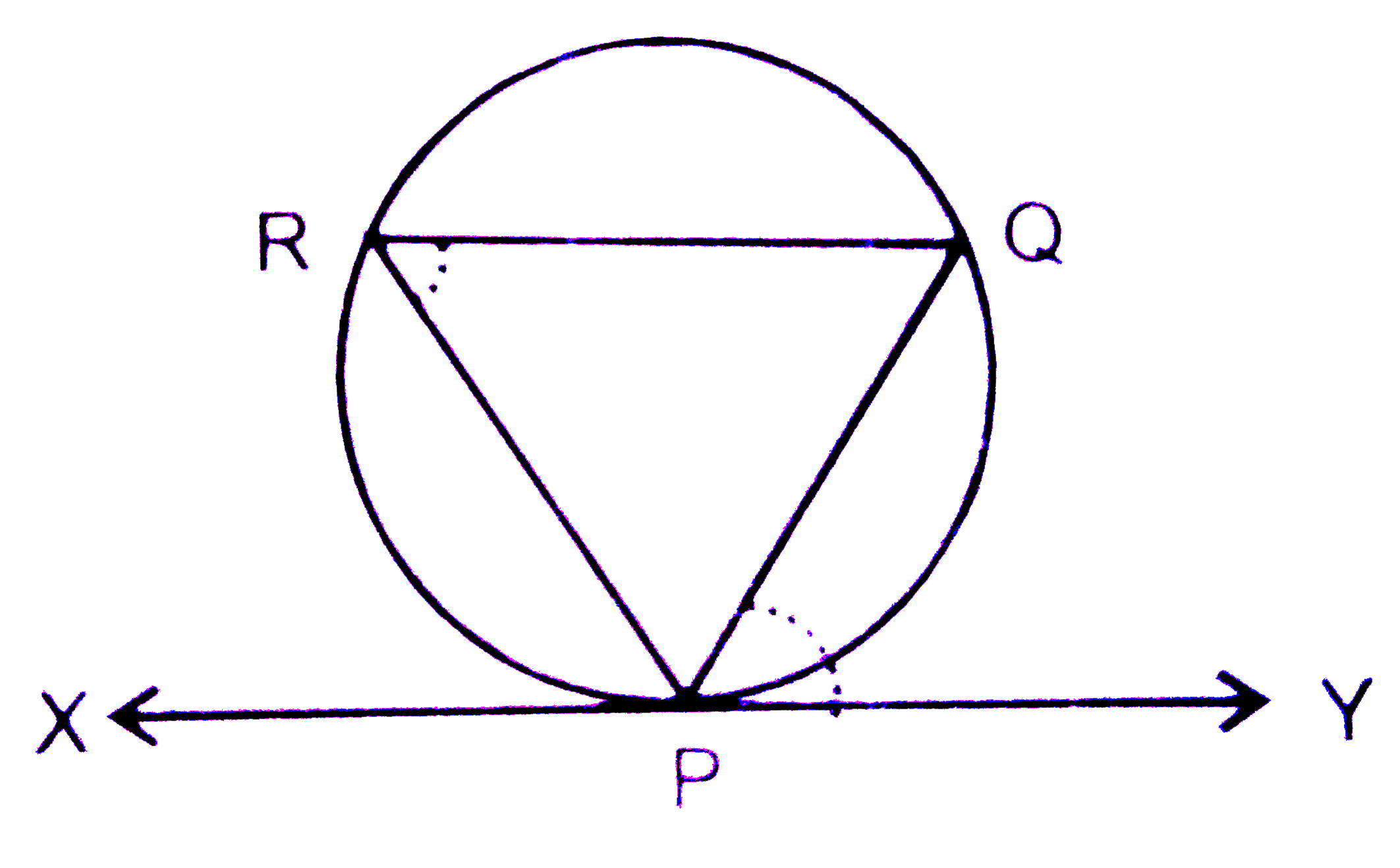
रचना के चरण:
चरण 1: 5cm त्रिज्या का एक वृत्त खींचें तथा इस पर एक बिन्दु P अंकित करें। बिन्दु P से वृत्त की एक जीवा PQ खींचें।
चरण 2: वृत्त पर एक (कोई) बिन्दु R अंकित करें और P एवं Q को R से मिला दें।
चरण 3: वृत्त के जीवा PQ के विपरीत में ∠QPY=∠PRQ बनाइए।
चरण 4: YP को X तक बढ़ाइए जिससे YPX अभीष्ट स्पर्श रेखा बन गई।
सारांश
इस अध्याय में, हमने देखा है कि निम्न रचनाएँ किस प्रकार की जाती हैं: