सांख्यिकी कक्षा 10 गणित
भूमिका
बच्चों! हमने कक्षा 9 में सांख्यिकी का परिचय देखा है, सांख्यिकी, गणित की वह शाखा है जिसमें आंकड़ों का संग्रहण, प्रदर्शन, वर्गीकरण और उसके गुणों का आकलन किया जाता है। हमने अवर्गीकृत आंकड़ों के लिए केन्द्रीय प्रवृत्ति के मापकों जैसे माध्य, माध्यक तथा बहुलक के बारे मे पढ़ा हैं। अब हम इन तीनों का अध्ययन वर्गीकृत आंकड़ों के लिए करेंगे। साथ ही हम संचयी बारंबारता (cumulative frequency) और संचयी बारंबारता सारणी की अवधरणाओं की चर्चा भी करेंगे तथा यह भी सीखेंगे कि संचयी बारंबारता वक्रों (cumulative frequency curves), जो तोरण (ogives) कहलाती हैं, को किस प्रकार खींचा जाता है।
आइए बच्चों सांख्यिकी को समझते है और करीब से...
बच्चों! कक्षा 9 मे हमने अवर्गीकृत आंकड़ों के लिए केन्द्रीय प्रवृत्ति के मापकों (माध्य, माध्यक, तथा बहुलक) को ज्ञात करना सीखा था।
यहाँ अवर्गीकृत आंकड़ों को समझने के लिए एक उदाहरण देखते है :
1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 8, 8, 8, 9
यहाँ सभी दिए आंकड़े भिन्न - भिन्न है अर्थात ये किसी समूह या वर्ग मे उपस्थित नहीं है, अवर्गीकृत आंकड़े कहलाते है। इन्हे आसानी से समझने के लिए बारंबारता सारणी के रूप मे व्यक्त किया जा सकता हैं।
| पद | बारंबारता |
|---|---|
| 1 | 4 |
| 2 | 3 |
| 3 | 3 |
| 4 | 2 |
| 5 | 2 |
| 6 | 3 |
| 7 | 2 |
| 8 | 3 |
| 9 | 1 |
यहाँ देख सकते है कि किसी एक पद का कितनी बार पुनरावृत्ति हुई है अर्थात बारंबारता कितना है। अब इन्हे हम वर्गों मे भी बाँट सकते है।
| वर्ग - अंतराल | पदों की संख्या |
|---|---|
| 1−4 | 10 |
| 4−8 | 9 |
| 8−12 | 4 |
यहाँ वर्ग अंतराल 1−4 मे पदों की सँख्या 10 है (1−4 मे 4 के पदों को सम्मिलित नहीं किया गया हैं) जिसमे 1 की बारंबारता 4, 2 की बारंबारता 3 तथा 3 की बारंबारता 3 है आगे वर्ग अंतराल 4−8 मे 4 की बारंबारता 2, 5 की बारंबारता 2, 6 की बारंबारता 3 तथा 7 की बारंबारता 2 है। इसी प्रकार आगे भी पदों की सँख्या लेकर सारणी बना सकते है, इस प्रकार के आंकड़े वर्गीकृत आंकड़े कहलाते है। इस अध्याय मे हम वर्गीकृत आंकड़ों से संबंधित गणनाओ का अध्ययन करेंगे।
वर्गीकृत आंकड़ों का माध्य
हम जानते है कि यदि हमे अवर्गीकृत आंकड़े (प्रेक्षण) दिए गए हो तो उनके माध्य का मान, प्रेक्षणों का योग करके उन्हे प्रेक्षणों की कुल सँख्या से भाग देने पर प्राप्त होता है।
यदि निम्न प्रेक्षण दिए गए हैं,
x1,x2,x3.........xn
जहाँ प्रेक्षणों की संख्या n हैं तब
प्रेक्षणों का माध्य =x1+x2+x3+.........+xnn
अब यदि इसी प्रकार दिए गए प्रेक्षण वर्गीकृत रूप में दिए गए हो अर्थात प्रेक्षण x1, x2, x3....xn की बारंबारता क्रमशः f1, f2, f3....fn दिए गए हो तो
यहाँ प्रेक्षणों की सँख्या कितनी होगी?
आइए इसे समझते है जैसा की ऊपर हम देख सकते है x1 की बारंबारता f1 है अर्थात x1, f1 बार आया है। अतः x1 को f1 बार गिना जा सकता है। उसी प्रकार x2 को f2 बार गिना जाएगा यही सभी प्रेक्षणों के लिए कहा जा सकता है। अतः सभी प्रेक्षणों के बारंबारता का योग करने से प्रेक्षणों की सँख्या प्राप्त होगी।
प्रेक्षणों की सँख्या =∑fi
=f1+f2+f3+.....+fn
अब यहाँ प्रेक्षणों का योग ज्ञात करते है, जैसे की अवर्गीकृत प्रेक्षणों मे सभी प्रेक्षणों को जोड़ने पर प्रेक्षणों का योग प्राप्त होता है। परन्तु वर्गीकृत प्रेक्षणों मे प्रत्येक प्रेक्षण की बारंबारता दिया गया है। सभी प्रेक्षणों का योग करने के लिए प्रत्येक प्रेक्षण के लिए जितनी बारंबारता है, उतने बार योग करके सभी को जोड़ना होगा।
प्रेक्षणों का योग =∑xi⋅fi
=x1⋅f1+x2⋅f2+x3⋅f3+......+xn⋅fn
अतः माध्य ¯x=∑xi⋅fi∑fi
¯x=x1⋅f1+x2⋅f2+......+xn⋅fnf1+f2+.....+fn
अब यदि हमे वर्ग - अंतराल ज्ञात हो तब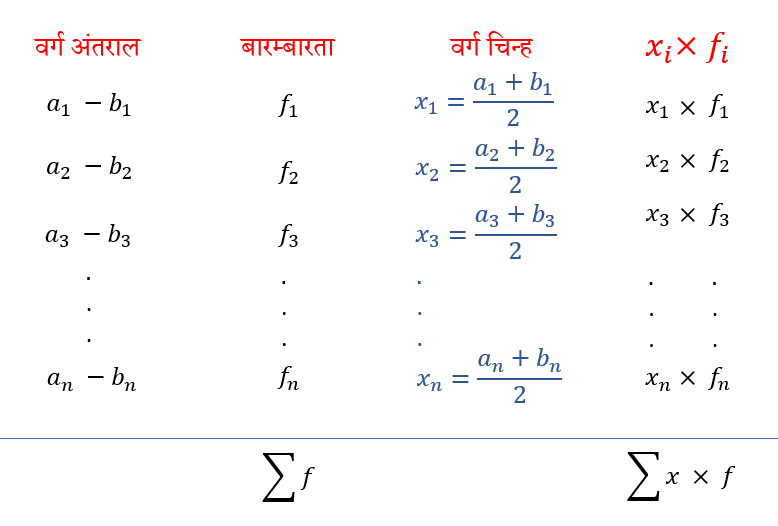
यहाँ वर्ग अंतरालों के मध्य एक ऐसे बिन्दु (मध्य बिन्दु) को लेते है जिसका मान उस अंतराल मे उपस्थित सभी मानो का केंद्र माना जाता है, यहाँ मान लिया जाता है की उस वर्ग अंतराल की बारंबारता उस बिन्दु के चारों ओर केंद्रित है, वर्ग चिह्न कहलाता है।
वर्ग चिह्न (xi)=
जैसा की ऊपर चित्र मे दर्शाया गया है।
यहाँ
माध्य ¯x=∑xifi∑fi
उपरोक्त विधि प्रत्यक्ष विधि (direct method) कहलाता है।
कल्पित माध्य विधि (Assumed Mean Method)
बच्चों सर्वप्रथम अवर्गीकृत आंकड़ों के लिए समझने का प्रयास करते है,
यदि हमारे पास कुछ आंकड़े निम्न प्रकार से दिए गए हो :
5,10,15,20,25,30
अतः, माध्य =5+10+15+20+25+306=17.5
अब इन आंकड़ों के मध्य किसी अंक को इनका कल्पित माध्य मान सकते है, यहाँ आंकड़ों की सँख्या सम है तो 15 या 20 मे से किसी एक को कल्पित माध्य लेंगे। माना, 15 कल्पित माध्य है तब यहाँ प्रत्येक आंकड़ों का विचलन ज्ञात किया जा सकता है। विचलन से तात्पर्य है की कोई सँख्या अपने कल्पित माध्य से कितने अंतर पर है।

यहाँ देख सकते है जिस मान को कल्पित माध्य मानकर सभी आंकड़ों से घटाया गया था अंत मे माध्य विचलन मे जोड़ दिया गया, जिससे उचित माध्य (17.5) प्राप्त हुआ। यह विधि वर्गीकृत आंकड़ों के लिए अधिक उपयोगी है।
आइए वर्गीकृत आंकड़ों के लिए इस विधि को निम्न बिन्दुओ से समझते है:
अतः di=xi−a
यहाँ विचलन का प्रयोग संख्याओ का मान कम करके गणना आसान बनाने के लिए किया जाता है, जिससे हल आसान हो जाए।
माध्य विचलन ¯d=∑fi∑fi
¯x=a+¯d
आइए इसे एक उदाहरण से समझने का प्रयास करते है:
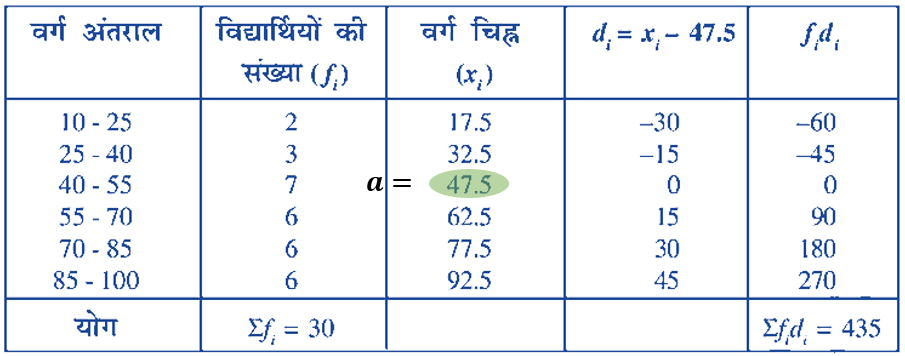
प्रश्न मे एक कक्षा के बच्चों का प्राप्तांक वर्ग अंतरालों मे दिया गया है तथा प्रत्येक वर्ग अंतराल के अंतर्गत आने वाले प्राप्तांक को प्राप्त करने वाले बच्चों की सँख्या दी गई है। यहाँ हम देख सकते है की वर्ग अंतरालों के (औसत अंक) वर्ग चिह्न (xi) निकाले गए है, चूंकि वर्ग चिन्हों की सँख्या 6 (सम) है अतः इसके मध्य मे 2 वर्ग चिह्न 47.5 व 62.5 आते है इनमे से किसी एक मान (a=47.5) को कल्पित माध्य मानकर उसे प्रत्येक वर्ग चिह्न से घटाकर विचलन (di) ज्ञात किया गया।
अब यदि यहाँ सभी बच्चों के लिए प्राप्तांक का माध्य ज्ञात करना है तो हम जानते है कि
माध्य ¯x=a+¯d
माध्य ¯x=a+∑fidi∑fi
यहाँ
कल्पित माध्य a=47.5 (माना)
माध्य विचलन ¯d=∑fidi∑fi=43530=14.5
अतः माध्य ¯x=a+∑fidi∑fi
=47.5+14.5=62
पग - विचलन विधि (Step Deviation Method)
बच्चों! जैसे की हमने पहले माध्य ज्ञात करने की प्रत्यक्ष विधि व कल्पित माध्य विधि देखा। कल्पित माध्य विधि मे, प्रत्यक्ष विधि से गणना सरल बनाने के लिए कल्पित माध्य को प्रत्येक वर्ग चिह्न से घटाया जाता है तथा माध्य विचलन ज्ञात कर उसे कल्पित माध्य से जोड़ा जाता है।
पग विचलन विधि मे एक और पद वर्ग माप का उपयोग किया जाता है। वर्ग माप, वर्ग अंतरालों के मध्य का अंतर होता है।
यहाँ कल्पित माध्य विधि से एक कदम आगे बढ़कर विचलनों को वर्ग माप से भाग दिया जाता है, जिससे प्राप्त मान और छोटा प्राप्त हो जिससे गणना करने मे आसानी हो।
आइए पग विचलन विधि को निम्न बिन्दुओ से समझते है:
यहाँ di=xi−a
यहाँ विचलन का प्रयोग संख्याओ का मान कम करके गणना आसान बनाने के लिए किया जाता है, तथा साथ ही वर्ग माप से भाग देने पर गणना और अधिक आसान हो जाती है।
¯u=∑fiui∑fi
तथा वर्ग माप h से ¯u का गुणा करेंगे।
चूँकि ui ज्ञात करने के लिए प्रत्येक पद का h से भाग दिया गया था,
अतः माध्य ज्ञात करने के लिए ui के माध्य से h का गुणा करेंगे।
अतः
¯x=a+h⋅¯u
आइए इसे पूर्व मे लिए गए उदाहरण से समझने का प्रयास करते है:
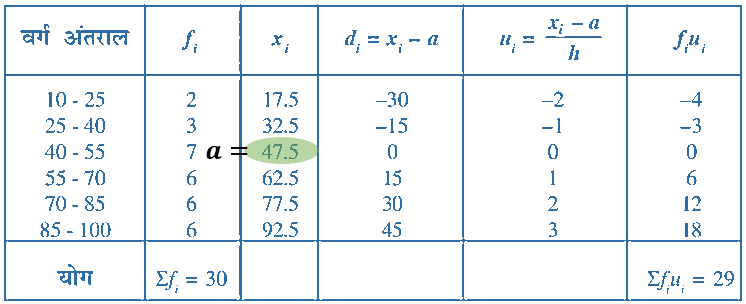
जैसे की हमने पूर्व मे a=47.5 को कल्पित माध्य मानकर उसे प्रत्येक वर्ग चिह्न से घटाकर विचलन (di) ज्ञात किया था।
अब प्रत्येक विचलन को वर्गमाप h=15 से भाग देंगे जिससे प्रत्येक के लिए ui प्राप्त होगा।
यदि यहाँ सभी बच्चों के लिए प्राप्तांक का माध्य ज्ञात करना है तो हम जानते है की
¯x=a+h⋅¯u
यहाँ
कल्पित माध्य a=47.5 (माना)
वर्ग माप h=15
¯u=∑fiui∑fi
अतः माध्य ¯x=a+h⋅¯u
¯x=a+h⋅∑fiui∑fi
¯x=47.5+15×2930=62
OMR (One Minute Revision)
वर्गीकृत आंकड़ों का माध्य निम्नलिखित तीन विधियों से ज्ञात किया जा सकता है:
प्रत्यक्ष विधि : ¯x=∑fixi∑fi
कल्पित माध्य विधि : ¯x=a+∑fidi∑fi
पग - विचलन विधि : ¯x=a+(∑fiui∑fi)×h
उदाहरण 1
छात्रों के एक समूह द्वारा अपने पर्यावरण संचेतना अभियान के अंतर्गत एक सर्वेक्षण किया गया जिसमें उन्होनें एक मोहल्ले के 20 घरों में लगे हुए पौधों से संबंधित निम्नलिखित आंकड़े एकत्रित किए। प्रति घर माध्य पौधे की संख्या ज्ञात कीजिए।

प्रत्येक वर्ग अंतराल के लिए वर्ग - चिह्न (xi) ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग करेंगे:
वर्ग चिह्न (xi)=
xi तथा fixi की गणना निम्नलिखित है:
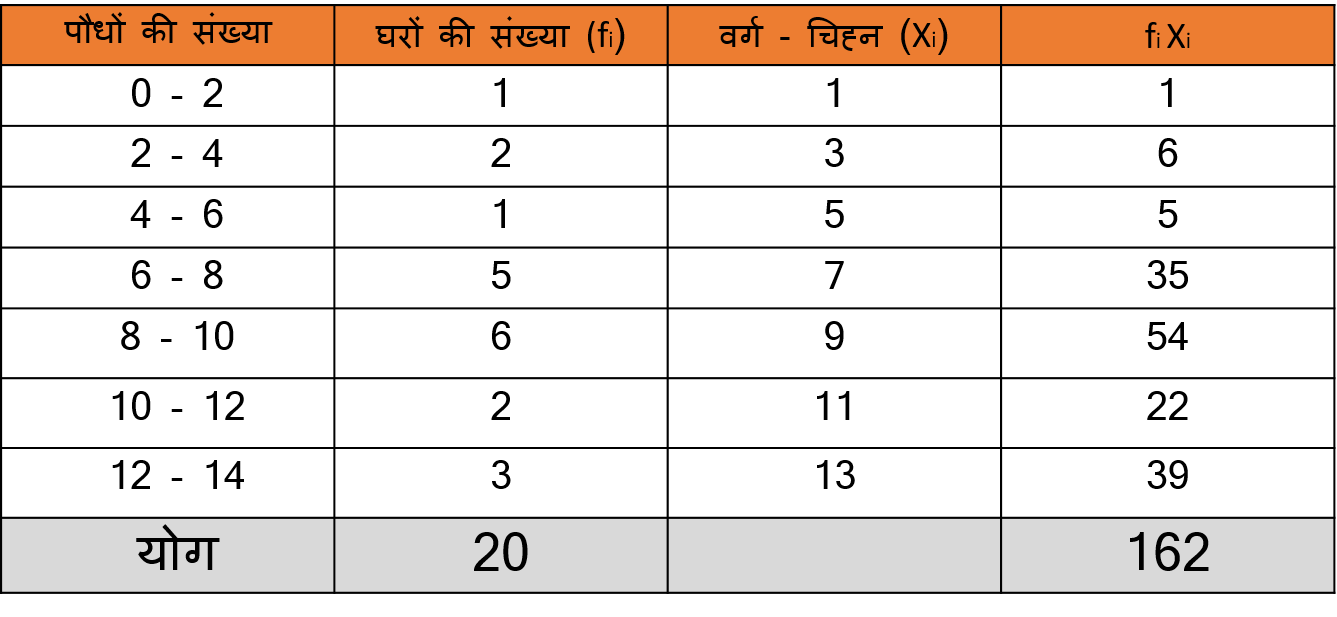
यहाँ, सारणी से हमें निम्नलिखित मान प्राप्त होते हैं:
Σfixi=162 तथा Σfi=20
हम जानते हैं कि
माध्य ¯x=ΣfixiΣf=16220=8.1
अतः प्रति घर माध्य पौधों की संख्या 8.1 है।
Note यहाँ, माध्य ज्ञात करने के लिए प्रत्यक्ष विधि का प्रयोग किया है क्योंकि (xi) और (fi) के मान छोटे है।
उदाहरण 2
निम्नलिखित बारंबारता बंटन के लिए कल्पित माध्य विधि (लघु विधि ) से माध्य ज्ञात कीजिए।

यहाँ मध्य के वर्ग अंतराल 30−40 है, इसका औसत 30+402=35 होगा।
अतः कल्पित माध्य a=35
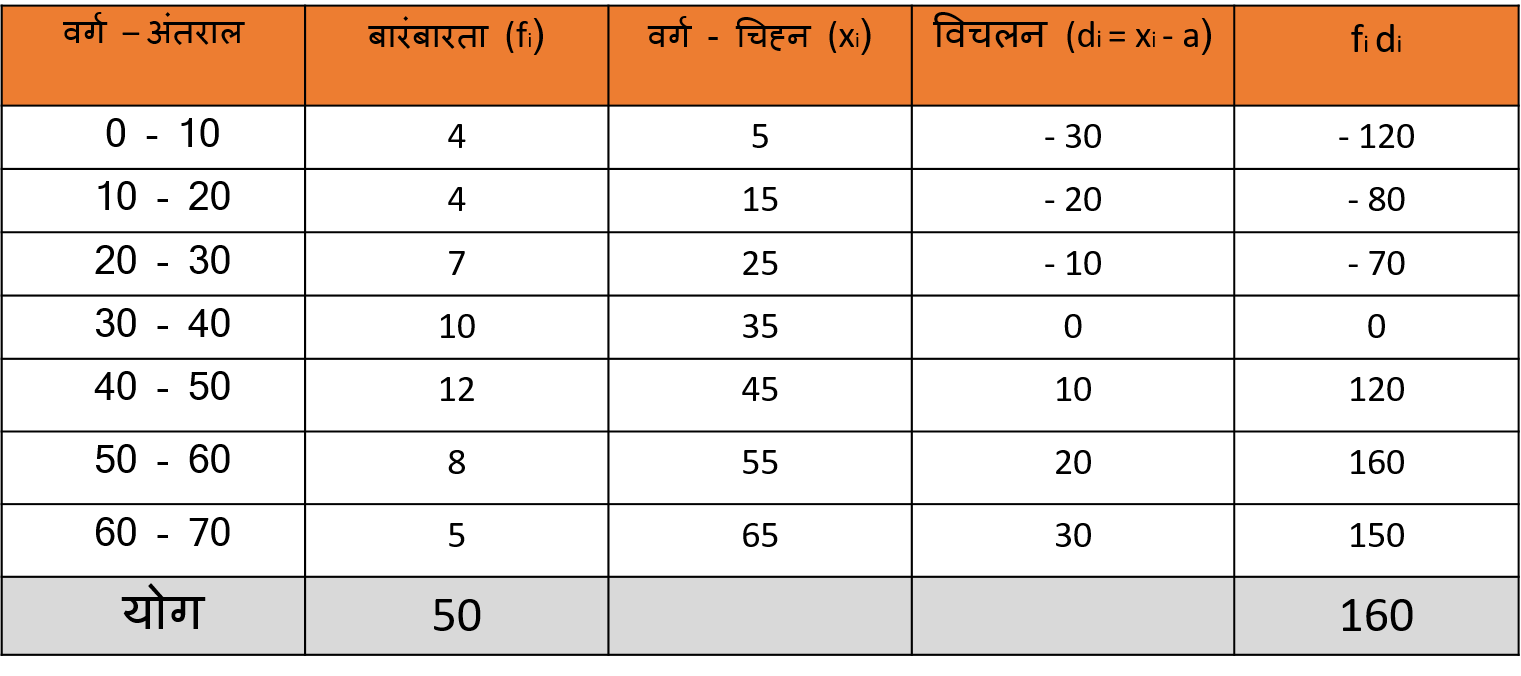
यहाँ, सारणी से हमे निम्नलिखित मान प्राप्त होते हैं:
Σfi=50 और Σfi=160
हम जानते हैं कि,
माध्य ¯x=a+ΣfiΣfi
=35+16050
=35+3.2=38.2
अतः दिए गए बारंबारता बंटन का माध्य 38.2 हैं
उदाहरण 3
नीचे दी हुई सारणी भारत के विभिन्न राज्यों एवं संघीय क्षेत्रों के ग्रामीण क्षेत्रों के प्राथमिक विद्यालयों में महिला शिक्षकों के प्रतिशत बंटन को दर्शाती है। इन अनुच्छेद में चर्चित तीनों विधियों से महिला शिक्षकों का माध्य प्रतिशत ज्ञात कीजिए।

यहाँ प्रत्येक वर्ग अंतराल के लिए वर्ग चिह्न (xi) ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग करेंगे:
वर्ग चिह्न (x)=
मध्य के वर्ग अंतराल 45−55 है, इसका औसत 45+552=50 होगा।
अतः कल्पित माध्य a=50
वर्गमाप h=10, विचलन di=xi−50 तथा ui=xi−5010
निम्नलिखित सारणी से ∑fi, ∑fixi, ∑fi तथा ∑fiui ज्ञात करते हैं :
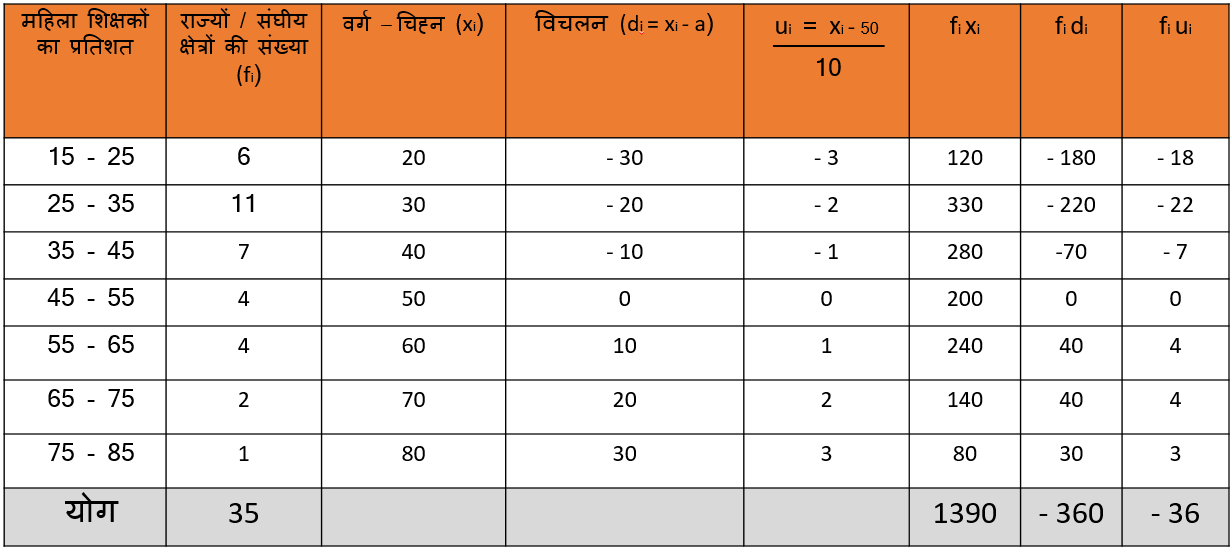
स्पष्ट हैं की,
∑fi=35
∑fixi=1390
∑fi=−360
∑fiui=−36
हम जानते हैं कि, माध्य
प्रत्यक्ष विधि से, ¯x=∑fixi∑fi=139035=39.71
कल्पित माध्य विधि से, ¯x=a+∑fi∑fi=50+−36035=39.71
पग - विचलन विधि से, ¯x=a+(∑fiui∑fi)×h=50+−3635×10=39.71
अतः, ग्रामीण क्षेत्रों के प्राथमिक विद्यालयों में महिला शिक्षकों का माध्य प्रतिशत 39.71 है।
उदाहरण 4
यदि निम्नलिखित आकड़ों का माध्य 26 है, तो P का मान ज्ञात कीजिए
| वर्ग - अंतराल | 0−10 | 10−20 | 20−30 | 30−40 | 40−50 |
| बारंबारता | 6 | p | 9 | 4 | 11 |
दिया हैं;
माध्य = 26
अज्ञात बारंबारता P=?
प्रत्येक वर्ग अंतराल के लिए वर्ग - चिह्न (xi) ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग करेंगे:
वर्ग चिह्न (xi)=
xi तथा fixi की गणना निम्नलिखित है:
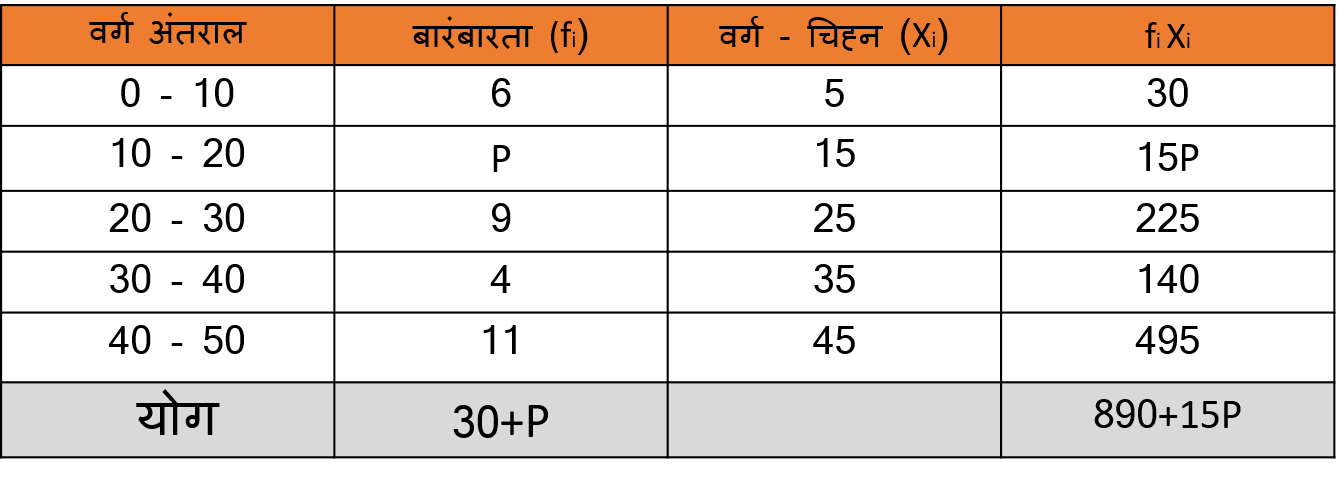
यहाँ, सारणी से हमें निम्नलिखित मान प्राप्त होते हैं:
Σfixi=890+15P तथा Σfi=30+P
हम जानते हैं कि (प्रत्यक्ष विधि से),
माध्य ¯x=ΣfixiΣf
⇒26=890+15p30+p
⇒780+26p=890+15p
⇒11p=110
⇒p=10
वर्गीकृत आंकड़ों का बहुलक
हम जानते हैं कि, किसी बंटन का बहुलक चर का वह मान होता है जो सबसे अधिक बार आता है, इस प्रकार बहुलक वह प्रेक्षण है जिसकी बारंबारता सबसे अधिक होती है। पिछली कक्षाओं मे हमने अवर्गीकृत आंकड़ों के लिए बहुलक निकालना सीखा था।
आइए एक उदाहरण से इसका पुनरावलोकन करते है।
कोई खिलाड़ी यदि 10 मैच खेलता है तथा 10 मैचों मे निम्न विकेट लेता है
1,2,4,2,3,2,5,0,4,2
यहाँ उस विकेट की सँख्या की बारंबारता निकालते है, जो उसने सबसे अधिक बार ली है तो वह होगा 2 विकेट जो की सबसे अधिक चार बार आया है। अतः यहाँ बहुलक 2 होगा।
वर्गीकृत बारंबारता बंटन की स्थिति में सिर्फ बारंबारताओं को देखकर बहुलक के मान को जानना संभव नहीं है। वर्गीकृत बारंबारता बंटन का बहुलक ज्ञात करने के लिए सर्वप्रथम हम उस वर्ग को ज्ञात करते हैं जिसमें बहुलक रहता है। जिस वर्ग में बहुलक रहता है उसे बहुलक वर्ग कहते हैं। स्पष्ट है कि बहुलक वर्ग की बारंबारता सबसे अधिक होंगी। यदि l बहुलक वर्ग की निम्न सीमा है और h वर्ग अंतराल तब बहुलक का मान l और l+h के बीच कहीं होगा।
बहुलक वर्ग को निर्धारित करने के बाद बहुलक ज्ञात करने के लिए हम निम्नलिखित सूत्र का प्रयोग करते हैं।
बहुलक =l+f1−f02f1−f0−f2×h
जहाँ
l= बहुलक वर्ग की निम्न सीमा
h= वर्ग अंतराल की माप
f1= बहुलक वर्ग की बारंबारता
f0= बहुलक वर्ग से ठीक पहले के वर्ग की बारंबारता
f1= बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता
Note:- यहाँ सभी अंतरालों का वर्ग माप बराबर होना आवश्यक है।
आइए नीचे दिए गए आंकड़ों के लिए बहुलक ज्ञात करते है:
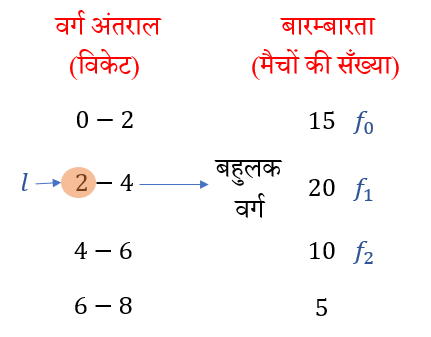
बहुलक वर्ग - जिस वर्ग की बारंबारता अधिकतम हो।
ऊपर दिए गए आंकड़ों मे हम देख सकते है की बहुलक वर्ग 2 - 4 है।
बहुलक वर्ग ज्ञात होने के पश्चात हम अन्य मान जैसे की l, f1, f0, f2 आसानी से ज्ञात कर सकते है।
चूँकि बहुलक वर्ग की निम्न सीमा 2 है अतः l=2
बहुलक वर्ग की बारंबारता f1=20
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता f0=15
बहुलक वर्ग के ठीक बाद वाले वर्ग की बारंबारता f2=10
तथा प्रत्येक वर्ग अंतराल की वर्ग माप h=2
अतः, बहुलक =l+f1−f02f1−f0−f2×h
=2+20−152×20−15−10×2
=2+540−25×2
=2+515×2
=2+23
=83
=2.667
अतः उपरोक्त आंकड़ों का बहुलक 2.667 है।
OMR (One Minute Revision)
बहुलक =l+f1−f02f1−f0−f2×h
जहाँ
l= बहुलक वर्ग की निम्न सीमा
h= वर्ग अंतराल की माप
f1= बहुलक वर्ग की बारंबारता
f0= बहुलक वर्ग से ठीक पहले के वर्ग की बारंबारता
f1= बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता
उदाहरण 5
निम्नलिखित आंकड़े 225 बिजली उपकरणों के प्रेक्षित जीवनकाल (घंटो में) की सूचना देते है :

उपकरणों का बहुलक जीवनकाल ज्ञात कीजिये।
दिए गए बारंबारता बंटन में वर्ग 60 - 80 की बारंबारता महत्तम (61) है और इसलिए यह बहुलक वर्ग है।
अब, बहुलक =l+(f1−f02f1−f0−f2)×h
यहाँ,
l= बहुलक वर्ग की निम्न सीमा =60
f1= बहुलक वर्ग की बारंबारता =61
f0 = बहुलक वर्ग के ठीक पहले वाले वर्ग की बारंबारता =52
f2= बहुलक वर्ग के ठीक बाद के वर्ग की बारंबारता = 38
h= वर्ग अंतराल की माप =20
∴ बहुलक =60+61−522×61−52−38×20
=60+932×20
=60+458
=65.625
अतः उपरोक्त आंकड़ों का बहुलक 65.625 है।
उदाहरण 6
निम्नलिखित आंकड़े में लुप्त बारंबारता ज्ञात कीजिये यदि बहुलक 25 है।

चूंकि बहुलक 25 है और यह वर्ग 20 - 30 में है अतः बहुलक वर्ग 20 - 30 है। माना की लुप्त बारंबारता x है।
हम जानते हैं कि,
बहुलक =l+f1−f02f1−f0−f2×h
यहाँ,
l= बहुलक वर्ग की निम्न सीमा =20
f1= बहुलक वर्ग की बारंबारता =27
f0= बहुलक वर्ग के ठीक पहले वाले वर्ग की बारंबारता =22
f2= बहुलक वर्ग के ठीक बाद के वर्ग की बारंबारता =x
h= वर्ग अंतराल की माप =10
⇒25=20+27−2254−22−x×10
⇒25=20+532−x×10
⇒5=5032−x
⇒32−x=10
⇒x=22
अतः अज्ञात बारंबारता 22 हैं।
वर्गीकृत आंकड़ों का माध्यक
बच्चों! जैसा की हमने माध्यक के बारे मे पहले पढ़ा हुआ है, आइए इसका पुनरावलोकन कर लेते है।
माध्यक (median) : केंद्रीय प्रवृत्ति का ऐसा मापक है, जो आंकड़ों में सबसे बीच के अर्थात मध्य के प्रेक्षण का मान देता है। प्रेक्षणों को आरोही या अवरोही क्रम में रखने पर प्रेक्षणों का एक ऐसा मान जो सभी प्रेक्षणों को अपने दोनों तरफ बराबर - बराबर संख्या में विभाजित करे, माध्यक कहलाता है।
माध्यक निकालने के लिए दो स्थितियाँ हैं:-
(i) जब प्रेक्षणों की संख्या (n) विषम हो:
माध्यक =n+12 वें प्रेक्षण का मान
(ii) जब प्रेक्षणों की संख्या (n) सम हो:
माध्यक =n2 वें और (n2+1) वें प्रेक्षणों के मानों का माध्य होता है।
अतः, माध्यक =12{(n2) वें प्रेक्षण का मान +(n2+1) वें प्रेक्षण का मान}
अब यदि आंकड़ों की सँख्या बहुत अधिक हो तथा आंकड़ों की बारंबारता दी गई हो तो माध्यक ज्ञात करने के लिए संचयी बारंबारता (Cumulative frequency) निकाला जाता है। संचयी बारंबारता सारणी दो प्रकार के होते हैं:
(i) कम प्रकार का (ii) अधिक प्रकार का
जैसा की हम जानते है किसी सारणी में प्रेक्षणों के लिए बारंबारता होता है, जो दर्शाता है की उस प्रेक्षण की कितने बार पुनरावृत्ति हुई है। उसी प्रकार संचयी बारंबारता की गणना बारंबारता के योग से करते हैं। संचयी बारंबारता की गणना करने के लिए दिये गये बारंबारता वितरण तालिका से प्रथम बारंबारता से योग शुरू कर अन्तिम बारंबारता का योग करते हैं। इसका अन्तिम योग का मान कुल बारंबारता के योग के बराबर आता है। क्योंकि सभी बारंबारता को अन्त में योग किया जाता है।
आइए एक उदाहरण देखते है: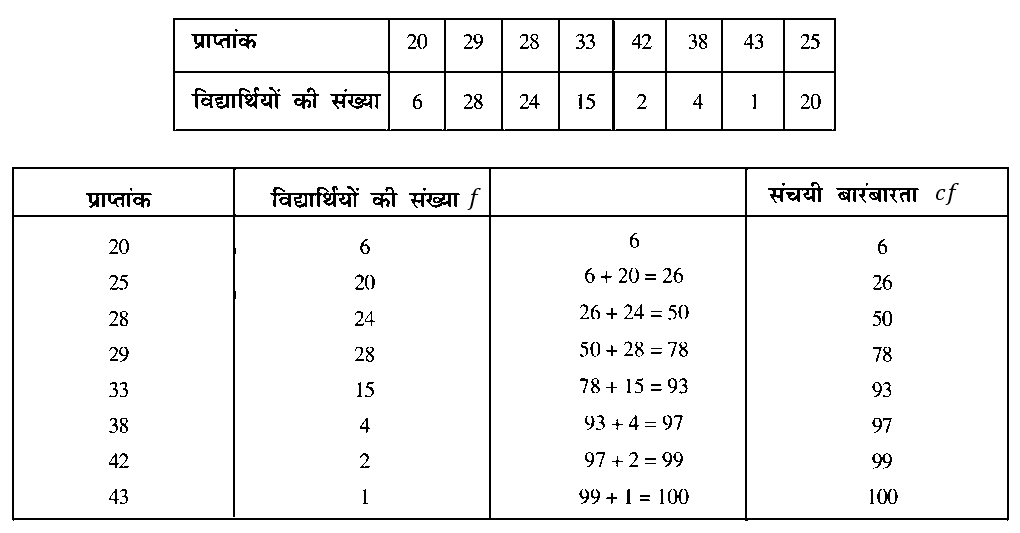
ऊपर उदाहरण देखने से पता चलता है की दिए गए प्राप्तांक के सामने उसे प्राप्त करने वाले छात्रों की सँख्या दी गई है, अर्थात प्राप्तांक की बारंबारता दी गई है। अब यदि संचयी बारंबारता निकालते है तो प्रथम प्रेक्षण 20 के लिए बारंबारता 6 व संचयी बारंबारता 6 समान होती है। आगे दूसरे प्रेक्षण 25 के लिए बारंबारता 20 व संचयी बारंबारता 6+20=26 प्राप्त होता है। यहाँ संचयी बारंबारता 26 से तात्पर्य है की उसके सामने का प्राप्तांक अर्थात 25 अंक तक अर्थात 25 से कम या बराबर अंक प्राप्त करने वाले छात्रों की सँख्या 26 है इसी प्रकार आगे भी समझ सकते है। इस प्रकार की सारणी कम प्रकार का संचयी बारंबारता बंटन कहलाता है।
यहाँ छात्रों की कुल सँख्या 100 है, अतः n=100 जो की एक सम सँख्या है।
माध्यक =12{(n2)वाँ पद +(n2+1) वाँ पद}
=12{(1002)वाँ पद +(1002+1) वाँ पद}
=12(50 वाँ पद +51 वाँ पद)
=28+292
=28.5
(चूंकि 50 वे पद मे देखे प्राप्तांक 28 तथा 51 वे पद मे प्राप्तांक 29 है)
अतः यहाँ छात्रों के प्राप्तांकों का माध्यक 28.5 है।
कम प्रकार के संचयी बारंबारता सारणी के विपरीत यदि कुल बारंबारता से नीचे आते हुए बारंबारताओं से घटाया जाता हैं तब सारणी अधिक प्रकार का संचयी बारंबारता बंटन कहलाता है।
उदाहरण के लिए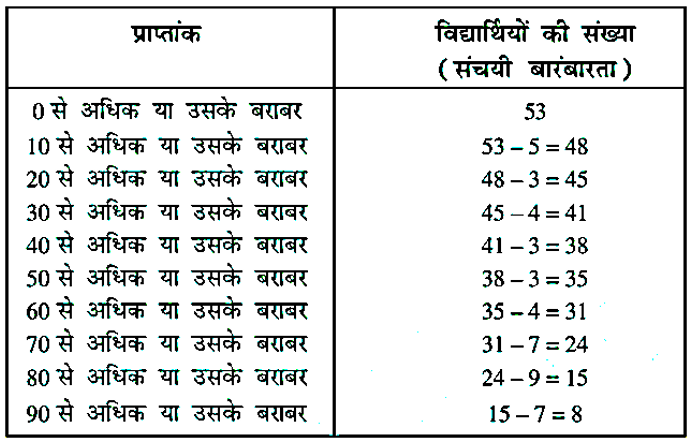
वर्गीकृत आंकड़ों का माध्यक ज्ञात करना : अब यदि आंकड़े वर्ग अंतरालों के रूप मे दिए गए हो तो उसे हल करने के लिए निम्न सूत्र का प्रयोग किया जाता है
माध्यक =l+(n2−cff)×h
यहाँ,
l= माध्यक वर्ग की निम्न सीमा
n= प्रेक्षणों की संख्या
cf= माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f= माध्यक वर्ग की बारंबारता
h= वर्ग माप
इसके लिए आइए एक उदाहरण लेते है -
यदि कुल प्राप्तांक 100 हो तथा कक्षा मे छात्रों की सँख्या 53 हो तब देखते है निम्न दिए गए आंकड़ों की सहायता से किस प्रकार माध्यक ज्ञात किया जा सकता है:
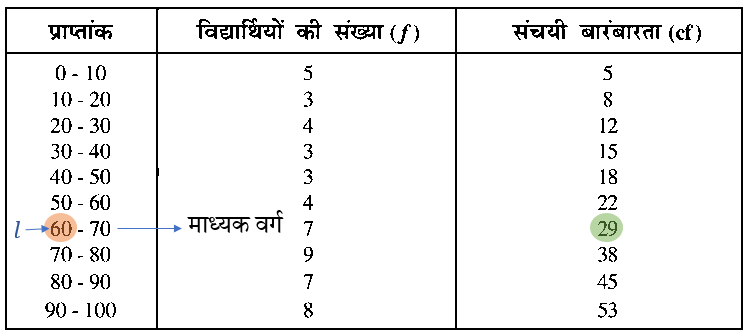
सर्वप्रथम माध्यक वर्ग (median class) ज्ञात करते हैं, आइए जानते है इसे कैसे ज्ञात किया जा सकता है। इसके लिए सभी वर्गों का संचयी बारंबारता तथा n2 का मान ज्ञात करना है। अंतराल जो उस संचयी बारंबारता के सामने हो, जिसका मान n2 से अधिक तथा निकटतम हो, माध्यक वर्ग कहलाता है।
जहाँ n कुल बारंबारता का मान है।
यहाँ n=53 है, अतः n2=532=26.5 है।
ऊपर सारणी मे देखे, संचयी बारंबारता का वह मान जो 26.5 से अधिक तथा निकटतम हो 29 प्राप्त होगा। अतः माध्यक वर्ग 60−70 है।
यहाँ निम्न सीमा l=60 तथा वर्ग माप h=10 है।
माध्यक वर्ग से ठीक पहले वर्ग की संचयी बारंबारता cf=22 तथा माध्यक वर्ग की बारंबारता f=7
इस प्रकार
माध्यक =l+(n2−cff)×h
=60+532−227×10
=60+927×10
=60+92×17×10
=60+457
=66.4
माध्यक 66.4 से तात्पर्य है की आधे छात्रों को 66.4 से कम अंक प्राप्त हुआ तथा आधे छात्रों ने 66.4 से अधिक या उसके बराबर अंक प्राप्त किये।
Note : केन्द्रीय प्रवृत्ति के मापको मे निम्नलिखित संबंध प्राप्त होता है:
3 माध्यक = बहुलक +2 माध्य
OMR (One Minute Revision)
माध्यक =l+(n2−cff)×h
यहाँ
l= माध्यक वर्ग की निम्न सीमा
n= प्रेक्षणों की संख्या
cf= माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f= माध्यक वर्ग की बारंबारता
h= माध्यक वर्ग का माप
उदाहरण 7
कक्षा X के 30 विद्यार्थियों के भारों का वितरण निम्न सारणी में दर्शाया गया है। विद्यार्थी का माध्यक भार ज्ञात करें।

माध्यक ज्ञात करने के लिए, संचयी बारंबारताओं के साथ बारंबारता बंटन सरणी निम्नलिखित है:
| भार (Kg में) | विद्यार्थियों की संख्या (fi) | संचयी बारंबारता (cf) |
|---|---|---|
| 40−45 | 2 | 2 |
| 45−50 | 3 | 2+3=5 |
| 50−55 | 8 | 5+8=13 |
| 55−60 | 6 | 6+13=19 |
| 60−65 | 6 | 6+19=25 | 65−70 | 3 | 3+25=28 |
| 70−75 | 2 | 2+28=30 |
| योग | 30 |
बारंबारता सरणी से, n=30
इसलिए, n2=302=15 है। यह प्रेक्षण अंतराल 55 - 60 में आता है।
अतः माध्यक वर्ग = 55 - 60
माध्यक वर्ग की निम्न सीमा (l)=55
वर्ग माप (h)=5
माध्यक वर्ग की बारंबारता (f)=6
माध्यक वर्ग से ठीक पहले वर्ग की संचयी बारंबारता (cf)=13
हम जानते हैं कि,
माध्यक =l+n2−cff×h
=55+15−136×5
=55+1067
=55+1.67
=56.67
अतः, विद्यार्थियों का माध्यक भार 56.67kg है।
उदाहरण 8
निम्नलिखित आंकड़े का माध्यक 52.5 है। x और y के मान ज्ञात करे यदि कुल बारंबारता 100 है।
| वर्ग - अंतराल | बारंबारता |
|---|---|
| 0−10 | 2 | 10−20 | 5 | 20−30 | x |
| 30−40 | 12 |
| 40−50 | 17 |
| 50−60 | 20 |
| 60−70 | y |
| 70−80 | 4 |
| 80−90 | 7 |
| 90−100 | 4 |
उपरोक्त बंटन का एक कम प्रकार का संचयी बारंबारता बंटन निम्नलिखित है::
| वर्ग - अंतराल | बारंबारता (fi) | संचयी बारंबारता (cf) |
|---|---|---|
| 0−10 | 2 | 2 | 10−20 | 5 | 7 | 20−30 | x | 7+x |
| 30−40 | 12 | 19+x |
| 40−50 | 17 | 36+x |
| 50−60 | 20 | 56+x |
| 60−70 | y | 56+x+y |
| 70−80 | 9 | 65+x+y |
| 80−90 | 7 | 72+x+y |
| 90−100 | 4 | 76+x+y |
| 100 |
सारणी से, 76+x+y=100
⇒x+y=100−76=24
∴y=24−x …(i)
माध्यक =52.5 (दिया हुआ है)
यहाँ, n=100
इसलिए, n2=1002=50 है। यह प्रेक्षण वर्ग अंतराल 50 - 60 में आता है।
अतः माध्यक वर्ग = 50 - 60
माध्यक वर्ग की निम्न सीमा (l)=50
वर्ग माप (h)=10
माध्यक वर्ग की बारंबारता (f)=20
माध्यक वर्ग से ठीक पहले वर्ग की संचयी बारंबारता (cf)=36+x
हम जनते हैं कि,
माध्यक =l+n2−cff×h
∴52.5=50+50−(36+x)20×10
⇒52.5−50=50−36−x2
⇒2.51=14−x2
⇒5=14−x
⇒x=14−5=9
x का मान (i) में रखने पर
y=24−9=15
∴x=9, y=15
संचयी बारंबारता बंटन का आलेखीय निरूपण
संचयी बारंबारता वक्र या तोरण : जब वर्ग अन्तरालों की संचयी बारंबारताओं को वर्ग-अंतराल की उच्च सीमा या निम्न सीमा के विरुद्ध ग्राफ पेपर पर अंकित (plot) किया जाता है, जिसमें वर्ग-अन्तरालों की उच्च या निम्न सीमा को X- अक्ष (क्षैतिज अक्ष) पर तथा संचयी बारंबारता को Y- अक्ष (ऊर्ध्वाधर अक्ष) पर लेकर, बिन्दुओं को अंकित कर इन्हें मुक्त हस्त (free hand) से मिलाने से हमें जो वक्र प्राप्त होती है वह एक संचयी-बारंबारता वक्र या तोरण कहलाती है
तोरण दो प्रकार के होते हैं : (i) कम प्रकार का तोरण (ii) अधिक प्रकार का तोरण
कम प्रकार का तोरण : वर्ग-अन्तरालों की ऊपरी सीमा को X- अक्ष (क्षैतिज अक्ष) पर और संगत संचयी बारंबारता (कम प्रकार का) को Y- अक्ष (ऊर्ध्वाधर अक्ष) पर लेकर बिन्दुओं को अंकित कर इन्हें मुक्त-हस्त से मिलाने पर प्राप्त तोरण, 'कम प्रकार का' तोरण कहलाता है
अधिक प्रकार का तोरण : वर्ग- अन्तरालों की निम्न सीमा को X- अक्ष (क्षैतिज अक्ष) पर और संगत संचयी बारंबारता (अधिक प्रकार का) को Y- अक्ष (ऊर्ध्वाधर अक्ष) पर लेकर बिन्दुओं को अंकित कर मुक्त हस्त से मिलाने पर प्राप्त होता है वह अधिक प्रकार का तोरण कहलाता है।
आइए इसे कुछ उदाहरणों से समझने का प्रयास करते है
निम्नलिखित बारंबारता बंटन के लिए कम प्रकार का और अधिक प्रकार का तोरण खींचे।
| वर्ग - अंतराल | 10−20 | 20−30 | 30−40 | 40−50 | 50−60 |
| बारंबारता | 5 | 12 | 8 | 15 | 10 |
दिए गए बंटन का कम प्रकार का और अधिक प्रकार का संचयी बारंबारता बंटन बनाते हैं:
| वर्ग - अंतराल | बारंबारता | संचयी बारंबारता (से कम) | संचयी बारंबारता (से अधिक) |
|---|---|---|---|
| 10−20 | 5 | 5 | 50 |
| 20−30 | 12 | 12+5=17 | 50−5=45 |
| 30−40 | 8 | 17+8=25 | 45−12=33 |
| 40−50 | 15 | 25+15=40 | 33−8=25 |
| 50−60 | 10 | 40+10=50 | 25−15=10 |
स्केल (माप) का चयन :
माना की
X- अक्ष (क्षैतिज अक्ष) पर एक छोटा भाग =1 इकाई
Y- अक्ष (ऊर्ध्वाधर अक्ष) पर एक छोटा भाग =1 इकाई
कम प्रकार का तोरण : हम बिंदुओं [वर्ग-अन्तरालों की ऊपरी सीमा को X- अक्ष (क्षैतिज अक्ष) पर और संगत संचयी बारंबारता (कम प्रकार का) को Y- अक्ष (ऊर्ध्वाधर अक्ष)] (20,5),(30,17),(40,25),(50,40) और (60,50) को ग्राफ पेपर पर अंकित करते है और मुक्त हस्त (free hand) से उन्हें मिलाते है। इस प्रकार से प्राप्त सतत वक्र ही कम प्रकार का तोरण होगा, जिसे नीचे के चित्र में दिखाया गया है।
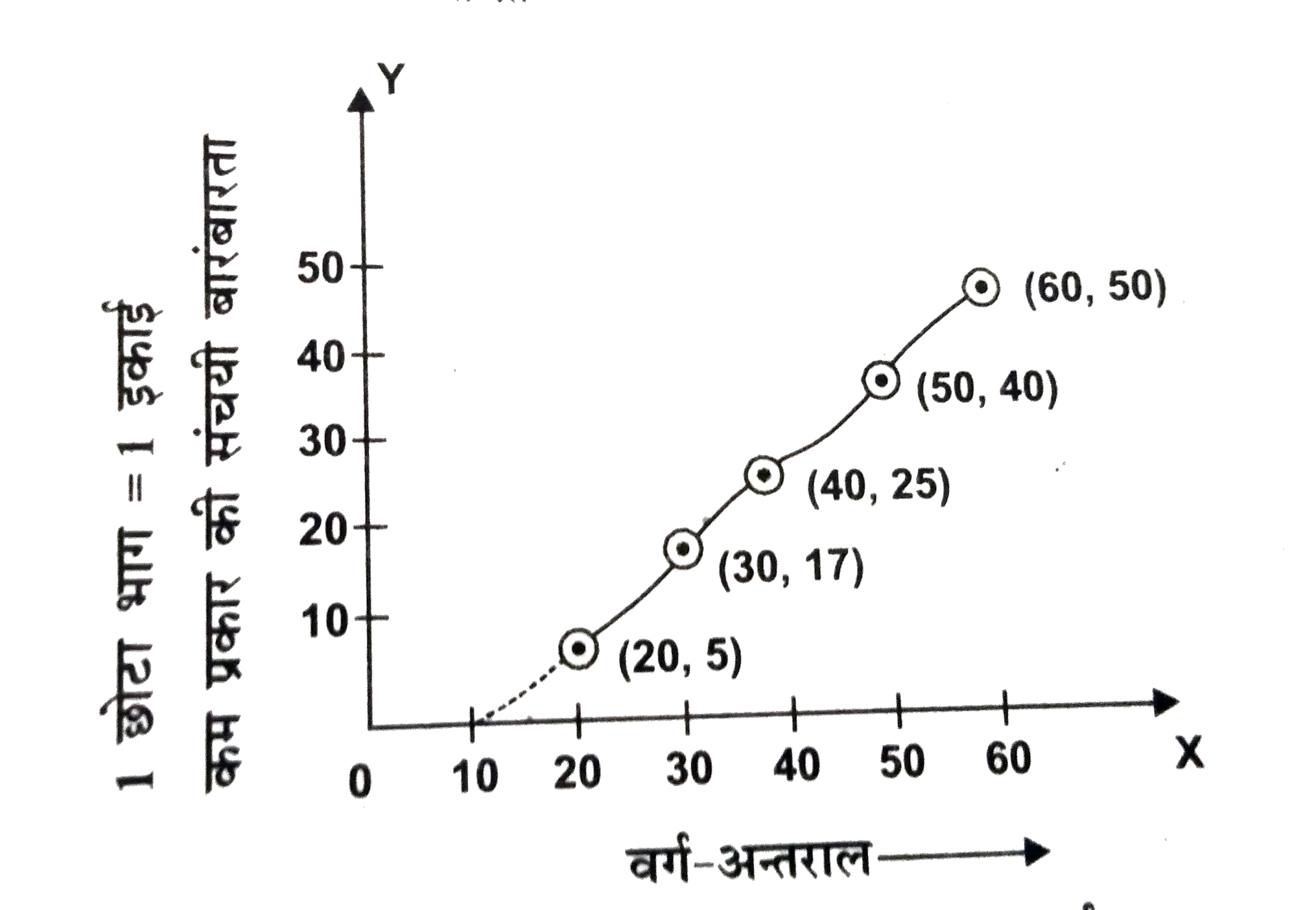
अधिक प्रकार का तोरण : हम बिन्दुओं [वर्ग- अन्तरालों की निम्न सीमा को X - अक्ष पर और संगत संचयी बारंबारता (अधिक प्रकार का) को Y- अक्ष पर] (10,50),(20,45),(30,33),(40,25) और (50,10) को अंकित कर उन्हें मुक्त हस्त से मिला देते हैं। इस प्रकार प्राप्त सतत् वक्र ही अधिक प्रकार का तोरण होगा, जिसे नीचे के चित्र में दिखाया गया है।
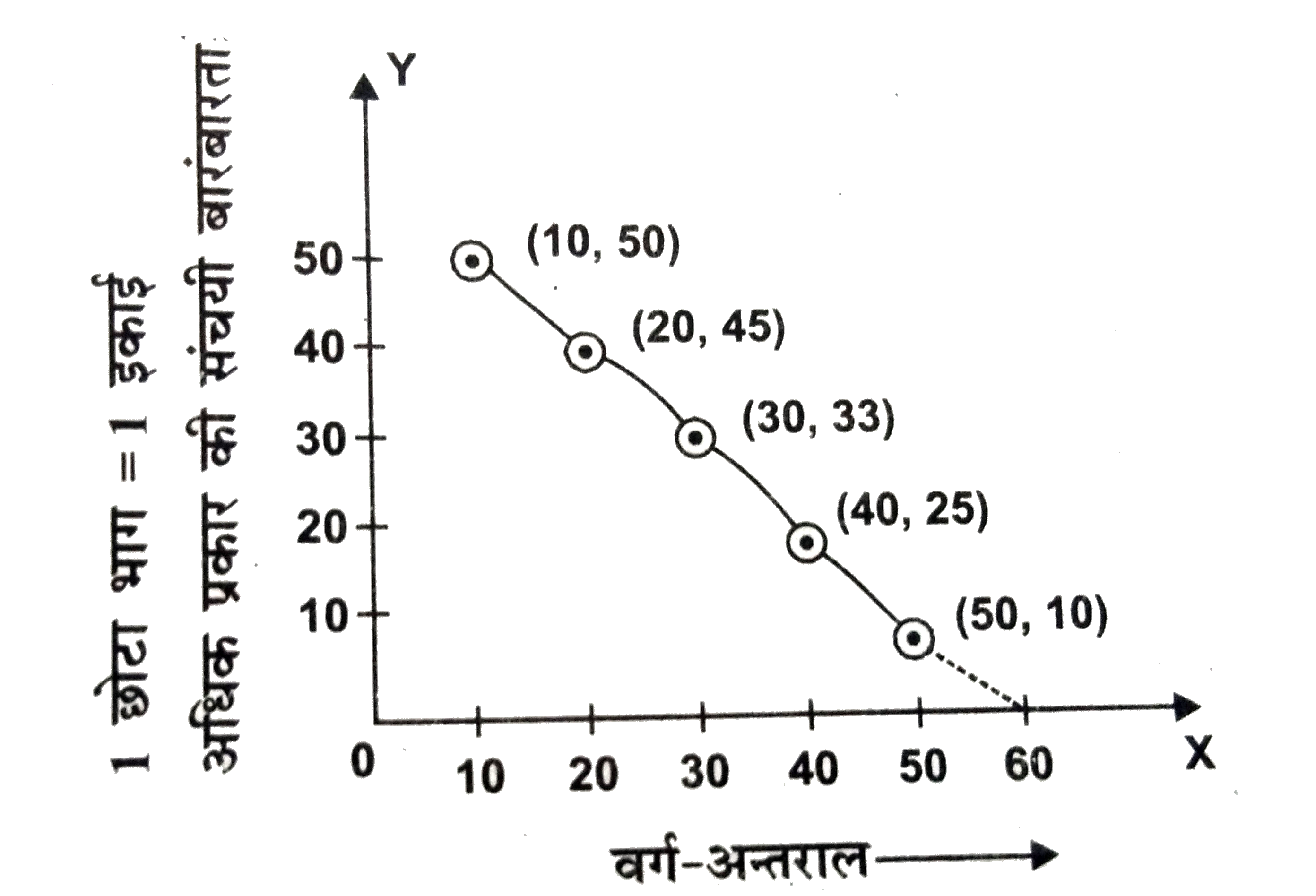
आलेखीय विधि से माध्यक ज्ञात करना :
एक ही ग्राफ पेपर पर कम प्रकार का और अधिक प्रकार का के तोरण खींचे जा सकते हैं।
इसके लिए दोनों तोरणों के प्रतिच्छेद बिंदु से X- अक्ष (क्षैतिज अक्ष) पर लंब डालने पर जो X- अक्ष (क्षैतिज अक्ष) और लंब का प्रतिच्छेद बिंदु है, उसी के संगत मान से माध्यक प्राप्त होता है।
आइए उदाहरण से समझते हैं:
उदाहरण 9
किसी कक्षा के 35 विद्यार्थियों की मेडिकल जांच समय उनके भार निम्नलिखित रूप में रिकॉर्ड किये गए:
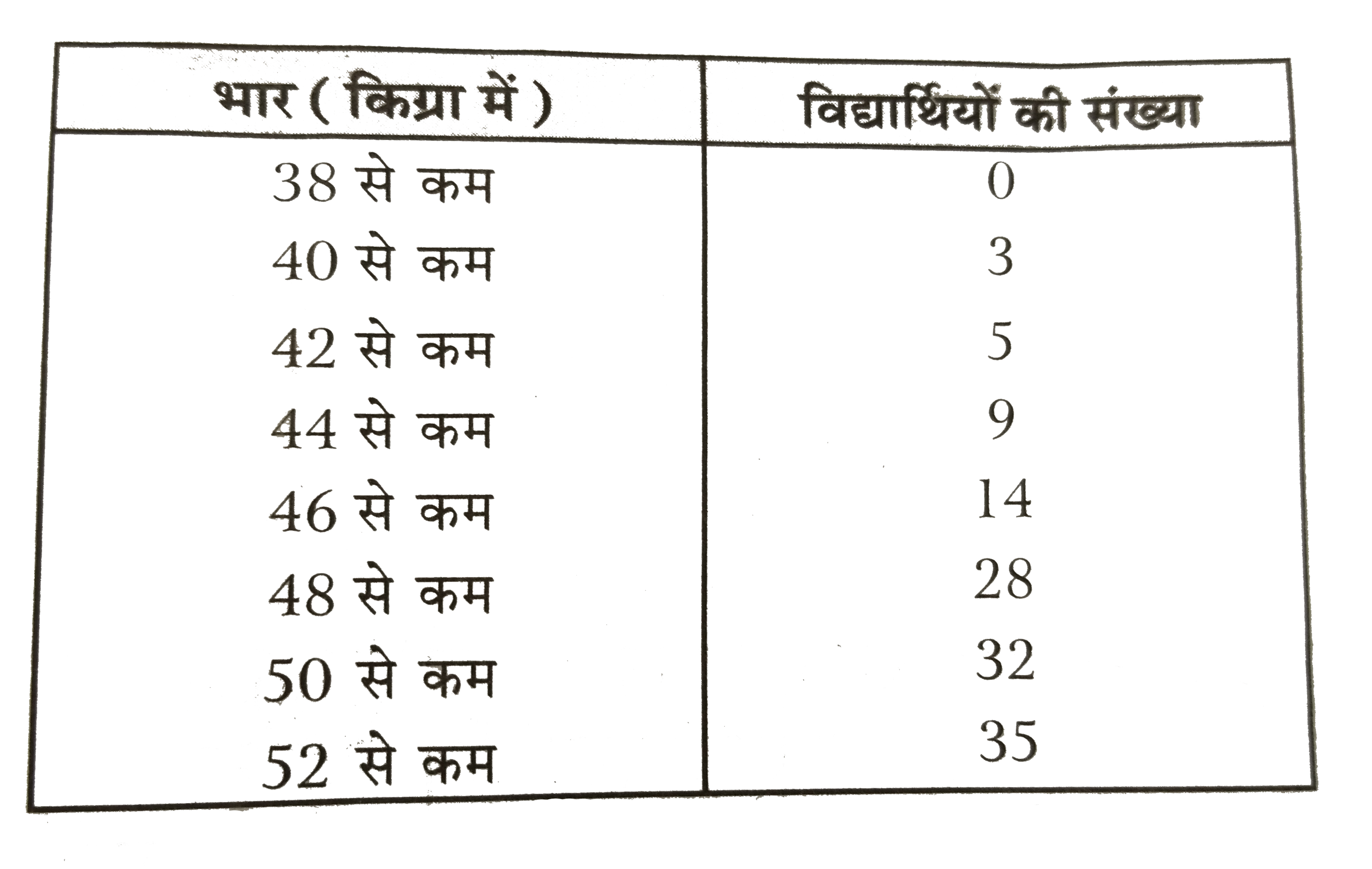
उपरोक्त आंकड़ों के लिए कम प्रकार का तोरण खींचिए इसके बाद माध्यक भार ज्ञात कीजिए।
उपरोक्त बंटन का एक कम प्रकार का संचयी बारंबारता बंटन निम्नलिखित है: 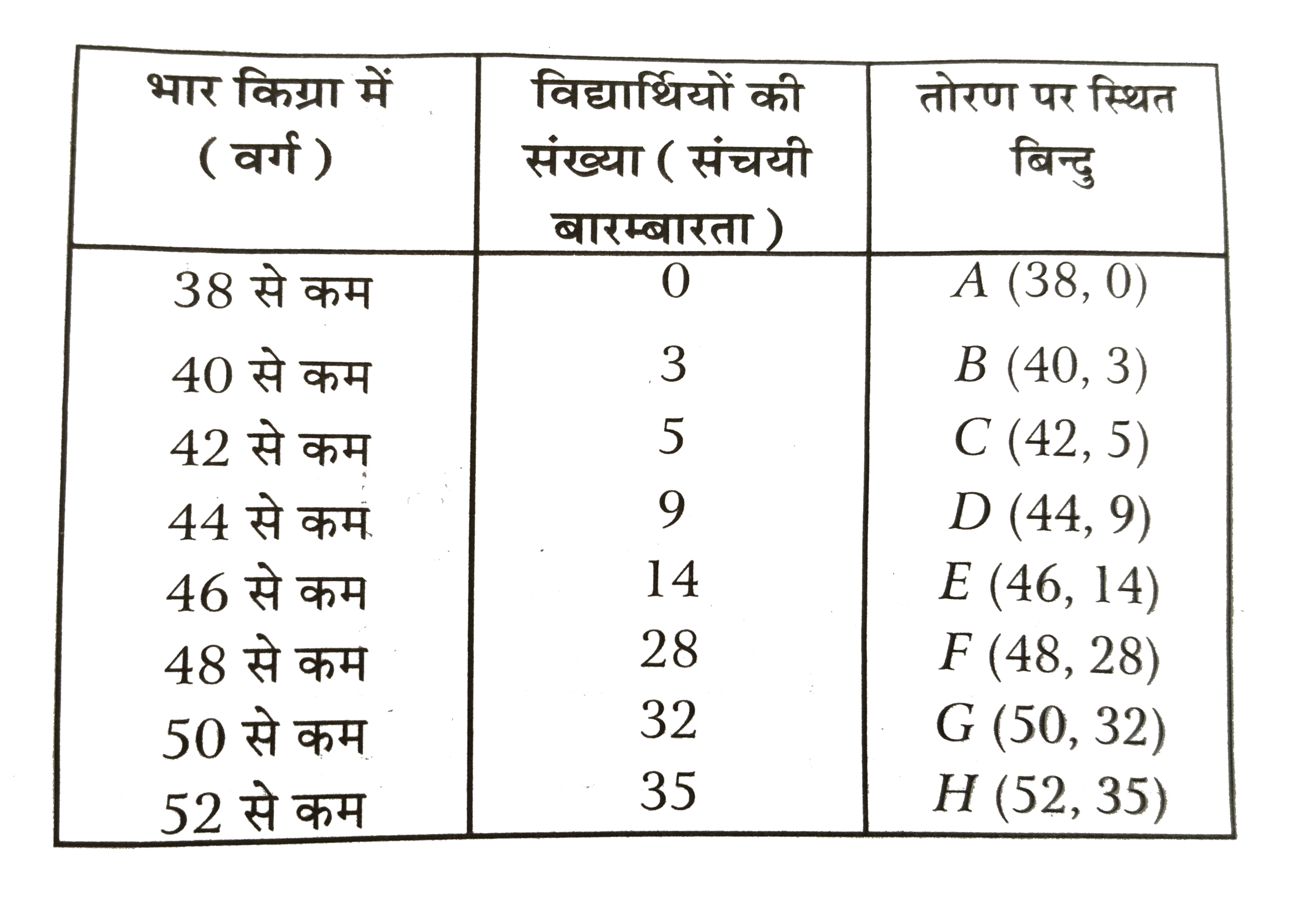
सारणी में दिए आंकड़ों को आलेखीय रूप से निरूपित करने के लिए, हम क्षैतिज अक्ष (X - अक्ष) पर वर्ग अंतरालों की उपरि सीमाएँ एक सुविधाजनक पैमाना (scale) लेकर अंकित करते हैं तथा ऊर्ध्वाधर अक्ष (Y - अक्ष) पर वही या कोई अन्य पैमाना लेकर संचयी बारंबारताएँ अंकित कर, बिंदुओं को मुक्त-हस्त से मिलाते हैं।
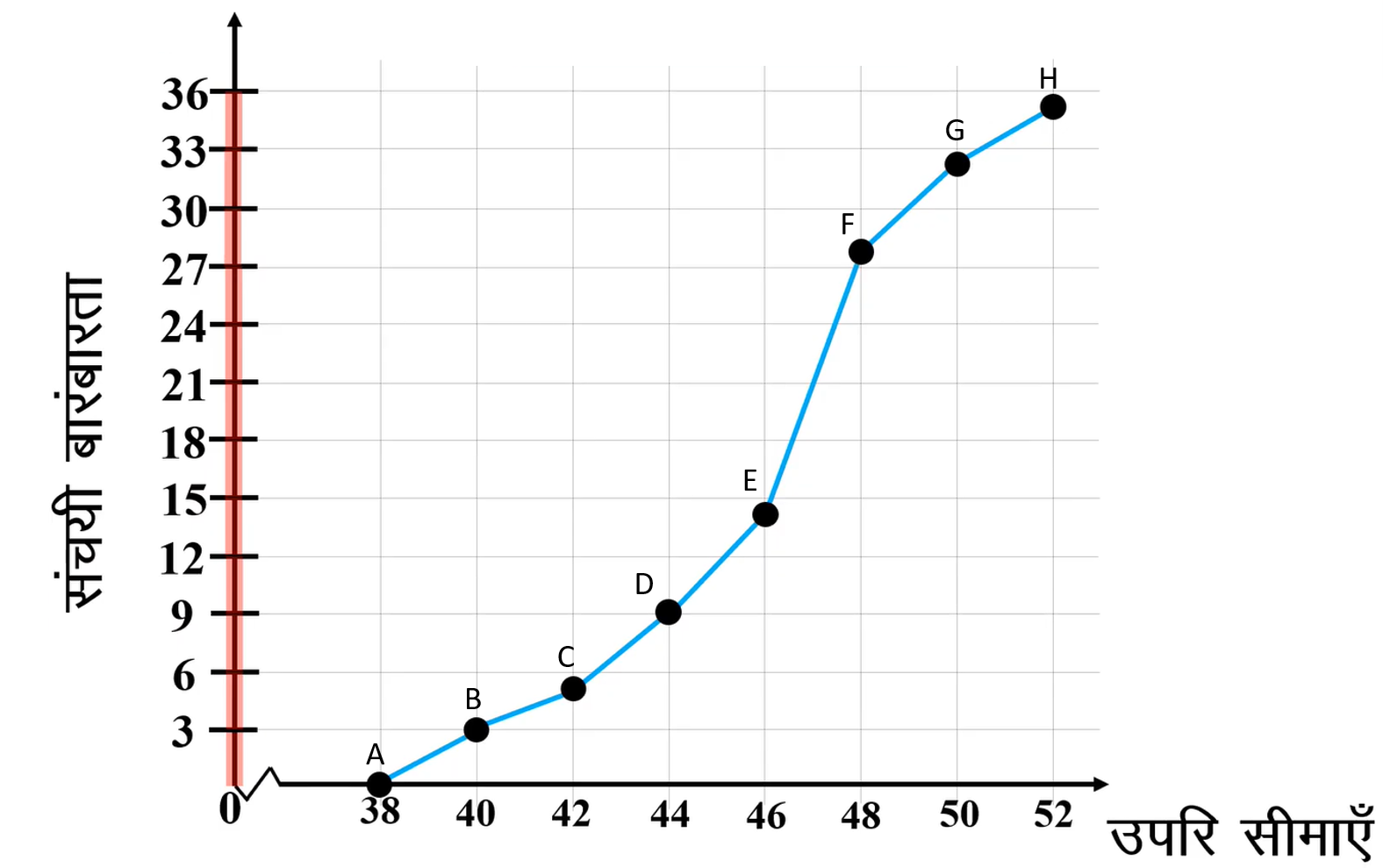
यहाँ n=35⇒n2=17.5
अब Y- अक्ष पर, n2=17.5 की स्थिति ज्ञात कर इस बिंदु से होकर X - अक्ष के समांतर एक रेखा खींचते हैं जो उपरोक्त वक्र को एक बिंदु पर प्रतिच्छेद करती है। इस बिंदु से, X - अक्ष पर लंब डालकर X - अक्ष और इस लंब के प्रतिच्छेद बिंदू से माध्यक निर्धारित हो जाता है।
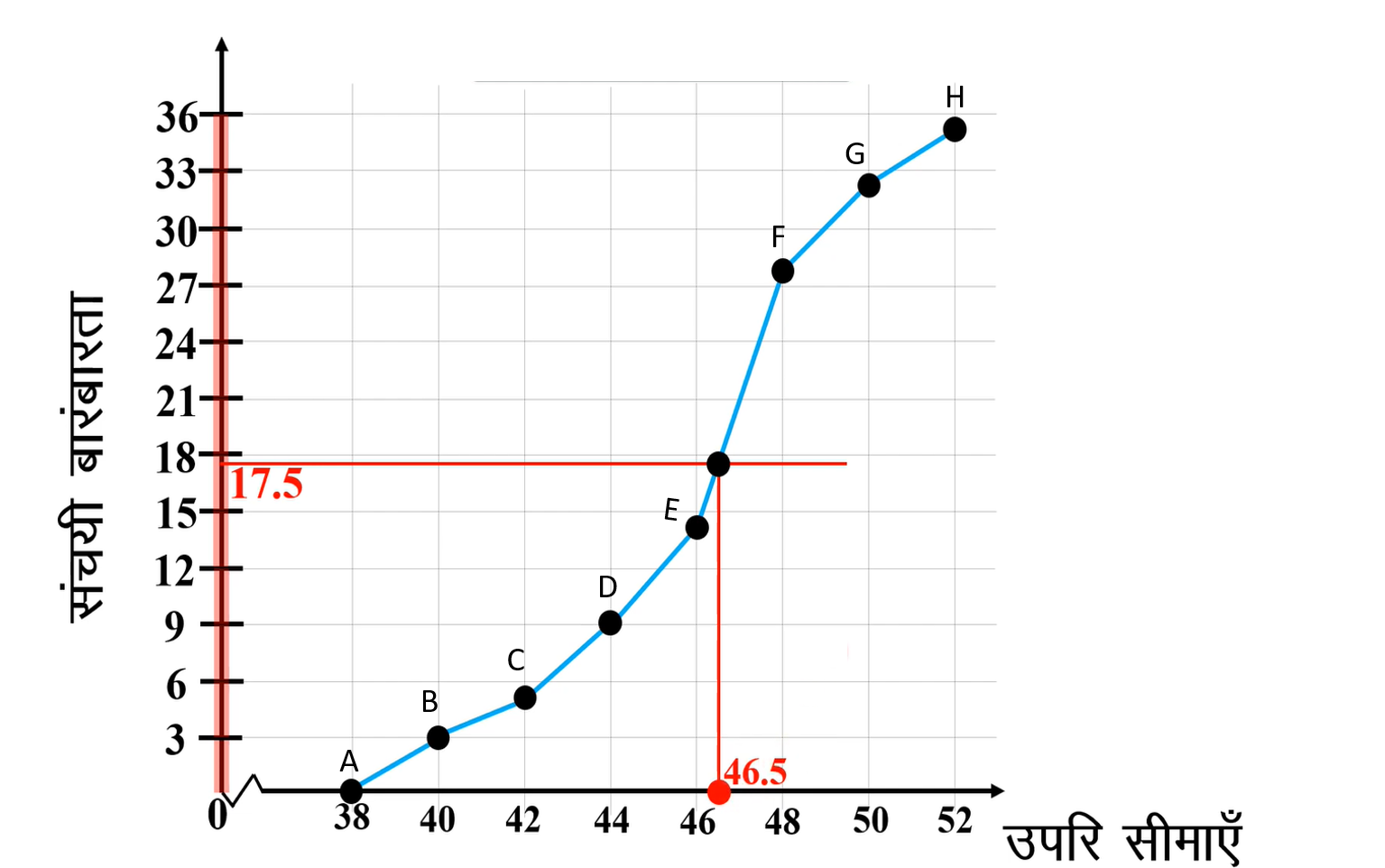
अतः माध्यक भार 46.5 Kg हैं।
उदाहरण 10
निम्नलिखित बारंबारता बंटन के लिए कम प्रकार का और अधिक प्रकार का तोरण खींचे और इससे माध्यक ज्ञात करे।
| वर्ग - अंतराल | 0−4 | 4−8 | 8−12 | 12−16 | 16−20 |
| बारंबारता | 2 | 5 | 7 | 4 | 2 |
"से कम" और "से अधिक" प्रकार का संचयी बारंबारता सारणी बनाते हैं:
| वर्ग - अंतराल | बारंबारता | "से कम प्रकार का" संचयी बारंबारता | "से अधिक प्रकार का" संचयी बारंबारता |
|---|---|---|---|
| 0−4 | 2 | 2 | 20 |
| 4−8 | 5 | 7 | 18 |
| 8−12 | 7 | 14 | 13 |
| 12−16 | 4 | 18 | 6 |
| 16−20 | 2 | 20 | 2 |
अब, बिंदुओं [वर्ग-अन्तरालों की ऊपरी सीमा को X- अक्ष (क्षैतिज अक्ष) पर और संगत संचयी बारंबारता (कम प्रकार का) को Y- अक्ष (ऊर्ध्वाधर अक्ष)] (4,2),(8,7),(12,14),(16,18) और (20,20) को ग्राफ पेपर पर अंकित करते है और मुक्त हस्त (free hand) से उन्हें मिलाते है। इस प्रकार से प्राप्त सतत वक्र "से कम प्रकार का तोरण" होगा
तथा बिंदुओं [वर्ग- अन्तरालों की निम्न सीमा को Y - अक्ष पर और संगत संचयी बारंबारता (अधिक प्रकार का) को Y - अक्ष पर] (0,20),(4,18),(8,13),(12,6) और (16,2) को ग्राफ पेपर पर अंकित करते है और मुक्त हस्त (free hand) से उन्हें मिलाते है। इस प्रकार से प्राप्त सतत वक्र "से अधिक प्रकार का तोरण" होगा।
चित्र में एक उपयुक्त पैमाने की सहायता से बिंदुओं को अंकित किया गया हैं। स्पष्ट हैं की दोनों तोरणों (से अधिक व से कम) के प्रतिच्छेद बिंदु से X- अक्ष (क्षैतिज अक्ष) पर लंब डालने पर जो X- अक्ष (क्षैतिज अक्ष) और लंब का प्रतिच्छेद बिंदु है, उसी के संगत मान से माध्यक प्राप्त होता है।
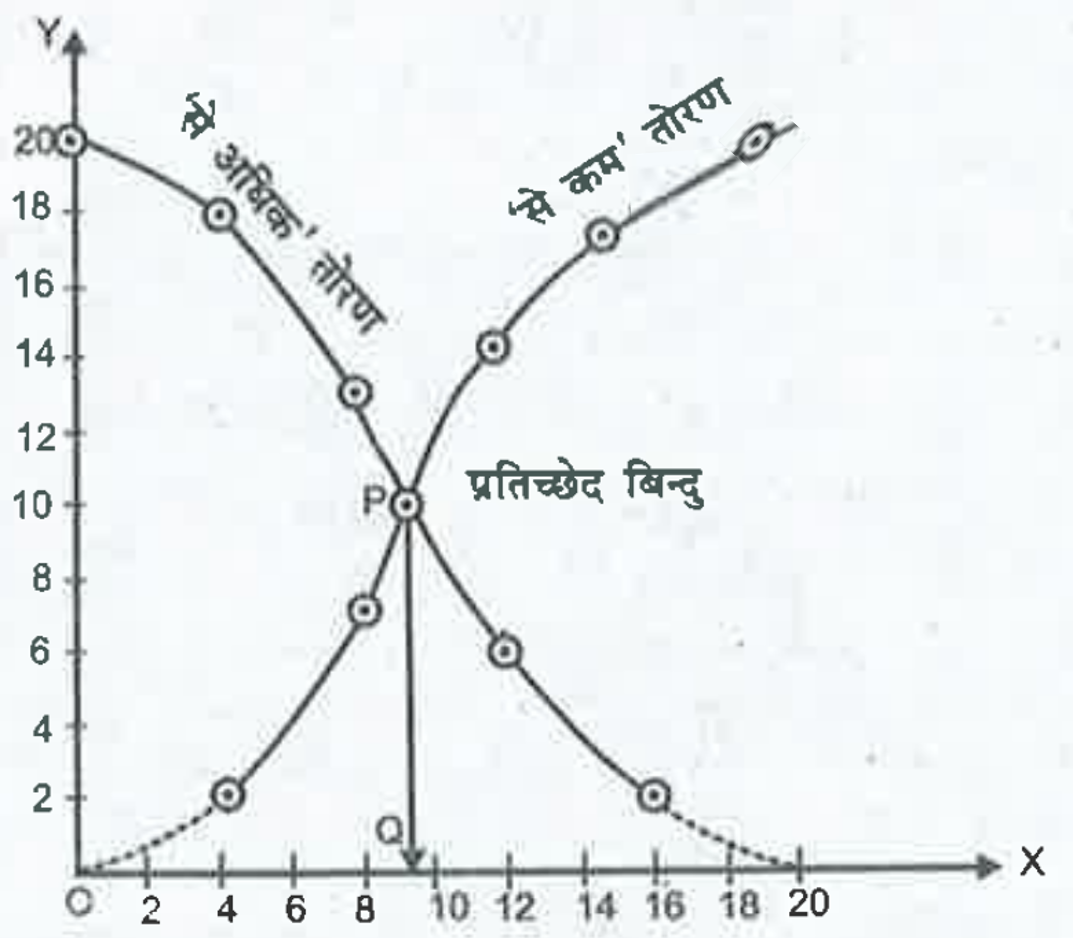
यहाँ माध्यक 9.6 (लगभग) हैं।
सारांश
प्रत्यक्ष विधि : ¯x=∑fixi∑fi
कल्पित माध्य विधि : ¯x=a+∑fidi∑fi, जहाँ di=xi−a
पग - विचलन विधि : ¯x=a+(∑fiui∑fi)×h, जहाँ ui=xi−ah
बहुलक =l+(f1−f02f1−f0−f2)×h
जहाँ
l= बहुलक वर्ग की निम्न सीमा
h= वर्ग अंतराल की माप
f1= बहुलक वर्ग की बारंबारता
f0= बहुलक वर्ग से ठीक पहले के वर्ग की बारंबारता
f1= बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता
माध्यक =l+(n2−cff)×h
जहाँ
l= माध्यक वर्ग की निम्न सीमा
n= प्रेक्षणों की संख्या
cf= माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f= माध्यक वर्ग की बारंबारता
h= माध्यक वर्ग का माप
3 माध्यक = बहुलक +2 माध्य
