Level 2 from ARIHANT PHYSICS Chapter 8 KINEMATICS for Class 11
| Class 11 | PHYSICS |
| Chapter | KINEMATICS |
| ARIHANT PHYSICS | Level 2 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
Two friends A and B are running on a circular track of perimeter equal to 40 m. At time t=0 they are at same location running in the same direction. A is running slowly at a uniform speed of 4.5km/hr whereas B is running swiftly at a speed of 18km/hr.
(a) At what time t0 the two friends will meet again?
(b) What is average velocity of A and B for the interval t=0 to t=t0? View SolutionQuestion 2
A particle is moving along x axis. Its position as a function of time is given by x=x(t). Say whether following statements are true or false.
(a) The particle is definitely slowing down if d2xdt2>0 and dxdt<0
(b) The particle is definitely moving towards the origin if d(x2)dt<0View SolutionQuestion 4
Harshit and Akanksha both can run at speed v and walk at speed u(u<v). They together start on a journey to a place that is at a distance equal to L. Akanksha walks half of the distance and runs the second half. Harshit walks for half of his travel time and runs in the other half. View SolutionQuestion 5
There are two cars on a straight road, marked as x axis. Car A is travelling at a constant speed of VA=9m/s. Let the position of the Car A, at time t=0, be the origin. Another car B is L=40m ahead of car A at t=0 and starts moving at a constant acceleration of a=1m/s2 (at t = 0). Consider the length of the two cars to be negligible and treat them as point objects.

(a) Plot the position–time (x–t) graph for the two cars on the same graph. The two graphs intersect at two points. Draw conclusion from this.
(b) Determine the maximum lead that car A can have. View SolutionQuestion 6
Particle A is moving with a constant velocity of VA=50ms–1 in positive x direction. It crossed the origin at time t=10s. Another particle B started at t=0 from the origin and moved with a uniform acceleration of aB=2ms–2 in positive x direction.
(a) For how long was A ahead of B during the subsequent journey?
(b) Draw the position (x) time (t) graph for the two particles and mark the interval for which A was ahead of B. View SolutionQuestion 7
(a) A particle is moving along the x axis and its velocity vs position graph is as shown. Is the acceleration of the particle increasing, decreasing or remains constant?
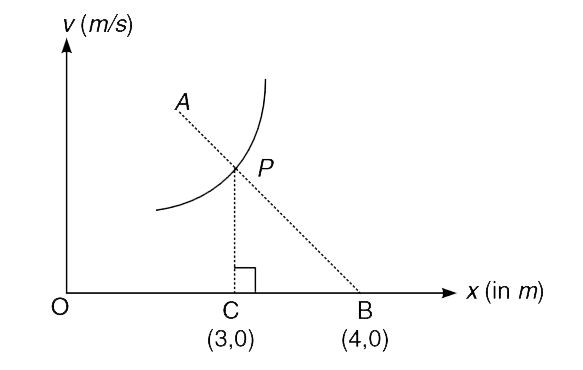
(b) A particle is moving along x axis and its velocity (v) vs position (x) graph is a curve as shown in the figure. Line APB is normal to the curve at point P. Find the instantaneous acceleration of the particle at x=3.0m.
 View Solution
View SolutionQuestion 8
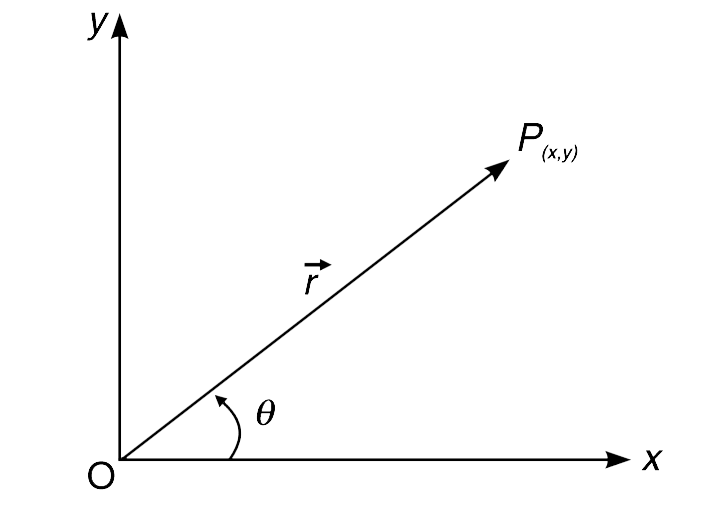
A particle has co-ordinates (x, y). Its position vector makes on angle θ with positive x direction. In an infinitesimally small interval of time the particle moves such that length of its position vector does not change but angle θ increases by dθ. Express the change in position vector of the particle in terms of x, y, dθ and unit vectors ˆi and ˆj.
 View Solution
View SolutionQuestion 9
A rope is lying on a table with one of its end at point O on the table. This end of the rope is pulled to the right with a constant acceleration starting from rest. It was observed that last 2 m length of the rope took 5 s in crossing the point O and the last 1m took 2 s in crossing the point O.

(a) Find the time required by the complete rope to travel past point O.
(b) Find length of the rope. View SolutionQuestion 10

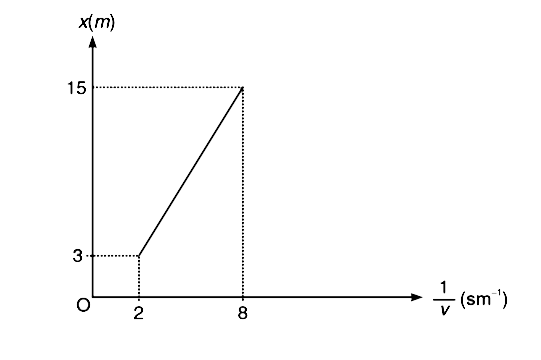
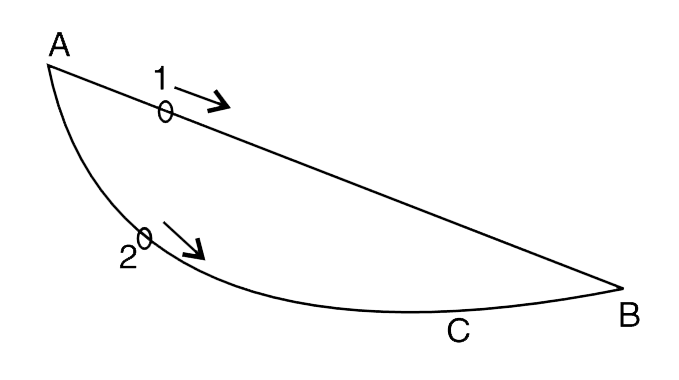
Two particles 1 and 2 move along the x axis. The position (x) - time (t) graph for particle 1 and velocity (v) - time (t) graph for particle 2 has been shown in the figure. Find the time when the two particles collide. Also find the position (x) where they collide. It is given that x0=ut0, and that the particle 2 was at origin at t=0. View SolutionQuestion 11
Two stations A and B are 100km apart. A passenger train crosses station A travelling at a speed of 50km/hr. The train maintains constant speed for 1 hour 48 minute and then the driven applies brakes to stop the train at station B in next 6 minute. Another express train starts from station B at the time the passenger train was crossing station A. The driver of the express train runs the train with uniform acceleration to attain a peak speed v0. Immediately after the train attains the peak speed v0, he applies breaks which cause the train to stop at station A at the same time the passenger train stops at B. Brakes in both the trains cause uniform retardation of same magnitude. Find the travel time of two trains and v0. View SolutionQuestion 12
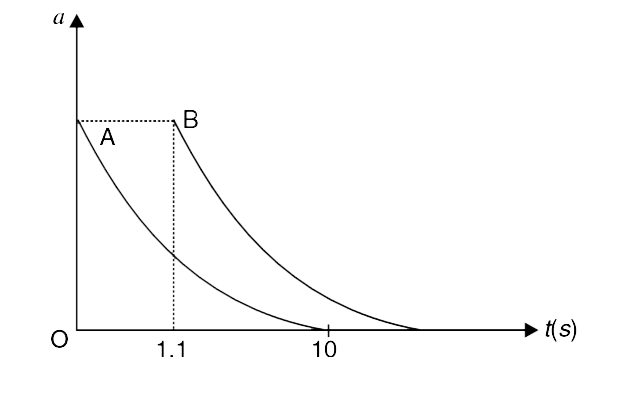
Particle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
 View Solution
View SolutionQuestion 13

A particle is moving in x–y plane. The x and y components of its acceleration change with time according to the graphs given in figure. At time t=0, its velocity is v0 directed along positive y direction. if a0=v0t0, find the angle that the velocity of the particle makes with x axis at time t=4t0. View SolutionQuestion 14
A particle is moving along positive x direction and experiences a constant acceleration of 4m/s2 in negative x direction. At time t=3 second its velocity was observed to be 10m/s in positive x direction.
(a) Find the distance travelled by the particle in the interval t=0 to t=3s. Also find distance travelled in the interval t=0 to t=7.5s..
(b) Plot the displacement – time graph for the interval t=0 to 7.5s. View SolutionQuestion 15
A bead moves along a straight horizontal wire of length L, starting from the left end with velocity v0. Its retardation is proportional to the distance that remains to the right end of the wire. Find the initial retardation (at left end of the wire) if the bead reaches the right end of the wire with a velocity v02.View SolutionQuestion 16
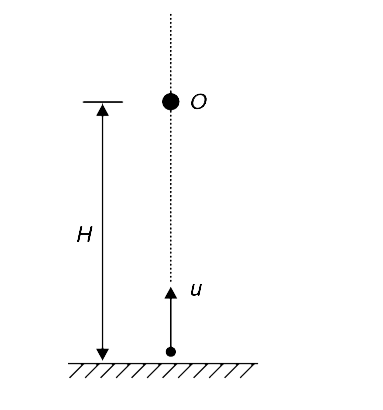
A ball is projected vertically up from the ground surface with an initial velocity of u=20m/s. O is a fixed point on the line of motion of the ball at a height of H=15m from the ground. Plot a graph showing variation of distance (s) of the ball from the fixed point O, with time (t). [Take g=10m/s2]. Plot the graph for the entire time of flight of the ball.
 View Solution
View SolutionQuestion 17
Two bodies 1 and 2 of different shapes are released on the surface of a deep pond. The mass of the two bodies are m1=1kg and m2=1.2kg respectively. While moving through water, the bodies experience resistive force given as R=bv, where v is speed of the body and b is a positive constant dependent on shape of the body. For bodies 1 and 2 value of b is 2.5kg/s and 3.0kg/s respectively. Neglect all other forces apart from gravity and the resistive force, while answering following questions : [Hint : acceleration =force/mass]
(i) With what speed v10 and v20 will the two bodies hit the bed of the pond. [Take g=10m/s2]
(ii) Which body will acquire speed equal to half the terminal speed in less time. View SolutionQuestion 18
A prototype of a rocket is fired from the ground. The rocket rises vertically up with a uniform acceleration of 54m/s2. 8 second after the start a small nut gets detached from the rocket. Assume that the rocket keeps rising with the constant acceleration.
(a) What is the height of the rocket at the instant the nut lands on the ground
(b) Plot the velocity – time graph for the motion of the nut after it separates from the rocket till it hits the ground. Plot the same velocity– time graph in the reference frame of the rocket. Take vertically upward direction as positive and g=10m/s2 View SolutionQuestion 19
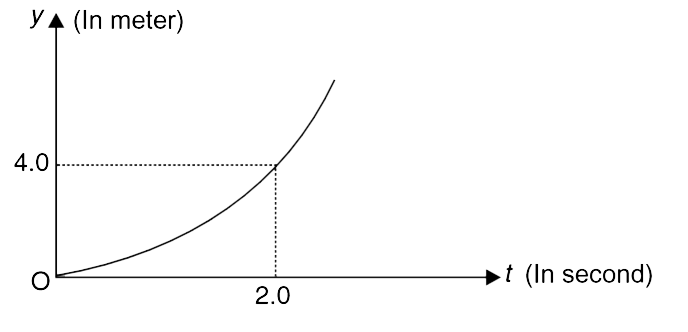
An elevator starts moving upward with constant acceleration. The position time graph for the floor of the elevator is as shown in the figure. The ceiling to floor distance of the elevator is 1.5 m. At t=2.0s, a bolt breaks loose and drops from the ceiling.
(a) At what time t0 does the bolt hit the floor?
(b) Draw the position time graph for the bolt starting from time t=0. [take g=10m/s2]
 View Solution
View SolutionQuestion 20
At t=0 a projectile is projected vertically up with a speed u from the surface of a peculiar planet. The acceleration due to gravity on the planet changes linearly with time as per equation g=αt where α is a constant.
(a) Find the time required by the projectile to attain maximum height.
(b) Find maximum height attained.
(c) Find the total time of flight. View SolutionQuestion 21
A wet ball is projected horizontally at a speed of u=10m/s from the top of a tower h=31.25m high. Water drops detach from the ball at regular intervals of Δt=1.0s after the throw.
(a) How many drops will detach from the ball before it hits the ground.
(b) How far away the drops strike the ground from the point where the ball hits the ground? View SolutionQuestion 22
Two stones of mass m and M(M>m) are dropped Δt time apart from the top of a tower. Take time t=0 at the instant the second stone is released. Let Δv and Δs be the difference in their speed and their mutual separation respectively. Plot the variation of Δv and Δs with time for the interval both the stones are in flight. [g=10m/s2]View SolutionQuestion 23
A particle is moving in the xy plane on a sinusoidal course determined by y = A sin kx, where k and A are constants. The X component of the velocity of the particle is constant and is equal to v0 and the particle was at origin at time t=0. Find the magnitude of the acceleration of the particle when it is at point having x co ordinate x=π2k.View SolutionQuestion 24
A ball is projected from a cliff of height h=19.2 m at an angle a to the horizontal. It hits an incline passing through the foot of the cliff, inclined at an angle θ to the horizontal. Time of flight of the ball is T=2.4s. Foot of the cliff is the origin of the co-ordinate system, horizontal is x direction and vertical is y direction (see figure). Plot of y co-ordinate vs time and y component of velocity of the ball (vy) vs its x co-ordinate (x) is as shown. x and y are in m and time is in s in the graph. [g=10m/s2]
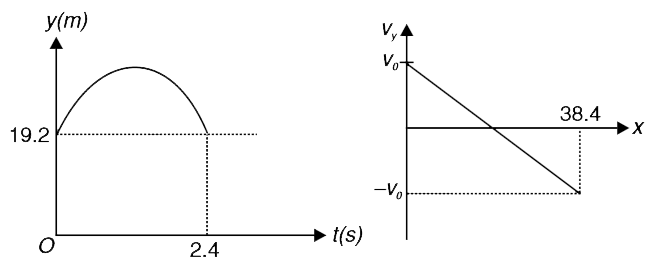
(a) Find the angle of projection a
(b) Find the inclination (θ) of the incline.
(c) If the ball is projected with same speed but at an angle θ(= inclination of incline) to the horizontal, will it hit the incline above or below the point where it struck the incline earlier? View SolutionQuestion 25
A canon can fire shells at speed u. Inclination of its barrel to the horizontal can be changed in steps of Δθ=1∘ ranging from θ1=15∘ to θ2=85∘. Let Rn be the horizontal range for projection angle θ=n∘.
ΔRn=|Rn−Rn+1|
For what value of n the value of ΔRn is maximum? Neglect air resistance.
(ii) A small water sprinkler is in the shape of a hemisphere with large number of uniformly spread holes on its surface. It is placed on ground and water comes out of each hole with speed u. Assume that we mentally divide the ground into many small identical patches – each having area ΔS. What is the distance of a patch from the sprinkler which receives maximum amount of water ?View SolutionQuestion 26
A gun fires a large number of bullets upward. Due to shaking of hands some bullets deviate as much as 1° from the vertical. The muzzle speed of the gun is 150m/s and the height of gun above the ground is negligible. The radius of the head of the person firing the gun is 10cm. You can assume that acceleration due to gravity is nearly constant for heights involved and its value is g=10m/s2. The gun fires 1000 bullets and they fall uniformly over a circle of radius r. Neglect air resistance. You can use the fact sinθ≅θ when θ is small.
(a) Find the approximate value of r. (b) What is the probability that a bullet will fall on the person’s head who is firing? View SolutionQuestion 27
Three stones are projected simultaneously with same speed u from the top of a tower. Stone 1 is projected horizontally and stone 2 and stone 3 are projected making an angle q with the horizontal as shown in fig. Before stone 3 hits the ground, the distance between 1 and 2 was found to increase at a constant rate u.
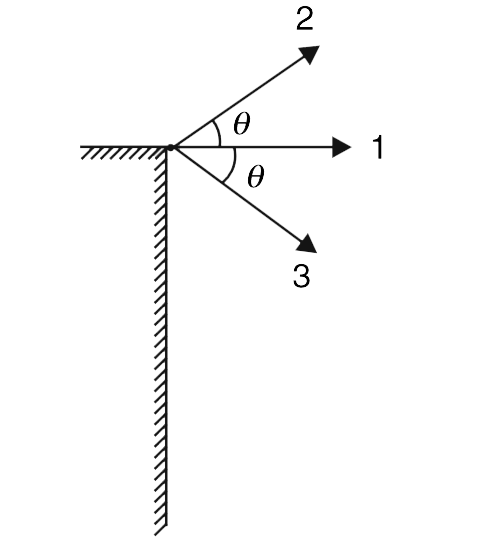
(a) Find θ
(b) Find the rate at which the distance between 2 and 3 increases. View SolutionQuestion 29
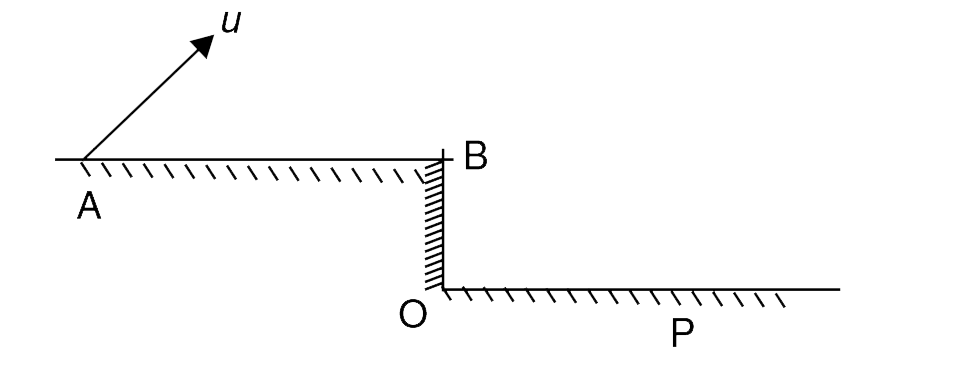
A wall OP is inclined to the horizontal ground at an angle α. Two particles are projected from points A and B on the ground with same speed (u) in directions making an angle θ to the horizontal (see figure). Distance between points A and B is x0=24m. Both particles hit the wall elastically and fall back on the ground. Time of flight (time required to hit the wall and then fall back on to the ground) for particles projected from A and B are 4 s and 2 s respectively. Both the particles strike the wall perpendicularly and at the same location. [In elastic collision, the velocity component of the particle that is perpendicular to the wall gets reversed without change in magnitude]
(a) Calculate maximum height attained by the particle projected from A.

(b) Calculate the inclination of the wall to the horizontal (α)[g=10m/s2] View SolutionQuestion 30
AB is a pipe fixed to the ground at an inclination of 37°. A ball is projected from point O at a speed of u=20m/s at an angle of 53° to the horizontal and it smoothly enters into the pipe with its velocity parallel to the axis of the pipe. [Takeg=10ms–2]

(a) Find the length L of the pipe
(b) Find the distance of end B of the pipe from point O. View SolutionQuestion 31
(a) A boy throws several balls out of the window of his house at different angles to the horizontal. All balls are thrown at speed u=10m/s and it was found that all of them hit the ground making an angle of 45° or larger than that with the horizontal. Find the height of the window above the ground [take g=10m/s2]
(b) A gun is mounted on an elevated platform AB. The distance of the gun at A from the edge B is AB=960m. Height of platform is OB=960m. The gun can fire shells with a velocity of u=100m/s at any angle. What is the minimum distance (OP) from the foot of the platform where the shell of gun can reach ?
 View Solution
View SolutionQuestion 32
An object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s
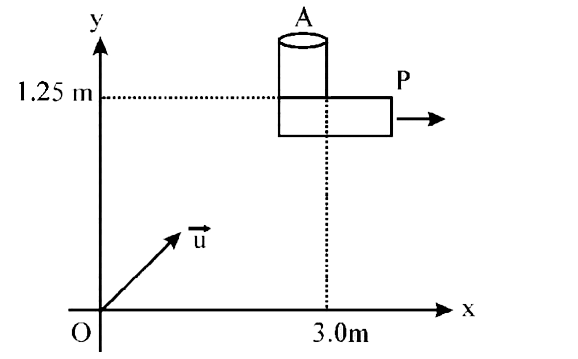 View Solution
View SolutionQuestion 33
(a) A particle is thrown from a height h horizontally towards a vertical wall with a speed v as shown in the figure. If the particle returns to the point of projection after suffering two elastic collisions, one with the wall and another with the ground, find the total time of flight. [Elastic collision means the velocity component perpendicular to the surface gets reversed during collision.]
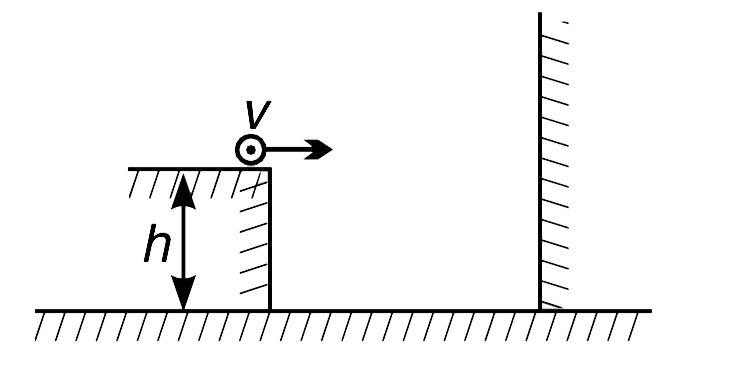
(b) Touching a hemispherical dome of radius R there is a vertical tower of height H=4R. A boy projects a ball horizontally at speed u from the top of the tower. The ball strikes the dome at a height R2 from ground and rebounds. After rebounding the ball retraces back its path into the hands of the body. Find u.
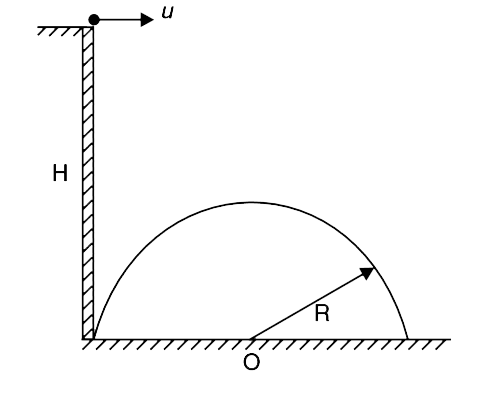 View Solution
View SolutionQuestion 34
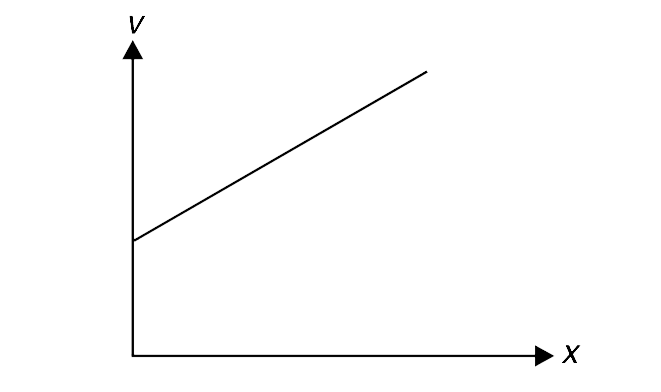
A city bus has a horizontal rectangular roof and a rectangular vertical windscreen. One day it was raining steadily and there was no wind.
(a) Will the quantity of water falling on the roof in unit time be different for the two cases (i) the bus is still (ii) the bus is moving with speed v on a horizontal road ?
(b) Draw a graph showing the variation of quantity of water striking the windscreen in unit time with speed of the bus (v)View SolutionQuestion 35
A truck is travelling due north descending a hill of slope angle θ=tan–1(0.1) at a constant speed of 90km/hr. At the base of the hill there is a gentle curve and beyond that the road is level and heads 30∘ east of north. A south bound police car is travelling at 80km/hr along the level road at the base of the hill approaching the truck. Find the velocity of the truck relative to police car in terms of unit vectors ˆi,ˆj and ˆk . Take x axis towards east, y axis towards north and z axis vertically upwards. View SolutionQuestion 36
Two persons A and B travelling at 60km/hr–1 in their cars moving in opposite directions on a straight road observe an airplane. To the person A, the airplane appears to be moving perpendicular to the road while to the observe B the plane appears to cross the road making an angle of 45°.
(a) At what angle does the plane actually cross the road (relative to the ground).
(b) Find the speed of the plane relative to the ground.View SolutionQuestion 37
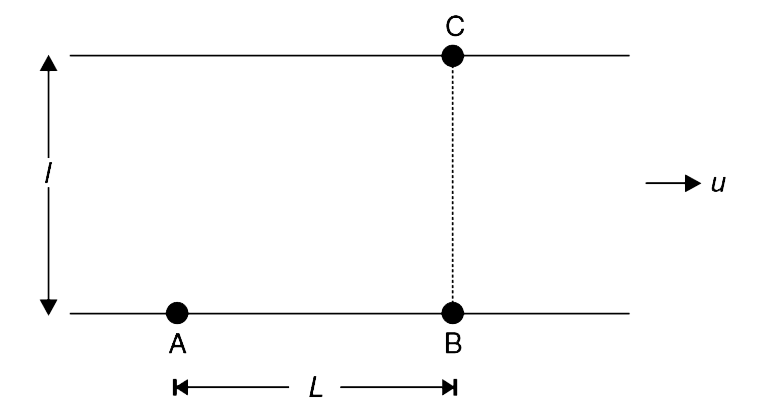
Two friends A and B are standing on a river bank L distance apart. They have decided to meet at a point C on the other bank exactly opposite to B. Both of them start rowing simultaneously on boats which can travel with velocity V=5km/hr in still water. It was found that both reached at C at the same time. Assume that path of both the boats are straight lines. Width of the river is l=3.0km and water is flowing at a uniform speed of u=3.0km/hr.
(a) In how much time the two friends crossed the river.
(b) Find L. View SolutionQuestion 38
On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x−aξsandithitsthetrol≤y.<br>(a)Themotionoftheballisobservedomtheameofthetrol≤y.Calca––tethe∠thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).
 View Solution
View SolutionQuestion 39
A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .
 View Solution
View SolutionQuestion 40
A ball is projected in vertical x–y plane from a car moving along horizontal x direction. The car is speeding up with constant acceleration. Which one of the following trajectory of the ball is not possible in the reference frame attached to the car? Give reason for your answer. Explain the condition in which other trajectories are possible. Consider origin at the point of projection.
 View Solution
View SolutionQuestion 41
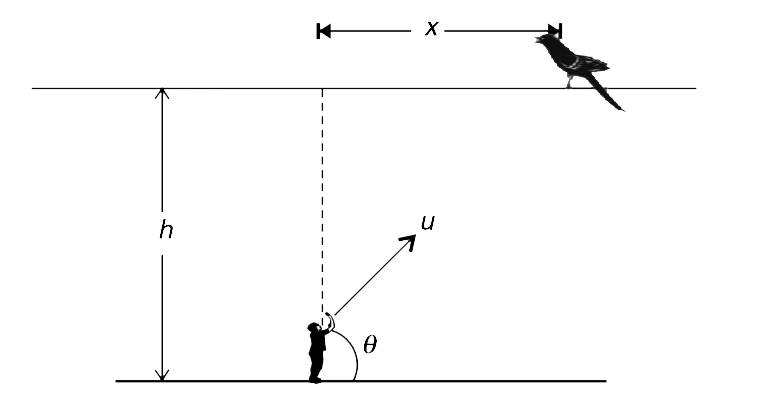
A boy standing on a cliff 50 m high throws a ball with speed 40m/s directly aiming towards a man standing on ground at B. At the same time the man at B throws a stone with a speed of 10m/s directly aiming towards the boy.
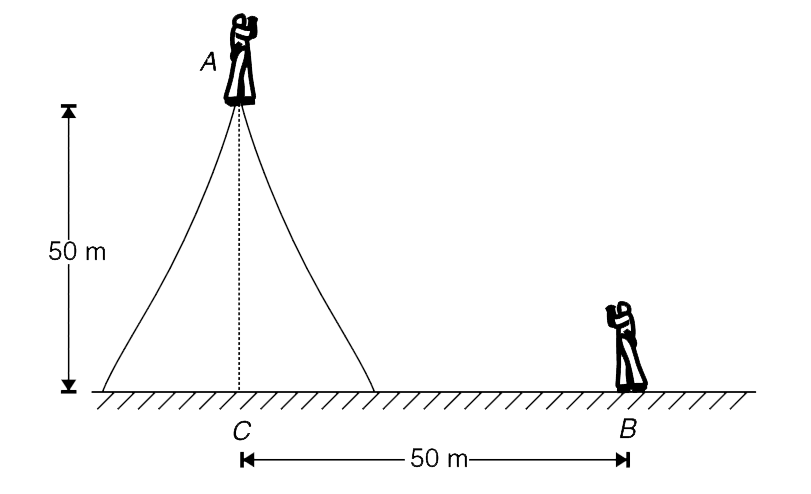
(a) Will the ball and the stone collide? If yes, at what time after projection?
(b) At what height above the ground the two objects collide?
(c) Draw the path of ball in the reference frame of the stone. View SolutionQuestion 42
A man walking downhill with velocity V0 finds that his umbrella gives him maximum protection from rain when he holds it such that the stick is perpendicular to the hill surface. When the man turns back and climbs the hill with velocity V0, he finds that it is most appropriate to hold the umbrella stick vertical. then the actual speed of raindrops in terms of V0 is : (the inclination of the hill is θ=37∘)
 View Solution
View SolutionQuestion 43
There are two hills A and B and a car is travelling towards hill A along the line joining the two hills. Car is travelling at a constant speed u. There is a wind blowing at speed u in the direction of motion of the car (i.e., from hill B to A). When the car is at a distance x1 from A and x2 from B it sounds horn (for very short interval). Driver hears the echo of horn from both the hills at the same time.
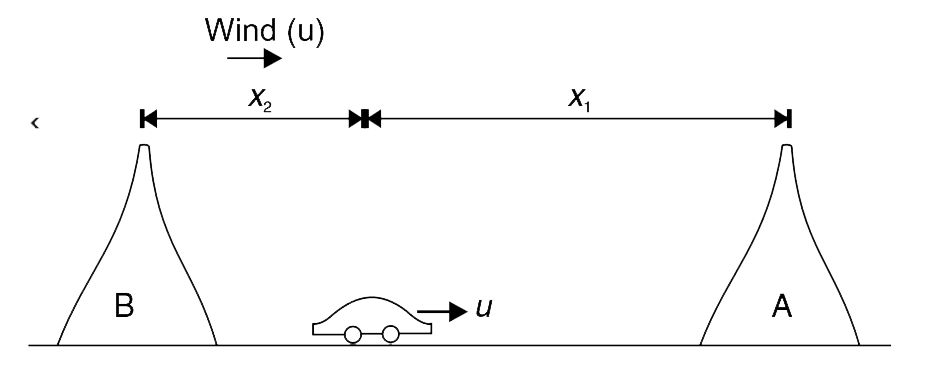
Find the ratio x1x2 taking speed of sound in still air to ve V. View SolutionQuestion 44
The figure shows a square train wagon ABCD which has a smooth floor and side length of 2 L. The train is mov- ing with uniform acceleration (a) in a direction parallel to DA. A 'ball is rolled along the floor with a veloci- ty u, parallel to AB, with respect to the wagon. The ball passes through the centre of the wagon floor. At the instant it is at the centre, brakes are CD AB u 2 L 2 Lapplied and the train begins to retard at a uniform rate that is equal to its previous acceleration (a)
(a) Will the ball hit the wall BC or wall CD or the corner C?
(b) What is speed of the ball, relative to the wagon at the instant it hits a wall ?
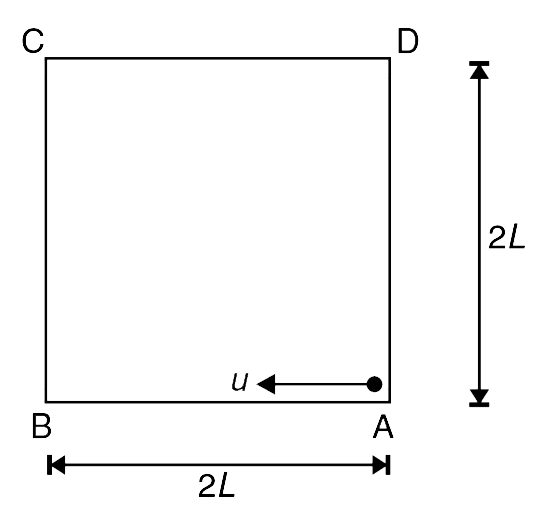 View Solution
View SolutionQuestion 45
Five particles are projected simultaneously from the top of a tower that is h=32m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal.
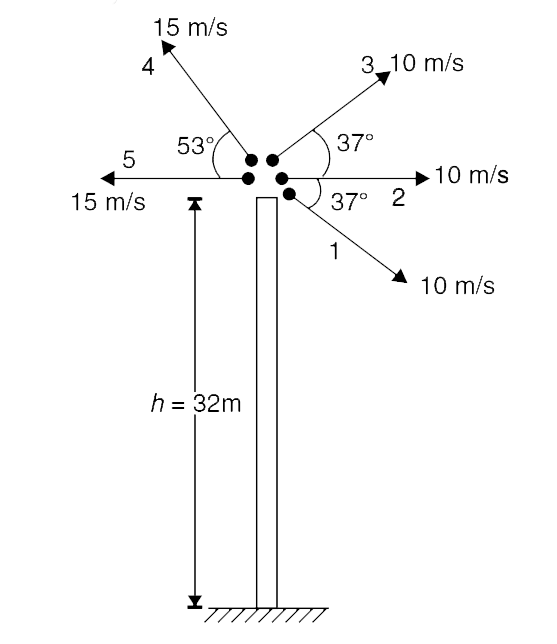
(a) Which particle will hit the ground first?
(b) Separation between which two particles is maximum at the instant the first particle hits the ground?
(c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground.
[g=10m/s2,tan37∘=34] View SolutionQuestion 46
From the top of a long smooth incline a small body A is projected along the surface with speed u. Simultaneously, another small object B is thrown horizontally with velocity v=10m/s, from the same point. The two bodies travel in the same vertical plane and body B hits body A on the incline. If the inclination angle of the incline is θ=cos−1(45) find
(a) the speed u with which A was projected.
(b) the distance from the point of projection, where the two bodies collide.
 View Solution
View SolutionQuestion 47
A man is on straight road AC, standing at A. He wants to get to a point P which is in field at a distance ‘d’ off the road (see figure). Distance AB is l=50. The man can run on the road at a speed v1=5m/s and his speed in the field is v2=3m/s.

(a) Find the minimum value of ‘d’ for which man can reach point P in least possible time by travelling only in the field along the straight line AP.
(b) If value of ‘d’ is half the value found in (a), what length the man must run on the road before entering the field, in order to reach ‘P’ in least possible time. View SolutionQuestion 48
Two particles, A and B are moving in concentric circles in anticlockwise sense in the same plane with radii of the circles being γA=1.0m and γB=2.0m respectively. The particles move with same angular speed of ω=4rad/s. Find the angular velocity of B as observed by A if
(a) Particles lie on a line passing through the centre of the circle.
(b) Particles lie on two perpendicular lines passing through the centre. View SolutionQuestion 49
(a) An unpowered rocket is in flight in air. At a moment the tracking radar gives following data regarding the rocket. r = distance of the rocket from the radar = 4000m,drdt=0,dθdt=1.8deg/sec, where θ is the angle made by position vector of the rocket with respect to the vertical.
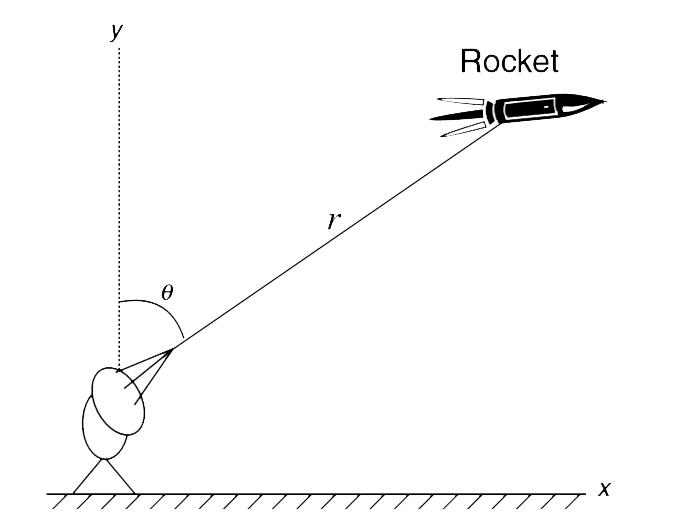
(a) Neglect atmospheric resistance and take g=9.8m/s2 at the concerned height. Neglect height of radar. Calculate the height of the rocket above the ground.
(b) Two points A and B are moving in X - Y plane with constant velocity of VA=(6ˆi−9ˆj)m/s and VB=(ˆi+ˆj)m/s respectively. At time t=0 they are 15 m apart and both of them lie on y axis with A lying away on positive Y axis with respect to B. What is the angular velocity of A with respect to B at t=1s? View SolutionQuestion 50
A stone is projected horizontally with speed u from the top of a tower of height h.
(a) Calculate the radius of curvature of the path of the stone at the point where its tangential and radial accelerations are equal.
(b) What shall be the height (h) of the tower so that radius of curvature of the path is always less than the value obtained in (a) above. View SolutionQuestion 51
A stick of length L=2.0m is leaned against a wall as shown. It is released from a position when θ=60∘. The end A of the stick remains in contact with the wall and its other end B remains in contact with the floor as the stick slides down. Find the distance travelled by the centre of the stick by the time it hits the floor.
 View Solution
View SolutionQuestion 52
(a) A line PQ is moving on a fixed circle of radius R. The line has a constant velocity v perpendicular to itself. Find the speed of point of intersection (A) of the line with the circle at the moment the line is at a distance d=R/2 from the centre of the circle.
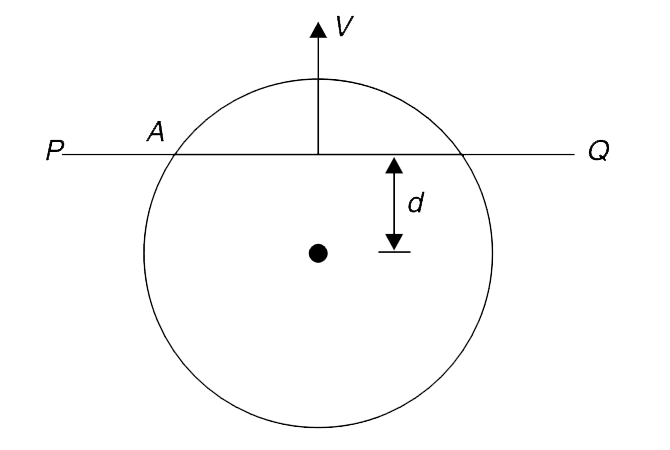
(b) In the figure shown a pin P is confined to move in a fixed circular slot of radius R. The pin is also constrained to remains inside the slot in a straight arm O'A. The arm moves with a constant angular speed w about the hinge O'. What is the acceleration of point P ?
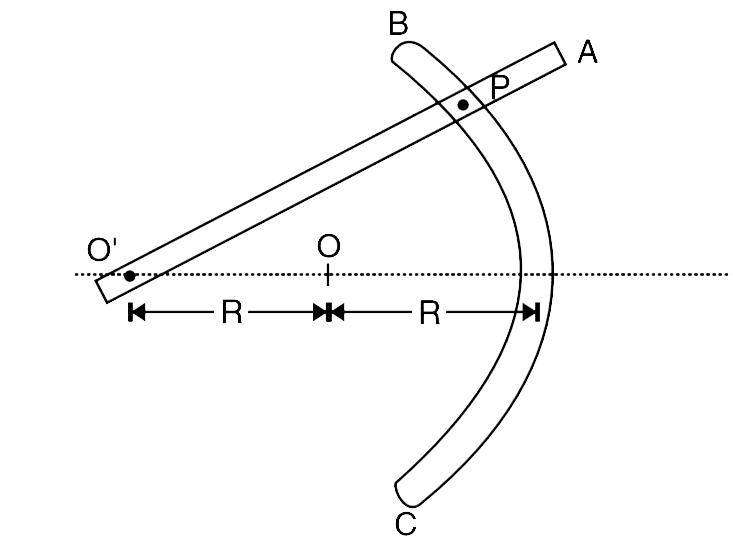 View Solution
View SolutionQuestion 53
A flexible inextensible cord supports a mass M as shown in figure. A1,A2 and B are small pulleys in contact with the cord. At time t=0 cord PQ is horizontal and A1,A2 start moving vertically down at a constant speed of v1, whereas B moves up at a constant speed of v2. Find the velocity of mass M as a function of time.
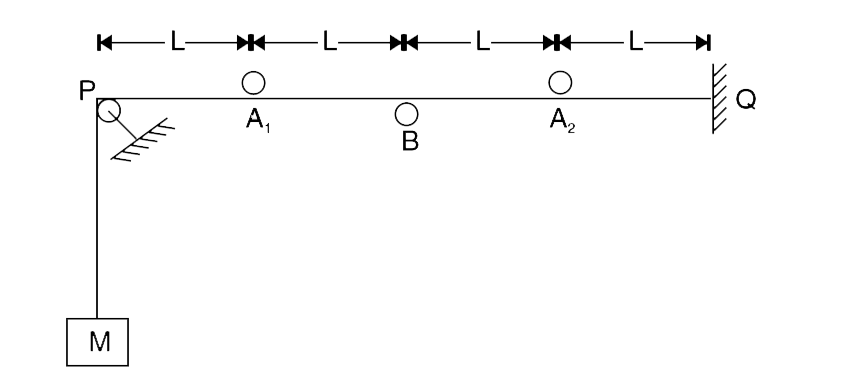 View Solution
View SolutionQuestion 55
A meter stick AB is lying on a horizontal table. Its end A is pulled up so as to move it with a constant velocity VA=4ms–1 along a vertical line. End B slides along the floor.

(a) After how much time (t0) speed (VB) of end B becomes equal to the speed (VA) of end A ?
(b) Find distance travelled by the end B in time t0.View SolutionQuestion 56
One end of a rope is fixed at a point on the ceiling the other end is held close to the first end so that the rope is folded. The second end is released from this position. Find the speed at which the fold at F is descending at the instant the free end of the rope is going down at speed V.
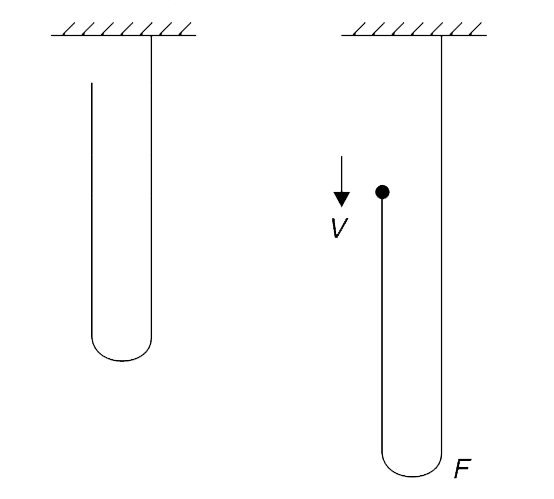 View Solution
View SolutionQuestion 57
Block A rests on inclined surface of wedge B which rests on a horizontal surface. The block A is connected to a string, which passes over a pulley P (fixed rigidly to the wedge B) and its other end is securely fixed to a wall at Q. Segment PQ of the string is horizontal and Q is at a large distance from P. The system is let go from rest and the wedge slides to right as A moves on its inclined face. Find the distance travelled by A by the time it reaches the bottom of the inclined surface.
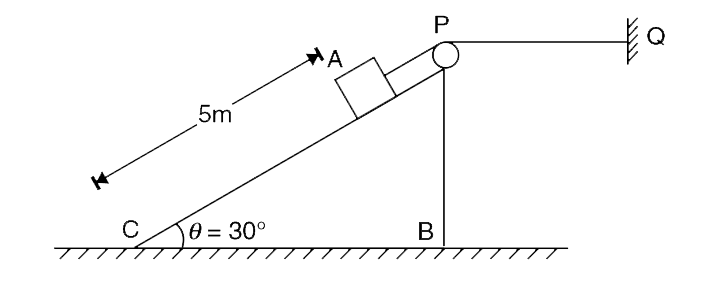 View Solution
View Solution