Five particles are projected simultaneously from the top of a tower that is h=32m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal.
![Five particles are projected simultaneously from the top of a tower that is h = 32 m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal. (a) Which particle will hit the ground first? (b) Separation between which two particles is maximum at the instant the first particle hits the ground? (c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground. [g = 10 m//s^(2), tan 37^(@) = (3)/(4)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C02_E01_096_Q01.png)
(a) Which particle will hit the ground first?
(b) Separation between which two particles is maximum at the instant the first particle hits the ground?
(c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground.
[g=10m/s2,tan37∘=34]
The correct Answer is:(a) particle 1 (b) particle 2 and 5 (c) particle 3 and 4;50.94m
Step by step video, text & image solution for Five particles are projected simultaneously from the top of a tower that is h = 32 m high. The initial velocities of projection are as shown in figure. Velocity of 2 and 5 are horizontal. (a) Which particle will hit the ground first? (b) Separation between which two particles is maximum at the instant the first particle hits the ground? (c) Which two particles are last and last but one to hit the ground? Calculate the distance between these two particles (still in air), at a time 0.3s after the third particle lands on ground. [g = 10 m//s^(2), tan 37^(@) = (3)/(4)] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 3
33 Videos
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 3
33 Videos
- HEAT TRANSFERBOOK - ARIHANTCHAPTER - HEAT TRANSFEREXERCISE - Heat Transfer
45 Videos
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
Similar Questions
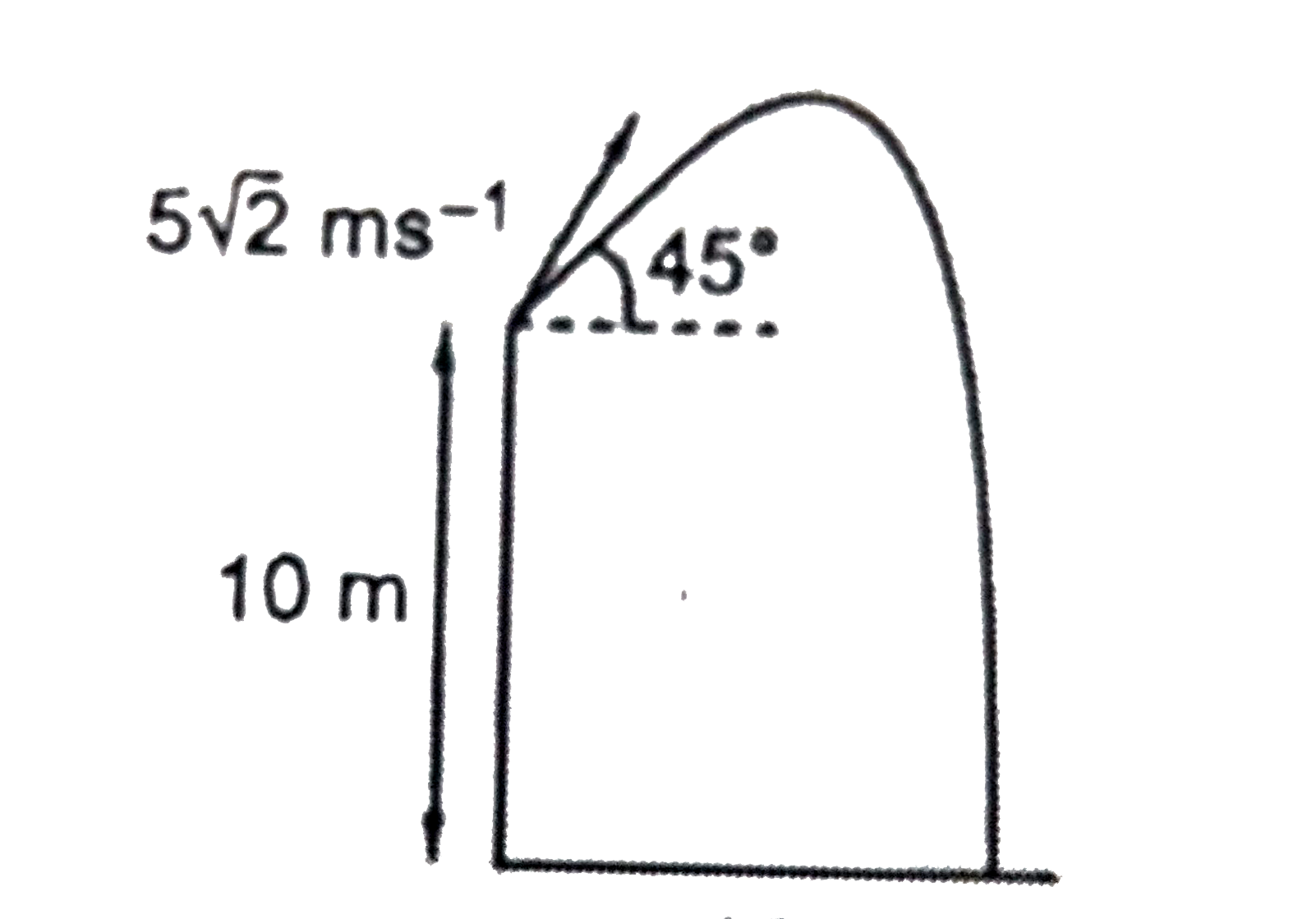
Particle projected from tower fo heigh 10m as shown in figure. Find the time (in sec) after which particle will hit the ground.
View SolutionA particle is projected from the top of a tower of height H. Initial velocity of projection is u at an angle θ above the horizontal . Particle hits the ground at a distance R from the bottom of tower. What should be the angle of projection θ so that R is maximum ? What is the maximum value of R?
View Solution
Knowledge Check
Two particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
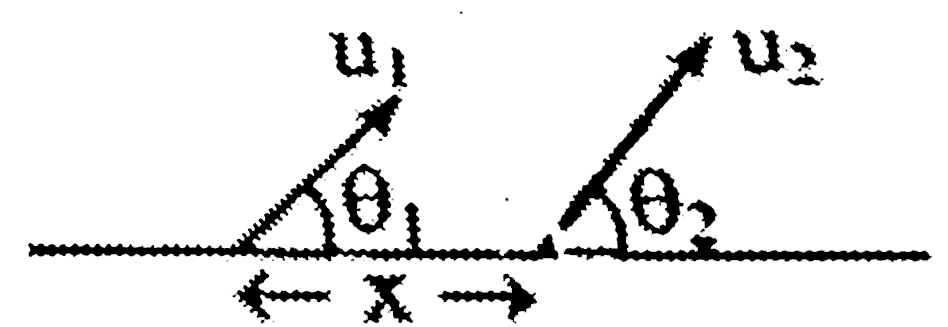Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)Two particles are projected simultaneously from the top of the towers as shown. Find the distance between the towers if they collide in mid air during their flight.
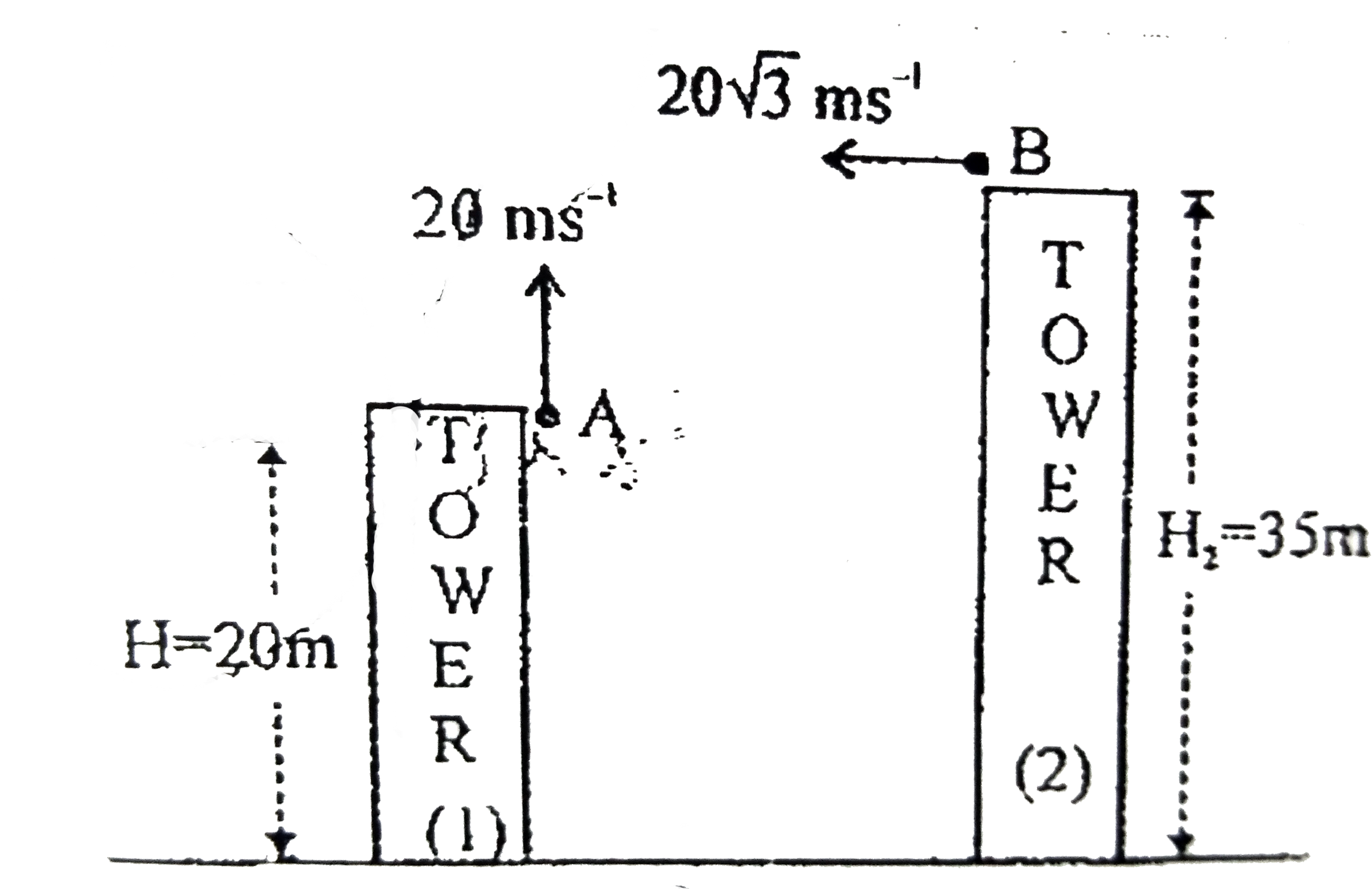A15mB20mC15√3mD5√3mParticle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
AT2g2BT2g4CT2g8DT2g5
Paragraph- Two particles are projected simultaneously from the top of a tower of height 80m horizontally in mutually perpendicular directions at equal speed of 40m/s. Q.The relative velocity of particles when they strike the ground is: m/s
View SolutionA particle is projected from point O on level ground towards a smooth vertical wall 50m from O and hits the wall. The initial velocity of the particle is 30m/s at 45° to the horizontal and the coefficient of restitution between the particle and the wall is e. Find the distance from O of the point at which the particle hits the ground again if
e = 0
View SolutionA particle is projected from point O on level ground towards a smooth vertical wall 50m from O and hits the wall. The initial velocity of the particle is 30m/s at 45° to the horizontal and the coefficient of restitution between the particle and the wall is e. Find the distance from O of the point at which the particle hits the ground again if
e = 1
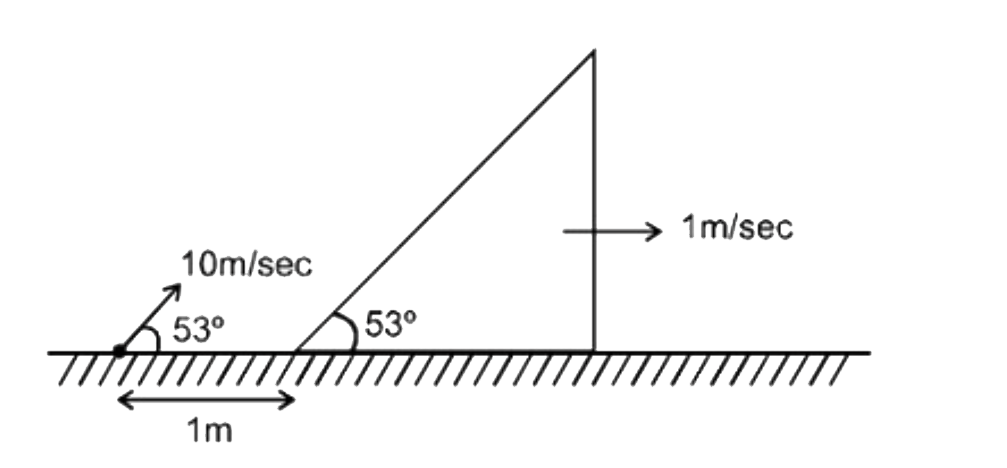
View SolutionA particle is projected from the ground and simultaneously a wedge starts moving towards the right, as shown in the figure. The maximum height of the wedge for which the particle will not hit the wedge is [g=10ms−2]
View SolutionTwo particles are projected simultaneously from two points O and O' such that 10m is the horizontal and 5m is the vertical distance between them as shown in the figure. They are projected at the same inclination 60∘ to the horizontal with the same velocit 10ms−1. The time after which their separation becomes minimum is
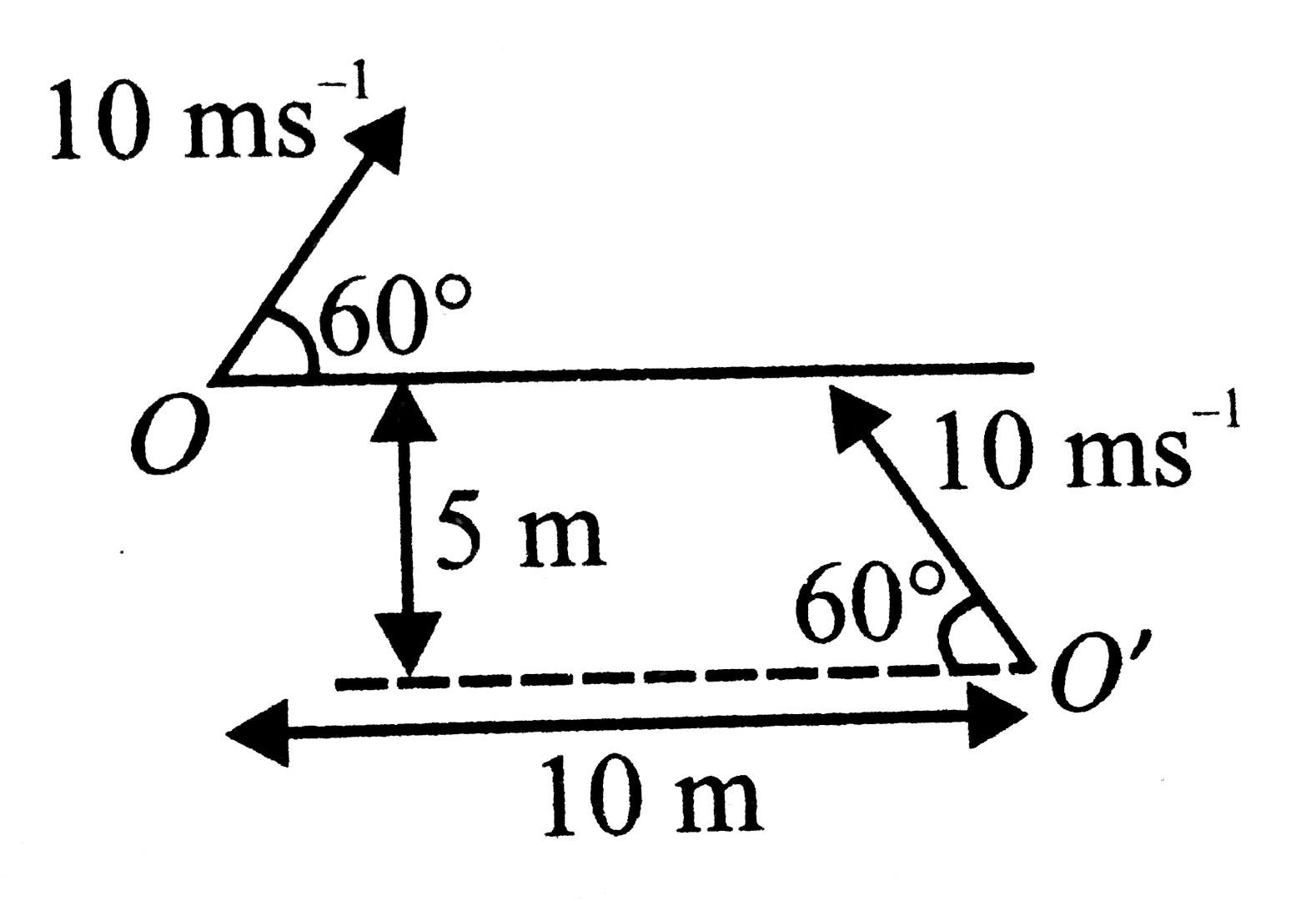
View Solution