Exercises from BHARATI BHAWAN PHYSICS Chapter 20 ROTATIONAL DYNAMICS, MOMENT OF INERTIA for Class 11
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL DYNAMICS, MOMENT OF INERTIA |
| BHARATI BHAWAN PHYSICS | Exercises |
| Medium | English |
| Academic Year | 2023-2024 |
Question 8
A flywheel of mass 5 kg and radius 10 cm rolls down a plane inclined at 30∘ to the horizontal. It rolls from rest through 100 cm in 10s. Neglecting friction find a) the kinetic energy of the flywheel at the end of 10s, (b) the momentum of intertia of the flywheel about its axis. View SolutionQuestion 13
A student sits on a stool that is free to rotate about a vertical axis. He holds out his arms horizontally, with a 4-kg weight in each hand. The stool is set in rotation with angular speed of 0.5 revolution per second. Calcualate the angular speed of the student is 90 cm and his rotational inertia is 7kg m2.
[Hint: Use conservation principle]View SolutionQuestion 14
A solid sphere of 1kg reaches the bottom of an inclined plane after rolling without slipping over a horizontal plane with velocity of 20ms−1. The inclination of the plane with the horizontal is 30∘. What is the velocity of the center of mass of the sphere immediately after it starts moving up the plane? Up to what distance along the plane will it rise? Assume sufficient friction to prevent slipping. View SolutionQuestion 18
A string is wrapped around a cylinder of mass M and radius r. The string is pulled vertically upward to prevent the center of mass from falling as the cylinder unwinds the string. (a) What is the tension in the string? B) How much work has been done on the cylinder once it has reached an angular speed ω? c) what is the length of string unwound in the time its acquires angular speed ω?View SolutionQuestion 19
A small sphere of mass m and radius r rolls without slipping on the insides of a large hemisphere of radius R whose axis of symmetry is vertical. Its starts at the top from rest. What is the kinetic energy of the small sphere at the bottom? What fraction is rotational and what transiational? What normal force does the small spheres exert on the hemisphere at the bottom?
[Hint: consider circular motion of center of mass at the bottom to calcualte normal reaction. For others consider conservation of energy.?View SolutionQuestion 21
a) Explain why the cushion of a billard table is made to receive the impact of the billard ball at height of 0.7 d where d is the diameter of the ball.
b) With what part of a sabre should an object be slashed in order that the user does not feel the impact on the hand? Consider the sabre as a uniform lamina.
[Hint: In either case if the striking point is at such a distance that the lower point remains at rest, there will a rise no force. Such a point is called center of impact].View SolutionQuestion 22
A right circular cylinder of radius r and mass m is suspended by a cord that is wound around its surface. It is allowed to fall, prove that at its center of gravity will follow a vertical rectilinear path and find the accleration along this path. Determine also the tensile force in the cord. View SolutionQuestion 23
The mass of the earth is increasing at the rate 1 part in 5×2019 per day by the accretion of meteors falling normally upon the earth's surface. Find the corresponding rate of change of the period of rotation of the earth supporting the earth to be a sphere of uniform density.
[Hint: Consider the deposit as a spherical shell and apply principle of conservation of angular momentum]View SolutionQuestion 24
A meter stick of length l and mass M lies on a frictionlesss table. The stick is free to move in any way on the table. A hockey ball of mass m moving perpendicuarly to the mass of the ball so that it remains at rest immediately after the collision?
[Hint: Elastic collision means that kinetic energy is conserved in the process. Consider conservation of kinetic energy, conservation of angualr momentum and linear momentum, i.e., 12mv2 = (12Mv2'+12Iε2, mv12=Iε, mv=Mv′.
Eliminate v2' and w2 from the first with the help of the other two. Use the expression I=112MI2]View SolutionQuestion 25
A long light thread is wond partly around cylinder of radius r and mass m partly on a simialr cylinder but free to turn about a fixed axis. The movable one is allowed to fall from rest. Find the velocity of the cylinder as a functiono of the height h through which it has fallen. Does the cylinder fall without slipping? View SolutionQuestion 27
Show that in order to get a billiard ball to roll without sliding from the start the cue must hit the ball not at the center (that is, a height above the table equal to the ball's radius R) but exactly at a height 25R above the center
[Hint, Consider linear momentum and angular motion of the ball. Apply the condtion for rolling without sliding. F = ma and τ=F×h=25mR2×α. Condition rolling without a sliding it a=αR]View SolutionQuestion 28
Two masses 500 g and 460g are suspended from the ends of a light string passing over a frictionless heavy pulley of radius 5cm. When released from rest the heavier mass is observed to fall 75cm in 5s. What is the rotational inertia of the pulley? ltbr> [Hint: When the pulley is heavy the tensions on the two slides are different.]View SolutionQuestion 29
A solid cylinder of weight 20 kg and radius 7.5 cm is placed on a inclined plane with inclination 30∘ to the horizontal. A light thin tape is wound around the cylinder and is taken tangentially over the upper surface parallel to the plane and finally attached to a 5-kg body after passing over a light smooth pulley. Find the tension in the tape and linear acceleration of the cylinder up the plance, assuming no slip.View SolutionQuestion 33
A uniform rod of length 2a is held at inclination α with the horizontla with its lower end at a height h above a horizontal plane surface and is let fall. It rebounds elastically from the plane. If you just before the other end touches the plane the rod makes the same angle with the horizontal, find the value of h in terms of a and α. View SolutionQuestion 34
An experimentor stands on a stool capable of rotating about a vertical axis and holds a rotating wheel of moment of intertia I1 about its axis and angualr velocity ε1 with its axis coinciding with the vertical axis of the stool. The moment of inertia of the stool and the experiment about the vertical axis is I2. Calculate the change in kinetic energy of the system if the experiment rotates the wheel through
i) 180∘ and ii) 90∘View SolutionQuestion 35
A uniform cylinder of radius R, and mass M rotates freely about a stationary horizontal axix O. A thin cord of length l and mass m is wound on the cylinder in a single layer and its free end is falling vertically. Find the acceleration as a function of the length x of the hanging part of the cord. Assume the center of mass of the wound part of the cord to be the axis of the cylinder.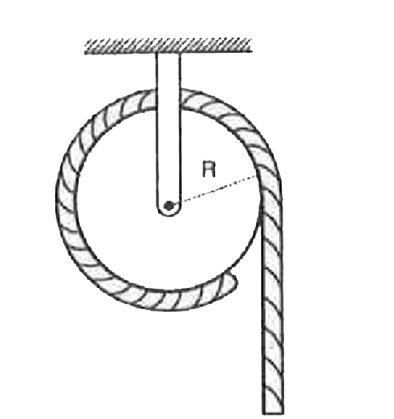
View SolutionQuestion 36
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.View SolutionQuestion 37
A man of mass m stands on the edge of a horizontal unifom disc of mass M and radius R whichis capable of rotating freely about a stationary vertical axis passing through its center. At a certain moment the man starts moving along the edge of the disc, he shifts over angle θ relative to the disc and then stops. Find the angle through which the disc rotates. View SolutionQuestion 38
A uniform solid cylinder of radius R=20cm rolls over a horizontal plane and passes on to an inclined plane meeting the horizontal plane at angle α=30∘ with the horizontal. Find the maximum value of velocity v0 which still permits the cylinder to roll into the inclined plane without a jump. Assume sliding to be absent. View SolutionQuestion 40
Two cylinders with radii r1 and r2 and rotational inertia I1 and I2 are supported on their horizontal axles. The first one is set in rotation with angular velocity ε. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them.
[Hint: Consider angular impulse received by the cylinders]View SolutionQuestion 42
A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v0(figure). At what values of v0 will the hoop move without bouncing?
View Solution