Two cylinders with radii r1 and r2 and rotational inertia I1 and I2 are supported on their horizontal axles. The first one is set in rotation with angular velocity ε. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them.
[Hint: Consider angular impulse received by the cylinders]
The correct Answer is:ω1=I1r22ωI1r22+I2r21 ω2=I1r1r2ωI1r21+I2r22
Step by step video, text & image solution for Two cylinders with radii r_(1) and r_(2) and rotational inertia I_(1) and I_(2) are supported on their horizontal axles. The first one is set in rotation with angular velocity epsilon. The axle of the other cylinder (smaller) is moved until it touches the large cylinder and is caused to rotate by the frictional forces between the two. Find the angualr velocity of the two cylinders after slipping ceases between them. [Hint: Consider angular impulse received by the cylinders] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABOOK - NN GHOSHCHAPTER - ROTATIONAL DYNAMICS, MOMENT OF INERTIAEXERCISE - Exercises
42 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
- SATURATED AND UNSATURATED VAPOURBOOK - NN GHOSHCHAPTER - SATURATED AND UNSATURATED VAPOUREXERCISE - All Questions
1 Videos
Similar Questions
Two cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
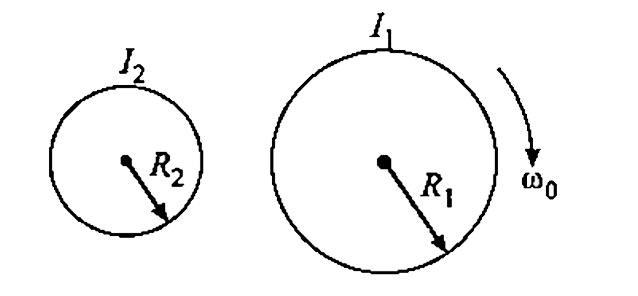
View SolutionFigure shows two cylinders of raddi r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slipover each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the sylinders after the slipping ceases.

View Solution
Knowledge Check
Two cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
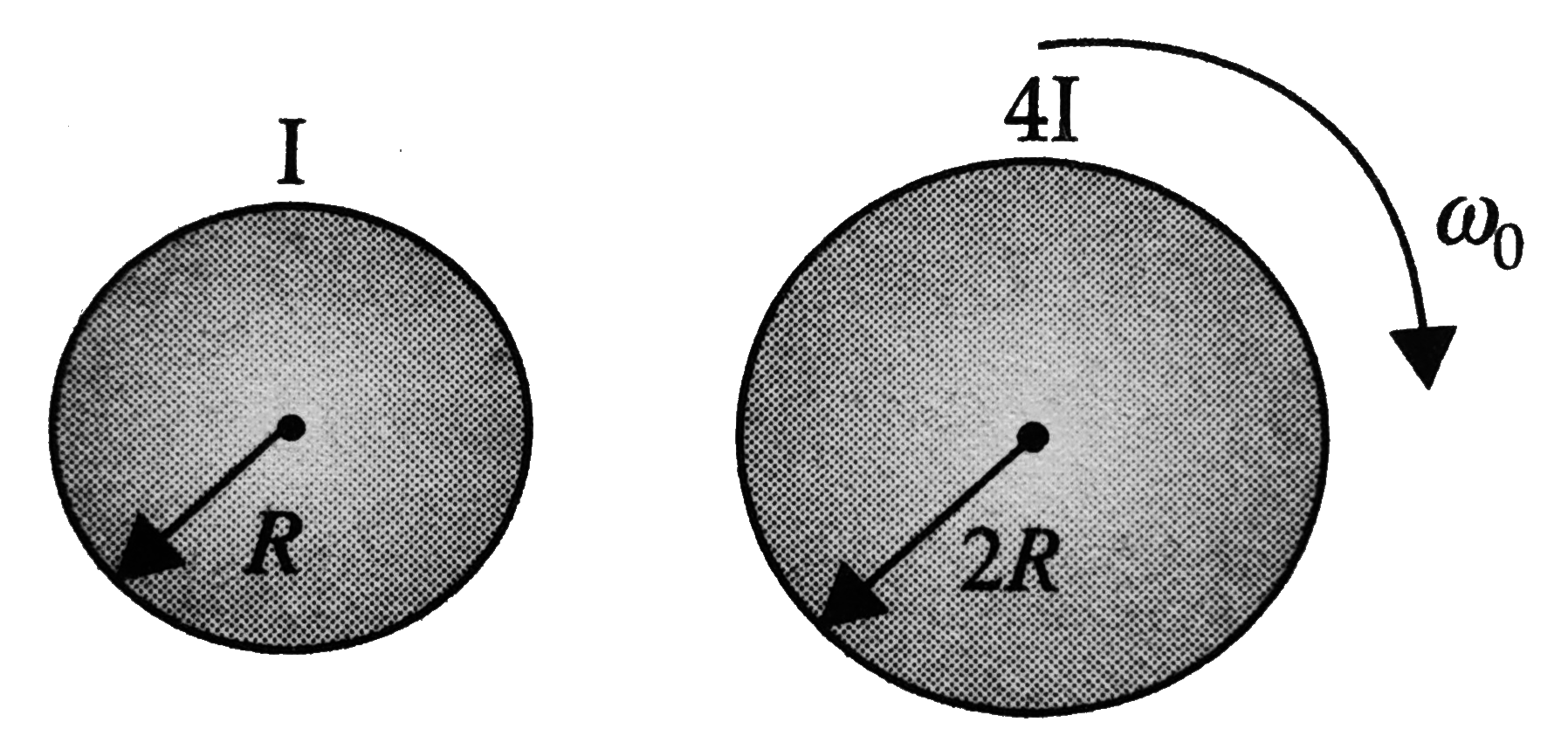 Aangular momentum of system is conservedBkinetic energy is conservedCneither the angular momentum nor the kinetic energy is conservedDboth the angular momentum and kinetic energy are conserved
Aangular momentum of system is conservedBkinetic energy is conservedCneither the angular momentum nor the kinetic energy is conservedDboth the angular momentum and kinetic energy are conservedThe heights of two cylinders are in the ratio of 3:1 . If the volumes of two cylinders be same , the ratio of their respective radii are :
A√3:1B1:√3C1:9Dnone of these
A solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA cylinder rests on a horizontal rotating disc, as shown in the figure. Find at what angular velocity, ω, the cylinder falls off the disc, if the distance between the axes of the disc and cylinder is R, and the coefficient of friction μ>D/h where D is the diameter of the cylinder and It is its height.

View SolutionA solid cylinder of mass 'M' and radius 'R' is rotating along its axis with angular velocity ω without friction. A particle of mass 'm' moving with velocity v collides aganist the cylinder and sticks to its rim. After the impact calculate angular velocity of cylinder .
View SolutionTwo horizontal discs A and B of radii r and 2r having moments of inertia I and 4I about their axes. Initially, disc A is rotating with ω0 and disc B is at rest. Their rims are now brought in contact. The discs first slip over each other at the contact but slipping finally ceases due to the fricition between them. Find the angular speeds of the discs after the slipping ceases. Also, find the loss in kinetic energy.
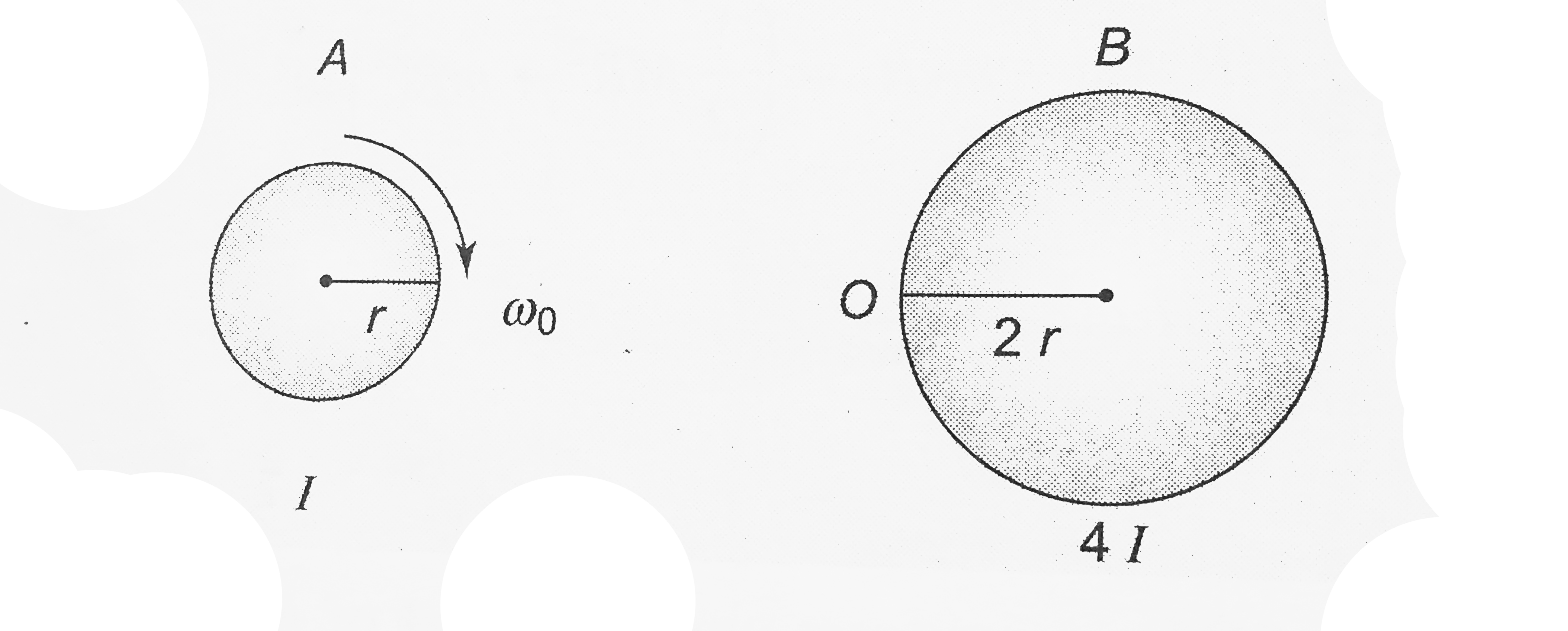
View SolutionThe ratio of height of two cylinders is 5:3, as well as the ratio of their radii is 2:3. find the ratio of the volumes of the cylinders.
View SolutionA cylinder of mass M, radius r1 and lenglth l is kept inside another cylinder of radius r2 and length l. The space between them is filled with a liquid of viscosity η. The inner cylinder starts rotating with angular velocity ω while the other cylinder is at rest. Find time when inner cylinder stops.
View Solution
