Exercise 18.4 from DC PANDEY ENGLISH SUPERPOSITION OF WAVES for Class 11
| Class 11 | PHYSICS |
| Chapter | SUPERPOSITION OF WAVES |
| DC PANDEY ENGLISH | Exercise 18.4 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
Three waves due to three coherent sources meet at one point. Their amplitudes are √2A0,3A0 and √2A0 . Intensity corresponding to A0 is l0. Phasse difference between first and second is 45∘. Path difference between first and third is λ4. In phase angle, first wave lags behind from the other two waves. Find resultant intensity at this point.View SolutionQuestion 5
A stationary wave is given by
y=5sin(πx)3cos40πt
where xandy are in cmandt is in second.
a. What are the amplitude and velocity of the component wave whose superposition can give rise to this vibration ?
b. What is the distance between the nodes ?
c. What is the velocity of a particle of the string at the position x=1.5cmwhent=9/8s?View SolutionQuestion 10
A wire is attached to a pan of mass 200 g that contains a 2.0 kg mass as shown in the figure. When plucked, the wire vibrates at a fundamental frequency of 220 Hz. An additional unknown mass M is then added to the pan and a fundamental frequency of 260 Hz is detected. What is the value of M?
 .View Solution
.View SolutionQuestion 14
The pulse shown in figure has a speed of 10cm/s .

(a) If the linear mass density of the right string is 0.25 that of the left string, at what speed does the transmitted pulse travel?
(b) Compare the heights of the transmitted pulse and the reflected pulse to that of the incident pulse. View SolutionQuestion 35
Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies ? (c) Which overtones are these frequencies ? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string ?View SolutionQuestion 39
Two wires of different densities are soldered together end to end then stretched under tension T. The waves speed in the first wire is twice that in the second wire.
(a) If the amplitude of incident wave is A, what are amplitudes of reflected and transmitted waves?
(b) Assuming no energy loss in the wire, find the fraction of the incident power that is reflected at the junction and fraction of the same that is transmitted. View SolutionQuestion 42
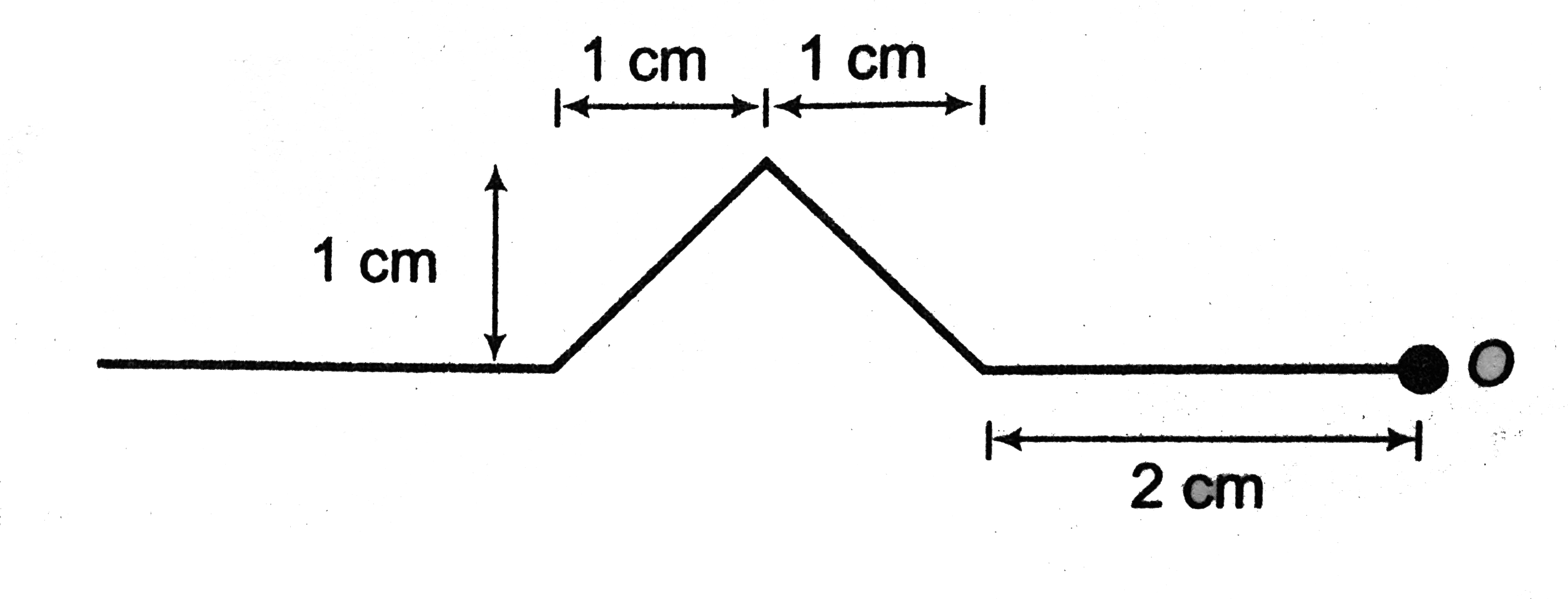
A string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N.A wave pulse is produced at t=0 nearj an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? (∈×10−2s)
 View Solution
View SolutionQuestion 44
Two sinusoidal waves combining in a medium are described by the equations
y1=(3.0cm)sinπ(x+0.60t)
and y2=(3.0cm)sinπ(x−0.06t)
where, x is in centimetres and t is in seconds. Determine the maximum displacement of the medium at
(a)x=0.250 cm,
(b)x=0.500 cm and
(c) x=1.50 cm.
(d) Find the three smallest values of x corresponding to antinodes. View SolutionQuestion 45
A standing wave is formed by the interference of two travelling waves, each of which has an amplitude A=πcm , angular wave number k=(π/2) per centimetre.
(a) Calculate the distance between two successive antinodes.
(b) What is the amplitude of the standing wave at x=0.50cm from a node? View SolutionQuestion 54
Adjacent antinodes of a standing wave on a string are 15.0 cm apart. A particle at an antinode oscillates in simple harmonic motion with amplitude 0.850 cm and period 0.0750 s. The string lies along the +x-axis and is fixed at x=0.
(a) find the displacement of a point on the string as a function of position and time.
(b) Find the speed of propagation of a transverse wave in the string.
(c) Find the amplitude at a point 3.0 cm to the right of an antinode. View SolutionQuestion 56
A thin taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation y(x,t)=(5.60cm)sin[(0.0340radcm)x]sin[(50.0rads)t], where the origin is at the left end of the string, the x-axis is along the string and the y-axis is perpendicular to the string.
(a) Draw a sketch that shows the standing wave pattern.
(b)Find the amplitude of the two travelling waves that make up this standing wave.
(c) What is the length of the string?
(d) Find the wavelength, frequency, period and speed of the travelling wave.
(e) Find the maximum transverse speed of a point on the string.
(f) What would be the equation y(x,t) for this string if it were vibrating in its eighth harmonic? View SolutionQuestion 57
A wire with mass 40.0 g is stretched so that its ends are tied down at points 80.0 cm apart.The wire vibrates in its fundamental mode with frequency 60.0 Hz and with an amplitude at the antinodes of 0.300 cm.
(a) What is the speed of propagation of transverse wave in the wire?
Compute the tension in the wire.
(c) Find the maximum transverse velocity and acceleration of particles in the wire. View SolutionQuestion 59
Figure shows different standing wave patterns on a string of linear mass density 4.0×10−2kg/m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).
 View Solution
View SolutionQuestion 60
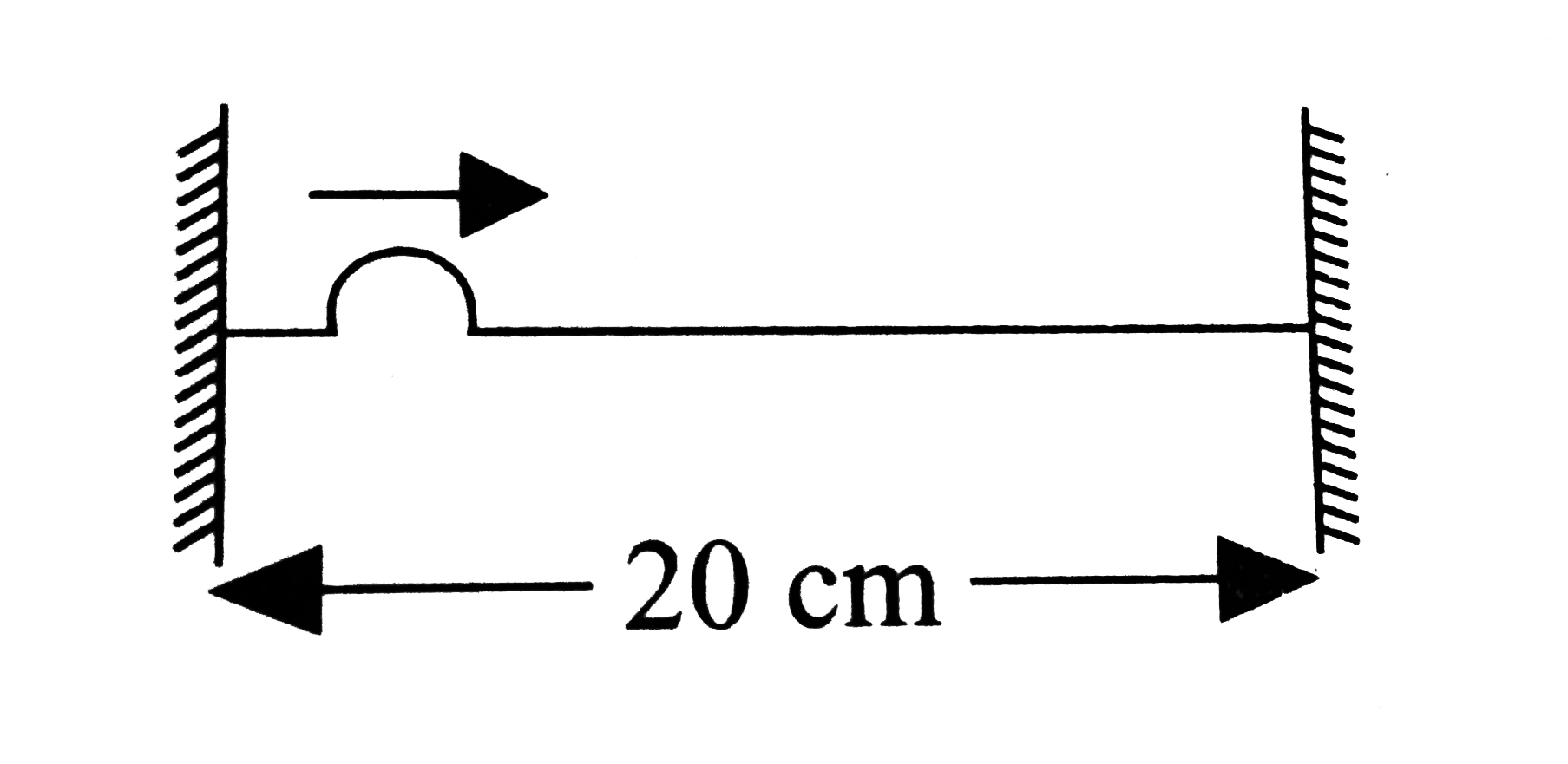
A 160 g rope 4 m long is fixed at one end and tied to a light string of the same length at the other end. Its tension is 400 N.
(a) What are the wavelength of the fundamental and the first two overtones?
(b) What are the frequencies of these standing waves?
[Hint : In this case, fixed end is a node and the end tied with the light string is antinode.]View SolutionQuestion 61
A string fastened at both ends has successive resonances with wavelengths of 0.54 m for nth harmonic and 0.48 m for the (n+1) th harmonic and 0.48 m for the (n+1) th harmonic.
(a) Which harmonics are these?
(b) What is the length of the stirng?
(c) What is the wavelength of the fundamental frequency? View SolutionQuestion 63
A string that is 10 cm long is fixed at both ends. At t=0, a pulse travelling from left to right at 1cm/sis4.0cm from the right end as shown in figure. Determine the next two times when the pulse will be at that point again. State in each case whether the pulse is upright or inverted .
 .View Solution
.View SolutionQuestion 70
A sting of length 1m and linear mass density 0.01 kg/m is stretched to a tension of 100 N. When both ends of the string are fixed, the three lowest frequencies for standing wave are f1,f2andf3 . When only one end of the string is fixed, the three lowest frequencies for standing wave are n1,n2andn3. Then, View SolutionQuestion 74
A man generates a symmetrical pulse in a string by moving his hand up and down. At t=0 the point in his hand moves downward. The pulse travels with speed of 3m/s on the string & his hands passes 6 times in each second from the mean position. Then the point on the string at a distance 3m will reach its upper extreme first time at time t=View SolutionQuestion 87
Incident wave y=Asin(ax+bt+π2) is reflected by an obstacle at x = 0 which reduces intensity of reflected wave by 36%. Due to superposition, the resulting wave consists of a standing wave and a travelling wave given by
y=−1.6sinaxsinbt+cAcos(bt+ax)
where A, a, b and c are positive constants.
1. Amplitude of reflected wave is View SolutionQuestion 88
Incident wave y=Asin(ax+bt+π2) is reflected by an obstacle at x = 0 which reduces intensity of reflected wave by 36%. Due to superposition, the resulting wave consists of a standing wave and a travelling wave given by
y=−1.6sinaxsinbt+cAcos(bt+ax)
where A, a, b and c are positive constants.
2. Value of c is View SolutionQuestion 89
Incident wave y=Asin(ax+bt+π2) is reflected by an obstacle at x = 0 which reduces intensity of reflected wave by 36%. Due to superposition, the resulting wave consists of a standing wave and a travelling wave given by
y=−1.6sinaxsinbt+cAcos(bt+ax)
where A, a, b and c are positive constants.
3. Position of second antinode is View SolutionQuestion 90
Three pieces of string, each of length L, are joined together end-to-end, to make a combined string of length 3L. The first piece of string has mass per unit length μ1, the second piece has mass per unit length μ2=4μ1 and the third piece has mass per unit length μ3=μ1/4 .
(a) If the combined string is under tension F, how much time does it take a transverse wave to travel the entire length 3L? Give your answer in terms of L,F and μ1 .
(b) Does your answer to part (a) depend on the order in which the three piece are joined together? Explain.View SolutionQuestion 94
A long wire PQR is made by joining two wires PQ and QR of equal radii. PQ has length 4.8m and mass 0.06kg. QR has length 2.56m and mass 0.2kg. The wire PQR is under a tension of 80N. A sinusoidal wave-pulse of amplitude 3.5cm is sent along the wire PQ from end P. No power is dissipated during the propagation of the wave-pulse. Calculate,
(a) the time taken by the wave-pulse to reach the other end R of the wire, and
(b) the amplitude of the reflected and transmitted wave-pulse after the incident wave-pulse crosses the joint Q. View SolutionQuestion 95
A light string is tied at one end to a fixed support and to a heavy string of equal length L at the other end as shown in figure. A block of mass m is tied to the free end of heavy string. Mass per unit length of the strings are μ and 9μ and the tension is T. Find the possible values of frequencies such that junction of two wire point A is a node.
 View Solution
View SolutionQuestion 96
A string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibratin ?View SolutionQuestion 98
Three component sinusoidal waves progressing in the same directions along the same path have the same period byt their amplitudes are A,A2andA3. The phases of the variation at any position x on their path at time t=0are0,−π2and−π respectively. Find the amplitude and phase of the resultant wave. View SolutionQuestion 99
A metal rod of length 1m is clamped at two points as shown in the figure. Distance of the clamp from the two ends are 5 cm and 15 cm, respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young's modulus of elasticity and density of aluminium are Y=1.6×1011Nm−2 and ρ=2500kgm−3 , respectively.
 View Solution
View SolutionQuestion 100
y1=8sin(ωt−kx)andy2=6sin(ωt+kx) are two waves travelling in a string of area of cross-section s and density rho. These two waves are superimposed to produce a standing wave.
(a) Find the energy of the standing wave between two consecutive nodes.
(b) Find the total amount of energy crossing through a node per second. View Solution
All Exercises from DC PANDEY ENGLISH Class 11 PHYSICS SUPERPOSITION OF WAVES
- EXERCISE 18.1
- EXERCISE 18.2
- EXERCISE 18.3
- EXERCISE 18.4
- LEVEL 1 ASSERTION AND REASON
- LEVEL 1 OBJECTIVE
- LEVEL 1 SUBJECTIVE
- LEVEL 2 COMPREHENSION BASED
- LEVEL 2 MORE THAN ONE CORRECT
- LEVEL 2 SINGLE CORRECT
- LEVEL 2 SUBJECTIVE
- MORE THAN ONE CORRECT OPTIONS
- OBJECTIVE QUESTIONS
- SUBJECTIVE QUESTIONS
- EXAMPLE
- EXAMPLE TYPE 1
- EXAMPLE TYPE 2
- EXAMPLE TYPE 3
- EXAMPLE TYPE 4
- MISCELLANEOUS EXAMPLE

 .
.