Level 2 Subjective from DC PANDEY PHYSICS Chapter 6 CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION for Class 11
| Class 11 | PHYSICS |
| Chapter | CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION |
| DC PANDEY PHYSICS | Level 2 Subjective |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
A ball of negligible size and mass m is given a velocity v0 on the centre of the cart which has a mass M and is originally at rest. If the coefficient of restitution between the ball and walls A and B is e. Determine the velocity of the ball and the cart just after the ball strikes A. Also, determine the total time needed for the ball to strike A, rebound, then strike B, and rebound and then return to the centre of the cart. Neglect friction.
 View Solution
View SolutionQuestion 3
Two point masses m1 and m2 are connected by a spring of natural length l0. The spring is compressed such that the two point masses touch each other and then they are fastened by a string. Then the system is moved with a velocity v0 along positive x-axis. When the system reached the origin, the string breaks (t=0). The position of the point mass m1 is given by x1=v0t−A(1−cosωt) where A and ω are constants. Find the position of the second block as a function of time. Also, find the relation between A and l0. View SolutionQuestion 4
A small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.
 View Solution
View SolutionQuestion 5
A chain of length l and mass m lies in a pile on the floor. If its end A is raised vertically at a constant speed v0, express in terms of the length y of chain which is off the floor at any given instant.
(a) The magnitude of the force P applied to end A.
(b) Energy lost during the lifting of the chain.
 View Solution
View SolutionQuestion 6
(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
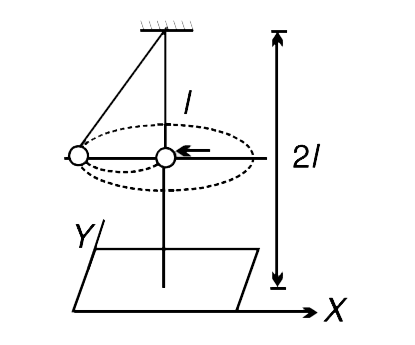
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ? View SolutionQuestion 7
A particle of mass 2m is projected at an angle of 45∘ with horizontal with a velocity of 20√2m/s. After 1s explosion takes place and the particle is broken into two equal pieces. As a result of explosion one part comes to rest. Find the maximum height attained by the other part. Take g=10m/s2.View SolutionQuestion 9
A gun of mass M(including the carriage) fires a shot of mass m. The gun along with the carriage is kept on a smooth horizontal surface. The muzzle speed of the bullet vr is constant. Find
(a) The elevation of the gun with horizontal at which maximum range of bullet with respect to the ground is obtained.
(b) The maximum range of the bullet.View SolutionQuestion 10
A ball is released from rest relative to the elevator at a distance h1 above the floor. The speed of the elevator at the time of ball release is v0. Determine the bounce height h2 relative to elevator of the ball (a) if v0 is constant and (b) if an upward elevator accleration a=g4 begins at the instant the ball is released. The coefficient of restitution for the impact is e.
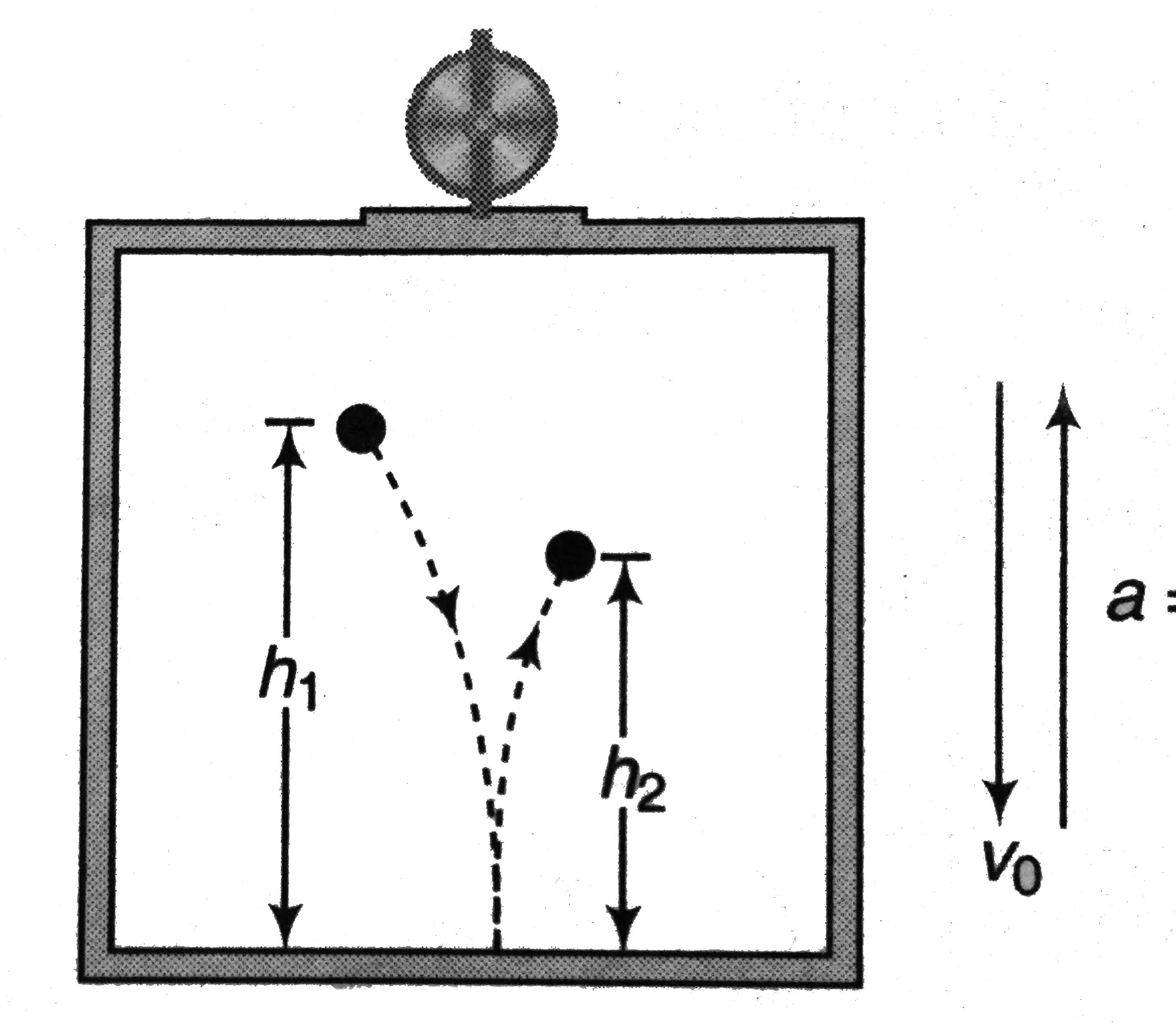 View Solution
View SolutionQuestion 11
A planck of mass 5kg is placed on a frictionless horizontal plane. Further a block of mass 1kg is placed over the plank. A massless spring of natural length 2m is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring's natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is 100N/m)
 View Solution
View SolutionQuestion 12
To test the manufactured properties of 10N steel balls, each ball is released from rest as shown and strikes a 45∘ inclined surface. If the coefficient of restitution is to be e=0.8, determine the distance s, where the ball must strike the horizontal plane at A. At what speed does the ball stike at A? (g=9.8m/s2)
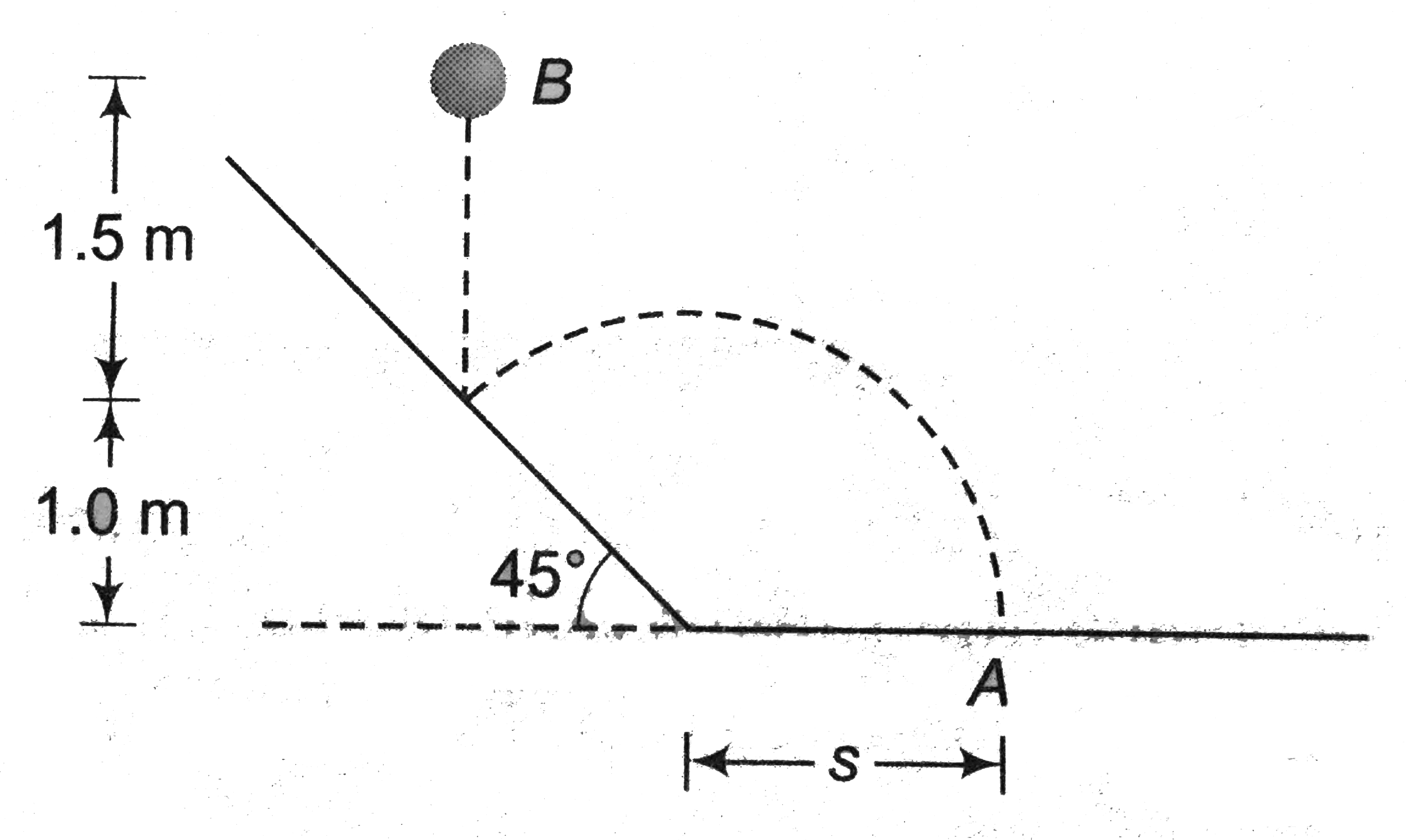 View Solution
View SolutionQuestion 14
A small cube of mass m slides down a circular path of radius R cut into a large block of mass M, as shown in figure. M rests on a table, and both blocks move without friction. The blocks are initially at rest, and m starts from the top of the path. Find the horizontal distance from the bottom of block where cube hits the cable
 View Solution
View SolutionQuestion 15
A thin hoop of mass M and radius r is placed on a horizontal plane. At the initial instant, the hoop is at rest. A small washer of mass m with zero initial velocity slides from the upper point of the hoop along a smooth groove in the inner surfaces of the hoop. Determine the velocity u of the centre of the hoop at the moment when the washer is at a certain point A of the hoop, whose radius vector forms an angle ϕ with the vertical (figure). The friction between the hoop and the plane should be neglected
 View Solution
View SolutionQuestion 16
A shell of mass 1kg is projected with velocity 20m/s at an angle 60∘ with horizontal. It collides inelastically with a ball of mass 1kg which is suspended through a thread of length 1m. The other end of the thread is attached to the ceiling of a trolley of mass 43kg as shown in figure. Initially the trolley is stationary and it is free to move along horizontal rails wihtout any friction. What is the maximum deflection of the thread with vertical? String does not slack. Take g=10m/s2.
 View Solution
View SolutionQuestion 17
A small ball is projected at an angle α between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.
 View Solution
View SolutionQuestion 18
Two large rigid vertical walls A and B are parallel to each other and separated by 10m. A particle of mass 10g is projected with an initial velocity of 20m/s at 45∘ to the horizontal from point P on the ground, such that AP=5m. The plane of motion of the particle is vertical and perpendicular to the walls. Assuming that all the collisions are perfectly elastic, find the maximum height attained by the particle and the total number of collisions suffered by the particle with the walls before it hits ground. Take g=10m/s2.
 View Solution
View SolutionQuestion 19
Two blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
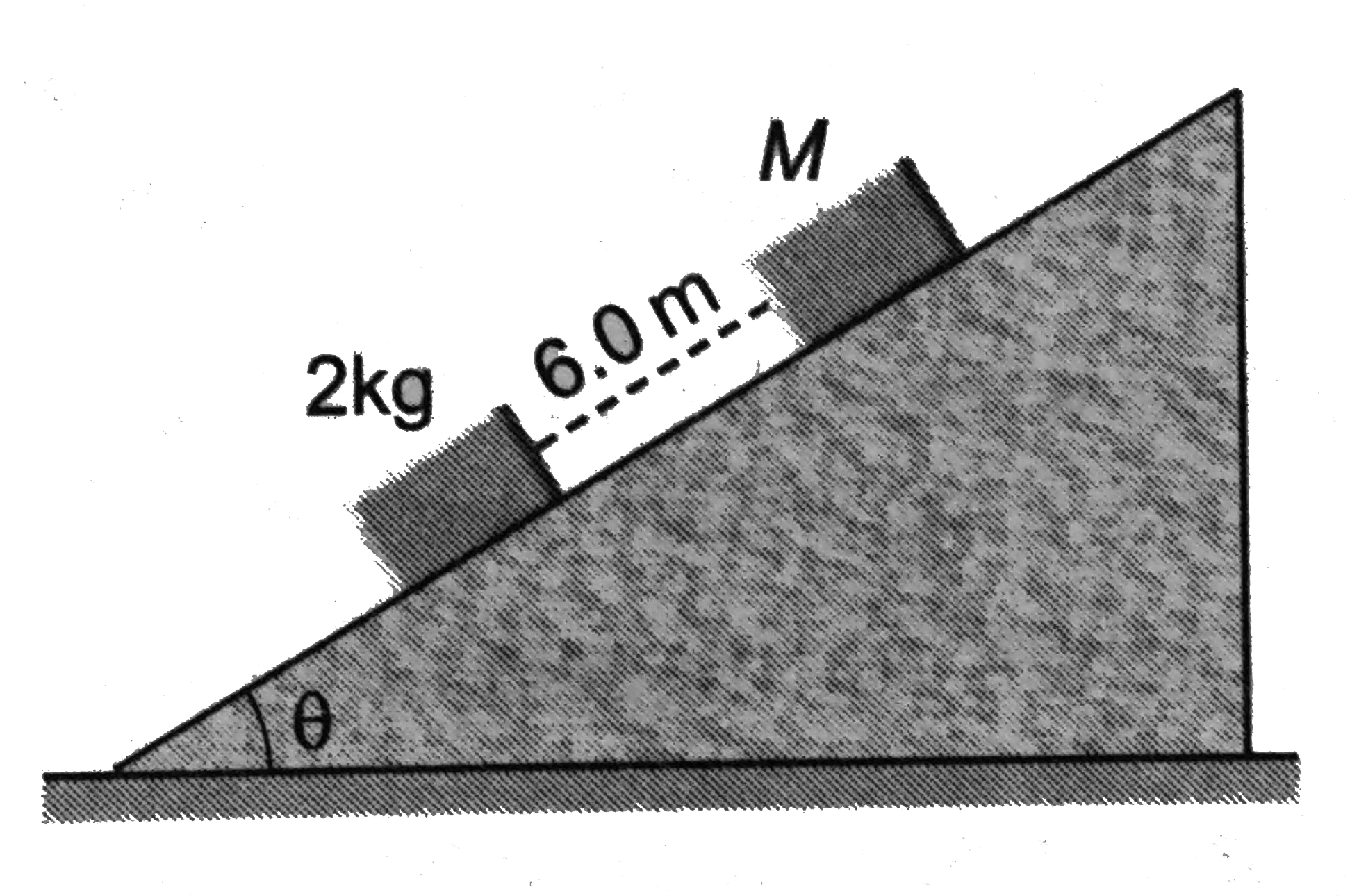 View Solution
View SolutionQuestion 20
A small block of mass m is placed on top of a smooth hemisphere also of mass m which is placed on a smooth horizontal surface. If the block begins to slide down due to a negligible small impulse, show that it will loose contact with the hemisphere when the radial line through vertical makes an angle θ given by the equaition cos3θ−6cosθ+4=0.
 View Solution
View Solution
All Exercises from DC PANDEY PHYSICS Class 11 PHYSICS CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- Example
- Exercise 11.1
- Exercise 11.2
- Exercise 11.3
- Exercise 11.4
- Exercise 11.5
- Exercise 11.6
- Level 1 Assertion and Reason
- Level 1 Objective
- Level 1 Subjective
- Level 1 Subjective Questions
- Level 2 Comprehension Based
- Level 2 Comprehension Based Questions
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Single Correct Option
- Level 2 Subjective
- MiscellaneousExamples
- Solved Examples
- Type 1
