A Only One Option is Correct from DC PANDEY PHYSICS Chapter 29 ROTATIONAL MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| DC PANDEY PHYSICS | A Only One Option is Correct |
| Medium | English |
| Academic Year | 2023-2024 |
Question 6
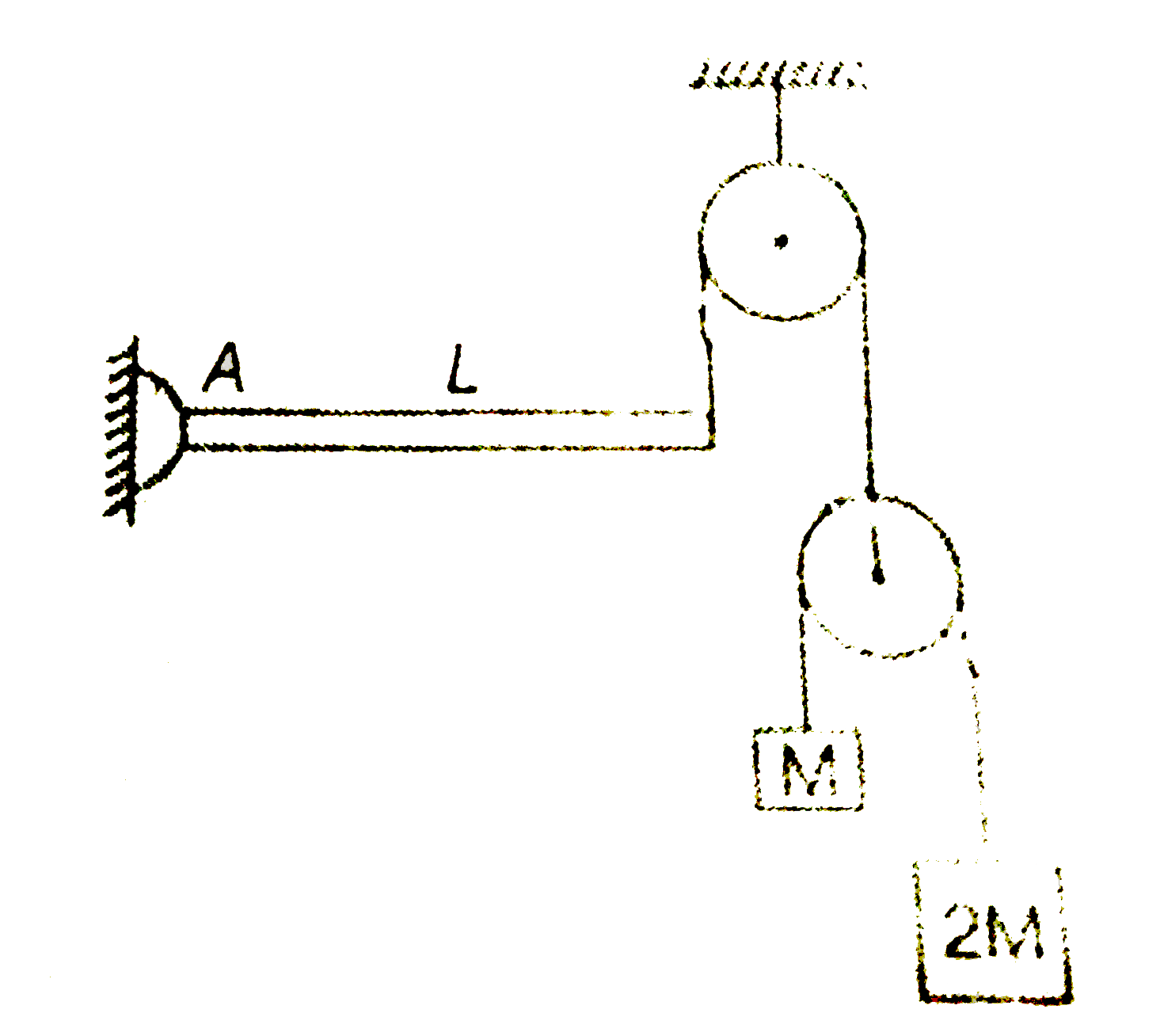
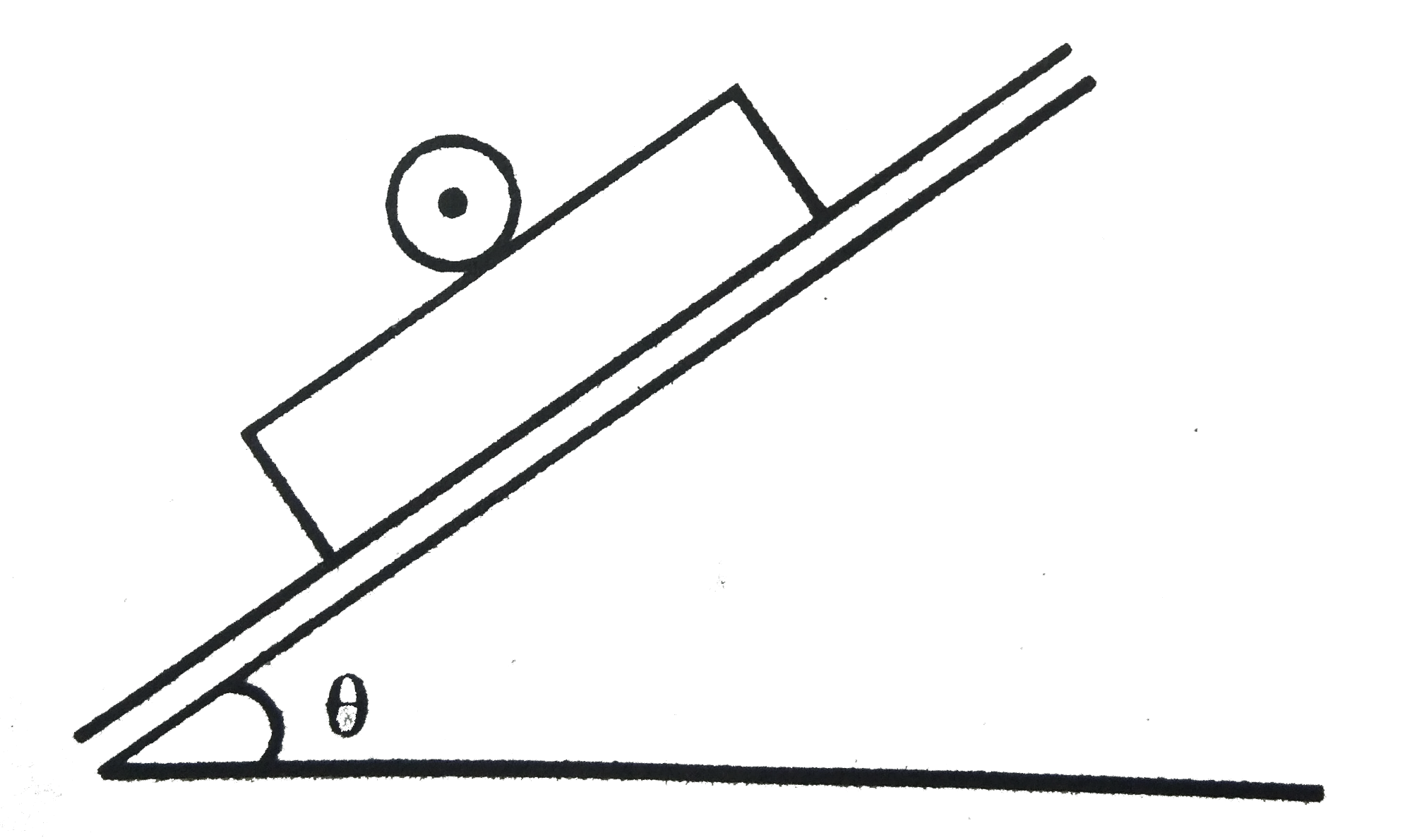
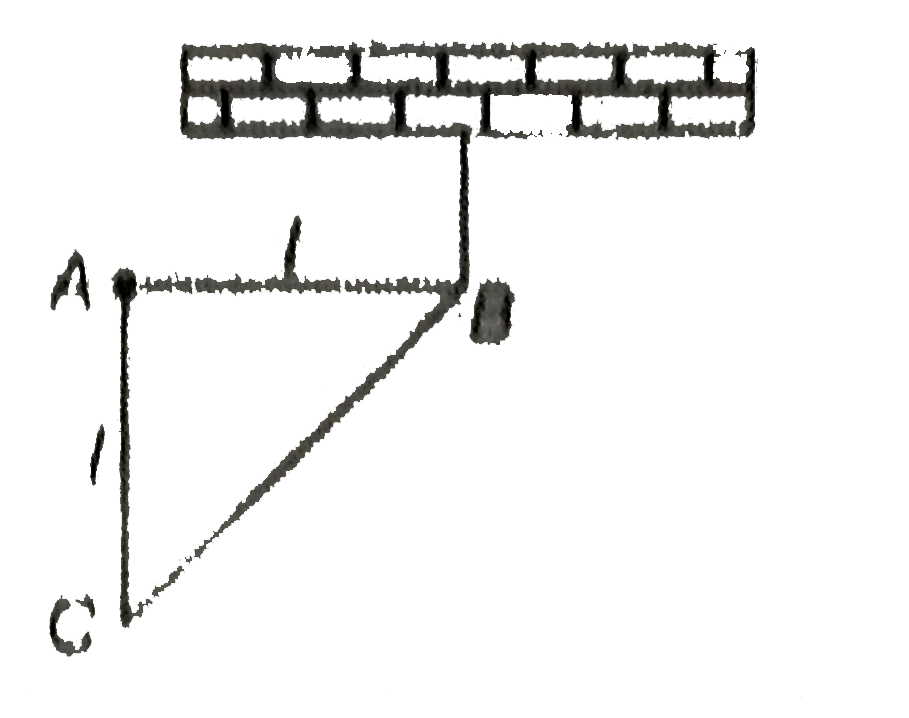
A uniform cylinder of mass M and radius R rolls without slipping down a slope of angle 8 with horizontal. The cylinder is connected to a spring of force constant k at the centre, the other side of which is connected to a fixed support at A. The cylinder is released when the spring is unstretched. The· force of friction (f):
 View Solution
View SolutionQuestion 8
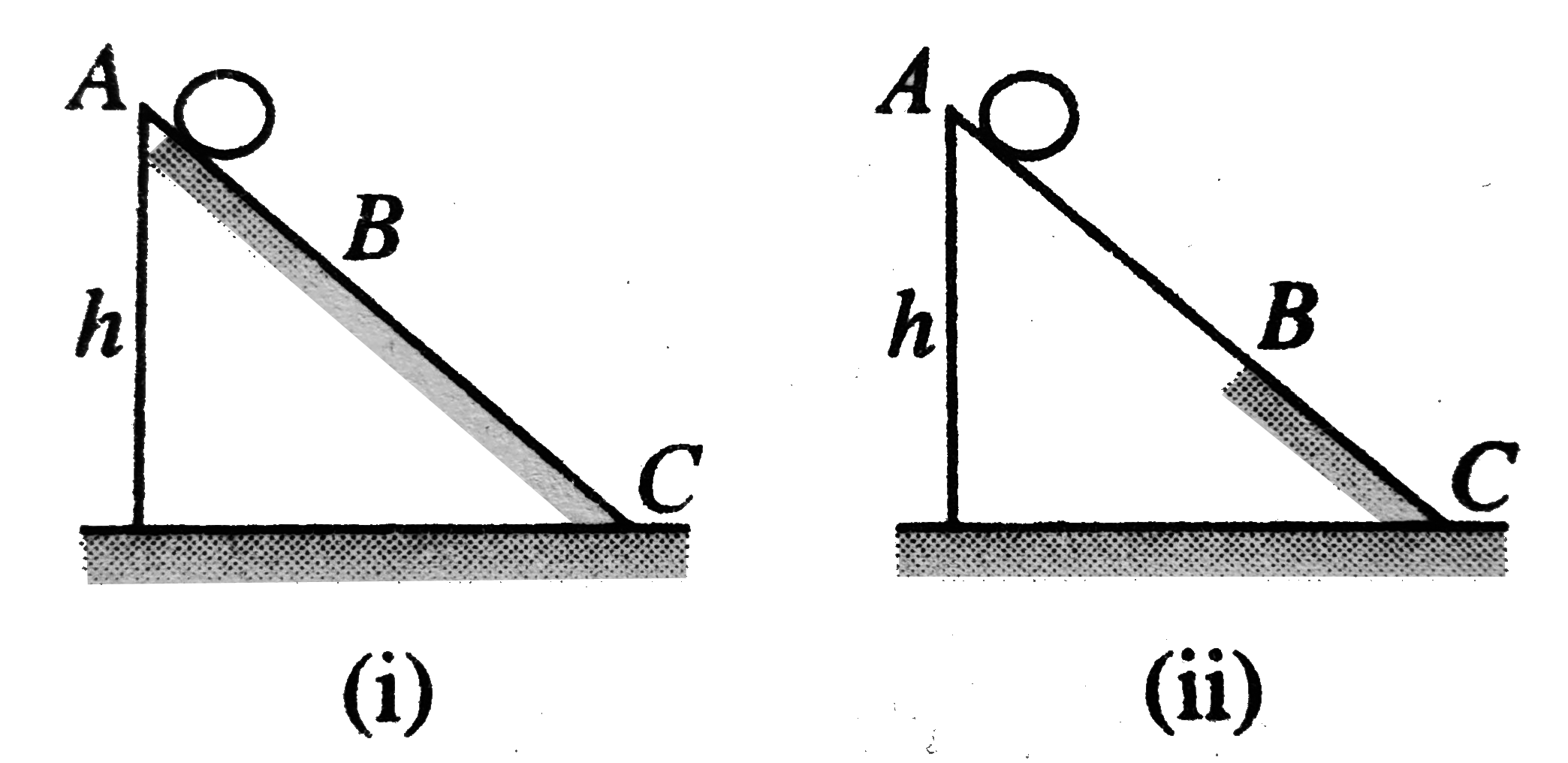
In both the figures all other factors are same, except that in figure (i) AB is rough and BC is smooth while in figure (ii) AB is smooth and BC is rough. In figure (i), if a sphere is released from rest it starts rolling. Now consider the figure (ii), if same sphere is A released from top of the inclined plane, what will be the kinetic energy of the sphere on reaching the bottom:
 View Solution
View SolutionQuestion 14
A uniform ring of mass m and radius R is released from top of an inclined plane. The plane makes an angle θ with horizontal. The cofficent of friction between the ring and plane is μ. Initially, the point of contact of ring and plane is P. Angular momentum of ring about an axis passing from point P and perpendicular to plane of motion as a function of time t isView SolutionQuestion 15
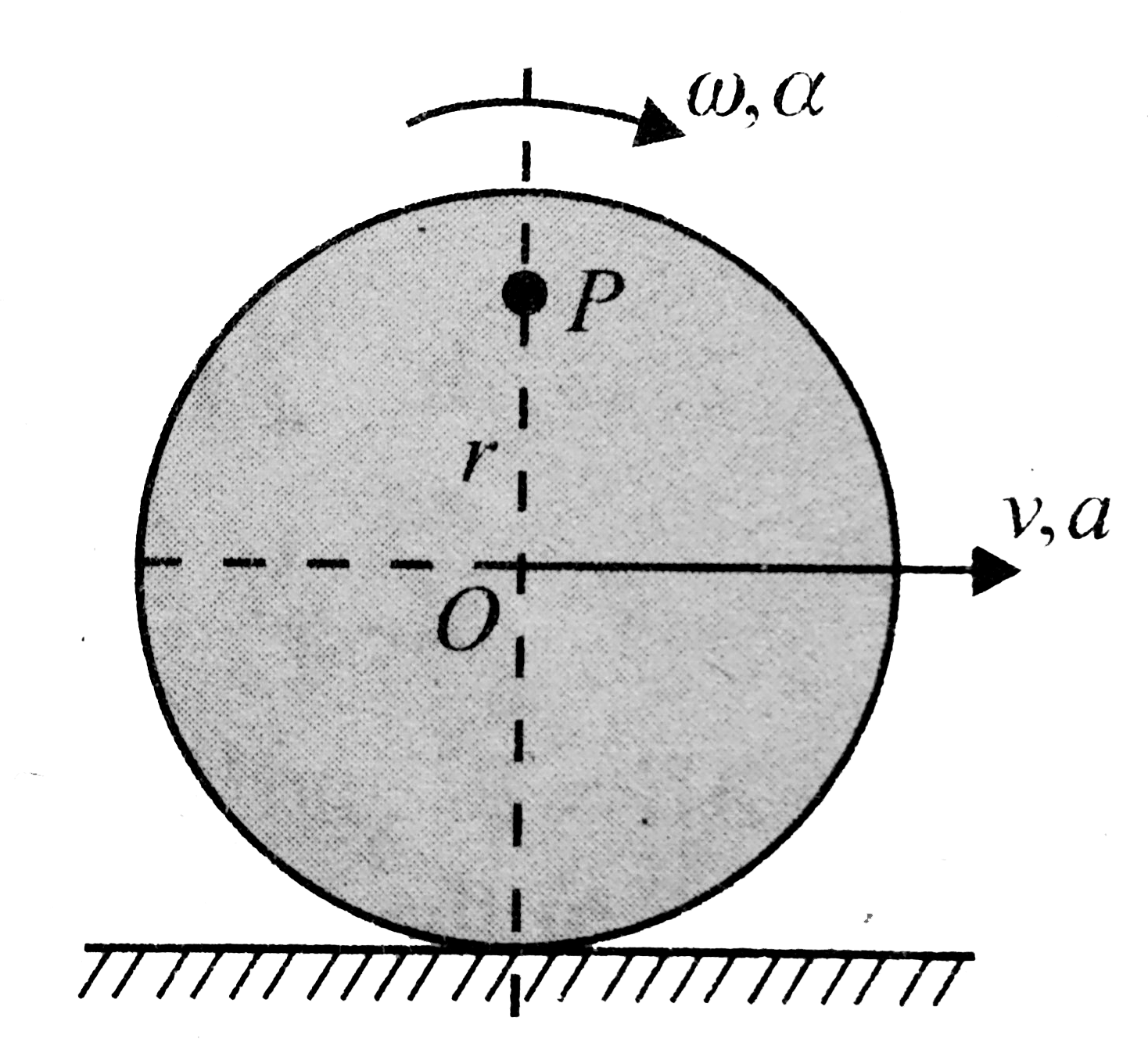
A wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)View SolutionQuestion 22
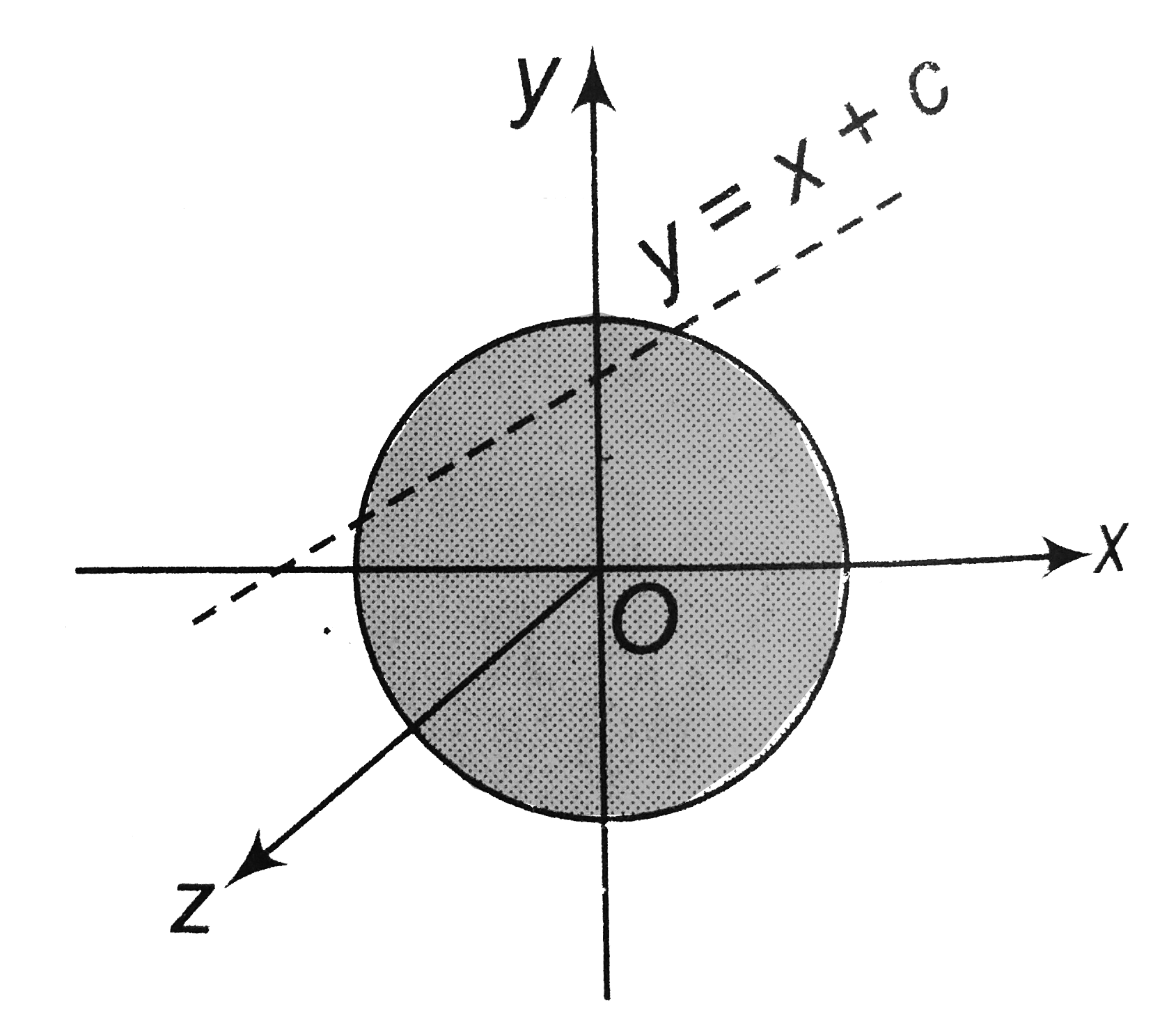
A wire of length l and mass m is first bent in a circle, then in a square and then in an equilateral triangle. The moment of inertia in these three cases about an axis perpendicular to their planes and passing through their centrer of mass are I1,I2 and I3 respectively. Then maximum of them is View SolutionQuestion 26
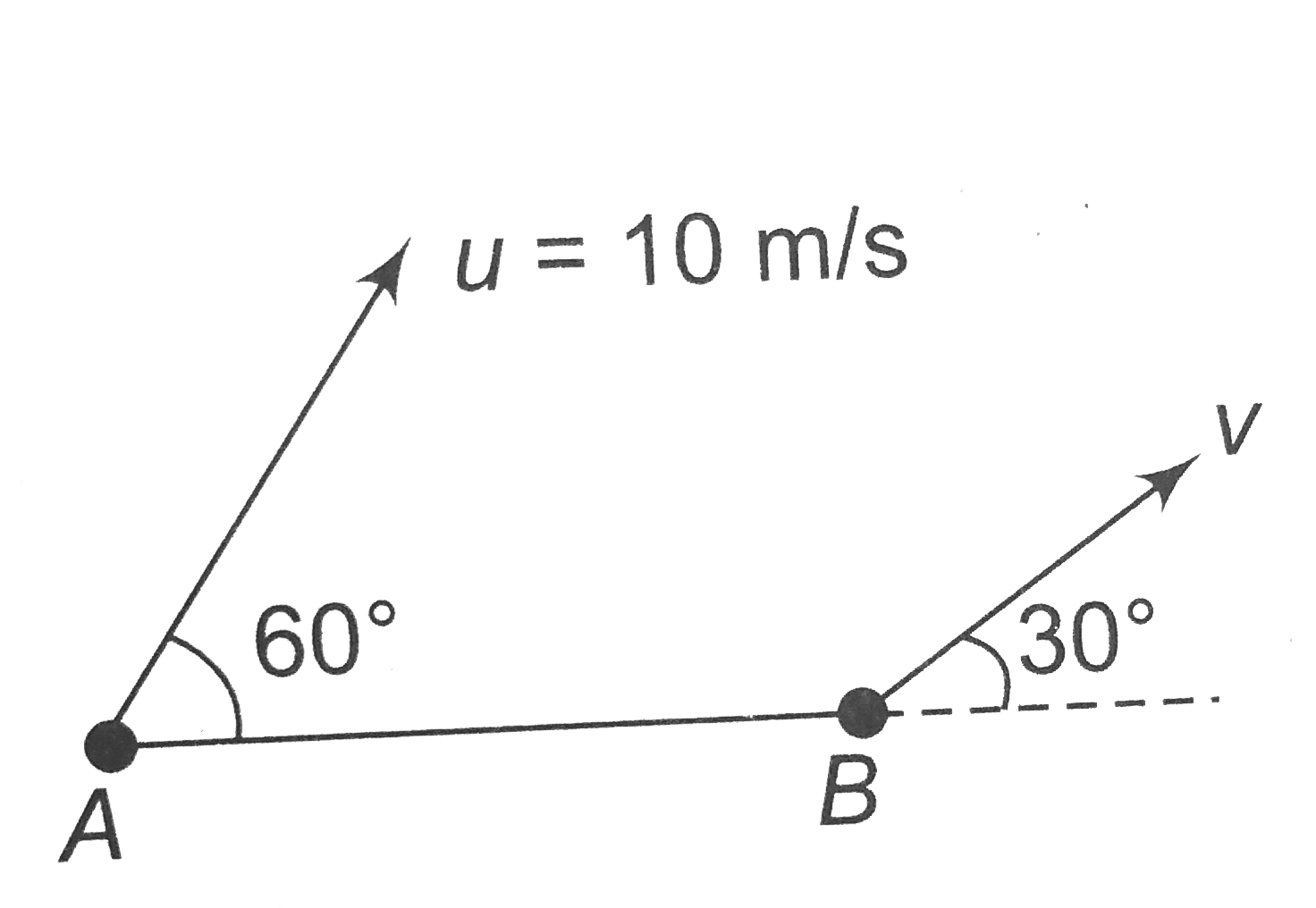
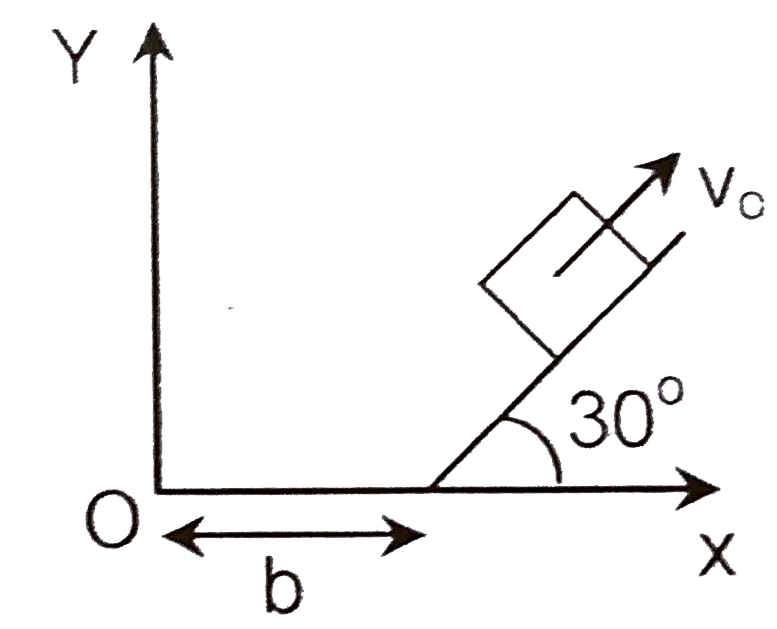
Two particles A and B are situated at a distance d=2m apart. Particle A has a velocity of 10m/s at an angle of 60∘ and particle B has a velocity v at an angle 30∘ as shown in figure. The distance d between A and B is constant. the angular velocity of B with respect to A is :
 .View Solution
.View SolutionQuestion 30
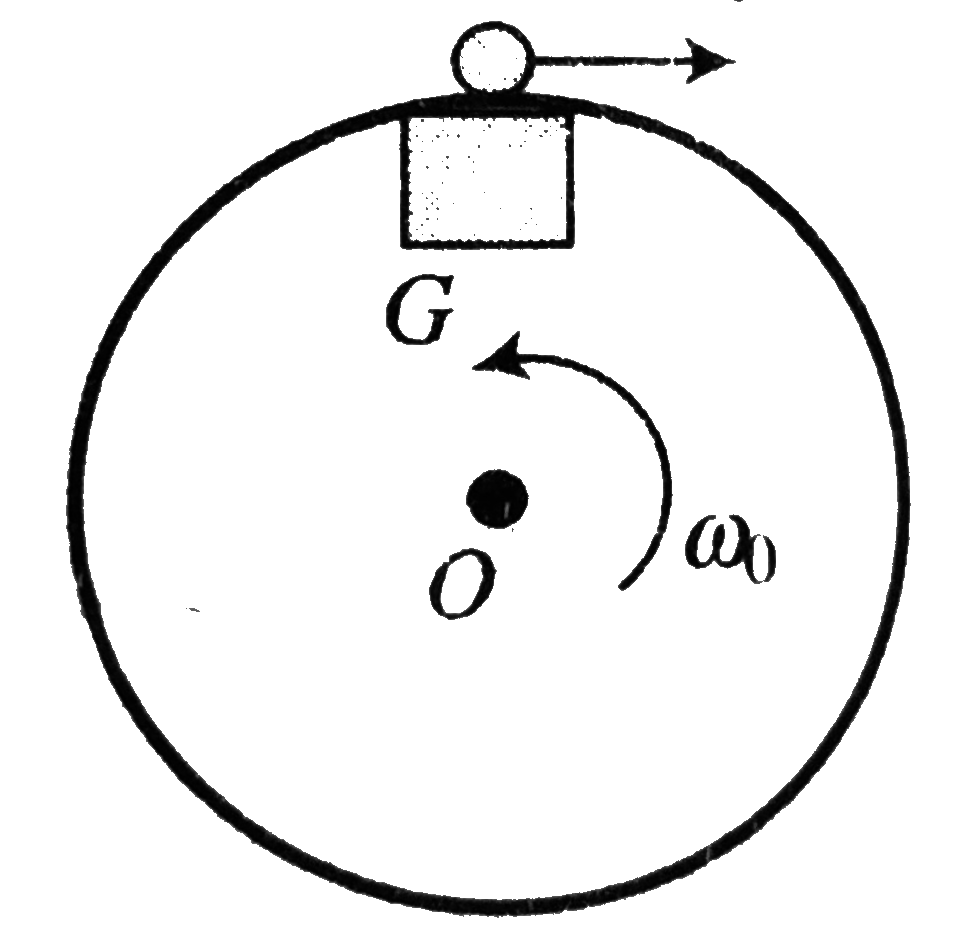
A horizontal turn table in the form of a disc of radius r carries a gun at G and rotates with angular velocity ω0 about a vertical axis passing through the centre O. The increase in angular velocity of the system if the gun fires a bullet of mass m with a tangential velocity v with respect to the gun is (moment of inertia of gun + table about O is I0
 View Solution
View SolutionQuestion 35
A spherical body of radius R is allowed to roll down on an incline with out slipping and it recheas with a speed v0 at the bottom. The incline is then made smooth by waxing and the body is allowed top slide without rolling and now the speed attained is 54v0 The radius of gyration of the body about an axis passing through the centre isView SolutionQuestion 42
In the figure shon mass of both, the spherical body and blocks is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no sliiping between any two surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
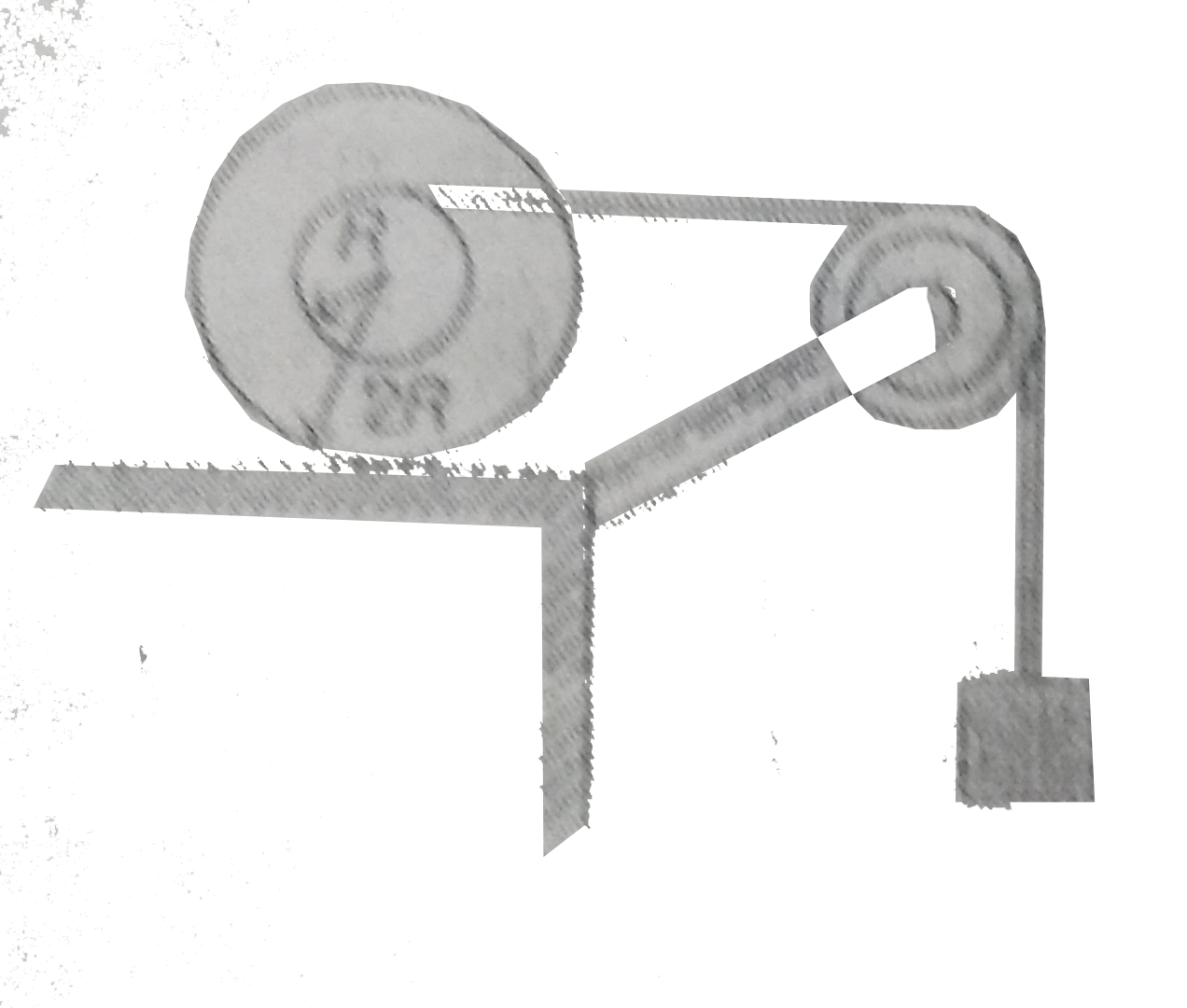 View Solution
View SolutionQuestion 47
A uniform rod AB of length L and mass M is lying on a smooth table. A small particle if mass m strike the rod with velocity v0 at point C at a distance comes to rest after collision. Then find the value of x, so that point A of the rod remains stationary just after collision.
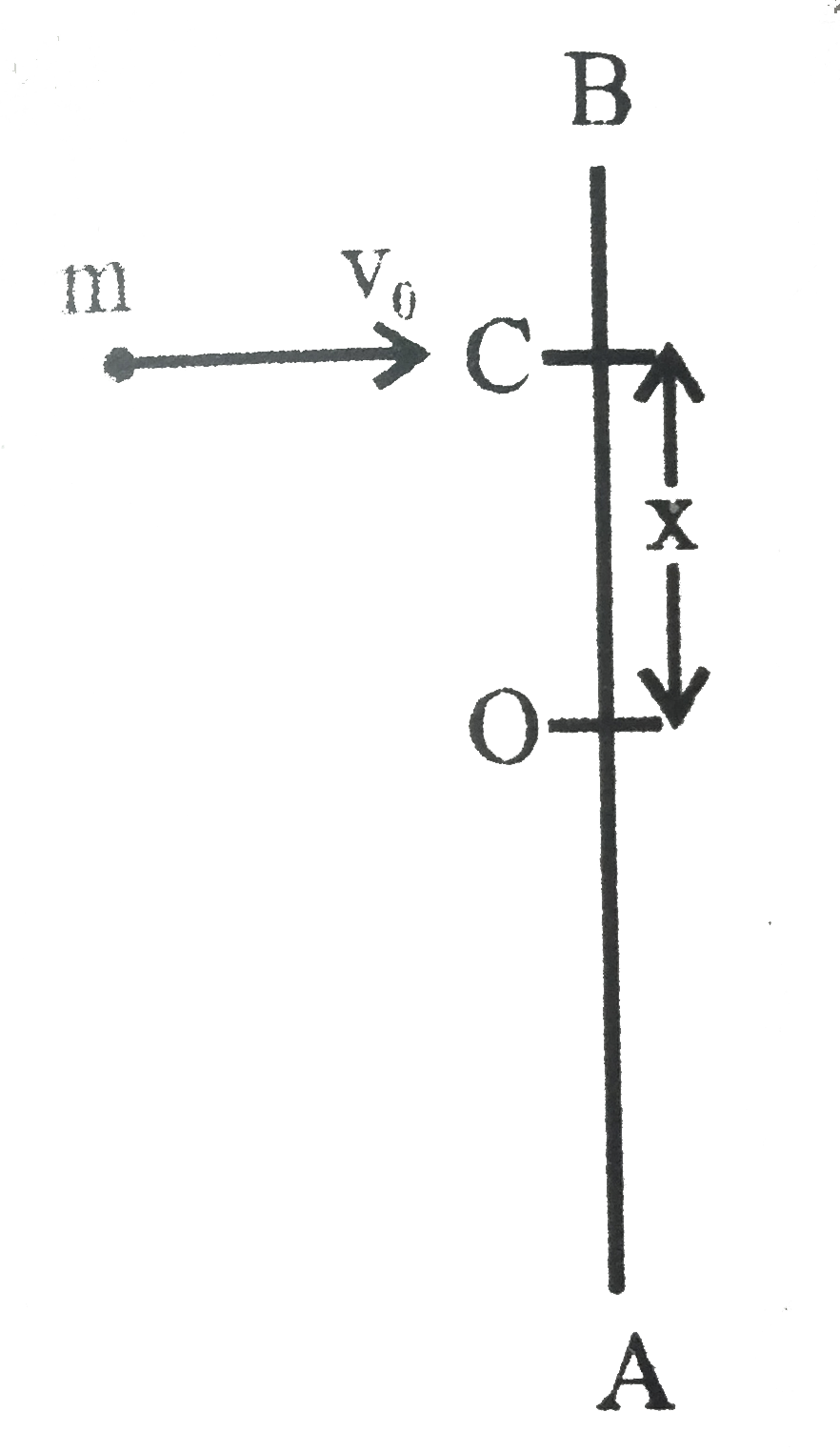 .View Solution
.View SolutionQuestion 54
A uniform rod of mass m and lkength 2a lies at rest on rotating with angular speed ω0=40rad/s is placed between two smooth walls on a rough ground. Distance between the walls is slightly greater than the diameter of the sphere . Cofficent of friction between the sphere and the ground is μ=0.1. Sphere will stop rotating after time t=.......s.View SolutionQuestion 55
A solid sphere of mass 5 kg and and radius 1 m after rotating with angular speed ω0=40rad/s is placed between two smooth walls on a rough ground. Distance between the walls is slightely greater than the diameter of the sphere. Coffiecient of friction between the sphere and the ground is μ=0.1. sphere will stop rtotating after time t = ...........s .
 View Solution
View SolutionQuestion 60
Uniform rod Ab is hinged at the end A in the figure. The other end of the rod is connected toa block through a massless string as shown. The pulley is smooth and massless. Masses of the block and the rod are same and are equal to 'm'. Acceleration due to gravity is g. The tension in the thread and angular acceleration of the rod just after releases of block from this position are
 View Solution
View SolutionQuestion 61
A uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time Δt along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).
 View Solution
View SolutionQuestion 62
A uniform rectangular plate of mass m which is free to rotate about the smooth vwerticle hinge passing through the centre and perpendicular to the plate, is lying on a smooth horizontal surface. A particle of mass m is moving with speed 'u' collides with the plate and sticks to it as shown in figure. The angular velocity of the platye after colli9sion will be
 View Solution
View SolutionQuestion 64
A Particle is attached to the lower end of a uniform rod which is hinged at its other end as shown in the figure. The minimum speed given to the particle so that the rod performs circular motion in a verticle plane will be [length of the rod is l, consider masses of bopth rod and particle to be same]
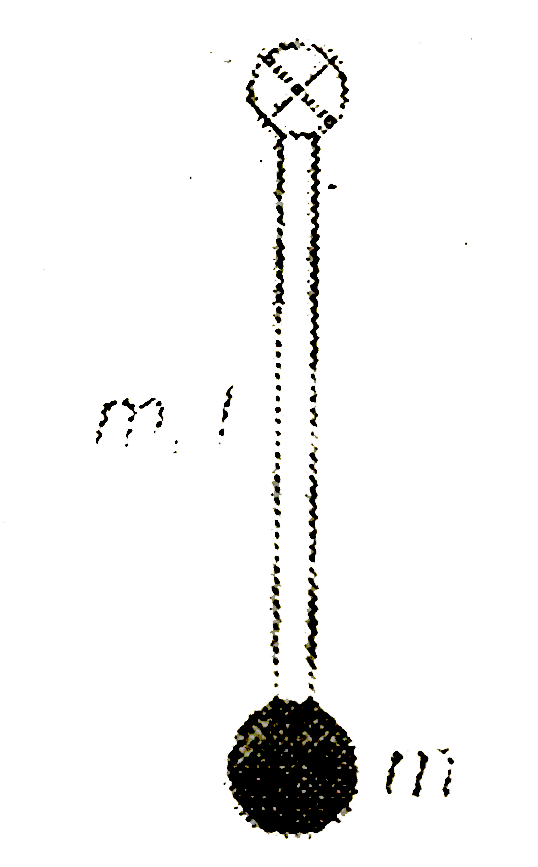 View Solution
View SolutionQuestion 65
An equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
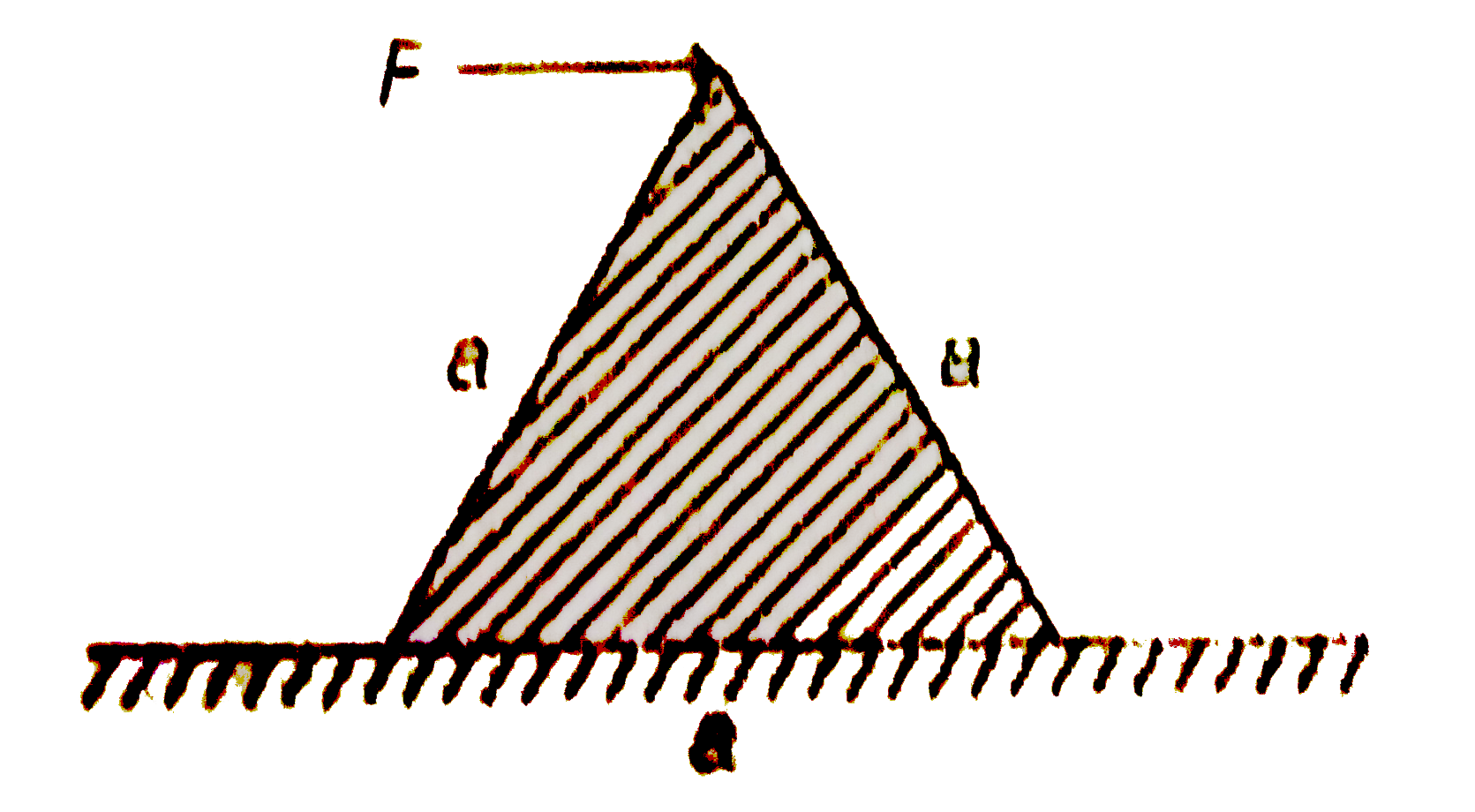 View Solution
View SolutionQuestion 66
A sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass 'm'. The co-efficent of friction between the two is μ. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of sphere relative to the plank will be
 View Solution
View SolutionQuestion 68
A rod of negligble mass and length l is pioveted at its centre. A particle of mass m is fixed to its left end and another particle of mass 2 m is fixed to the right end. If the system is released from rest and after sometime becomes vericle, The speed v of the two mases and angular velocity at that instant are
 View Solution
View SolutionQuestion 70
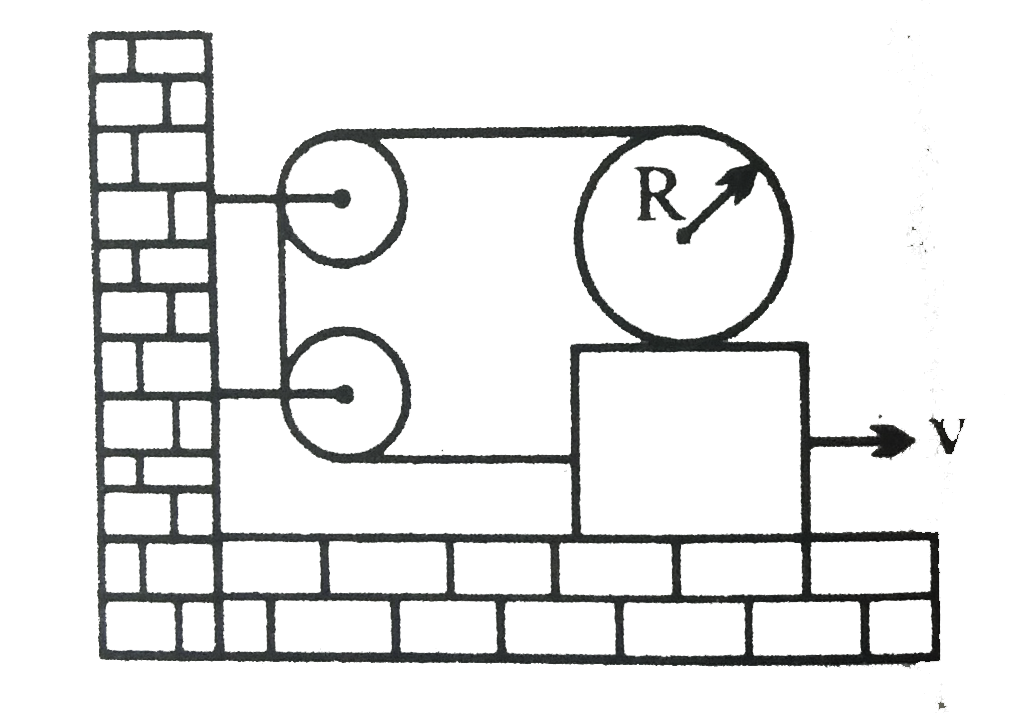
A system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are V and 2V, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
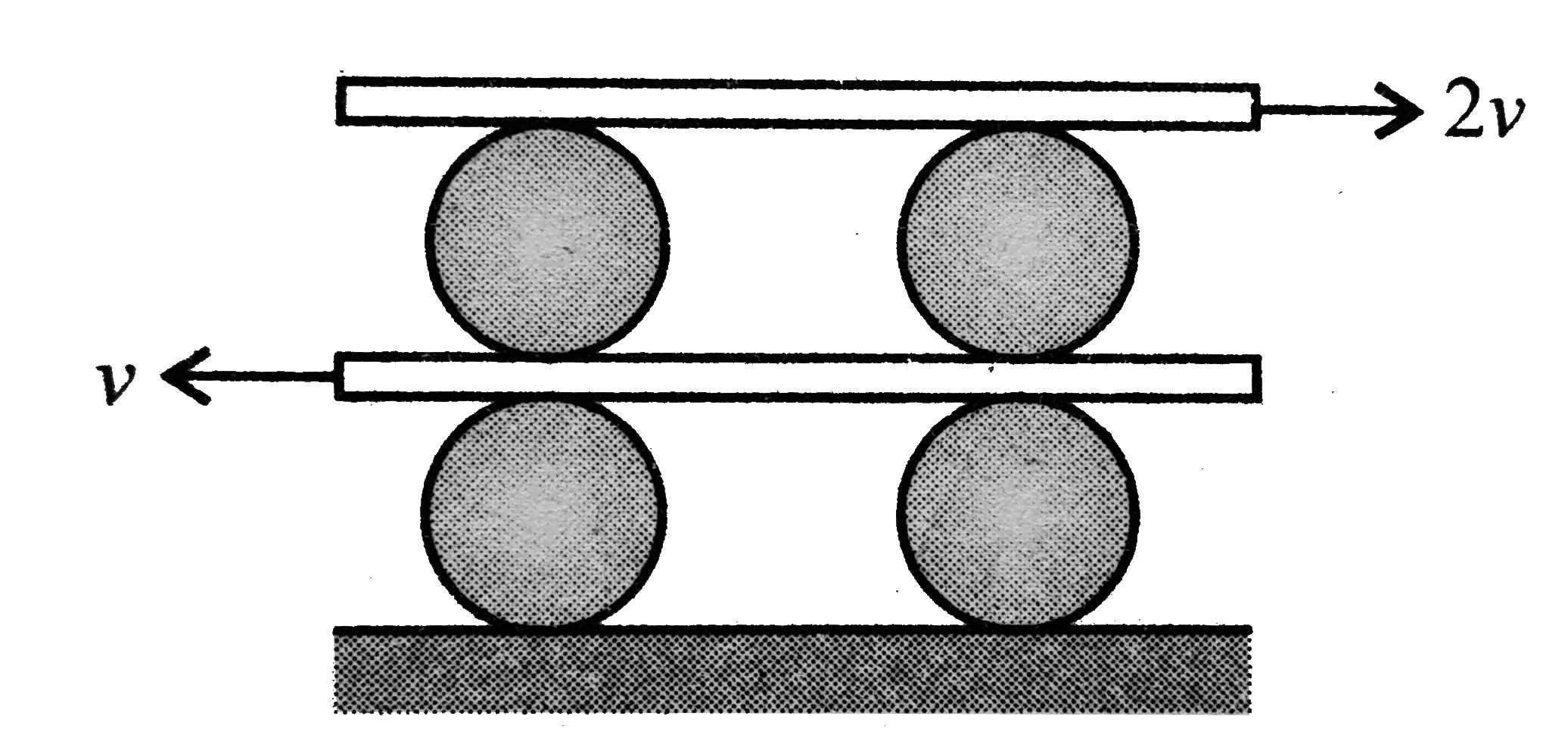 View Solution
View SolutionQuestion 74
A uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is View SolutionQuestion 75
A rod lying on a frictionless horizontal surface is initially given an anglular velocity ω about vertical axis which passes through center of mass. The centre of mass is at rest but not fixed. The length of the rod is L. Subsequently, end A of the rod collides with nail P, which is near to A such that end A becomes stationery immediately after impact. Velocity of end B just after collision will be
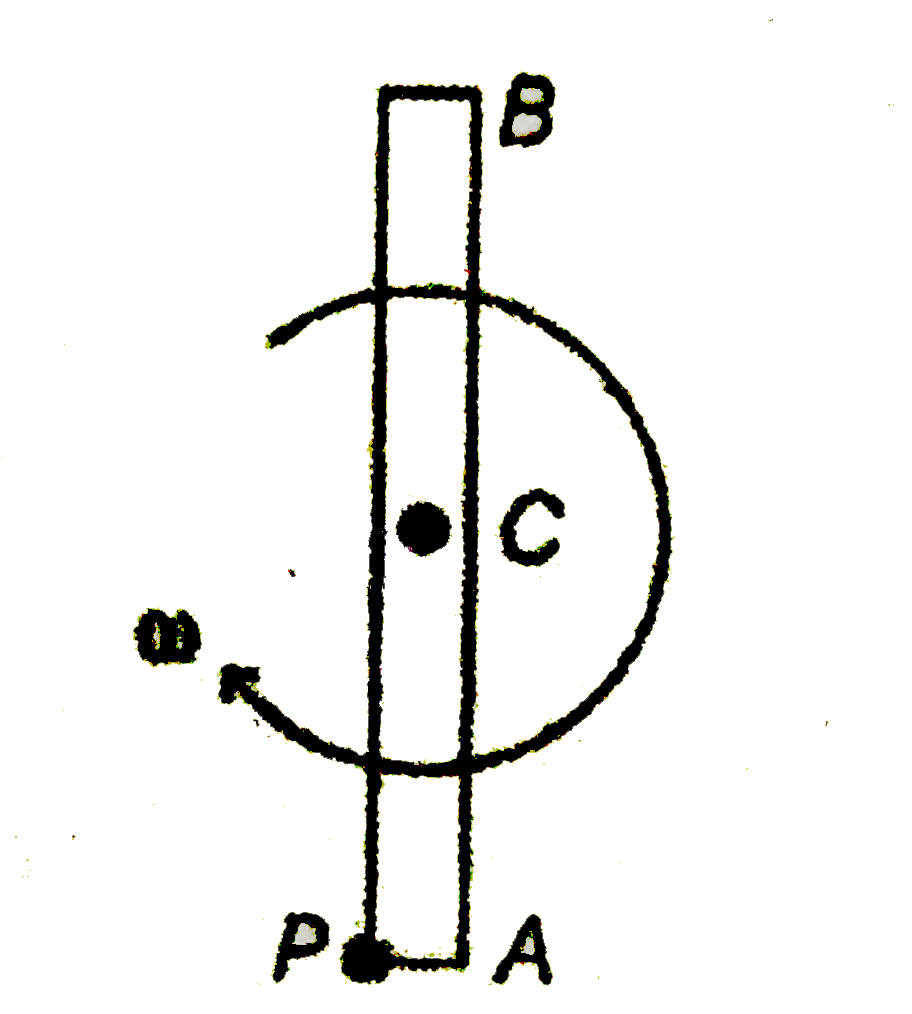 View Solution
View SolutionQuestion 78
A disc of mass M and radius R is placed on a rough horizontald surface. A light rod of length 2R is fixed to the disc at pointt A as shown in figure and force 32 Mg is applied at the other end of the rod. Find the minimum value of coefficient of friction (upto on decimal place ) between disc and horizontal surface, so that disc starts to roll without slipping .
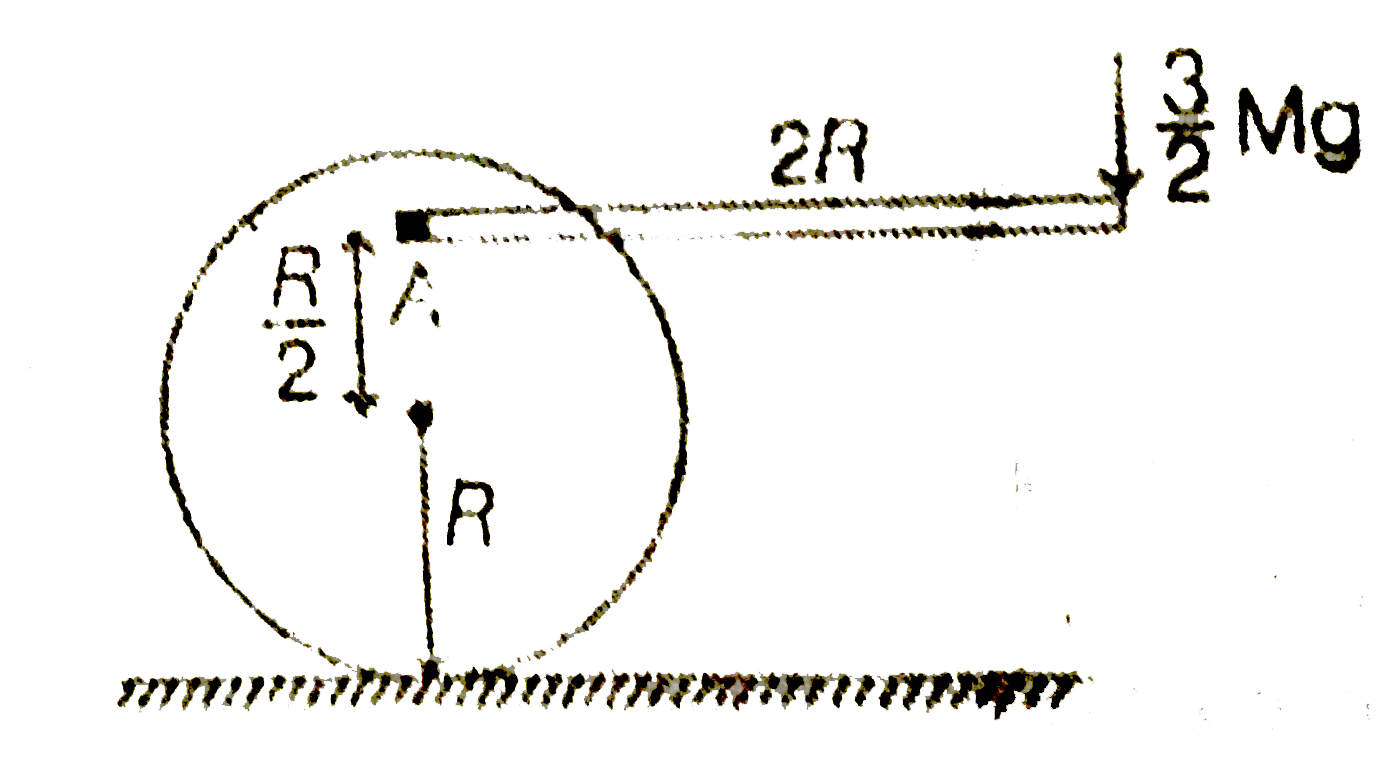 View Solution
View SolutionQuestion 79
A uniform rod of mass m , length l moving with a velocity v ( perpendicular to its length ) on a smooth horizontal plane, encounters a fixed peg P at a distance l/4 from its nearer end. The rod collides with the peg. The duration of impact Δt is very small. The average force exerted by the peg on the rod during the impact is of magnitude.
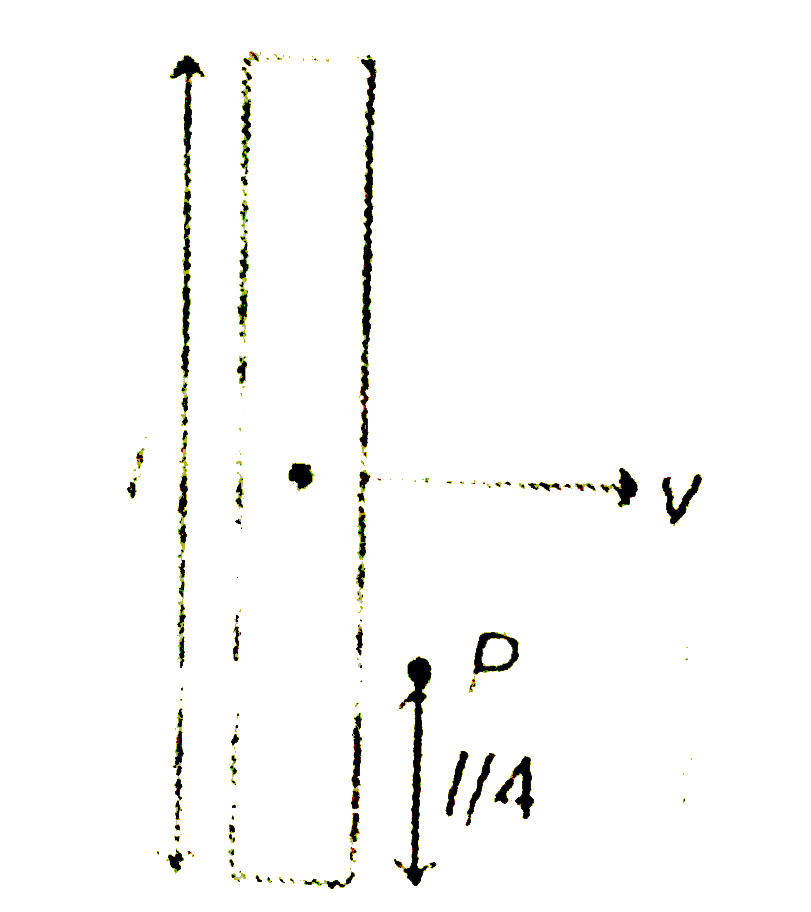 View Solution
View SolutionQuestion 80
An ideal inextensible string is wrapped over the disc of mass m and radius R. The other end of the string is connected to mass m. the string is passing over an ideal pulley A as shown in the figure. At any time t, mass m and disc are moving downward with acceleration of magnitude a1 and a2 respectively. The disc is rotating clockwise with angular acceleration of magnitude α . There is no slipping betweeb string and disc. choose the incorrect option
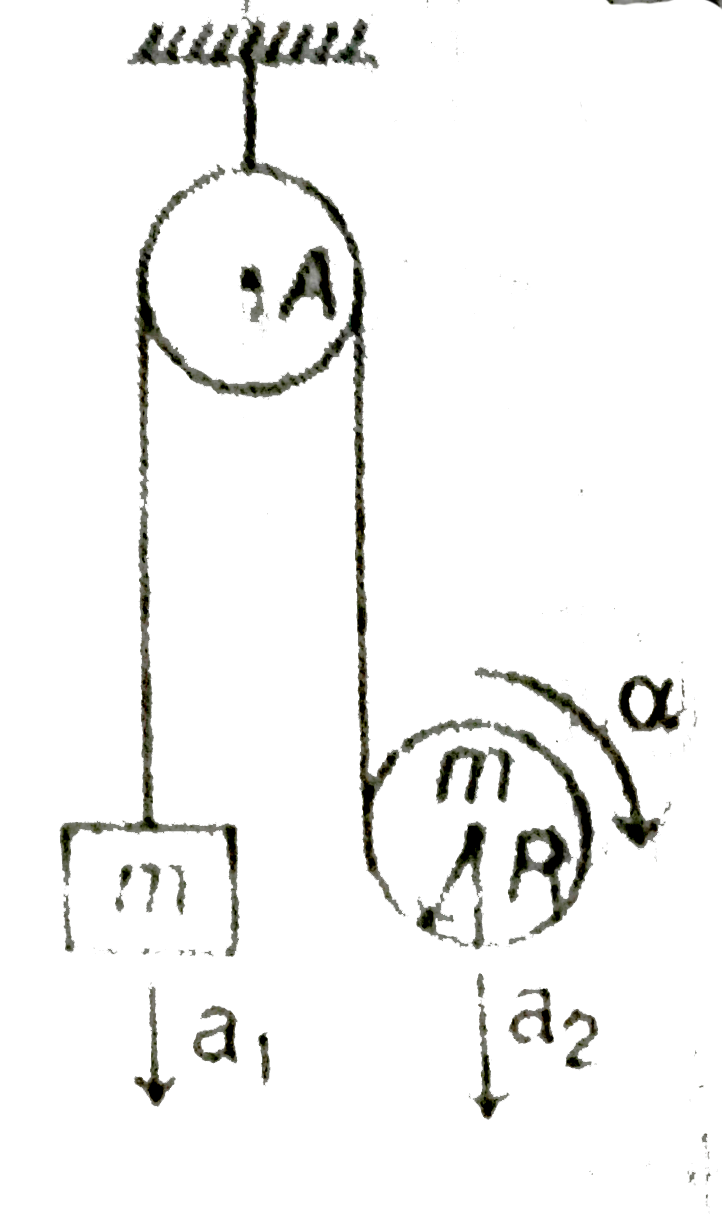 View Solution
View SolutionQuestion 81

A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View SolutionQuestion 82
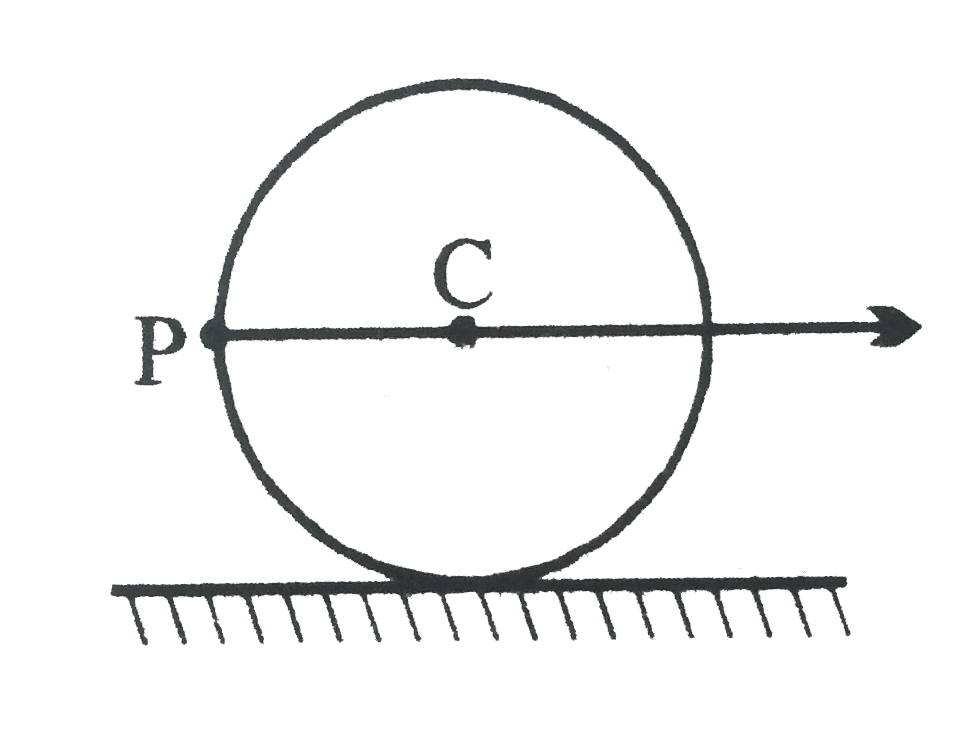
The wheel of radius R rolls wihtout slipping on horizontal rough surface and its centre O has an acceleration a0 in forward direction. A point P on the wheel is a distance r from O and angular position θ from horizontal. Find the angle θ for which point P can have zero acceleration in this position .
 View Solution
View SolutionQuestion 83
A string is warapped around a cylinder of mass m and radius r. The string is also connected to a block of same mass m with the help of another pulley as shown in figure. The angular acceleration of the cylinder is ( friction is sufficient for rolling ) ( all pulleys are ideal)
 View Solution
View SolutionQuestion 85
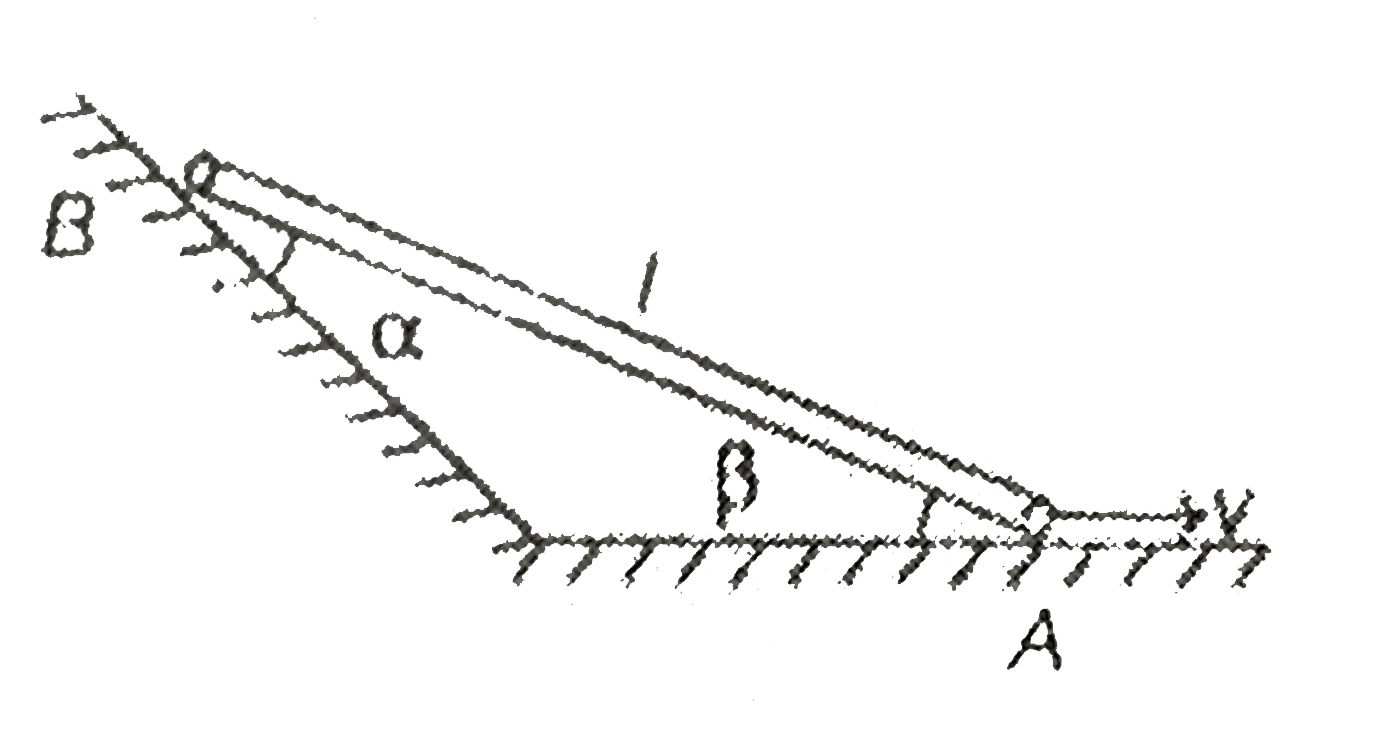
A small disc is released from rest at A on an inclined plane AB so that it rolls down wihtout slipping. It reaches the bottom with linear velocity v1 in time t1. Next a small ring released form rest on the inclined plane AC so that it rolls down without slipping. It reaches the bottom with linear vlocity v2 in time t2. Given θ1=30∘,θ2=60∘, and h=10m. Then,
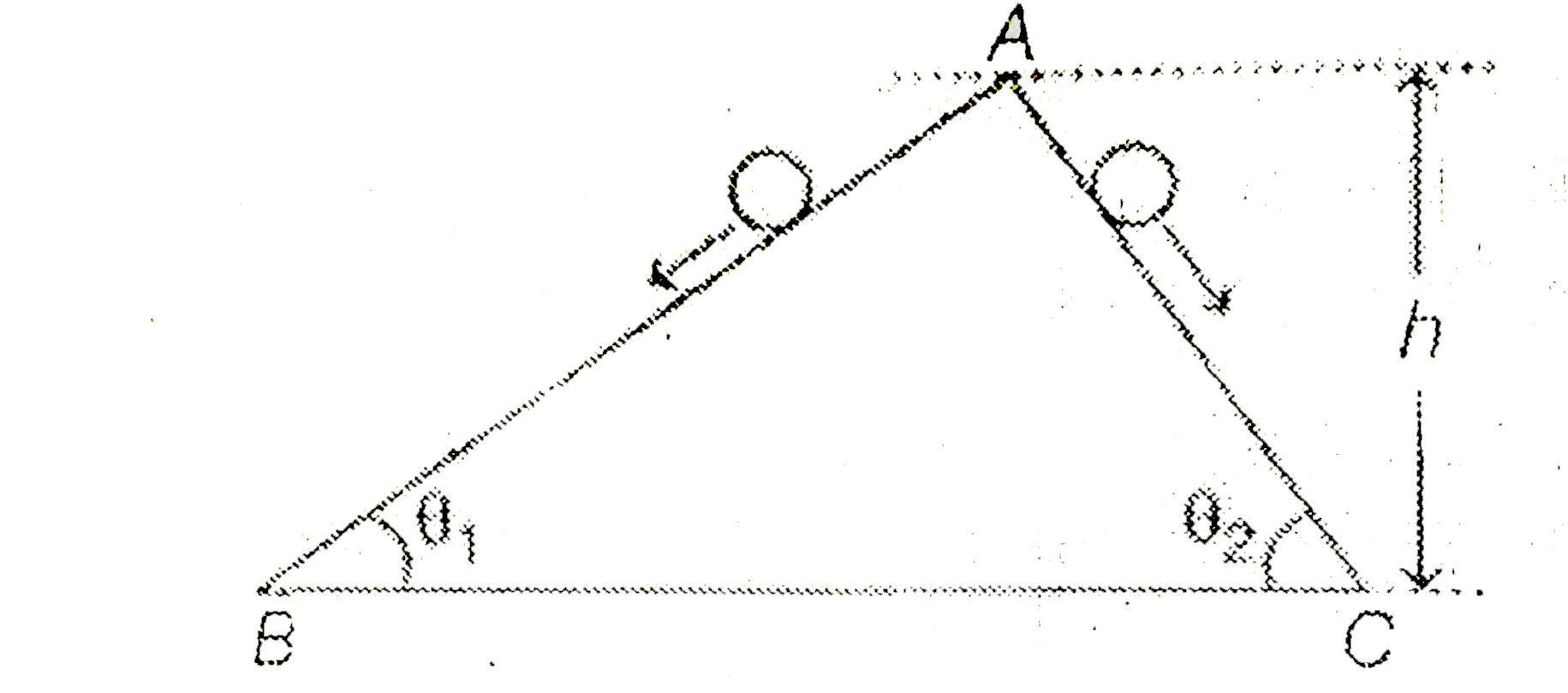 View Solution
View SolutionQuestion 86
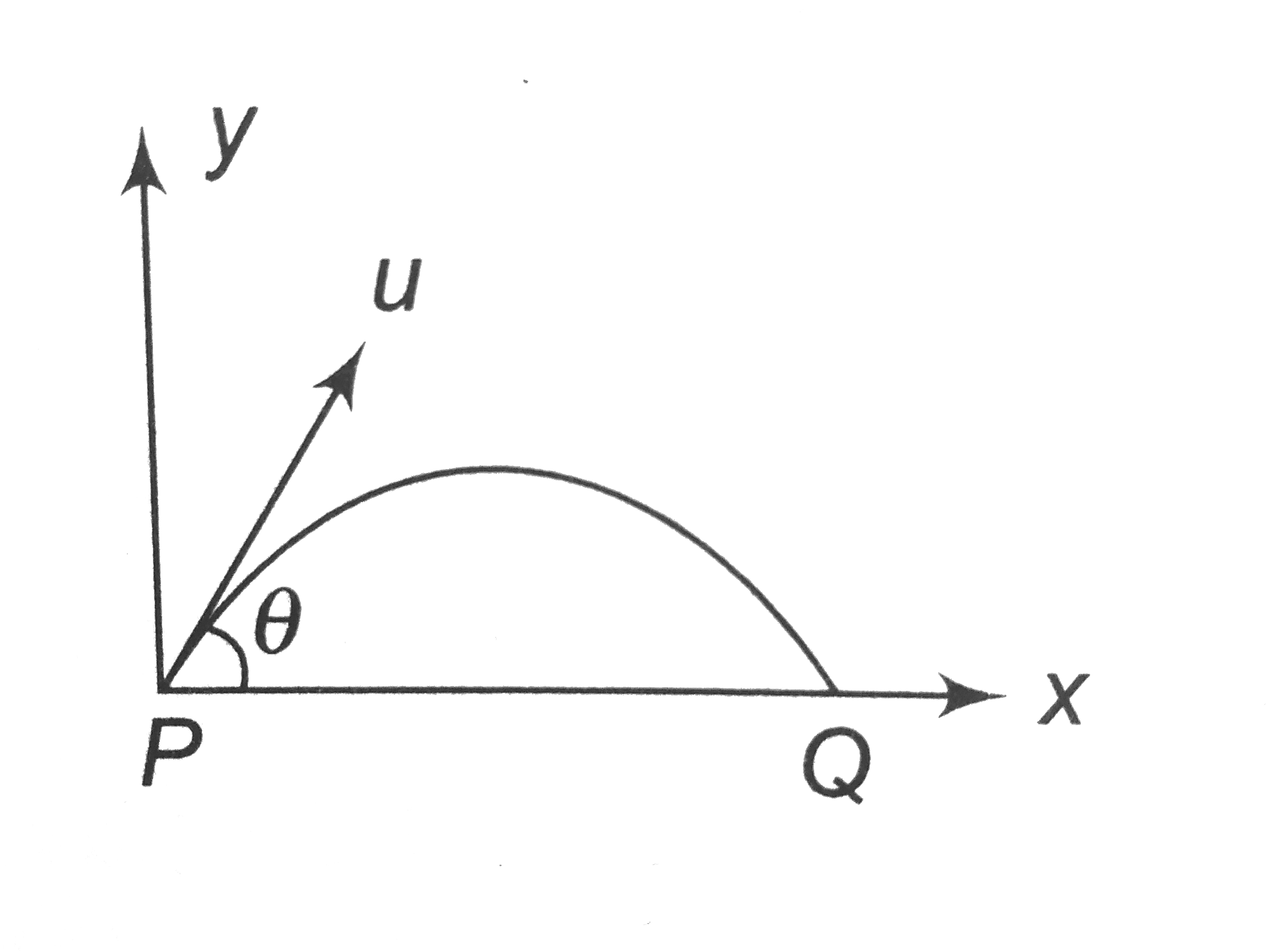
A solid ball is realeased from rest down inclines of various inclination angle θ but through a fixed vertical height h. The coefficient of static and kinetic friction are both equal to μ. Which of the following graph best represents the total kinetic energy K of the ball at the bottom of the incline as a function of the angle θ of the incline?View Solution

 .
.
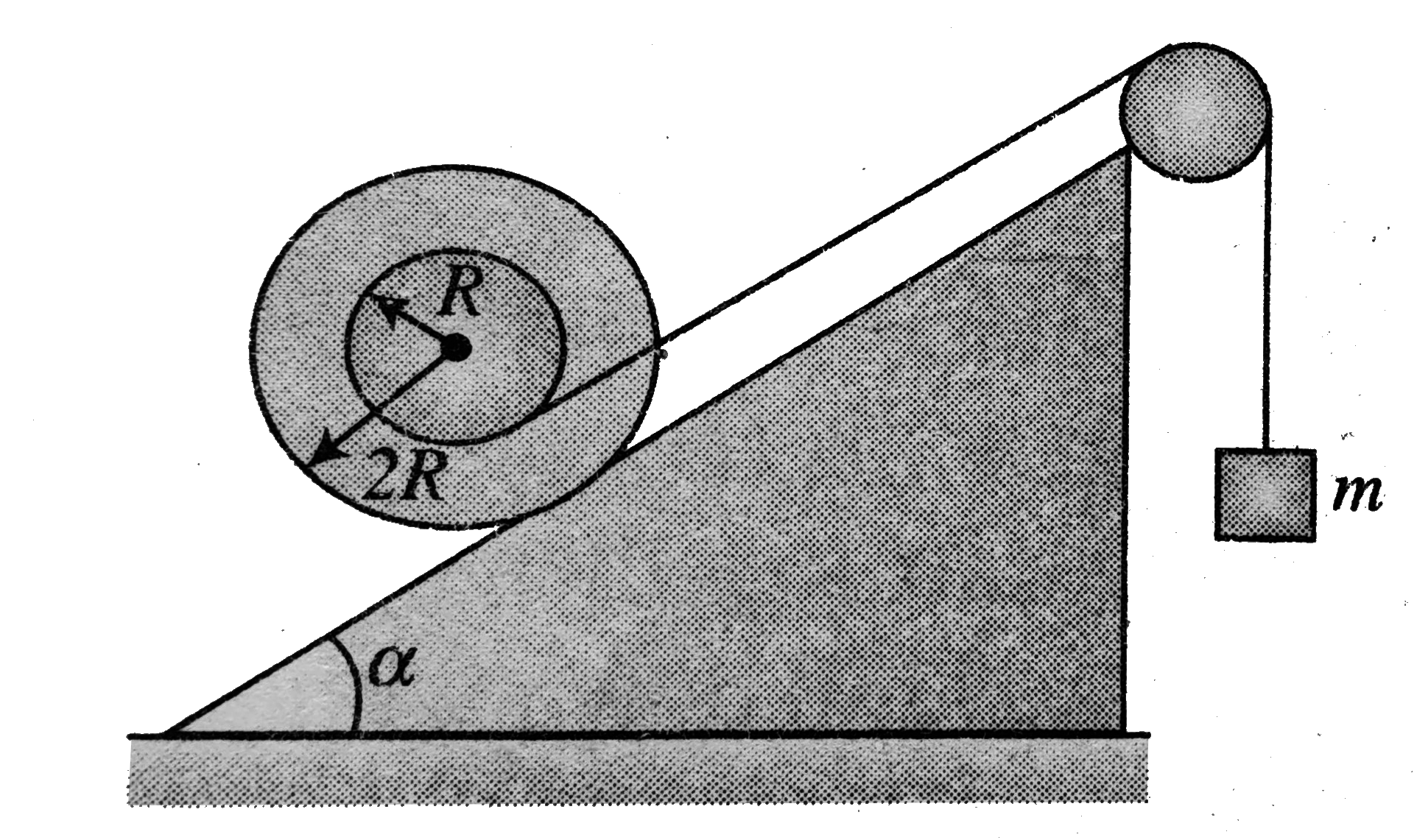



 .
.


 .
.






 .
. .
.


 .
.





 .
.