Practice exercise from GK PUBLICATIONS PHYSICS Chapter 6 RIGID BODIES AND ROTATIONAL MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | RIGID BODIES AND ROTATIONAL MOTION |
| GK PUBLICATIONS PHYSICS | Practice exercise |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
Calculate the moment of inertia of a rod whose linear density changes from ρ to ηρ from the thinner end to the thicker end. The mass of the rod is equal to M and length L. Consider the axis of rotation perpendicular to the rod and passing through the thinner end. Express your answer in terms of M,L and η .
[16ML23η+1η+1]View SolutionQuestion 6
On the flat surface of a disc of radius aa small circular hole of radius b is made with its centre at a distance c from the centre of the disc. If mass of the whole un cut disc is M, calculate the moment of inertia of the holed disc about the axis of the circular hole.
[12[a2+2c2−b4a2]] View SolutionQuestion 9
A uniform solid. cylinder A of mass m1 can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
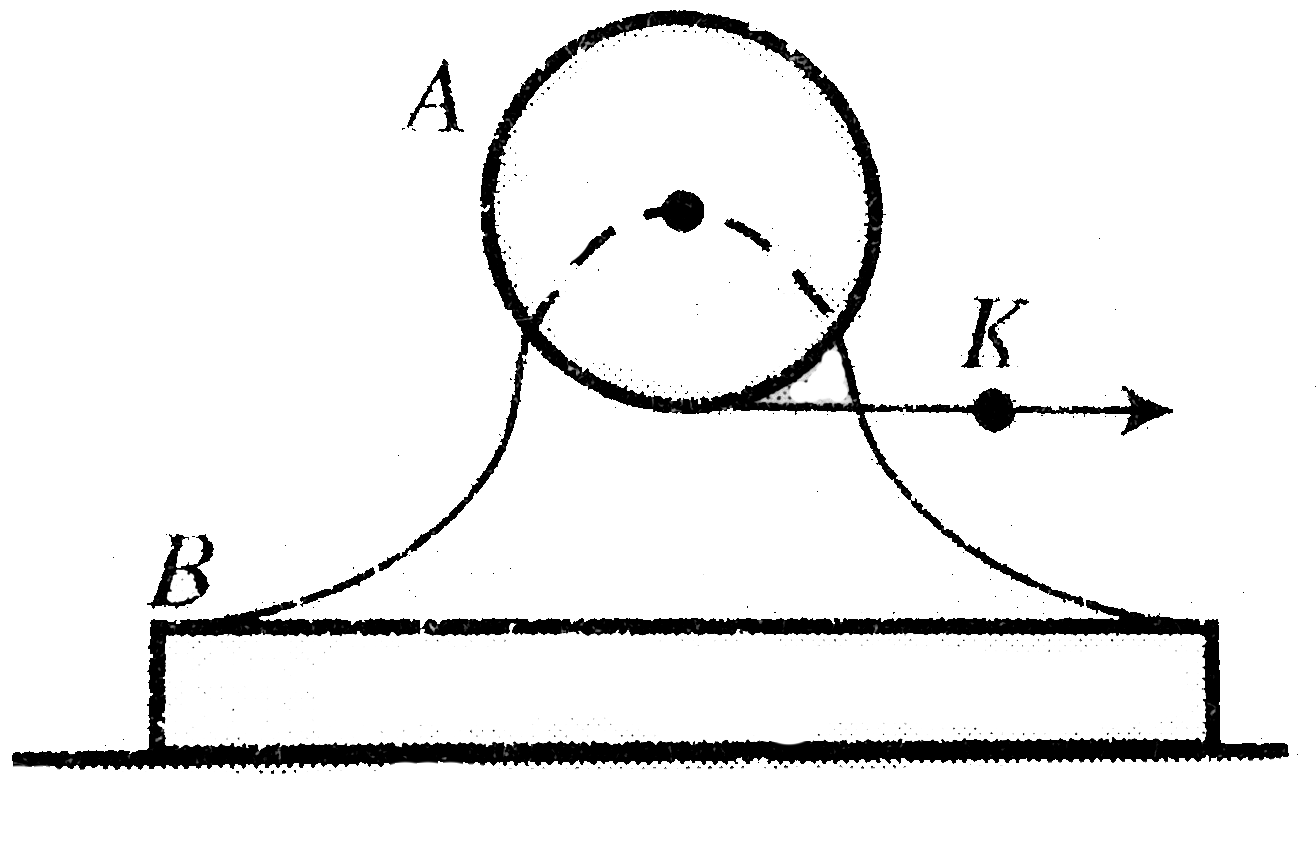 View Solution
View SolutionQuestion 11
Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
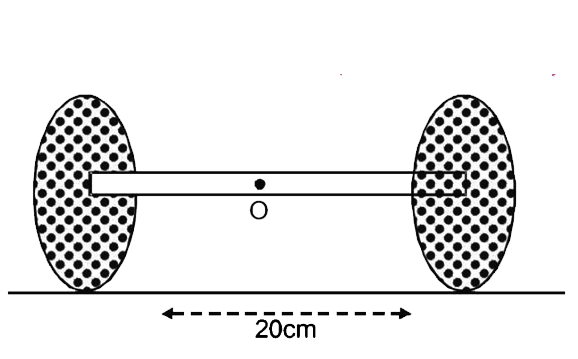 View Solution
View SolutionQuestion 14
A uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be regarded as uniform. View SolutionQuestion 15
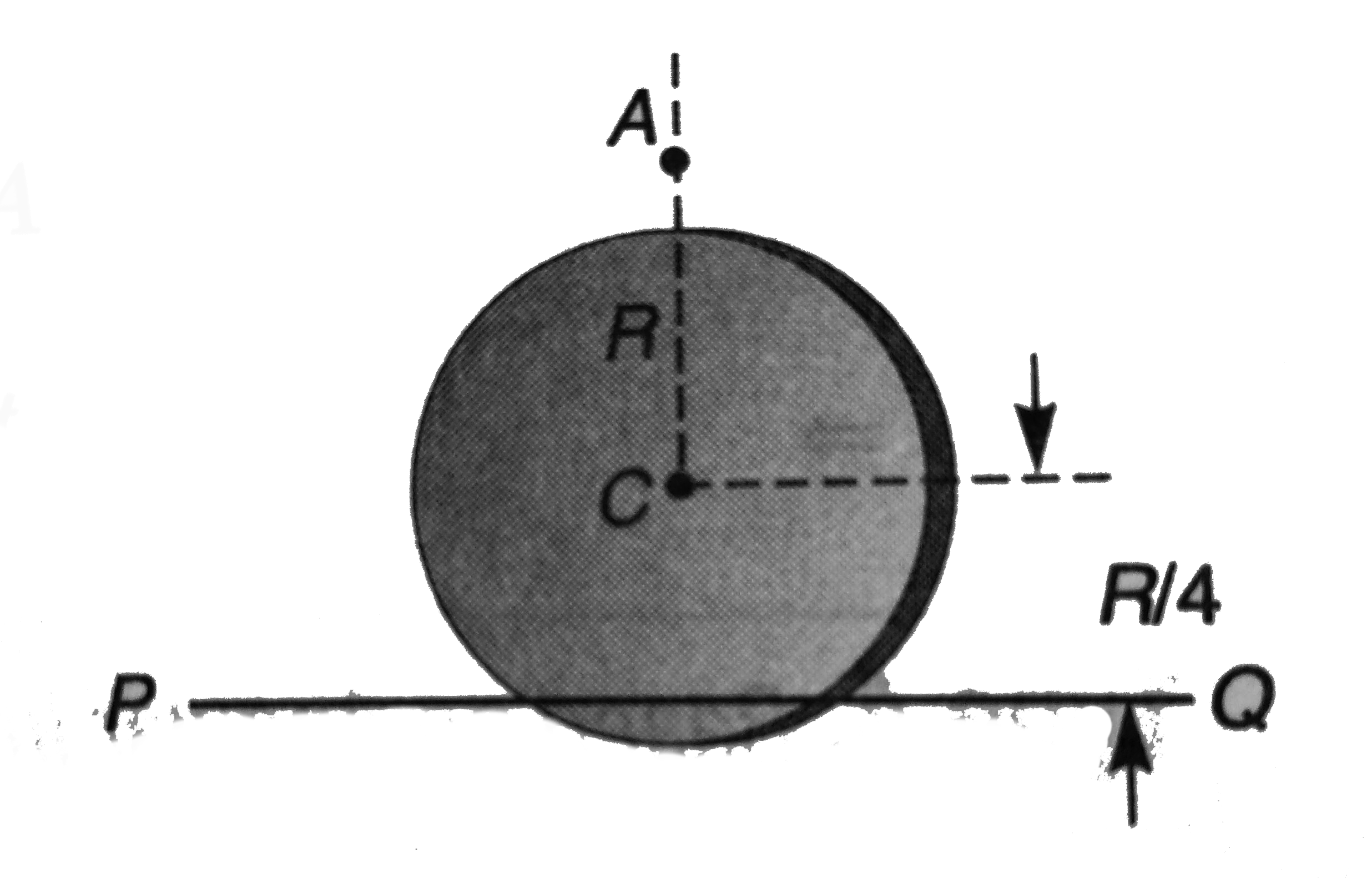
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position. View SolutionQuestion 16
A wheel of radius 6cm is mounted so as to rotate about a horizontal axis through its centre. A string of negligibe mass wrapped round its circumference carries a mass of 0.2kg attached to its free end. When let to fall, the mass descends through 1m in 5s. Calculate the angular acceleration of the wheel, its moment of inertia and tension in the cord.View SolutionQuestion 17
A uniform solid cylinder of mass M and radius 2R rests on a horizontal table top. A string attached to it runs over a pulley (disc) of mass M and radius R thatis mounted on a frictionless axle through its centre. A block of mass M is suspended from the free end of the string. The string doesn't slip over the pulley surface, and the cylinder rolls without slipping on the, table top. Find the acceleration of the block.

[g/3] View SolutionQuestion 18
As shown in figure-5.72 the solid disc and pulley have the same radii and same mass distribution. The solid disc, pulley and the block have equal masses. The plane has a slope of 30∘.The disc rolls on the incline without slipping or loss of energy. Find the acceleration of the hanging block. Consider there is no shipping of string over pulley surface. Take g= 10 m/s2.
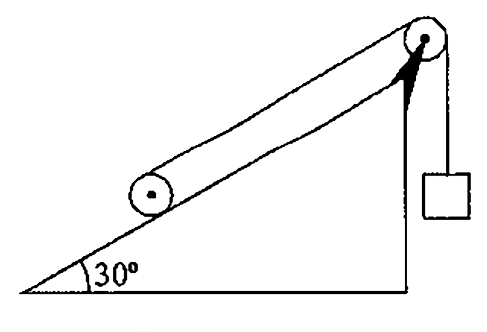 View Solution
View SolutionQuestion 19
The axis of a cylinder of radius R and moment of inertia about its axis I is fixed at centre O as shown in figure - 5.73 . Its highest point A is in level with two plane horizontal surfaces . A block of mass M is initially moving to the right without friction with speed v1 . It passes over the cylinder to the dotted position . calculate the speed v2 in the dotted position and the angular velocity acquired by the cylinder . if at the time of detaching from cylinder block stops slipping on it .
⎡⎢ ⎢⎣v11+IMR2,v1R(1+IMR2)⎤⎥ ⎥⎦
 View Solution
View SolutionQuestion 20
A spool of thread of mass m is placed on an inclined smooth plane set at an angleθ to the horizontal. The free end of the thread is attached to the wall as shown in figure-5.74. Calculate the acceleration of the centre of mass of the spool , if its moment of inertia about its axis is Iand the radius of the wound thread layer is r.
⎡⎢⎣g sinθ1+Imr2⎤⎥⎦
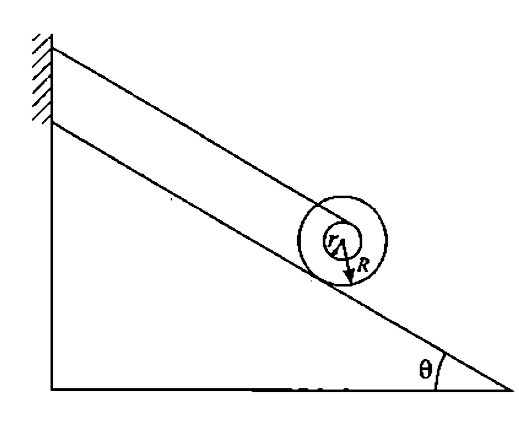 View Solution
View SolutionQuestion 21
A uniform solid cylinder of mass M and radius R rolls a rough inclined plane with its axis perpendicular to the line of greatest slope as shown in figure-5.75. As the cylinder rolls it winds up a light string which passes over a light and smooth pulley and attached to a mass m , the part of the string between pulley and cylinder being parallel to the line of greatest slope. Prove that the tension in the string is
T=[(3+4sinθ)Mmg3M+8m]
 View Solution
View SolutionQuestion 23
A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
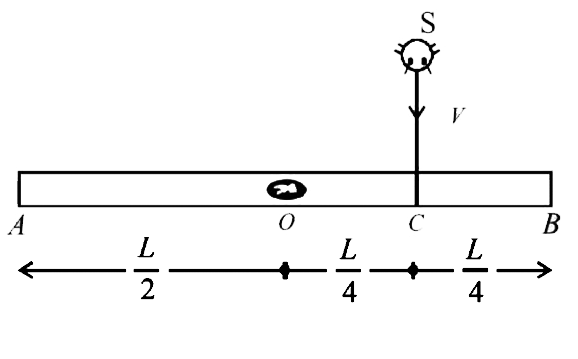 View Solution
View SolutionQuestion 24
A plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere? View SolutionQuestion 25
A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................View SolutionQuestion 26
A uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.View SolutionQuestion 27

A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its backward slipping eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.View SolutionQuestion 28
A hollow sphere is released from the top of an inlcined plane of inclination θ. A. What should be the minimum coefficientof friction between the shphere and the plane to prevent sliding? B. Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part a.View SolutionQuestion 29
A solid wooden door 1 m wide and 2 m high is hinged along one side and has a total mass of 50 kg . Initially open and at rest , the door is struck at its centre by a handful of sticky and mud of mass 0.5 kg travelling at 12 m/s just before impact . Find the final angular velocity of the door .
[72403 rad/s]View SolutionQuestion 30
A thin uniform square plate with side l and mass M can rotate freely abouta stationary vertical axis coinciding with one of its sides . A small ball of mass m flying with velocity v at right angles to the plate strikes elastically to the centre of it. Find the velocity of the ball v'after the impact and the horizontal component of the force which the axis will exert on the plate after the impact.
[3m−4M3m+4Mv,72Mm2v2l(3m+4m)2] View SolutionQuestion 31
A small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
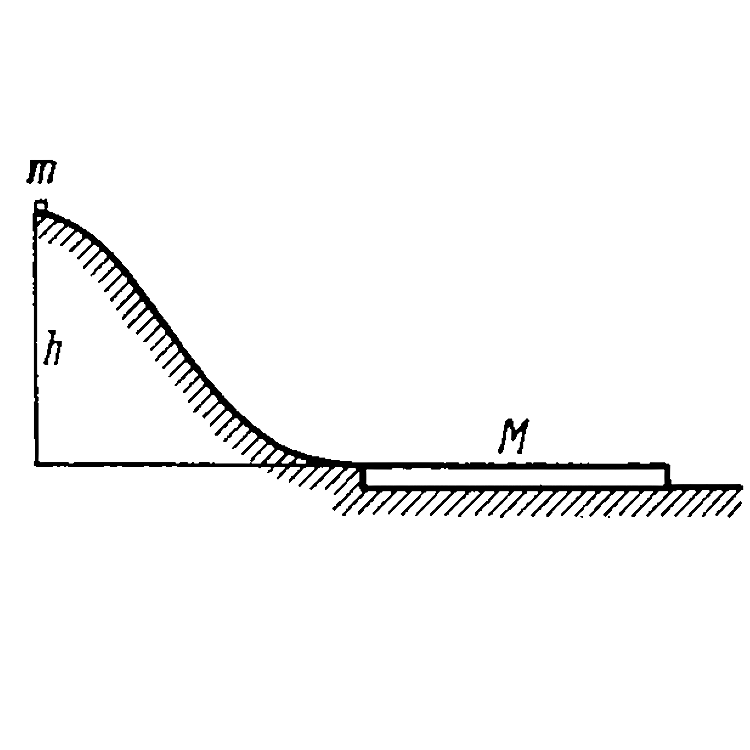 View Solution
View SolutionQuestion 32
A man of mass m1 stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre . The man walks along the edge of the disc through angle θ relative to the disc and then stops . find the angle through which the disc turned the time the man stopped .
[2m1θ2m1+m2]View SolutionQuestion 33
A uniform rod AB of length 2l and mass 2m is suspended freely at A and hangs vertically at rest when a particle of mass m is fired horizontally with speed v to strike the rod at its mid point. If the particle is brought to rest by the impact , find : (a) the impulsive reaction at A , (b) the initial angular speed of the rod and (c) the maximum angle the rod makes with the vertical in the subsequent motion .
[mv/4 , 3v/8l , cos−1(1−3v232lg)]View Solution



 .
.