Exercise from HC VERMA PHYSICS (HINGLISH) SPECIFIC HEAT CAPACITIES OF GASES for Class 11

Class 11	PHYSICS
Chapter	SPECIFIC HEAT CAPACITIES OF GASES
HC VERMA PHYSICS (HINGLISH)	Exercise
Medium	English
Academic Year	2023-2024

Question 1
A vessel containing one of mole of a monatomic ideal gas (molecular weight = 20 g mol_^(1)) is moving on a floor at a speed of $50 m s^{- 1}$ The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas , find the rise in its temperature . View Solution
Question 2
$5 g$ of a gas is contained in a rigid container and is heated from $15^{\circ} C \to 25^{\circ} C$ . Specific heat capacity of the gas at constant volume is $0.172 c a l g^{- 1}^\circ C^{- 1}$ and the mechanical equivalent of heat is 4.2 J cal . Calculate the change in the internal energy of the gas. View Solution
Question 3
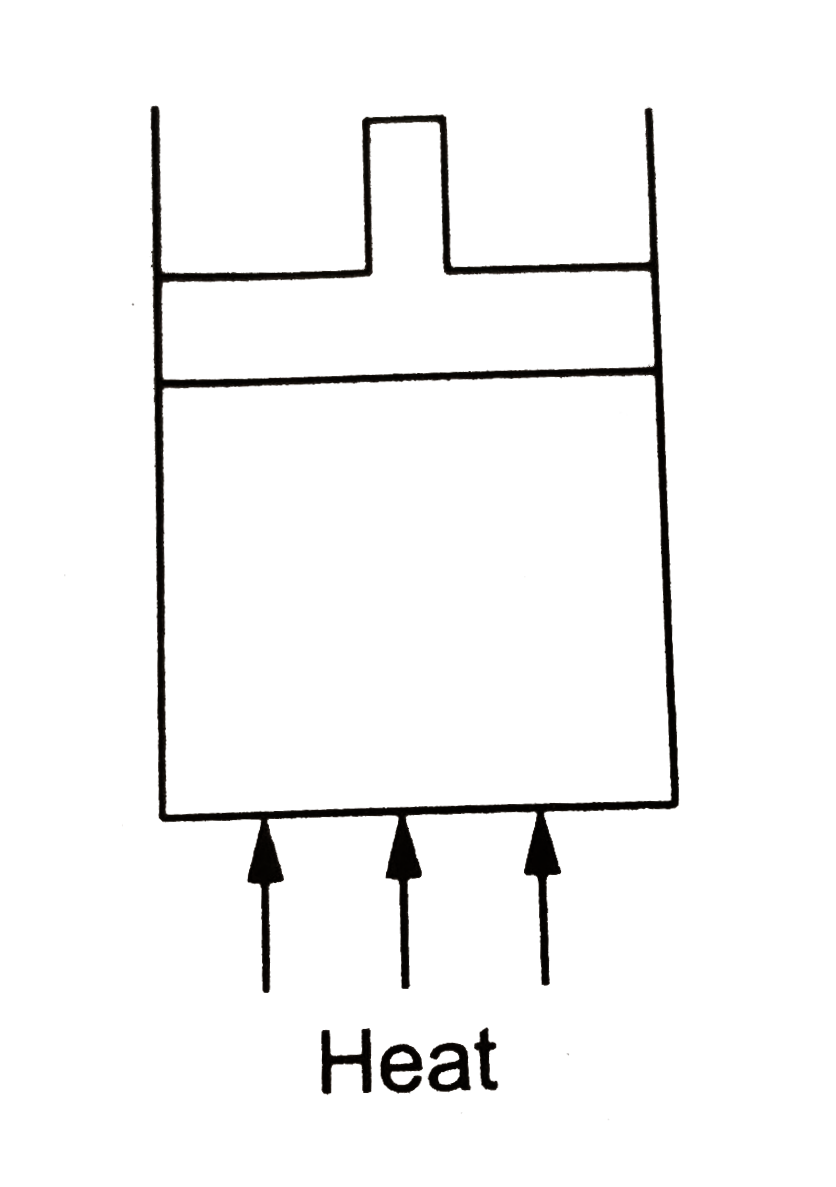
Figure shows a cylindrical container containing oxyegn $(γ = 1.4)$ and closed by a 50 kg frictionless piston. The area of cross section is $100 c m (2)$ , atmospheric pressure is $100 k P a$ +E2 and g is 10 m s^(-2). The cylinder is slowly heated for some time. Find the amount of heat supplied to gas if the piston moves out through a distsnce of 20 cm.
.View Solution
Question 4
The specific heat capacities of hydrogen at constant volume and at constant pressure are $2.4 c a l g^{- 1}^\circ C^{- 1} and 3.4 c a l g^{- 1}^\circ C$ respectively. The molecular weight of hydrogen is $2 g m o l^{- 1}$ and the gas constant $R = 8.3 \times 10^{7} e r g^{\circ} C m o l^{- 1}$ . Calculate the value of $J$ . View Solution
Question 5
The ratio of the molar heat capacities of an ideal gas is $(\frac{C_{p}}{C_{v}} \frac{7}{6})$ . Calculate the change in internal energy of 1.0mole of the gas when its temperature is raised by $50 k (a)$ keeping the pressure constant , (b) keeping the volume constant and (c ) adiabatically. View Solution
Question 6
A sample of air weighing $1.18 g$ occupies $1.0 \times 10^{3} c m^{3}$ when kept at $300 K and 1.0 \times 10^{5}$ pa. When $2.0 c a l$ of heat is added to it constant volume, its temperature increases by $1^{\circ} C$ . Calculate the amount if heat needed to increases the temperature of air by $1^{\circ} C$ at constant pressure if the mechanical equivalent of heat si $4.2 \times 10^{- 1}$ . Assume that air behaves as an ideal gas. View Solution
Question 7
An ideal gas expands from $100 c m^{3} \to 200 c m^{3}$ at a constant pressure of $2.0 \times 10^{5}$ when $50 J$ of heat is supplied to it. Calculate (a) the change in internal energy of the gas , (b) the number of moles in the gas if the initial temperature is 300K , (C ) the molar heat capacity $C_{P}$ at constant pressure and (d) the molar heat capacity $C_{v}$ at constant volume View Solution
Question 8
An amount of heat is added to a monatomic ideal gas in a process in which the gas performs work $\frac{Q}{2}$ on its surrounding. Find the molar heat capacity for the process. View Solution
Question 9
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation $p = k v$ . Show that the molar heat capacity of the gas for the process is given by $(C = C_{v} + \frac{R}{2}$ .View Solution
Question 10
An ideal gas $(\frac{C_{p}}{C_{v}} = γ)$ is taken through a process in which the pressure and volume vary as $(p = a V^{b}$ . Find the value of b for which the specific heat capacity in the process is zero. View Solution
Question 11
Two ideal gases have same value of $(\frac{C_{p}}{C_{v}} = γ)$ . What will be the value of this ratio for a mixture of the two gases in the ratio $(1 : 2)$ ? View Solution
Question 12
A mixture contains 1 mole of helium $(c_{p} = 2.5 R, C_{v} 1.5 R .)$ and 1mole of hydrogen $(C_{p} = 3.5 R, C_{v} = 2.5 R,)$ . Calculate the values of $C_{p}, C_{v} and γ$ for the mixture.View Solution
Question 13
Half mole of an ideal gas $(γ = \frac{5}{3}) i s t a k e n t h r o u g h t h e c y c \leq a b c d a a s s h o w n \in f i g u r e . T a k e$ (R = 25/3 JK^(-1) mol^(-1)) $. (a) F \in d t h e t e m p e r a t u r e o f t h e g a s \in t h e s t a e s a, b, c and d . (b) F \in d t h e a m o u n t o f h e a t \supset p l i e d \in t h e p r o c e s s e s a b and b c . (c) F \in d t h e a m o u n t o f h e a t l i b e r a t e d \in t h e p r o c e s s e s$ cd and da.
View Solution
Question 14
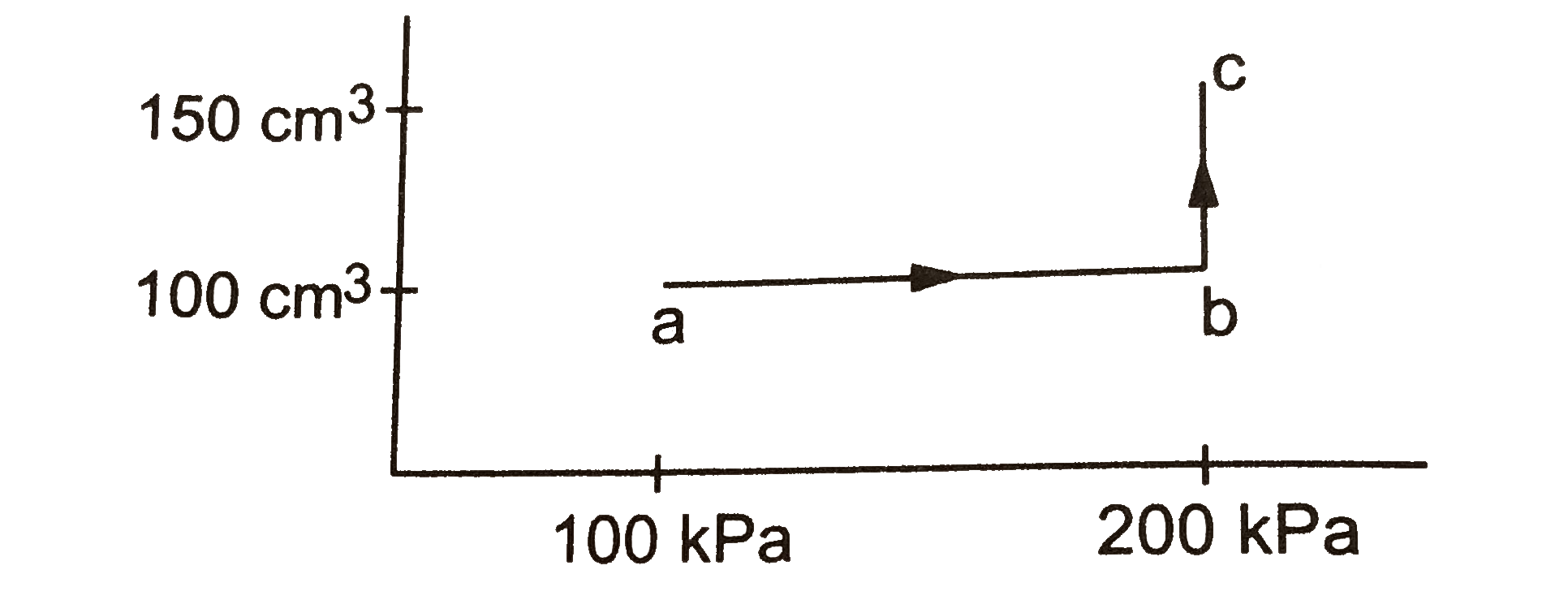
An ideal gas $(γ = 1.67)$ is taken through the process abc shown in figure . The temperature at the point a is $300 k$ . Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
View Solution
Question 15
In Joly's differential steam calorimeter, $3 g$ of an ideal gas is ccontained in a rigid closed sphere at $20^{\circ} C$ . The sphere is heated by steam at $100^{\circ} C$ and it is found that an extra $0.095 g$ of steam has condensed into water as the temperature of the gas becomes constant. Calculate the specific heat capacity of the gas in $(J g^{- 1} K^{- 1} .$ The latent heat of vaporization of $w a t e r = 540 c a l g^{- 1}$ . View Solution
Question 16
The volume of an ideal gas $(γ 1.5)$ is changed adiabatically from 4.00 liters to 3.00 liters . Find the ratio of (a) the final pressure to the initial pressure and (b) the final temperature to the initial temperature. View Solution
Question 17
An ideal gas at pressure $2.5 \times 10^{5}$ $p a$ and temperture $300 k$ occupies $100$ . It is adiabatically compressed to half its original volume. Calculate (a) the final pressure, (b) the final temperature and ( c) the work done by the gas in the peocess. Take $(γ = 1.5)$ .View Solution
Question 18
Air $(γ = 1.4)$ is pumped at 20atm pressure in a motor tyre at $20^{\circ} C$ . If the tyre suddenly bursts, what would be the temperature of the air coming out of the tyre. Neglect any mixing with the atmoshpheric air. View Solution
Question 19
A gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure , volume and temperture of the gas are $100 k p a, 400 c m^{3}$ and $300 k$ respectively. The ratio of the specific heat capacities of the gas is $(\frac{C_{p}}{C_{v}} = 1.5)$ Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to 100 cm^(3). View Solution
Question 20
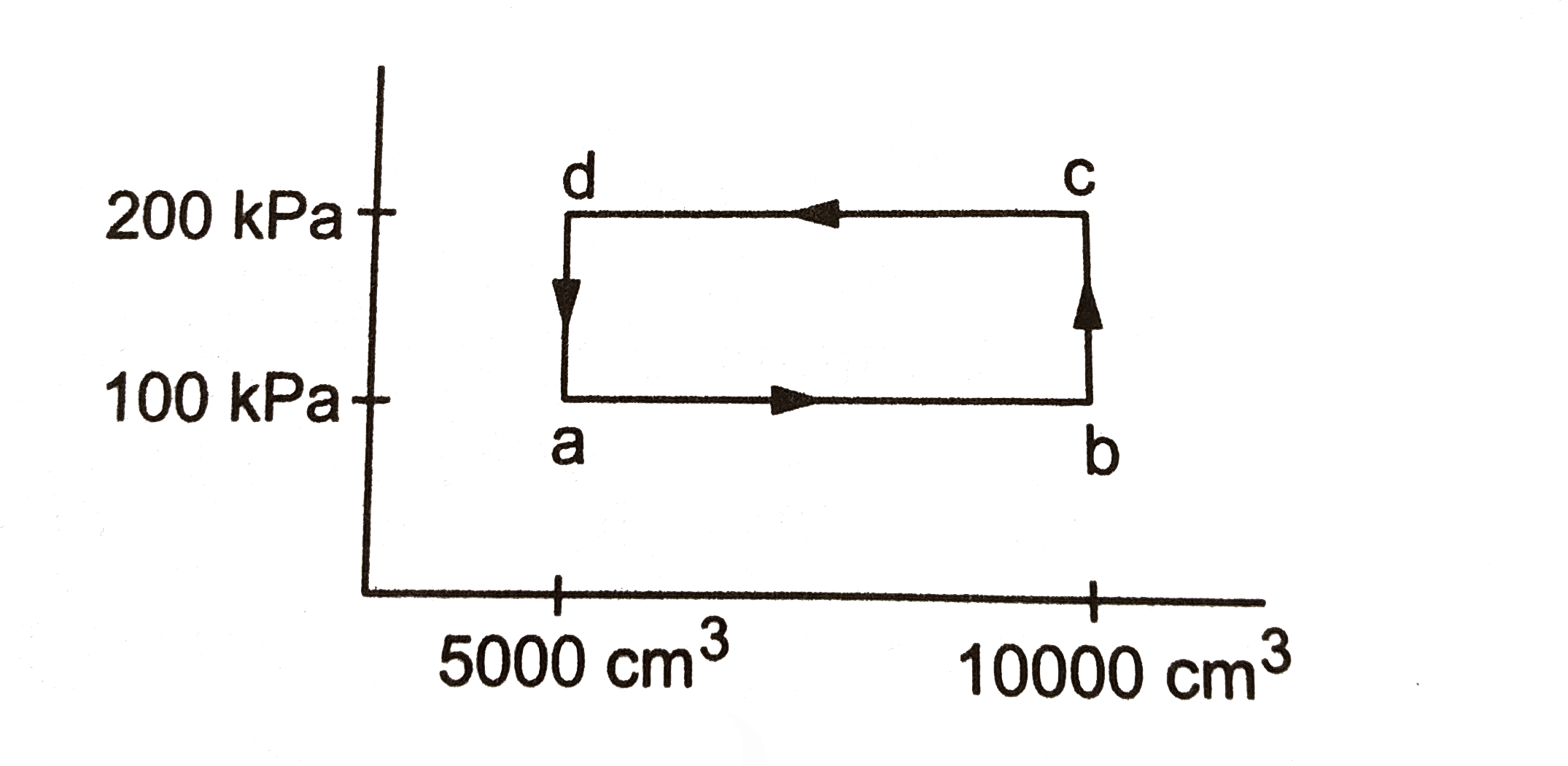
The initial pressure and volume of a given mass of a gas $(\frac{C_{p}}{C_{v}} = γ)$ are $(p_{0}) and (V_{0}) . T h e g a s c a n e x c h a n \geq h e a t w i t h s u r r o u n d \in g . (a) I t i s s l o w l y c o m p r e s s e d \to a v o l u m e$ (V_0 / 2 ) $and t h e n s u d d e n l y c o m p r e s s e d \to$ (V_0 /4) $. F \in d t h e f \in a l p r e s s u r e . (b) I f t h e g a s i s s u d d e n l y c \pm p r e s s e d o m t h e v o l u m e$ (V_0 to V_0 / 2 ) $and t h e n s l o w l y c o m p r e s s e d \to$ (V_0 / 4 ), What will be the final pressure?. View Solution
Question 21
Conider a given sample of an ideal gas $(\frac{C_{p}}{C_{v}} = γ)$ having initial pressure $(p_{0}) and v o l u m e (V_{0})$ . (a) The gas is isothermally taken to a pressure $(\frac{P_{0}}{2})$ and from there adiabatically ta a pressure $(\frac{p_{0}}{2}) and o m t h e r e i s o t h e r m a l l y \to a p r e s s u r e$ (p_0 / 4 ) . find the volume.View Solution
Question 22
A given sample of an ideal gas $(γ = 1.5)$ is compressed adiabatically from a volume of $150 c m^{3}$ to $50 c m^{3}$ . The initial pressure and the initial temperature are $150 k p a$ and $300 K$ . Find (a) the number of moles of the gas in the sample, (b) the molar heat capacity at constant volume, (c) the final pressure and temperature, (d) the work done by the gas in the process and (e) the change in internal energy of the gas . View Solution
Question 23
Three samples A, B and C of the same gas $(γ = 1.5)$ have equal volumes and temperatures. The volume of each sample is doubled, the process being isothermal for A, adiabtic for B and isobaric for C. If the final pressures are equal for the three samples, Find the ratio of the initial pressures. View Solution
Question 24
Two samples A and B of the same gas have equal volumes and pressures . The gas is sample A is expanded isothermally to double its volume and the the gas in B is expanded adibatically to double its volume . If the work done by the gas is the same for the two cases, show that gamma satisfies the equation $(1 - 2^{1 - γ} = (γ - 1) 1 n 2$ . View Solution
Question 25
1 liter of an ideal gas $(γ = 1.5)$ at $300 k$ is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is $100 k p a$ , find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature? (e) the gas is now colled to $300 k$ keeping its pressure constant. Calculate the work done during the process . (f) The gas is now expanded iasothermally to achive its original volume of 1 liters. Calculate the work done by the gas .(g) Calculate the total work done in the cycle. View Solution
Question 26
Figure shows a cylindridcal tube with a adibatic walls and fitted with an adiabatic separtor. The separator can be slid into the tube by an external mechanism. An ideal gas $(γ = 1.5)$ is injected in the two sides at equal pressures and temperatures . The separator remains in equilibrium at the middel. It is now slid to a position where it divides the tube in the ratio 1:3 Find the ratio of the tempertures in the two parts of the vessel.
View Solution
Question 27
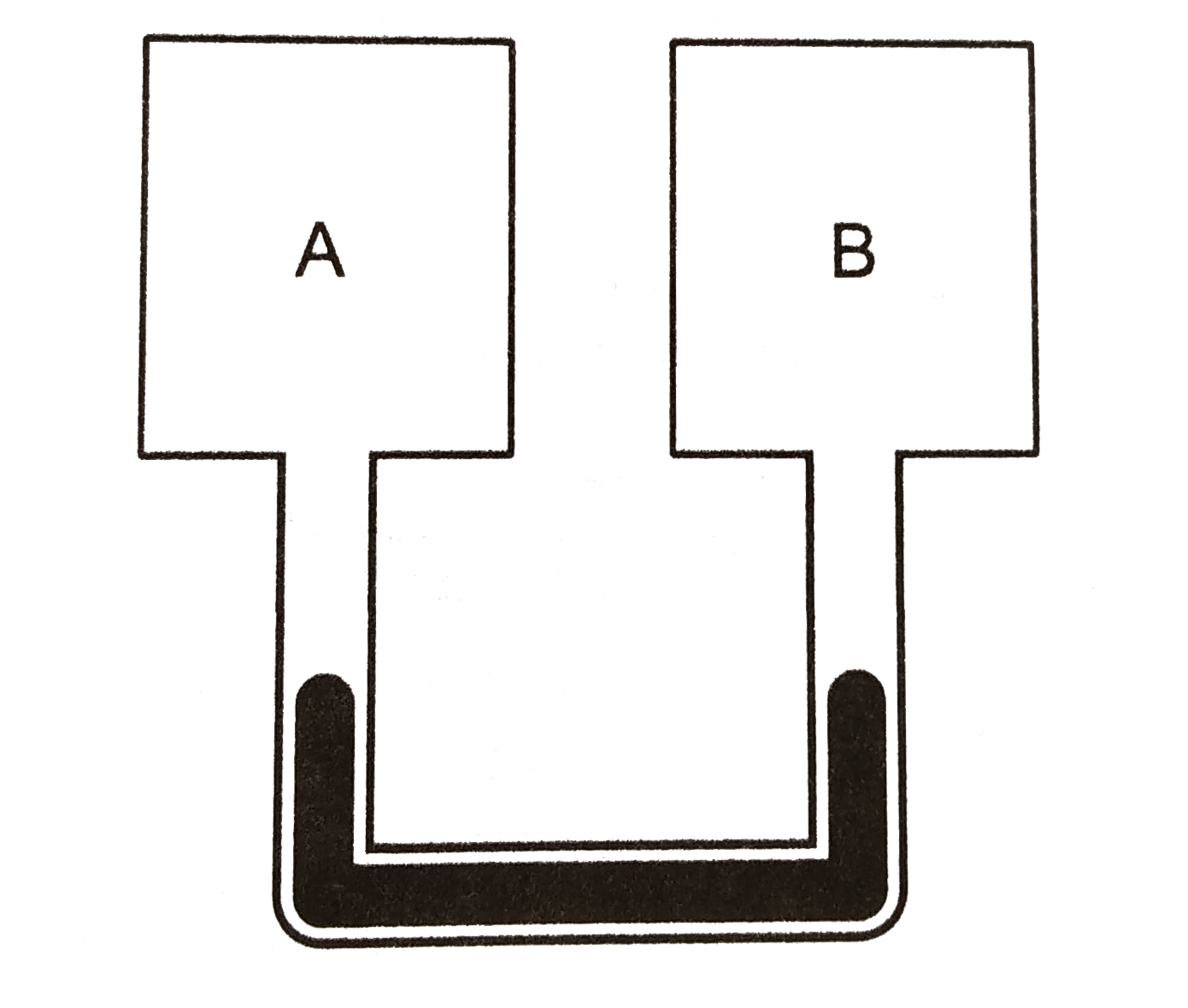
Figure shows two rigid vessels A and B, each of volume $200 c m^{3}$ containg an ideal gas $(C_{v} = 12.5 J K^{- 1} m o l^{- 1})$ . The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm mercury and the temperature is 300k. (a) $(5 - 0 J)$ of heat is supplied to the gas in the vessels.(b) $(10 J)$ to the gas in the vessels B. Assuming no appreciable transfer of heat from A to B calculate the dufference in the heights of mercury in the two sides of the manometer. Gas constant $(R = 8.3 J K^{- 1} m o l^{- 1})$
View Solution
Question 28
Figure shows two vessels with adiabatic walls, one containing 0.1 g of helium $(γ = 1.67, M = 4 g m o l^{- 1})$ and the other containing some amount of hydrogen $(γ = 1.4, M = 2 g m o l^{- 1})$ . Initially , the temperatures of the two gases are equal. The gases electrically heated for some time during which equal amounts of heat are given to the gases. It is found that the temperatures rise through the same amount in the two vessels. Calculate the mass of hydrogen.
View Solution
Question 29
Two vessels A and B of equal volume $(V_{0})$ are connected by a narrow tube which can be closed by a value. The vessels are fitted with piston which can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas $(\frac{C_{p}}{C_{v}} = γ)$ at atomspheric pressures $(P_{0})$ and atmoshpeheric temperature $(T_{0})$ . The walls of the vessels A are diathermic and those of B are adiabatic. The value is now closed and the pistons are slowly pulled out to increase the volumes of the of the vessels to dobuled the original value.(a) Find the temperatures and pressures in the two vessels. (b) The value is now opened for sufficeint time so that the gases acquire a common tempertures and pressures . Find the new values of the temperatuere and the pressures. View Solution
Question 30
Figure shows an adiabatic cylindrical tube of volume $(V_{0})$ divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure $(p_{1})$ and the temperatures $(T_{1})$ is injected into the left part and the another ideal gas at pressures $(P_{2})$ and temperature $(T_{2})$ is injected into the right part. $(\frac{C_{p}}{C_{v}} = γ)$ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.
View Solution
Question 31
An adibatic cylindrical tube of cross-sectional area $1 c m^{2}$ is closed at one end fitted with a piston at the other end. The tube contains $0.03 g$ of an ideal gas . At 1 atm pressure and at the temperture of the surrounding, the length of the gas column. The pressure of the gas falls to $0.355 a t m$ . Find th speed of sound in the gas at atmospheric temperture. View Solution
Question 32
The speed of sound in hydrogen at $0^{\circ} c$ is $1280 m s^{- 1}$ . The density of hydrogen at STP is $0.089 k g m^{- 3}$ . Calculate the molar heat capacities $(C_{p} and C_{v})$ of hydrogen.View Solution
Question 33
$4.0 g o f h e l i u m o u π e s 22400 c m^{3}$ at STP. The specific heat capacity of helium at constant pressure is $(5.0 c a l K^{- 1} m o l^{- 1})$ . Calculate the speed of sound in helium at STP.View Solution
Question 34
An ideal gas having density $1.7 \times 10^{- 3} g c m^{- 3} a t a p r e e s u r e$ 1.5 xx 10^(5) $p a i s a f i l \leq d K u n d t t u b e . W h e n t h e g a s i s r e s o \cap a t e d a t a e q u e n c y o f 3.0 k H z, n o d e s a n f or m e d a t a s e p a r a t i o n o f 6.0 c m . C a l c a - - t e t h e h e a t m o l a r h e a t \cap a c i t e s$ (C_p and C_v) of the gas. View Solution
Question 35
Standing waves of frequency $5.0 k H z$ are produced in a tube filled with oxygen at $300 k$ . The separation between the consecutive nodes is $3.3 c m$ . Calculate the specific heat capacities $(C_{p} and C_{v})$ of the gas.View Solution

Home
Ask Doubt
Profile

Exercise from HC VERMA PHYSICS (HINGLISH) SPECIFIC HEAT CAPACITIES OF GASES for Class 11

All Exercises from HC VERMA PHYSICS (HINGLISH) Class 11 PHYSICS SPECIFIC HEAT CAPACITIES OF GASES