Worked Out Examples from HC VERMA PHYSICS Chapter 15 ROTATIONAL MECHANICS for Class 11
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| HC VERMA PHYSICS | Worked Out Examples |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
A wheel of rdius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shownin figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. INitialy, tehwheel is rotating at a speed ω in direction such that the block slides pu the plane. How far wil the block move before stopping?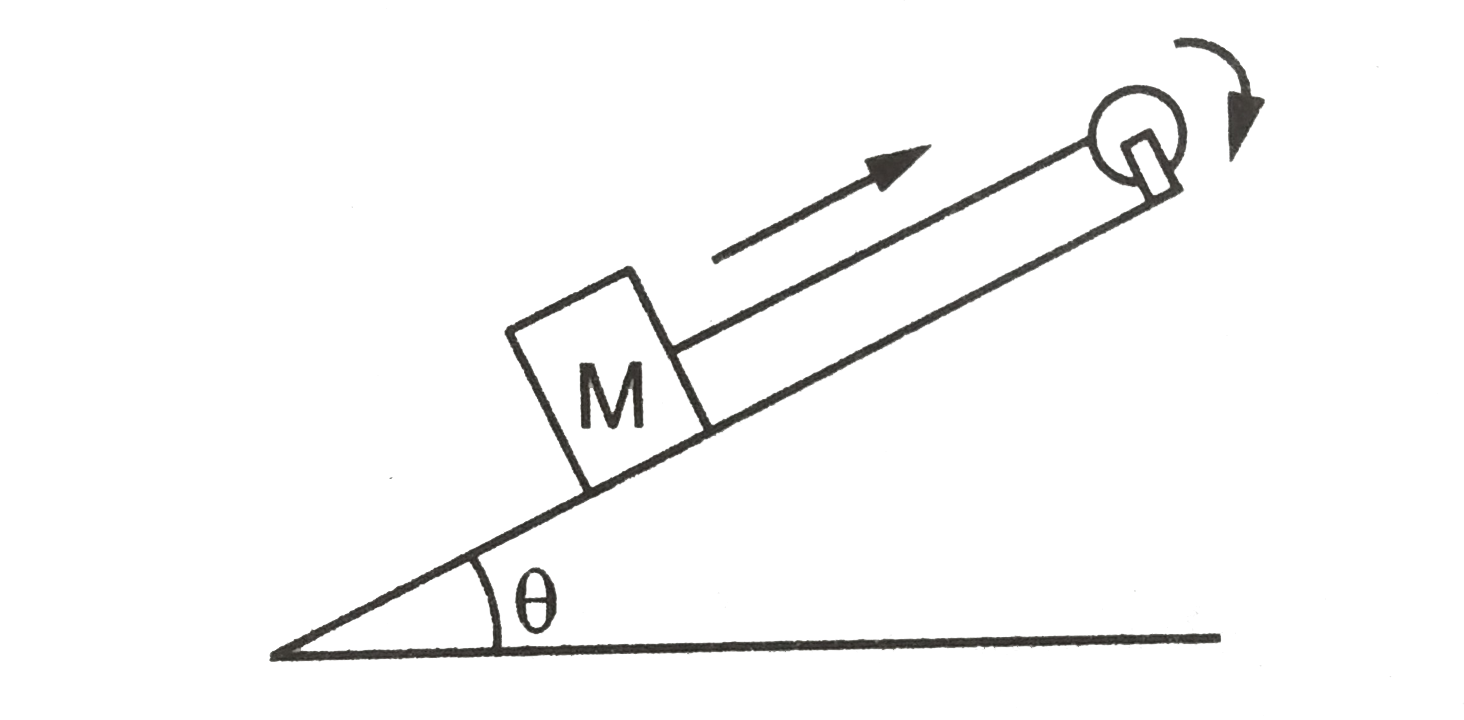 View Solution
View SolutionQuestion 9
The ladder shown in figure has negligible mass and rests on a frictionless floor. The crossbar connects the two legs of the ladder at the middle. The angle between the two legs is 600. The fat person sitting on the ladder has a mas of 80 kg. Find the contact force exerted by the floor on each leg and the tension in the cross bar.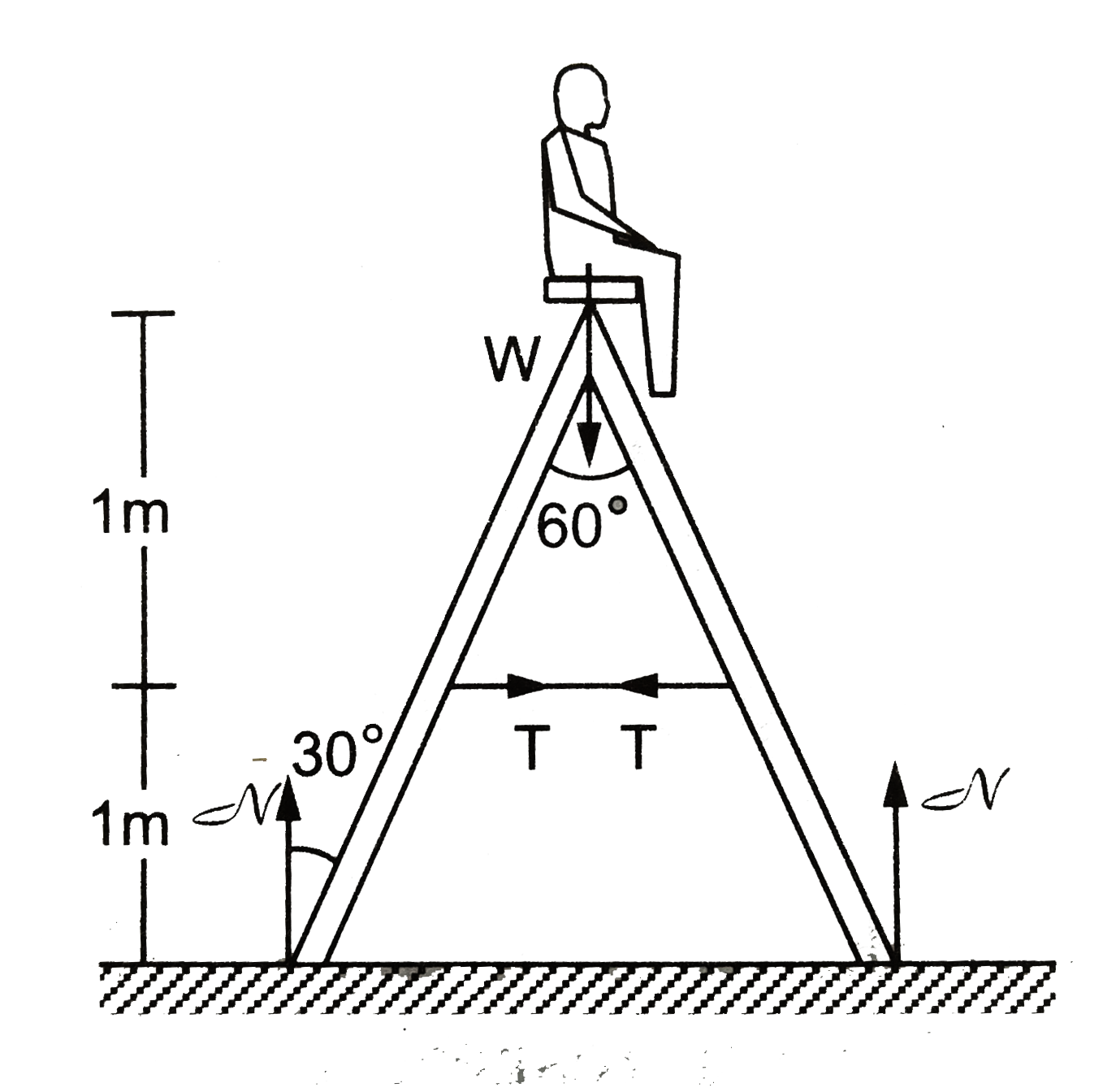 View Solution
View SolutionQuestion 10
Two small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.View SolutionQuestion 11
Two particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centreView SolutionQuestion 15
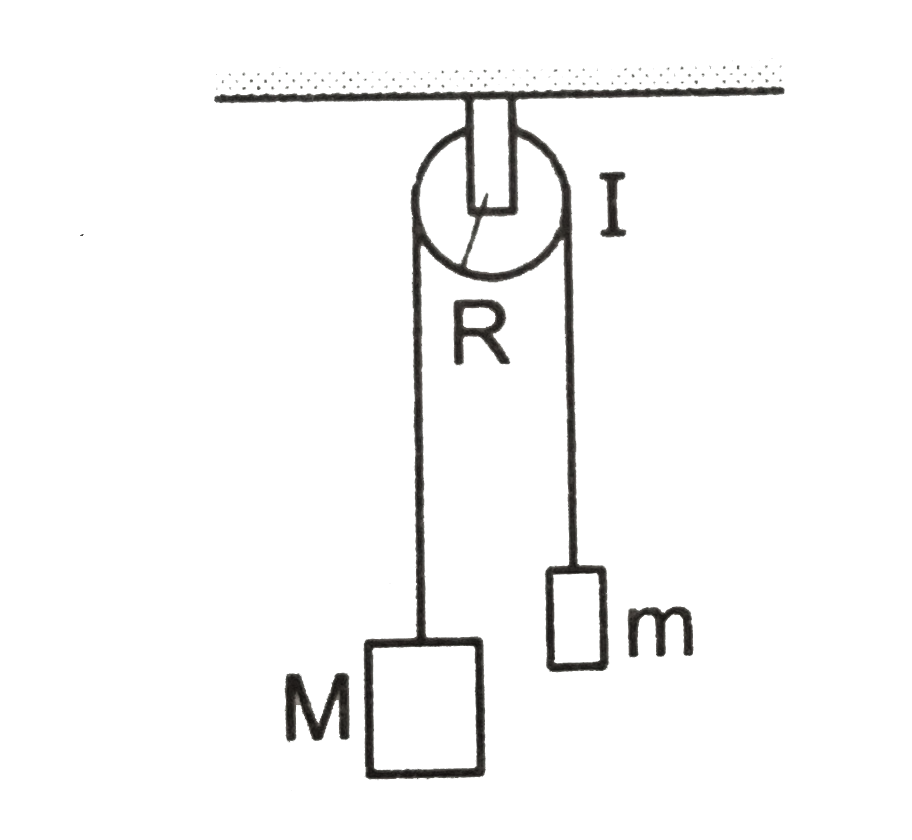
Two masses M and m are connect by a light string gong over a pulley of radis r. The pulley is free to rotate about its axis which is kept horizontal. The moment of inertia of the pulley about the axis is I. The system is releaed from rest. Find the angular momentum fo teh system when teh mass Mhas descended through a height h. The string does not slip over the pulley.View SolutionQuestion 16
Figure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the massView SolutionQuestion 17
A uniform rod of mas m and length l is kept vertical with the lower end clamed. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest positon. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?View SolutionQuestion 21
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision. View SolutionQuestion 25
Figure shows two cylinders of raddi r1andr2 having moments of inertia I1andI2 about their respective axes. Initially the cylinders rotate about their axes with angular speed ω1andω2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slipover each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the sylinders after the slipping ceases. View Solution
View SolutionQuestion 29
The sphere shown in figue lies on a rough plane when a particle of mass m travbelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combine dsystem just after teh collision b. the angular speed of the system about the centre of the sphere just the collistion c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphesre is large compared to teh mass of the partcle so that is large compared toteh mass of the particle so that teh centre of mass of the combined system is not appreciably shifted from the centre of the sphere.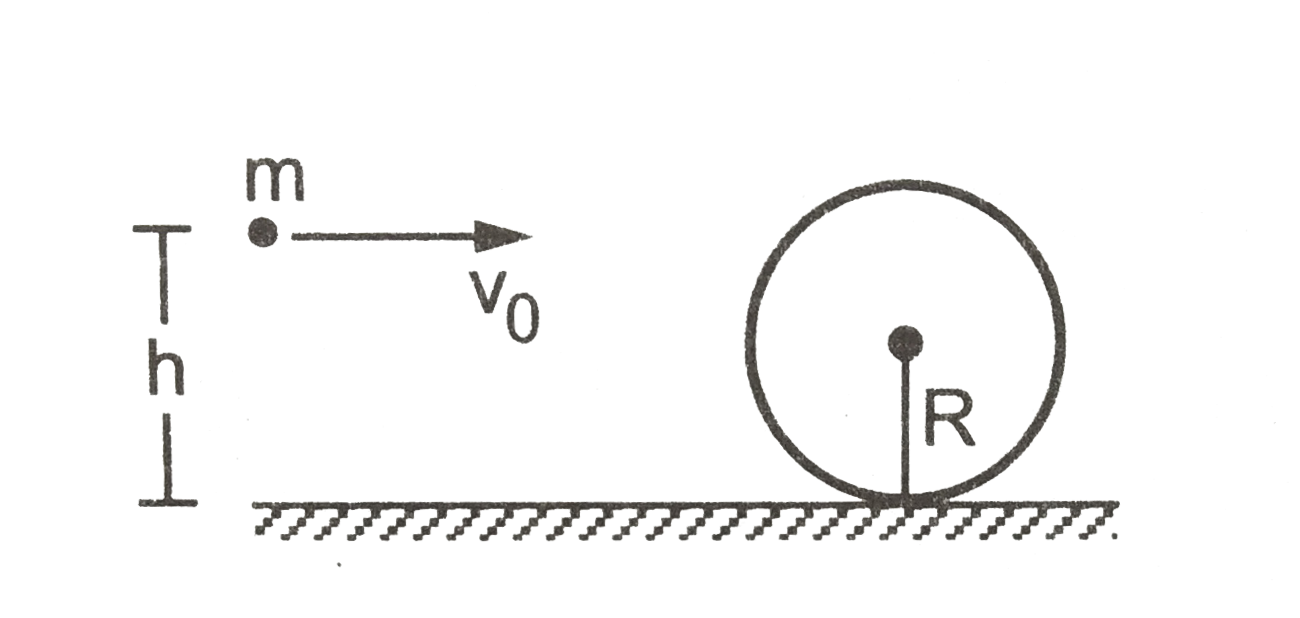 View Solution
View Solution

 .
.