The sphere shown in figue lies on a rough plane when a particle of mass m travbelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combine dsystem just after teh collision b. the angular speed of the system about the centre of the sphere just the collistion c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphesre is large compared to teh mass of the partcle so that is large compared toteh mass of the particle so that teh centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
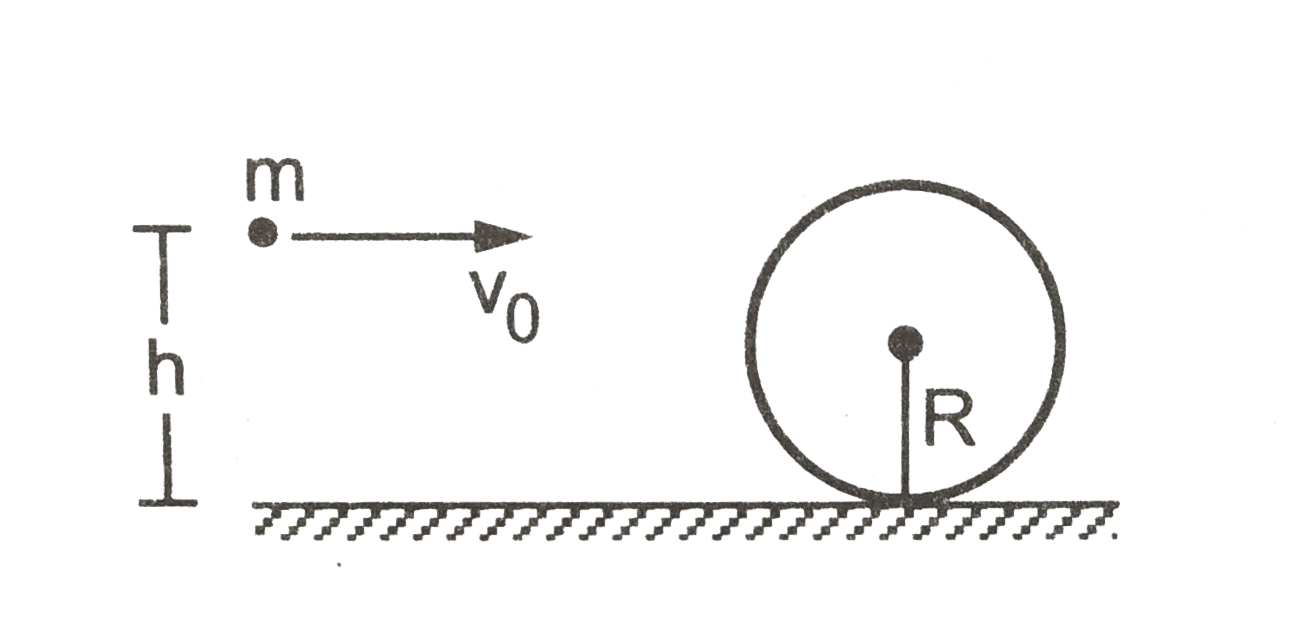
Take the particle plus the sphere as the system
a. Using conservation of linear momentum, the inear speed o the combined system v is given by
mv0=(M+m)vor,v=mv0M+m ……..i
b. Next we shall use conservation angular momentum about the centre of mass, which is to be taken at the centre of the sphere (M>>m) Angular momentum of the particle before collsion is mv0(h−R). If the system rotates with angular speed ω after collision, the angular momentum of the system becomes
(25MR2+mR2)ω
Hence, mv0(h−R)=(25M+m)R2ω
or, ω=mv0(h−R)25M+m⎞⎠R2
c. The sphere will start roling just after the colision if
v=ωRi.e.mv0M+m=mv0(h−R)25M+mR⎞⎠
givingh=⎛⎝75M+2mM+m⎞⎠R=75R.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution
Knowledge Check
A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
Av3B−v3C2v3D−2v3A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)LA particle of mass m moving with speed u collides with the plate of mass m and sticks to it as shown in figure. The recangular place is free to rotae about an axis passing through the centre in horizontal plane. After the collision, the angular velocity of the place will be:
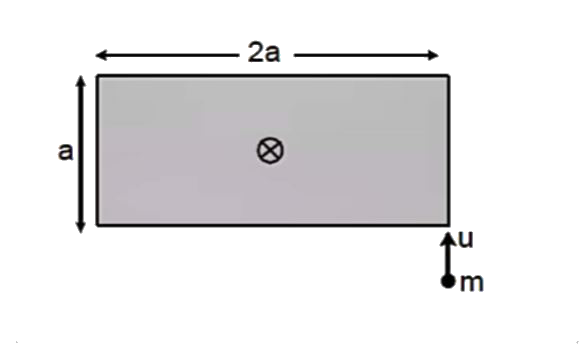 A125uaB1219uaC32uaD35ua
A125uaB1219uaC32uaD35ua
A uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.
View SolutionA uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
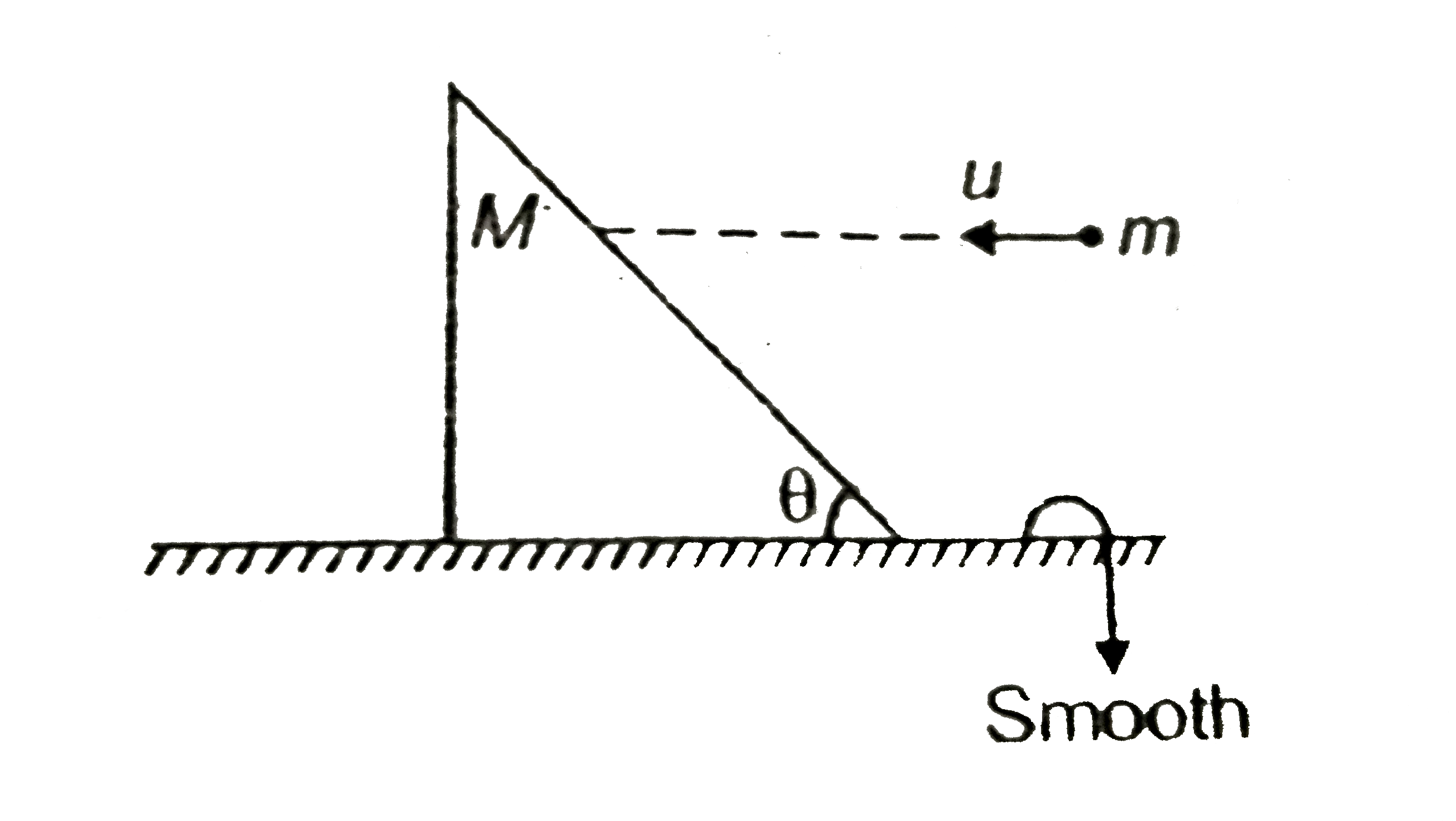
View SolutionA particle of mass m moving with speed u hits a wedge of mass M as shown in figure. If coefficient of restitution is e and friciton can be neglected, then find the speed of the wedge with respect to ground just after the collision.
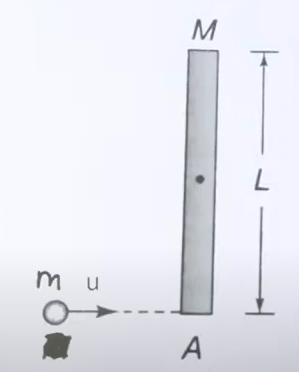
View SolutionA particle of mass m and speed u collides elastically with the end of a uniform rod of mass M and length L as shown. If the particle comes to rest after collision, find mM
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View Solution
