A uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
To solve the problem of finding the normal force and the frictional force that the floor exerts on the ladder, we will follow these steps:
Step 1: Identify the forces acting on the ladder
The forces acting on the ladder include:
- The weight of the ladder (W = mg, where m is the mass and g is the acceleration due to gravity).
- The normal force (N1) exerted by the floor.
- The frictional force (F) exerted by the floor.
- The normal force (N2) exerted by the wall.
Step 2: Calculate the weight of the ladder
Given:
- Mass of the ladder (m) = 10 kg
- Acceleration due to gravity (g) = 9.8 m/s²
The weight (W) of the ladder can be calculated as:
W=mg=10kg×9.8m/s2=98N
Step 3: Set up the equilibrium conditions
Since the ladder is in equilibrium, the sum of the vertical forces and the sum of the horizontal forces must be zero.
1. Vertical Forces:
N1−W=0
N1=W=98N
2. Horizontal Forces:
N2−F=0
N2=F
Step 4: Analyze torques
To find the normal force and frictional force, we will consider torques about the point where the ladder touches the floor (point A). The torque due to the weight of the ladder and the normal force from the wall must balance.
- The distance from the wall to the center of mass of the ladder (which is at L/2) is:
Distance=L2cos(53∘)
- The distance from the wall to the point of contact (point A) is:
Distance=Lsin(53∘)
Setting the torques about point A to be equal:
N2⋅Lsin(53∘)=W⋅(L2cos(53∘))
Step 5: Solve for N2
Substituting W = 98 N into the torque equation:
N2⋅Lsin(53∘)=98⋅(L2cos(53∘))
Cancelling L from both sides (assuming L is not zero):
N2⋅sin(53∘)=49⋅cos(53∘)
N2=49⋅cos(53∘)sin(53∘)
Using the trigonometric values:
- sin(53∘)≈0.8
- cos(53∘)≈0.6
Calculating N2:
N2=49⋅0.60.8=49⋅0.75=36.75N
Step 6: Find the frictional force F
Since N2=F:
F=36.75N
Final Answers:
- Normal force (N1) = 98 N
- Frictional force (F) = 36.75 N
The forces acting on the ladder include:
- The weight of the ladder (W = mg, where m is the mass and g is the acceleration due to gravity).
- The normal force (N1) exerted by the floor.
- The frictional force (F) exerted by the floor.
- The normal force (N2) exerted by the wall.
Given:
- Mass of the ladder (m) = 10 kg
- Acceleration due to gravity (g) = 9.8 m/s²
W=mg=10kg×9.8m/s2=98N
Since the ladder is in equilibrium, the sum of the vertical forces and the sum of the horizontal forces must be zero.
N1−W=0
N1=W=98N
N2−F=0
N2=F
To find the normal force and frictional force, we will consider torques about the point where the ladder touches the floor (point A). The torque due to the weight of the ladder and the normal force from the wall must balance.
Distance=L2cos(53∘)
Distance=Lsin(53∘)
N2⋅Lsin(53∘)=W⋅(L2cos(53∘))
Substituting W = 98 N into the torque equation:
N2⋅Lsin(53∘)=98⋅(L2cos(53∘))
N2⋅sin(53∘)=49⋅cos(53∘)
N2=49⋅cos(53∘)sin(53∘)
- sin(53∘)≈0.8
- cos(53∘)≈0.6
N2=49⋅0.60.8=49⋅0.75=36.75N
Since N2=F:
F=36.75N
- Normal force (N1) = 98 N
- Frictional force (F) = 36.75 N
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
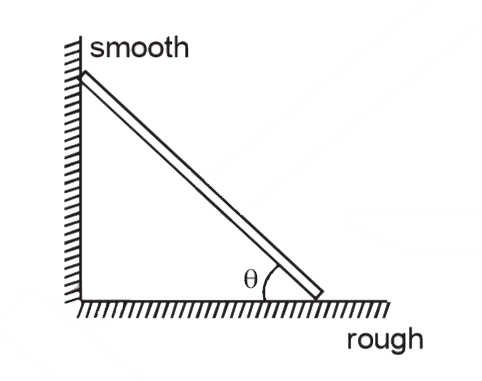
A stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
View SolutionA ladder of mass 20 kg is resting against a vertical smooth wall. Ladder makes an angle 37° with the wall. Other end of the ladder is resting on a rough horizontal floor. Find normal force and force of friction applied on the ladder by horizontal surface.
View Solution
Knowledge Check
A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is
 A50NB50√3NC60√3ND100N
A50NB50√3NC60√3ND100NA ladder 20 ft long is resting angainst a smooth vertical wall at angle of 30∘ with it Its foot lies on a rough ground with coefficient of friction 0⋅3 If the weight of the ladder is 30 kg, then a man of 60 kg weight can climb on the ladder up to the height
A(9√3−5) ftB(9√3+√5)ftC9√3 ftDNone of theseIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of friction between the wall and the ladder is μ1 and that between the floor and the ladder is μ2. the normal reaction of the wall on the ladder is N1 and that of the floor is N2. if the ladder is about to slip. than
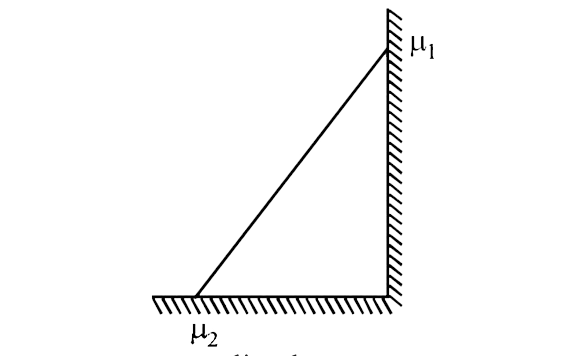 Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
Aμ1=0,μ2≠andN2tanθ=mg2Bμ1≠0,μ2=0andN1tanθ=mg2Cμ1≠0,μ2≠0andN2=mg1+μ1μ2Dμ1=0,μ2≠0andN1tanθ=mg2
A ladder 10m long is leaning against a vertical wall, it makes an angle of 60° with the ground.How far is the foot of the ladder from the wall?
View SolutionA uniform ladder of length L and mass m1 rests against a frictionless wall. The ladder makes an angle θ with the horizontal. (a) Find the horizontal and vertical forces the ground exerts on the base of the ladder when a firefighter of mass m2 is a distance x from the bottom. (b) If the ladder is just on the verge of slipping when the firefighter is a distance d from the bottom, what is the coefficient of static friction between ladder and ground?
View SolutionA uniform ladder of length 10.0 m and mas 16.0 kg is resting against a vertical smooth wall making an angle of 37∘ with it. An electrian weighing 60.0 kg climbs up the ladder. If the stays on the ladder at a point 8.00 m from the lower end, what will be normal force and the force of friction on the ladder by the ground? What should be the minimum coefficient of friction for the electician to work safely?
View SolutionA ladder of mass 10 kg is resting with its top end touching a vertical wall and the bottom end on the floor. If the angle between the ground and the ladder is 45°, find the horizontal force required at the bottom to prevent the ladder from sliding. Neglect friction and take g=10ms−2.
View SolutionA ladder wighing 300 N is placed against a smooth vertical wall having a coefficient of friction between it and the floor of 0.2. What is the maximum force of friction available at the point of contact between the ladder and the floor?
View Solution
