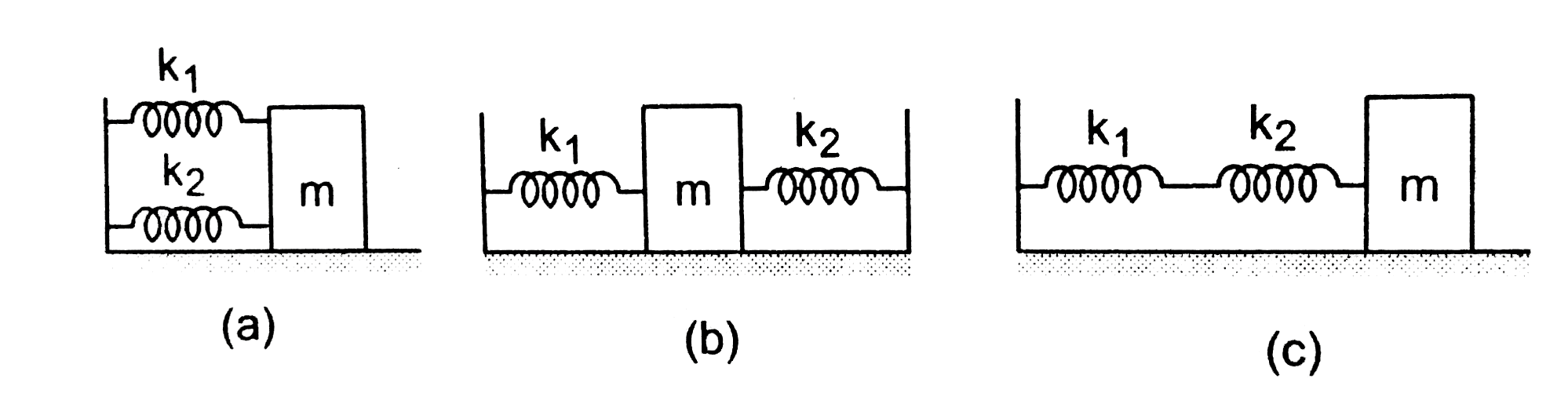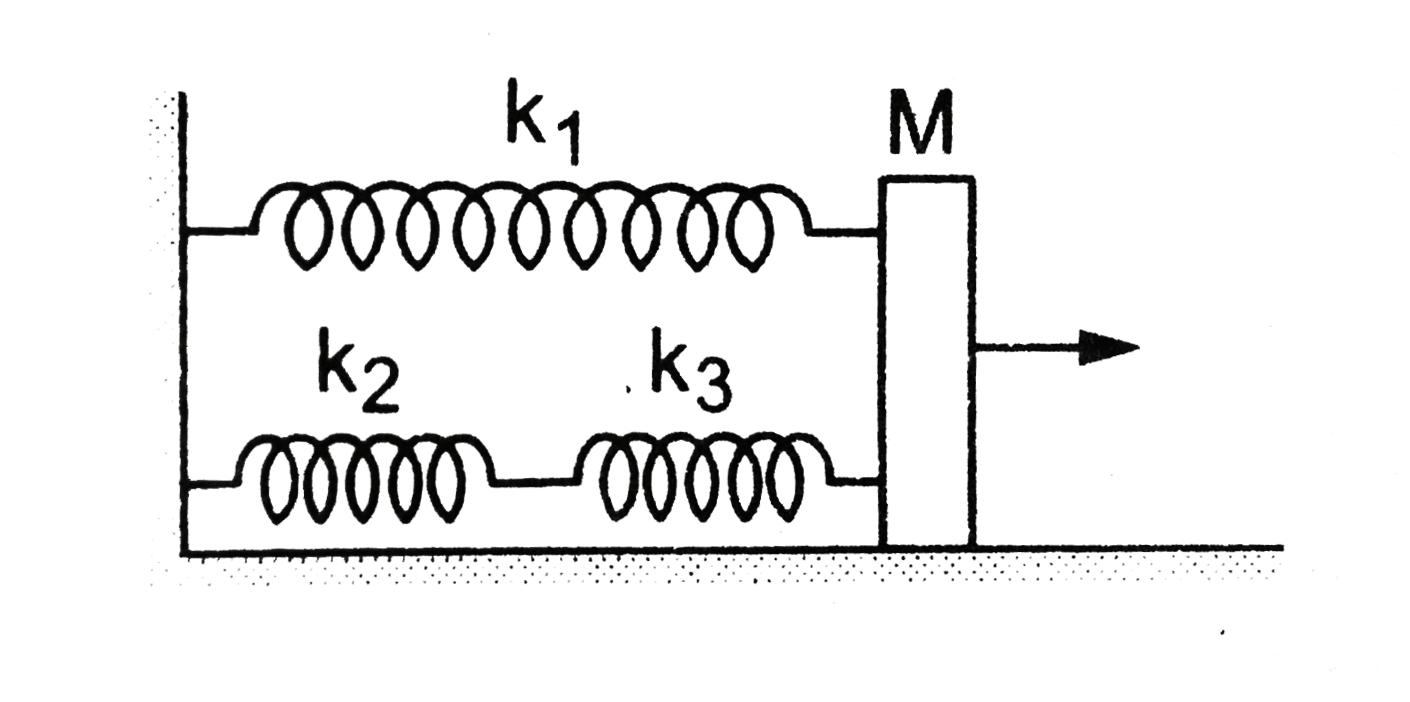Exercises from HC VERMA SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| HC VERMA | Exercises |
| Medium | English |
| Academic Year | 2023-2024 |
Question 7
Consider a particle moving in simple harmonic motion according to the equation
x=2.0cos(50πt+tan−10.75)
where x is in centimetre and t in second. The motion is started at t=0. a. When does the particle come to rest for the first time? B. When does the acceleration have its maximum magnitude for the first time? c. When does the particle comes to rest for the second time?View SolutionQuestion 14
A small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
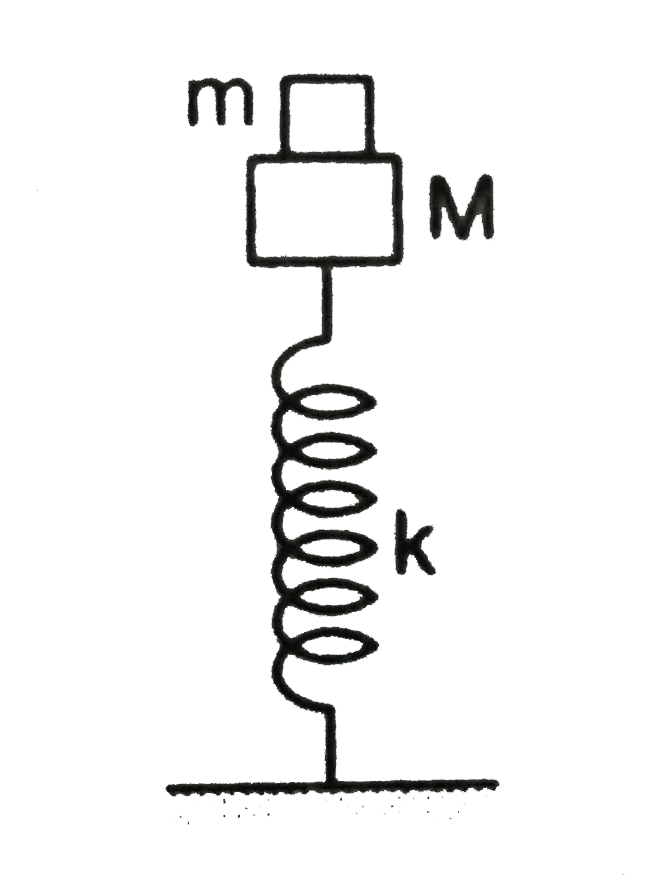 View Solution
View SolutionQuestion 16
In figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
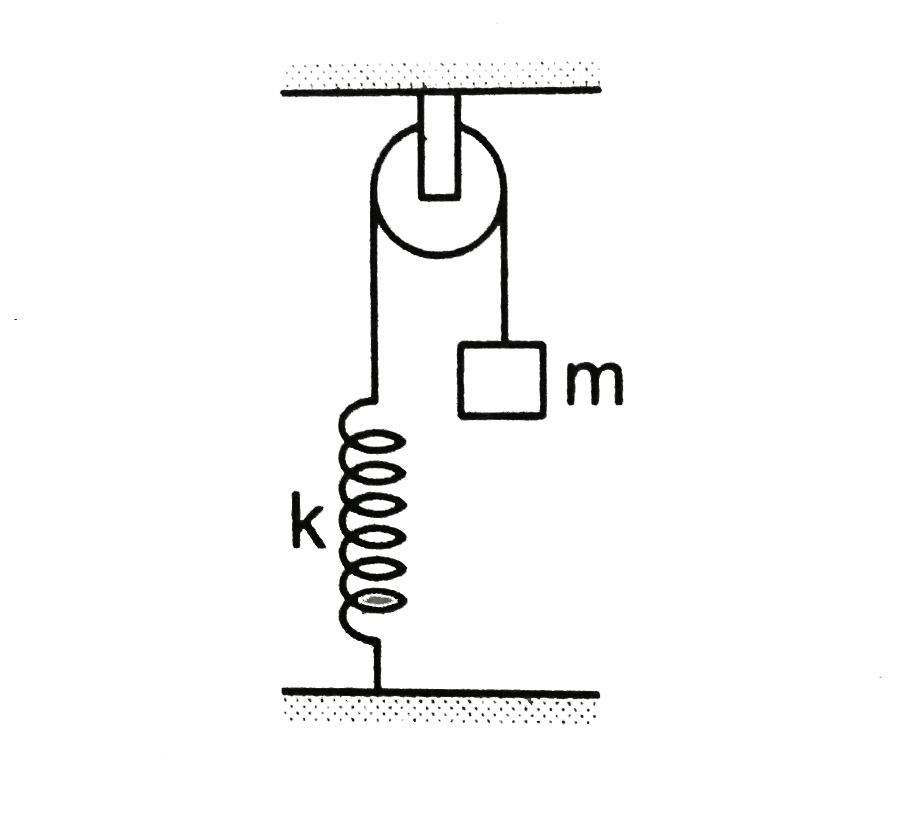
View SolutionQuestion 18
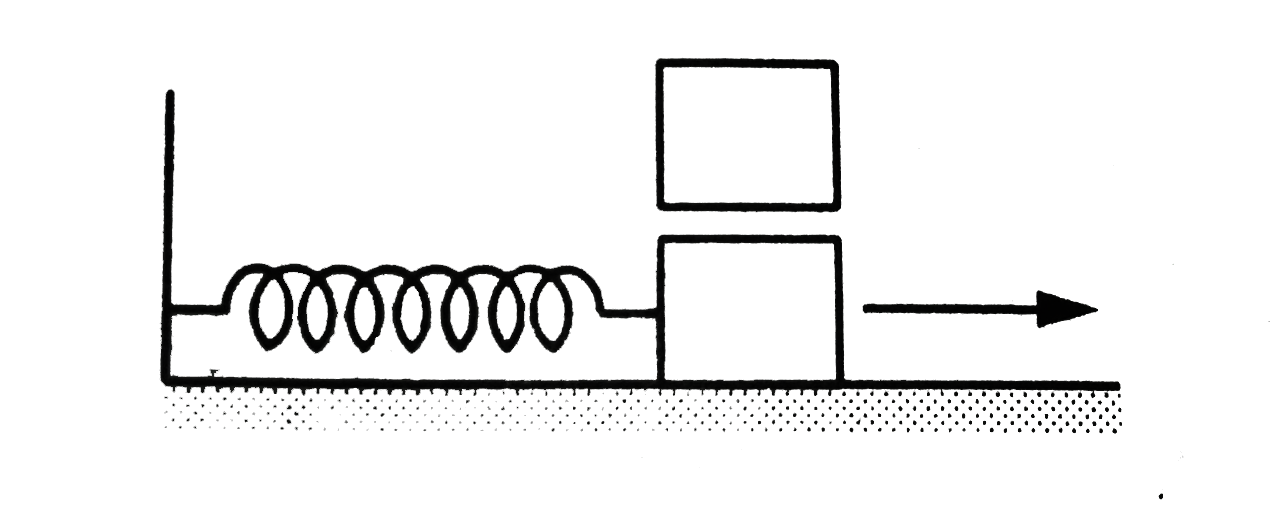
The spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.View SolutionQuestion 26
A rectangular plate of sides a and b is suspended from a ceiling by two parallel strings of length L each in the figure. The separation between the strings is d. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute harmonic motion. Find the time period.
 View Solution
View SolutionQuestion 27
A 1kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring constant 100Nm−1. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency.
 View Solution
View SolutionQuestion 28
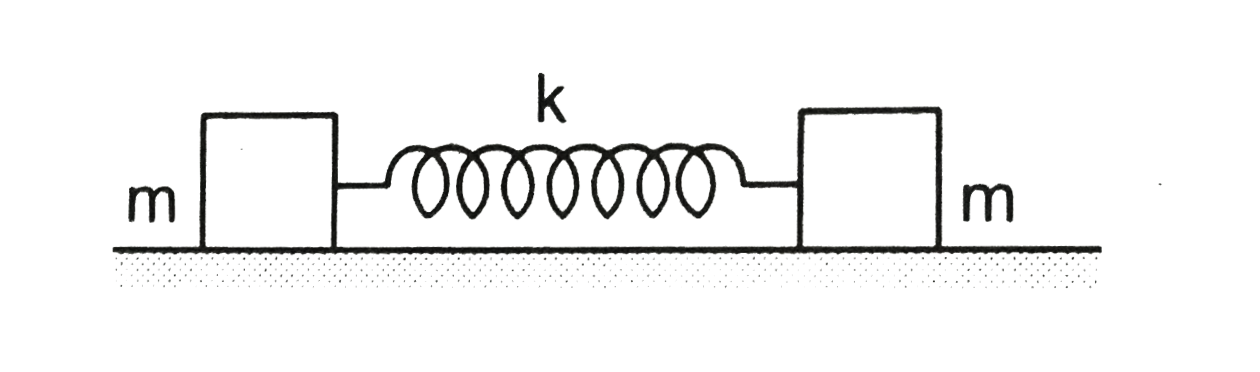
The left block in figure moves at a speed v towards the right block placed in equilibrium. All collisions to take place are elastic and the surfaces are frictionless. Show that motion of the two blocks are periodic. Find the time period of these periodic motions. Neglect the widths of the blocks.
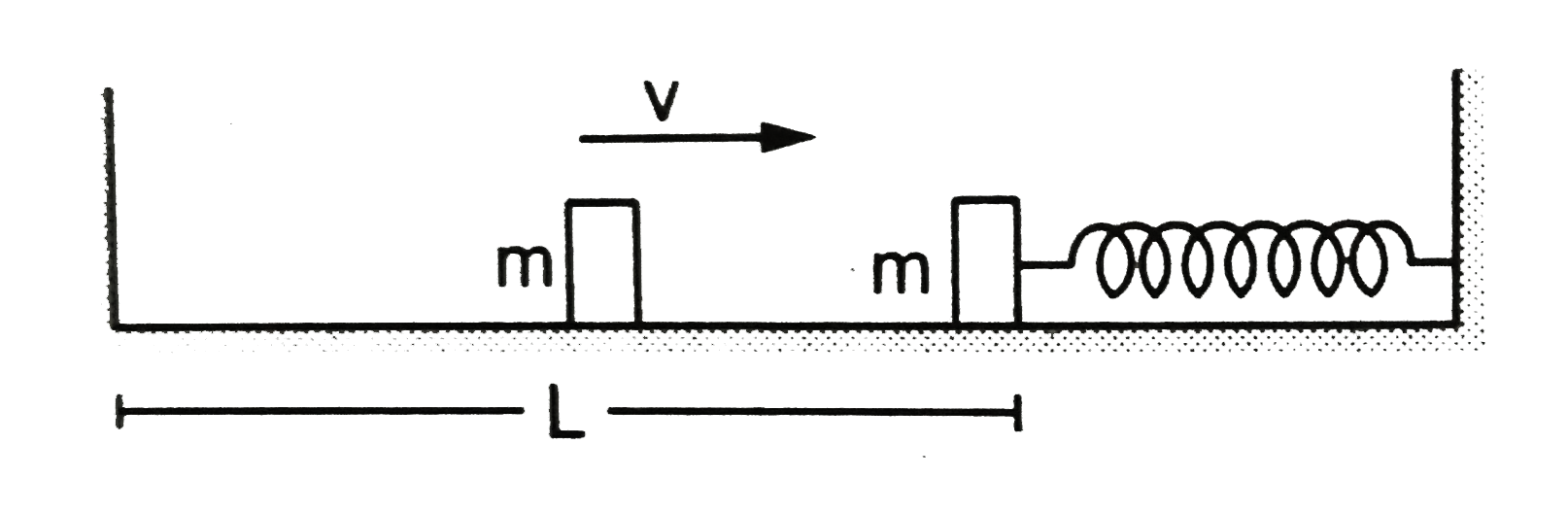 View Solution
View SolutionQuestion 30
All the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is mk and the spring has spring constant. Initialy the car and the block are at rest and the spring is stretched through a length x0 when the system is released. a. Find the amplitude of the simple harmonic motion of the blocks and of the car as seen from the road. b. Find the time periods of the two simple harmonic motions.
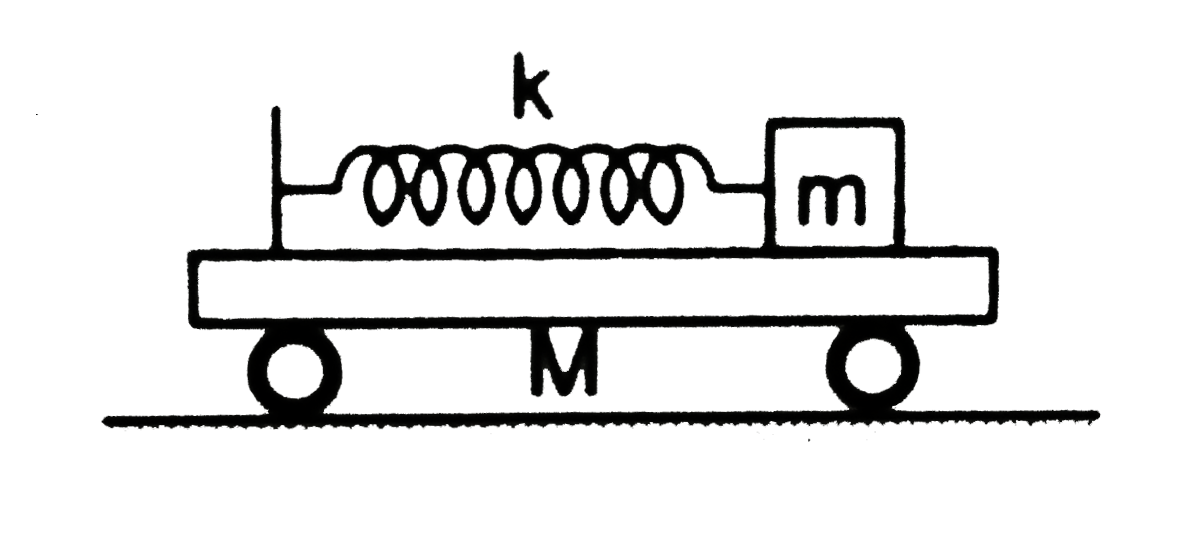 View Solution
View SolutionQuestion 31
A uniform table of mas M stays horizontally and symmetrically on two wheels rotatig in opposite directions figure. The separsation between the wheels is L. The friction coefficeint between each whee, and the plate is μ. Find the time period of oscilationof the pate if it is slightly displaced along its length and released.
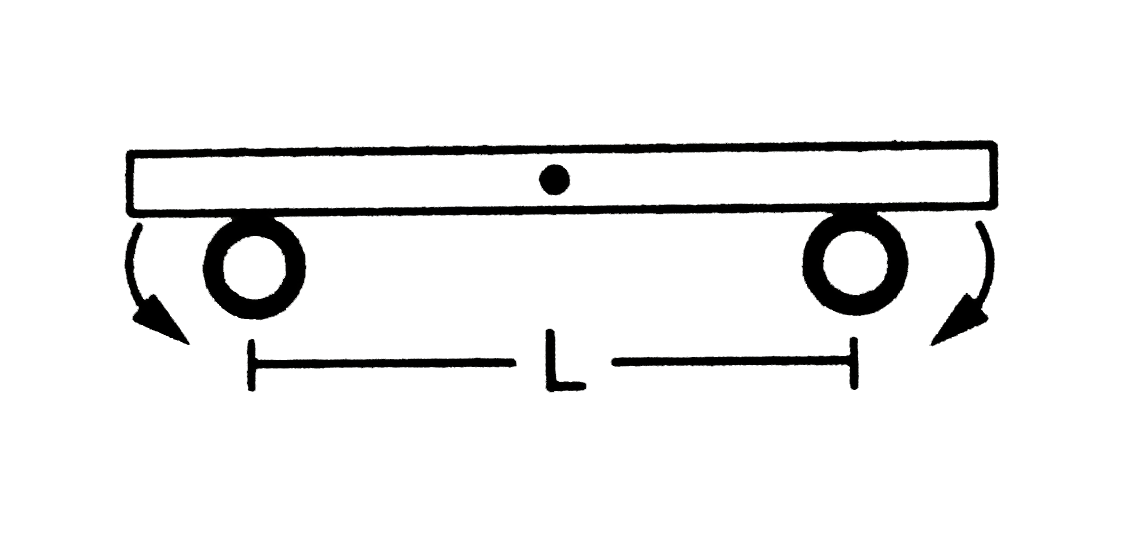 View Solution
View SolutionQuestion 36
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillation. a. How many oscillations does it make per second? b. What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67ms−2?View SolutionQuestion 41
Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.View SolutionQuestion 42
Assume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period. View SolutionQuestion 47
The ear ring of a lady shown in figure has a 3 cm long light suspension wire. A. Find the time period of small oscillations if the lady is standing on the ground. b. The lady now sits in a merry go round moving at 4ms−1 in a circle of radius 2 m. find the time period of small oscillation of the ear ring.
 View Solution
View SolutionQuestion 48
Find the time period of small oscillations of the following system. a. A meter stick suspended through the 20cm mark. b A ring of mas m and radius r suspended through a point on it periphery. c A uniform square plate of edge a suspended through a corner. d. A uniform disc of mass m and radius r suspended through a point r2 away from the center.View SolutionQuestion 52
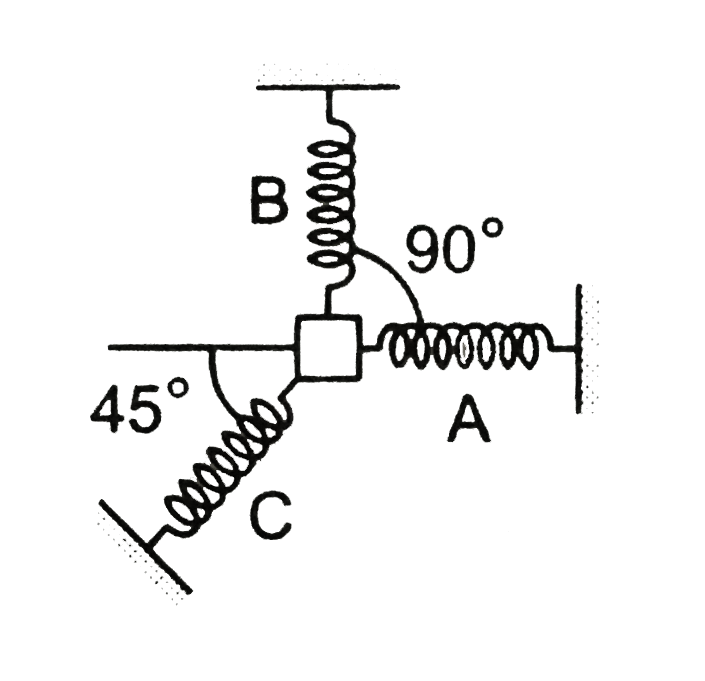
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 2∘ and time period 2s. Find a the radius of the circular wire. b. the speed of the particle farthest away from the point of suspension as it goes though its mean position c. the aceleration of this particle as ilt goes through its mean position and extreme position. Take g=π2sms−2View SolutionQuestion 54
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
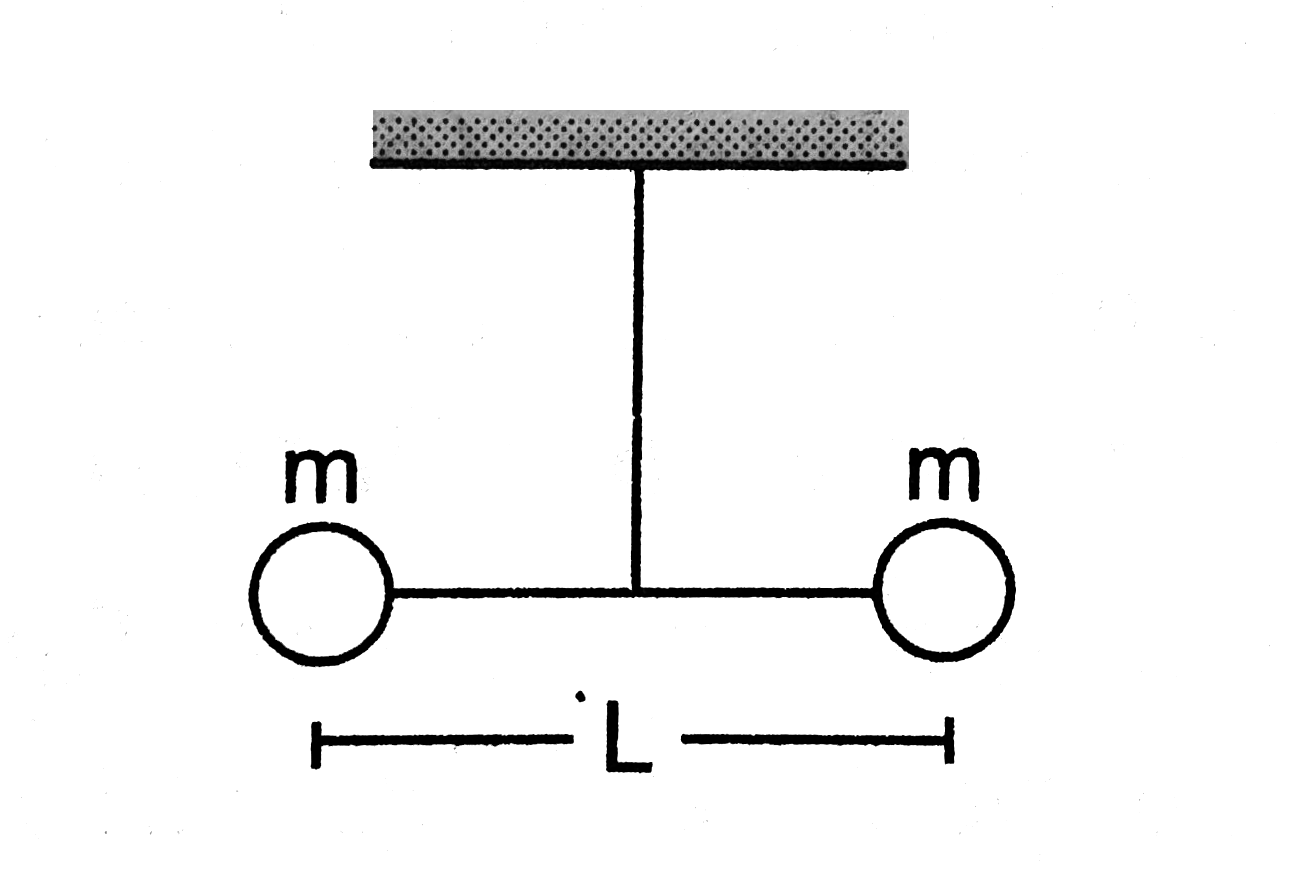 View Solution
View Solution
All Exercises from HC VERMA Class 11 PHYSICS SIMPLE HARMONIC MOTION
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXAMPLES
- EXAMPLES
- EXAMPLE
- EXAMPLES
- EXAMPLES
- EXAMPLE
- EXAMPLES
- EXAMPLES
- EXAMPLE
- OBJECTIVE 1
- OBJECTIVE 1
- OBJECTIVE -1
- OBJECTIVE 1
- OBJECTIVE 1
- OBJECTIVE -1
- OBJECTIVE 1
- OBJECTIVE 1
- OBJECTIVE -1
- OBJECTIVE 2
- OBJECTIVE-2
- OBJECTIVE 2
- OBJECTIVE-2
- OBJECTIVE-2
- OBJECTIVE 2
- OBJECTIVE-2
- OBJECTIVE 2
- OBJECTIVE-2
- OBJECTIVE-2
- OBJECTIVE 2
- OBJECTIVE-2
- OBJECTIVE 2
- OBJECTIVE-2
- OBJECTIVE-2
- QUESTION FOR SHORT ANSWER
- SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- SHORT ANSWER
- QUESTION FOR SHORT ANSWER
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES