HEAT TRANSFER for Class 11 PHYSICS
INTRODUCTION
Jaisa ki aap sabhi ko thoda idea toh hoga hi ki heat aur temperature kya hota hai, jese ki humare pass ek taraf boiling water hai and and dusri taraf ice hai,toh hum jaante hai ki boiling water ka temperature jyada hoga as compare to ice temperature.
Aaj hum iss chapter me jaanege ki heat and temperature hota kya hai,unhe measure kese kr sakte hai hum ,temperature ko measure krne ke liye kon kon si scales use hoti hai and all.
Fir hum iski applications prr bhi baat krenge jese ki body expand kaise ho jaati hai temperature increase hone se.Ek body se dusri body me heat kese transfer krenge, unka state kese change hoga etc.
INTRODUCTION
Jaisa ki aap sabhi ko thoda idea toh hoga hi ki heat aur temperature kya hota hai, jese ki humare pass ek taraf boiling water hai and and dusri taraf ice hai,toh hum jaante hai ki boiling water ka temperature jyada hoga as compare to ice temperature.
Aaj hum iss chapter me jaanege ki heat and temperature hota kya hai,unhe measure kese kr sakte hai hum ,temperature ko measure krne ke liye kon kon si scales use hoti hai and all.
Fir hum iski applications prr bhi baat krenge jese ki body expand kaise ho jaati hai temperature increase hone se.Ek body se dusri body me heat kese transfer krenge, unka state kese change hoga etc.
INTRODUCTION
Jaisa ki aap sabhi ko thoda idea toh hoga hi ki heat aur temperature kya hota hai, jese ki humare pass ek taraf boiling water hai and and dusri taraf ice hai,toh hum jaante hai ki boiling water ka temperature jyada hoga as compare to ice temperature.
Aaj hum iss chapter me jaanege ki heat and temperature hota kya hai,unhe measure kese kr sakte hai hum ,temperature ko measure krne ke liye kon kon si scales use hoti hai and all.
Fir hum iski applications prr bhi baat krenge jese ki body expand kaise ho jaati hai temperature increase hone se.Ek body se dusri body me heat kese transfer krenge, unka state kese change hoga etc.
HEAT TRANSFER
Jesa ki baccho humne heat and temperature me bhi dekha ki heat mtlb hota hai “the way of transfer of energy” mtlb ki heat bhi ek tarah se transfer of energy hota hai.
Aur humne ye bhi dekh rakha hai ki heat ka transfer jab hi hota hai jab do bodies ya system ke beech me temperature difference hota hai,ya phir kisi system ke ek end ka temperature dusre end ke temperature se alag ho,jis se temperature difference aaega or heat transfer ho jaegi.
Ab hum baat krenge ki kitne different tareeko se hum energy transfer kr sakte hai,hum three different tareeko se heat transfer kr sakte hai,voh hai conduction,convection and radiation.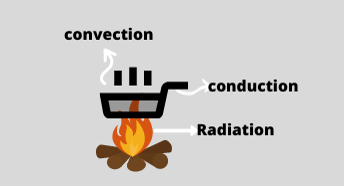
CONDUCTION
Conduction mtlb hai ki kisi body ke do kono prr agr temperature difference hai with each other,toh iss wajah se jo heat transfer hogi isko hum conduction bolenge.Isko hum define krenge“conduction is the mechanism of transfer of heat between two adjacent parts of a body because of their temperature difference.”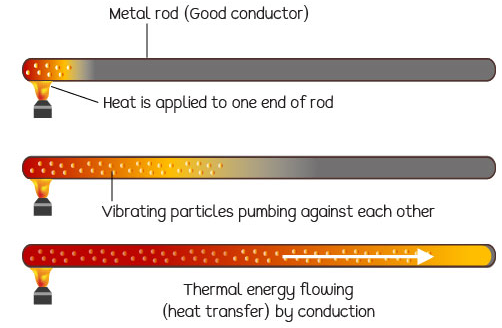
Baccho hum ise ek example se samjhenge ki conduction hota kese hai,
Maan lijiye humne ek mettalic rod li or uss rod ke ek end ko humne heat kiya kisi constant heat source se(maan lijiye 100∘C temperature prr heat kiya), ab hoga ye ki rod ke end ka temperature increase hoga toh uss end ke molecules ki vibrational kinectic energyincrease hogi, ab ye molecule kuch heat absorb krlega or kuch energy apne adjacent molecule ko transfer krdega or ye process chlti rahegi.
Ab ek time esa aaega jab metal ka voh end jaha hum use constant heat provide krwa rhe the,voh heat absorb krna band krdega or jo bhi heat use uss heat source se mil rhi hai voh aage transfer krdega, esa isliye hua baccho kyunki ek state esi aaegi jab iss end ka temperature bhi 100°C ho jaega (jo ki humare source ka temperature hai) ,phir voh heat absorb nhi krega. Ab jese iss end ka temerature fix ho jaega,vese hi poori rod ke har cross section ka temperature constant ho jaega w.r.t time. Iss state ko hum bolte hai steady state.
Maan lijiye ek metallic rod hai jiski length L and coss-section area A hai, and hum baat jab bhi krenge toh steady state ki hi krenge, toh yaha bhi hum assume krenge ki after steady state rod ke ek end a temperature T1 hai and dusre end ka temperature T2 hai.
Toh jo amount of heat flow Q flow hoga in time t voh humne experimentally pta chla ( iska koi proof hai,ise experimentally hi check kiya gya hai)
Heat flow is directly proportional to the cross-section area of that rod,
Q∝A
Heat flow is directly proportional to the temperature difference between the ends of the rod,
Q∝(T1−T2)
Heat flow is directly proportional to the time,
Q∝t
And heat flow is inversly proportional to the length of the rod,
Q∝1L
Jab inn sabo combine krenge toh banega,
Q∝A(T1−T2)tL
Therefore,
Heat flow, Q=KA(T1−T2)tL
Yaha prr k proportionality constant hai jisko hum thermal conductivity of the material bolte hai,
Jitni jyada Kki vale hogi ,utni jyada heat conduct hogi.SI unit of K is Js–1m–1K–1 or Wm–1K–1.
K ki ek common unit bhi hoti hai voh hai calcm−(1)s−1∘C−1.
HEAT CURRENT
Isko hum define krenge “Rate of flow of heat is called heat current”,mtlb heat ek given time me kitna flow kr rhi hai,usko hum bolte hai heat current.
Isko hum ‘H’se denote krte hai.
H=Qt or H=KAT1−T2L
CONVECTION
Convection kevl fluids me possible hota hai,mtlb ki jo deform hone ki ability rakhta hai usme.In convection, “heat is transferred from one place to the other by the actual motion of heated material”, iska mtlb hai baccho ki koi material hai jo ki already heated hai,uss heat ka ek jagah se dusri jagah transfer hona kevl material ke actual motion ki wajah se,use hum kehte hai convention.
Jese ki aapne dekh rakha hoga ki hot air blower hota hai,toh air ko hum heat krte hai air blower ke heating element se or uss heated air ko hum fan se bahar nikalte hai,phir uss hot air se hum dusri cheezo ko heat transfer krte hai, toh iss heat transfer ko humne forcely kiya with the help of heating device, toh ese heat ke transfer ko hum forced convection bolte hai. Or jo jaha hume kisi force ka use nhi krna hota hai ya convection naturally density ke difference ki wajah se hota hai ,use hum natural convection or free convection bote hai.
Natural convection ko hum example se samjhenge, toh gravity important role play krti hai,voh kese,
Jab kisi fluid ko neeche se heat kiya jata hai,toh bottom layer ka temperature increase hoga and voh expand kregi,expand krne se volume increase hoga bottom layer ka and density decrease ho jaegi,aur phir ye bottom layer uss fluid ki topmost layer ko replace krdegi,and ye process chti rahegi,ise hum natural convection bolte hai.
OMR (One Minute Revision)
- * The specific heat capacity of a substance is defined by
s=ΔQmΔT
* Cp = molar specific heat capacity at constant pressure. * Cv = molar specific heat capacity at constant volume. * The SI unit of K (thermal conductivity) is Js–1m–1K–1 or Wm–1K–1.
RADIATION
Radiation bhi ek tareeka hai heat transfer ka,lekin isme hume kisi medium ki jrurat nhi hoti hai jese ki convection and conduction me rehti thi, toh ise hum define kr sakte hai “Heat transfer occurs without any medium or no medium is required to transfer the heat”, mtlb bina medium ka use kiye hum heat ko transfer krte hai use hum radiation kehte hai.Iska simple sa example lete hai hum,jese ki earth and sun ke beech me bhut distance hai,phir bhi sun se heat earth tk aajati hai,sun se jo heat earth tk aati hai voh bina kisi medium ki help se aati hai,iska mtlb hua ki earth prr heat radiation ki wajah se aati hai aur voh electro magnetic wave ke form me aati hai.
Ab radiation kese hoga isme kya hoga,ye sab hum pta krenge,toh baccho iski ek theory di gyi,
PREVOST THEORY OF EXCHANGE
Prevost ne kaha ki “ all bodies emits thermal radiation at all temperature” and “all bodies absorbs thermal/heat radiations falling on it at all temperature”,mtlb hai baccho ki prevost ne kaha ki duniya ki saari bodies jese pen,paper,human body vagerah vagerah ,ye sab heat radiate bhi krti hai and absorb bhi krti hai har temperature prr.Ab konsi boy kitni heat radiate krti hai ya absorb krti hai ye uss body ke material and temperature prr depend krega,that is “ amount of heat emitted/absorbed is depend upon temperature and material of the body”.
Maan lijiye ki surrounding ka temperature body ke temperature se jyada hai, iska mtlb body heat absorb jyada kregi as compare to emission and agr surrounding ka temperature body ke temperature se kam hai,toh iska mtlb body heat emit jyada kregi as compare ki absorbtion. Ab inn dono condition me ek time esa aaega ki dono surrounding and body thermal equilibrium me aajaenge (dono ka temperature same ho jaega),uss time voh body jitna heat absorb kregi utni hi heat emit bhi kregi, “amount of heat absorbed = amount of heat emitted”.
BLACK BODY RADIATION
Agr definition ki baat krein toh bolenge “ Body which absorb all radiations falling on it at any temperature at any incident angle” mtlb hai ki esi body jo saare radiation ko absorb krle jo bhi uske upar aa rhe hai ,kisi bhi temperature prr and kisi bhi angle se. Black body zero reflection deti hai,mtlb ki jitni radiation uske upar aaegi voh poori ki poori absorb krlegi and kuch bhi radiation ko vaps reflect nhi kregi and black body zero transmittence bhi show krta hai ,mtlb ki uss body se koi bhi radiation bahar nhi jaati hai,sab ki sab absorb ho jaati hai.Baccho iska naam black body isliye rakha gya kyunki hum sabko pta hai ki black colour bhut accha absorber hota hai (black colour is a good absorber),yhi dekhte hue iska naam blac body radiation rakha gya,mtlb hai ki jo body bhut acchi absorber hoti hai or poori ki poori radiation ko absorb krleta hai.Ab iska mtlb ye nhi hai ki body black colou ki hi hogi,voh kisi bhi colour ki ho sakti hai jese red,blue,green,orange anything.
WIENS DISPLACEMENT LAW
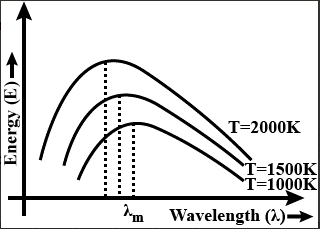
Baccho jesa ki aap upar dekh rhe honge ki intensity vs wavelength ka graph diya hua hai,toh phle hum isko samjhenge ki ye hai kya,
Jesa ki aap sabhi jaante hai ki kisi bhi body ko hum heat krte hai toh different different wavelengths waali intensity nikalti hai (radiation ka mtlb hi hota hai ki electromagnetic wave ki through heat transfer hona and waves ki wavelengths toh hoti hi hai).
Toh humne ek experiment kiya or kisi ek body ko kisi temerature prr heat kiya( maan lijiye voh temperature hai T1) , toh dekha gya ki multiple wavelength ki radiations nikli,or usme se sabse jyada radiation jis wavelength ki nikli use humne λmax1 se denote kiya,or ye same process humne different different temperatures prr perfore kari toh dekha ki T2 prr wavelength λmax2 hai and T3 prr wavelength λmax3 hai.
Hum temperature ko iss form me rakha , T3>T2>T1 toh hume ta chla ki wavelength λmax1>λmax2>λmax3 aai.
Mtlb jese jese temperature increase krte jaenge vese vese sabse jyada radiation emit krne waali wavelength decrease hoti jaegi,
Ab wiens ne kya dekha ki jab λmax and T ka hum product krte hai for any value of temperature, voh humesha constant aai
. That means ,
λmaxT = constant
Ye relation wiens ne dekha tha isliye ise wiens displacement law bolte hai.
The value of the constant (Wien’s constant) is 2.9×10–3mK .
STEFAN-BOLTZMANN LAW
Ye law hume btata hai ki for a perfectly black body,
Intensity of radiation is directiy proportional to the fourth power of temperature,
QAt∝T4
QAt=σ(T4)
Now, Q/t = sigmaA(T^4)<b>,<br>Andthiswecansay,thee≠rgyemiedperunittimeis≺br><b>H = sigmaA(T^4)<b>,thisisstefans−bo<zma∩lawforperfectlyblackbodyandtheconstantsigmaiscal≤dStefan−Bo<zma∩constant.Itsvalue∈SIunitsis<b>5.67 × 10–8 W m^(–2) K^(–4) <b><br>AndagrkoibodykatemperatureThaiorsurround∈gskatemperatureTshai,→hjoe≠rgyperunittimeradiatehogiusehumlikhen≥,<b>H = sigmaA(T^4-T^s)<b>,<br>Agrkisibodykiemissivity<b>e<b>hai→hmodifiykrkehumlikhen≥,<br><b>H = sigmaeA(T^4-T^s)<b><br>Where<b>0<=e<=1
HEAT TRANSFER
Jesa ki baccho humne heat and temperature me bhi dekha ki heat mtlb hota hai “the way of transfer of energy” mtlb ki heat bhi ek tarah se transfer of energy hota hai.
Aur humne ye bhi dekh rakha hai ki heat ka transfer jab hi hota hai jab do bodies ya system ke beech me temperature difference hota hai,ya phir kisi system ke ek end ka temperature dusre end ke temperature se alag ho,jis se temperature difference aaega or heat transfer ho jaegi.
Ab hum baat krenge ki kitne different tareeko se hum energy transfer kr sakte hai,hum three different tareeko se heat transfer kr sakte hai,voh hai conduction,convection and radiation.
CONDUCTION
Conduction mtlb hai ki kisi body ke do kono prr agr temperature difference hai with each other,toh iss wajah se jo heat transfer hogi isko hum conduction bolenge.Isko hum define krenge“conduction is the mechanism of transfer of heat between two adjacent parts of a body because of their temperature difference.”
Baccho hum ise ek example se samjhenge ki conduction hota kese hai,
Maan lijiye humne ek mettalic rod li or uss rod ke ek end ko humne heat kiya kisi constant heat source se(maan lijiye 100∘C temperature prr heat kiya), ab hoga ye ki rod ke end ka temperature increase hoga toh uss end ke molecules ki vibrational kinectic energyincrease hogi, ab ye molecule kuch heat absorb krlega or kuch energy apne adjacent molecule ko transfer krdega or ye process chlti rahegi.
Ab ek time esa aaega jab metal ka voh end jaha hum use constant heat provide krwa rhe the,voh heat absorb krna band krdega or jo bhi heat use uss heat source se mil rhi hai voh aage transfer krdega, esa isliye hua baccho kyunki ek state esi aaegi jab iss end ka temperature bhi 100°C ho jaega (jo ki humare source ka temperature hai) ,phir voh heat absorb nhi krega. Ab jese iss end ka temerature fix ho jaega,vese hi poori rod ke har cross section ka temperature constant ho jaega w.r.t time. Iss state ko hum bolte hai steady state.
Maan lijiye ek metallic rod hai jiski length L and coss-section area A hai, and hum baat jab bhi krenge toh steady state ki hi krenge, toh yaha bhi hum assume krenge ki after steady state rod ke ek end a temperature T1 hai and dusre end ka temperature T2 hai.
Toh jo amount of heat flow Q flow hoga in time t voh humne experimentally pta chla ( iska koi proof hai,ise experimentally hi check kiya gya hai)
Heat flow is directly proportional to the cross-section area of that rod,
Q∝A
Heat flow is directly proportional to the temperature difference between the ends of the rod,
Q∝(T1−T2)
Heat flow is directly proportional to the time,
Q∝t
And heat flow is inversly proportional to the length of the rod,
Q∝1L
Jab inn sabo combine krenge toh banega,
Q∝A(T1−T2)tL
Therefore,
Heat flow, Q=KA(T1−T2)tL
Yaha prr k proportionality constant hai jisko hum thermal conductivity of the material bolte hai,
Jitni jyada Kki vale hogi ,utni jyada heat conduct hogi.SI unit of K is Js–1m–1K–1 or Wm–1K–1.
K ki ek common unit bhi hoti hai voh hai calcm−(1)s−1∘C−1.
HEAT CURRENT
Isko hum define krenge “Rate of flow of heat is called heat current”,mtlb heat ek given time me kitna flow kr rhi hai,usko hum bolte hai heat current.
Isko hum ‘H’se denote krte hai.
H=Qt or H=KAT1−T2L
CONVECTION
Convection kevl fluids me possible hota hai,mtlb ki jo deform hone ki ability rakhta hai usme.In convection, “heat is transferred from one place to the other by the actual motion of heated material”, iska mtlb hai baccho ki koi material hai jo ki already heated hai,uss heat ka ek jagah se dusri jagah transfer hona kevl material ke actual motion ki wajah se,use hum kehte hai convention.
Jese ki aapne dekh rakha hoga ki hot air blower hota hai,toh air ko hum heat krte hai air blower ke heating element se or uss heated air ko hum fan se bahar nikalte hai,phir uss hot air se hum dusri cheezo ko heat transfer krte hai, toh iss heat transfer ko humne forcely kiya with the help of heating device, toh ese heat ke transfer ko hum forced convection bolte hai. Or jo jaha hume kisi force ka use nhi krna hota hai ya convection naturally density ke difference ki wajah se hota hai ,use hum natural convection or free convection bote hai.
Natural convection ko hum example se samjhenge, toh gravity important role play krti hai,voh kese,
Jab kisi fluid ko neeche se heat kiya jata hai,toh bottom layer ka temperature increase hoga and voh expand kregi,expand krne se volume increase hoga bottom layer ka and density decrease ho jaegi,aur phir ye bottom layer uss fluid ki topmost layer ko replace krdegi,and ye process chti rahegi,ise hum natural convection bolte hai.
OMR (One Minute Revision)
- * The specific heat capacity of a substance is defined by
s=ΔQmΔT
* Cp = molar specific heat capacity at constant pressure. * Cv = molar specific heat capacity at constant volume. * The SI unit of K (thermal conductivity) is Js–1m–1K–1 or Wm–1K–1.
RADIATION
Radiation bhi ek tareeka hai heat transfer ka,lekin isme hume kisi medium ki jrurat nhi hoti hai jese ki convection and conduction me rehti thi, toh ise hum define kr sakte hai “Heat transfer occurs without any medium or no medium is required to transfer the heat”, mtlb bina medium ka use kiye hum heat ko transfer krte hai use hum radiation kehte hai.Iska simple sa example lete hai hum,jese ki earth and sun ke beech me bhut distance hai,phir bhi sun se heat earth tk aajati hai,sun se jo heat earth tk aati hai voh bina kisi medium ki help se aati hai,iska mtlb hua ki earth prr heat radiation ki wajah se aati hai aur voh electro magnetic wave ke form me aati hai.
Ab radiation kese hoga isme kya hoga,ye sab hum pta krenge,toh baccho iski ek theory di gyi,
PREVOST THEORY OF EXCHANGE
Prevost ne kaha ki “ all bodies emits thermal radiation at all temperature” and “all bodies absorbs thermal/heat radiations falling on it at all temperature”,mtlb hai baccho ki prevost ne kaha ki duniya ki saari bodies jese pen,paper,human body vagerah vagerah ,ye sab heat radiate bhi krti hai and absorb bhi krti hai har temperature prr.Ab konsi boy kitni heat radiate krti hai ya absorb krti hai ye uss body ke material and temperature prr depend krega,that is “ amount of heat emitted/absorbed is depend upon temperature and material of the body”.
Maan lijiye ki surrounding ka temperature body ke temperature se jyada hai, iska mtlb body heat absorb jyada kregi as compare to emission and agr surrounding ka temperature body ke temperature se kam hai,toh iska mtlb body heat emit jyada kregi as compare ki absorbtion. Ab inn dono condition me ek time esa aaega ki dono surrounding and body thermal equilibrium me aajaenge (dono ka temperature same ho jaega),uss time voh body jitna heat absorb kregi utni hi heat emit bhi kregi, “amount of heat absorbed = amount of heat emitted”.
BLACK BODY RADIATION
Agr definition ki baat krein toh bolenge “ Body which absorb all radiations falling on it at any temperature at any incident angle” mtlb hai ki esi body jo saare radiation ko absorb krle jo bhi uske upar aa rhe hai ,kisi bhi temperature prr and kisi bhi angle se. Black body zero reflection deti hai,mtlb ki jitni radiation uske upar aaegi voh poori ki poori absorb krlegi and kuch bhi radiation ko vaps reflect nhi kregi and black body zero transmittence bhi show krta hai ,mtlb ki uss body se koi bhi radiation bahar nhi jaati hai,sab ki sab absorb ho jaati hai.Baccho iska naam black body isliye rakha gya kyunki hum sabko pta hai ki black colour bhut accha absorber hota hai (black colour is a good absorber),yhi dekhte hue iska naam blac body radiation rakha gya,mtlb hai ki jo body bhut acchi absorber hoti hai or poori ki poori radiation ko absorb krleta hai.Ab iska mtlb ye nhi hai ki body black colou ki hi hogi,voh kisi bhi colour ki ho sakti hai jese red,blue,green,orange anything.
WIENS DISPLACEMENT LAW

Baccho jesa ki aap upar dekh rhe honge ki intensity vs wavelength ka graph diya hua hai,toh phle hum isko samjhenge ki ye hai kya,
Jesa ki aap sabhi jaante hai ki kisi bhi body ko hum heat krte hai toh different different wavelengths waali intensity nikalti hai (radiation ka mtlb hi hota hai ki electromagnetic wave ki through heat transfer hona and waves ki wavelengths toh hoti hi hai).
Toh humne ek experiment kiya or kisi ek body ko kisi temerature prr heat kiya( maan lijiye voh temperature hai T1) , toh dekha gya ki multiple wavelength ki radiations nikli,or usme se sabse jyada radiation jis wavelength ki nikli use humne λmax1 se denote kiya,or ye same process humne different different temperatures prr perfore kari toh dekha ki T2 prr wavelength λmax2 hai and T3 prr wavelength λmax3 hai.
Hum temperature ko iss form me rakha , T3>T2>T1 toh hume ta chla ki wavelength λmax1>λmax2>λmax3 aai.
Mtlb jese jese temperature increase krte jaenge vese vese sabse jyada radiation emit krne waali wavelength decrease hoti jaegi,
Ab wiens ne kya dekha ki jab λmax and T ka hum product krte hai for any value of temperature, voh humesha constant aai
. That means ,
λmaxT = constant
Ye relation wiens ne dekha tha isliye ise wiens displacement law bolte hai.
The value of the constant (Wien’s constant) is 2.9×10–3mK .
STEFAN-BOLTZMANN LAW
Ye law hume btata hai ki for a perfectly black body,
Intensity of radiation is directiy proportional to the fourth power of temperature,
QAt∝T4
QAt=σ(T4)
Now, Q/t = sigmaA(T^4)<b>,<br>Andthiswecansay,thee≠rgyemiedperunittimeis≺br><b>H = sigmaA(T^4)<b>,thisisstefans−bo<zma∩lawforperfectlyblackbodyandtheconstantsigmaiscal≤dStefan−Bo<zma∩constant.Itsvalue∈SIunitsis<b>5.67 × 10–8 W m^(–2) K^(–4) <b><br>AndagrkoibodykatemperatureThaiorsurround∈gskatemperatureTshai,→hjoe≠rgyperunittimeradiatehogiusehumlikhen≥,<b>H = sigmaA(T^4-T^s)<b>,<br>Agrkisibodykiemissivity<b>e<b>hai→hmodifiykrkehumlikhen≥,<br><b>H = sigmaeA(T^4-T^s)<b><br>Where<b>0<=e<=1
HEAT TRANSFER
Jesa ki baccho humne heat and temperature me bhi dekha ki heat mtlb hota hai “the way of transfer of energy” mtlb ki heat bhi ek tarah se transfer of energy hota hai.
Aur humne ye bhi dekh rakha hai ki heat ka transfer jab hi hota hai jab do bodies ya system ke beech me temperature difference hota hai,ya phir kisi system ke ek end ka temperature dusre end ke temperature se alag ho,jis se temperature difference aaega or heat transfer ho jaegi.
Ab hum baat krenge ki kitne different tareeko se hum energy transfer kr sakte hai,hum three different tareeko se heat transfer kr sakte hai,voh hai conduction,convection and radiation.
CONDUCTION
Conduction mtlb hai ki kisi body ke do kono prr agr temperature difference hai with each other,toh iss wajah se jo heat transfer hogi isko hum conduction bolenge.Isko hum define krenge“conduction is the mechanism of transfer of heat between two adjacent parts of a body because of their temperature difference.”
Baccho hum ise ek example se samjhenge ki conduction hota kese hai,
Maan lijiye humne ek mettalic rod li or uss rod ke ek end ko humne heat kiya kisi constant heat source se(maan lijiye 100∘C temperature prr heat kiya), ab hoga ye ki rod ke end ka temperature increase hoga toh uss end ke molecules ki vibrational kinectic energyincrease hogi, ab ye molecule kuch heat absorb krlega or kuch energy apne adjacent molecule ko transfer krdega or ye process chlti rahegi.
Ab ek time esa aaega jab metal ka voh end jaha hum use constant heat provide krwa rhe the,voh heat absorb krna band krdega or jo bhi heat use uss heat source se mil rhi hai voh aage transfer krdega, esa isliye hua baccho kyunki ek state esi aaegi jab iss end ka temperature bhi 100°C ho jaega (jo ki humare source ka temperature hai) ,phir voh heat absorb nhi krega. Ab jese iss end ka temerature fix ho jaega,vese hi poori rod ke har cross section ka temperature constant ho jaega w.r.t time. Iss state ko hum bolte hai steady state.
Maan lijiye ek metallic rod hai jiski length L and coss-section area A hai, and hum baat jab bhi krenge toh steady state ki hi krenge, toh yaha bhi hum assume krenge ki after steady state rod ke ek end a temperature T1 hai and dusre end ka temperature T2 hai.
Toh jo amount of heat flow Q flow hoga in time t voh humne experimentally pta chla ( iska koi proof hai,ise experimentally hi check kiya gya hai)
Heat flow is directly proportional to the cross-section area of that rod,
Q∝A
Heat flow is directly proportional to the temperature difference between the ends of the rod,
Q∝(T1−T2)
Heat flow is directly proportional to the time,
Q∝t
And heat flow is inversly proportional to the length of the rod,
Q∝1L
Jab inn sabo combine krenge toh banega,
Q∝A(T1−T2)tL
Therefore,
Heat flow, Q=KA(T1−T2)tL
Yaha prr k proportionality constant hai jisko hum thermal conductivity of the material bolte hai,
Jitni jyada Kki vale hogi ,utni jyada heat conduct hogi.SI unit of K is Js–1m–1K–1 or Wm–1K–1.
K ki ek common unit bhi hoti hai voh hai calcm−(1)s−1∘C−1.
HEAT CURRENT
Isko hum define krenge “Rate of flow of heat is called heat current”,mtlb heat ek given time me kitna flow kr rhi hai,usko hum bolte hai heat current.
Isko hum ‘H’se denote krte hai.
H=Qt or H=KAT1−T2L
CONVECTION
Convection kevl fluids me possible hota hai,mtlb ki jo deform hone ki ability rakhta hai usme.In convection, “heat is transferred from one place to the other by the actual motion of heated material”, iska mtlb hai baccho ki koi material hai jo ki already heated hai,uss heat ka ek jagah se dusri jagah transfer hona kevl material ke actual motion ki wajah se,use hum kehte hai convention.
Jese ki aapne dekh rakha hoga ki hot air blower hota hai,toh air ko hum heat krte hai air blower ke heating element se or uss heated air ko hum fan se bahar nikalte hai,phir uss hot air se hum dusri cheezo ko heat transfer krte hai, toh iss heat transfer ko humne forcely kiya with the help of heating device, toh ese heat ke transfer ko hum forced convection bolte hai. Or jo jaha hume kisi force ka use nhi krna hota hai ya convection naturally density ke difference ki wajah se hota hai ,use hum natural convection or free convection bote hai.
Natural convection ko hum example se samjhenge, toh gravity important role play krti hai,voh kese,
Jab kisi fluid ko neeche se heat kiya jata hai,toh bottom layer ka temperature increase hoga and voh expand kregi,expand krne se volume increase hoga bottom layer ka and density decrease ho jaegi,aur phir ye bottom layer uss fluid ki topmost layer ko replace krdegi,and ye process chti rahegi,ise hum natural convection bolte hai.
OMR (One Minute Revision)
- * The specific heat capacity of a substance is defined by
s=ΔQmΔT
* Cp = molar specific heat capacity at constant pressure. * Cv = molar specific heat capacity at constant volume. * The SI unit of K (thermal conductivity) is Js–1m–1K–1 or Wm–1K–1.
RADIATION
Radiation bhi ek tareeka hai heat transfer ka,lekin isme hume kisi medium ki jrurat nhi hoti hai jese ki convection and conduction me rehti thi, toh ise hum define kr sakte hai “Heat transfer occurs without any medium or no medium is required to transfer the heat”, mtlb bina medium ka use kiye hum heat ko transfer krte hai use hum radiation kehte hai.Iska simple sa example lete hai hum,jese ki earth and sun ke beech me bhut distance hai,phir bhi sun se heat earth tk aajati hai,sun se jo heat earth tk aati hai voh bina kisi medium ki help se aati hai,iska mtlb hua ki earth prr heat radiation ki wajah se aati hai aur voh electro magnetic wave ke form me aati hai.
Ab radiation kese hoga isme kya hoga,ye sab hum pta krenge,toh baccho iski ek theory di gyi,
PREVOST THEORY OF EXCHANGE
Prevost ne kaha ki “ all bodies emits thermal radiation at all temperature” and “all bodies absorbs thermal/heat radiations falling on it at all temperature”,mtlb hai baccho ki prevost ne kaha ki duniya ki saari bodies jese pen,paper,human body vagerah vagerah ,ye sab heat radiate bhi krti hai and absorb bhi krti hai har temperature prr.Ab konsi boy kitni heat radiate krti hai ya absorb krti hai ye uss body ke material and temperature prr depend krega,that is “ amount of heat emitted/absorbed is depend upon temperature and material of the body”.
Maan lijiye ki surrounding ka temperature body ke temperature se jyada hai, iska mtlb body heat absorb jyada kregi as compare to emission and agr surrounding ka temperature body ke temperature se kam hai,toh iska mtlb body heat emit jyada kregi as compare ki absorbtion. Ab inn dono condition me ek time esa aaega ki dono surrounding and body thermal equilibrium me aajaenge (dono ka temperature same ho jaega),uss time voh body jitna heat absorb kregi utni hi heat emit bhi kregi, “amount of heat absorbed = amount of heat emitted”.
BLACK BODY RADIATION
Agr definition ki baat krein toh bolenge “ Body which absorb all radiations falling on it at any temperature at any incident angle” mtlb hai ki esi body jo saare radiation ko absorb krle jo bhi uske upar aa rhe hai ,kisi bhi temperature prr and kisi bhi angle se. Black body zero reflection deti hai,mtlb ki jitni radiation uske upar aaegi voh poori ki poori absorb krlegi and kuch bhi radiation ko vaps reflect nhi kregi and black body zero transmittence bhi show krta hai ,mtlb ki uss body se koi bhi radiation bahar nhi jaati hai,sab ki sab absorb ho jaati hai.Baccho iska naam black body isliye rakha gya kyunki hum sabko pta hai ki black colour bhut accha absorber hota hai (black colour is a good absorber),yhi dekhte hue iska naam blac body radiation rakha gya,mtlb hai ki jo body bhut acchi absorber hoti hai or poori ki poori radiation ko absorb krleta hai.Ab iska mtlb ye nhi hai ki body black colou ki hi hogi,voh kisi bhi colour ki ho sakti hai jese red,blue,green,orange anything.
WIENS DISPLACEMENT LAW

Baccho jesa ki aap upar dekh rhe honge ki intensity vs wavelength ka graph diya hua hai,toh phle hum isko samjhenge ki ye hai kya,
Jesa ki aap sabhi jaante hai ki kisi bhi body ko hum heat krte hai toh different different wavelengths waali intensity nikalti hai (radiation ka mtlb hi hota hai ki electromagnetic wave ki through heat transfer hona and waves ki wavelengths toh hoti hi hai).
Toh humne ek experiment kiya or kisi ek body ko kisi temerature prr heat kiya( maan lijiye voh temperature hai T1) , toh dekha gya ki multiple wavelength ki radiations nikli,or usme se sabse jyada radiation jis wavelength ki nikli use humne λmax1 se denote kiya,or ye same process humne different different temperatures prr perfore kari toh dekha ki T2 prr wavelength λmax2 hai and T3 prr wavelength λmax3 hai.
Hum temperature ko iss form me rakha , T3>T2>T1 toh hume ta chla ki wavelength λmax1>λmax2>λmax3 aai.
Mtlb jese jese temperature increase krte jaenge vese vese sabse jyada radiation emit krne waali wavelength decrease hoti jaegi,
Ab wiens ne kya dekha ki jab λmax and T ka hum product krte hai for any value of temperature, voh humesha constant aai
. That means ,
λmaxT = constant
Ye relation wiens ne dekha tha isliye ise wiens displacement law bolte hai.
The value of the constant (Wien’s constant) is 2.9×10–3mK .
STEFAN-BOLTZMANN LAW
Ye law hume btata hai ki for a perfectly black body,
Intensity of radiation is directiy proportional to the fourth power of temperature,
QAt∝T4
QAt=σ(T4)
Now, Q/t = sigmaA(T^4)<b>,<br>Andthiswecansay,thee≠rgyemiedperunittimeis≺br><b>H = sigmaA(T^4)<b>,thisisstefans−bo<zma∩lawforperfectlyblackbodyandtheconstantsigmaiscal≤dStefan−Bo<zma∩constant.Itsvalue∈SIunitsis<b>5.67 × 10–8 W m^(–2) K^(–4) <b><br>AndagrkoibodykatemperatureThaiorsurround∈gskatemperatureTshai,→hjoe≠rgyperunittimeradiatehogiusehumlikhen≥,<b>H = sigmaA(T^4-T^s)<b>,<br>Agrkisibodykiemissivity<b>e<b>hai→hmodifiykrkehumlikhen≥,<br><b>H = sigmaeA(T^4-T^s)<b><br>Where<b>0<=e<=1
POINT 1
Conduction:Conduction is the mechanism of transfer of heat between two adjacent parts of a body because
of their temperature difference.
Heat current:Rate of flow of heat is called heat current.
Convection:Heat is transferred from one place to the other by the actual motion of heated material.
Forced convection: If
the heated material is forced to move, say by a blower
or a pump, the process of heat transfer is called forced
convection.
Radiation:Heat transfer occurs without any medium or no medium is required to transfer the heat.
Black body:Body which absorb all radiations falling on it at any temperature at any incident angle.
POINT 1
Conduction:Conduction is the mechanism of transfer of heat between two adjacent parts of a body because
of their temperature difference.
Heat current:Rate of flow of heat is called heat current.
Convection:Heat is transferred from one place to the other by the actual motion of heated material.
Forced convection: If
the heated material is forced to move, say by a blower
or a pump, the process of heat transfer is called forced
convection.
Radiation:Heat transfer occurs without any medium or no medium is required to transfer the heat.
Black body:Body which absorb all radiations falling on it at any temperature at any incident angle.
POINT 1
Conduction:Conduction is the mechanism of transfer of heat between two adjacent parts of a body because
of their temperature difference.
Heat current:Rate of flow of heat is called heat current.
Convection:Heat is transferred from one place to the other by the actual motion of heated material.
Forced convection: If
the heated material is forced to move, say by a blower
or a pump, the process of heat transfer is called forced
convection.
Radiation:Heat transfer occurs without any medium or no medium is required to transfer the heat.
Black body:Body which absorb all radiations falling on it at any temperature at any incident angle.
EXAMPLE 1
What is the temperature of the steel-copper junction in the steady state of the system shown in Fig. 11.15. Length of the steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =300∘C, temperature of the other end = 0∘C. The area of cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2Js–1m–1K–1, and of copper =385Js–1m–1K–1).
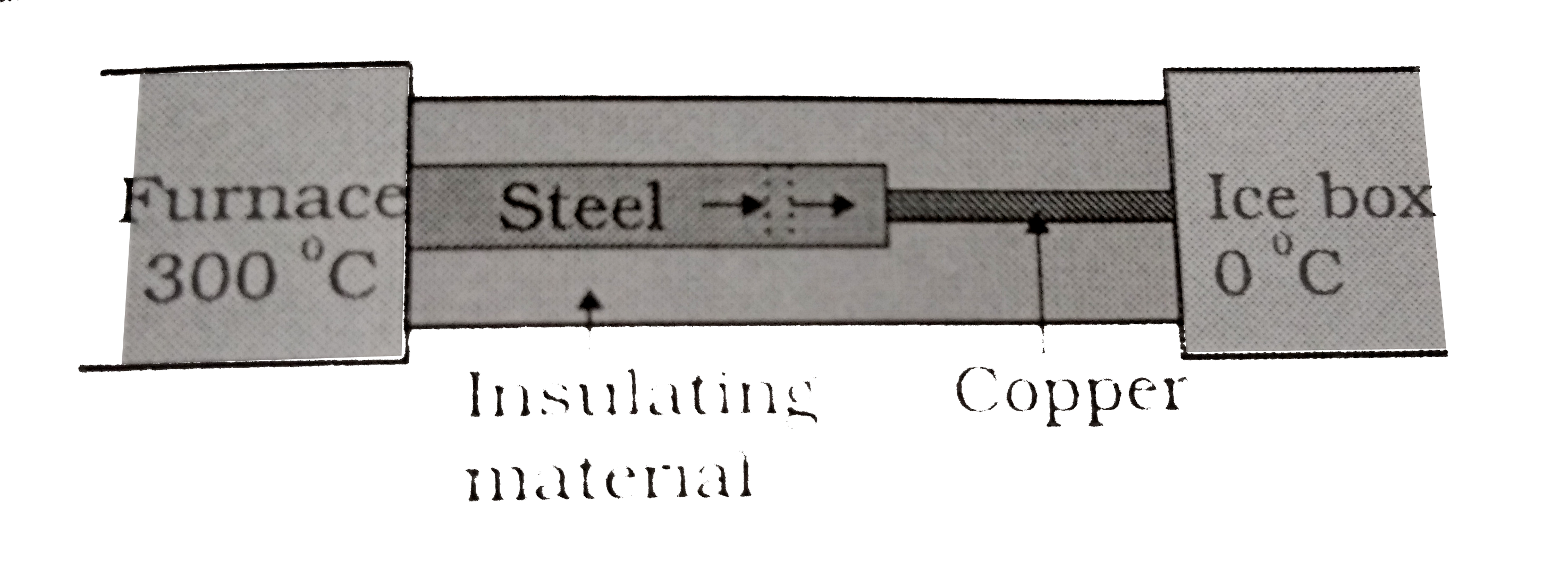
The insulating material around the rods reduces heat loss from the sides of the rods. Therefore, heat flows only along the length of the rods. Consider any cross section of the rod. In the steady state, heat flowing into the element must equal the heat flowing out of it, otherwise there would be a net gain or loss of heat by the element and its temperature would not be steady. Thus in the steady state, rate of heat flowing across a cross section of the rod is the same at every point along the length of the combined steel-copper rod. Let T be the temperature of the steel-copper junction in the steady state. Then,
K1A1(300−T)L1=K2A2(T−O)L2
where 1 and 2 refer to the steel and copper rod respectively. For A1=2A2,L1=15.0cm,L2=10.0cm,K1=50.2Js–1m–1K–1,K2=385Js–1m–1K–1, we have
50.2×2(300−T)15=385T10
which gives T=44.4∘C
EXAMPLE 1
What is the temperature of the steel-copper junction in the steady state of the system shown in Fig. 11.15. Length of the steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =300∘C, temperature of the other end = 0∘C. The area of cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2Js–1m–1K–1, and of copper =385Js–1m–1K–1).

The insulating material around the rods reduces heat loss from the sides of the rods. Therefore, heat flows only along the length of the rods. Consider any cross section of the rod. In the steady state, heat flowing into the element must equal the heat flowing out of it, otherwise there would be a net gain or loss of heat by the element and its temperature would not be steady. Thus in the steady state, rate of heat flowing across a cross section of the rod is the same at every point along the length of the combined steel-copper rod. Let T be the temperature of the steel-copper junction in the steady state. Then,
K1A1(300−T)L1=K2A2(T−O)L2
where 1 and 2 refer to the steel and copper rod respectively. For A1=2A2,L1=15.0cm,L2=10.0cm,K1=50.2Js–1m–1K–1,K2=385Js–1m–1K–1, we have
50.2×2(300−T)15=385T10
which gives T=44.4∘C
EXAMPLE 1
What is the temperature of the steel-copper junction in the steady state of the system shown in Fig. 11.15. Length of the steel rod = 15.0 cm, length of the copper rod = 10.0 cm, temperature of the furnace =300∘C, temperature of the other end = 0∘C. The area of cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel =50.2Js–1m–1K–1, and of copper =385Js–1m–1K–1).

The insulating material around the rods reduces heat loss from the sides of the rods. Therefore, heat flows only along the length of the rods. Consider any cross section of the rod. In the steady state, heat flowing into the element must equal the heat flowing out of it, otherwise there would be a net gain or loss of heat by the element and its temperature would not be steady. Thus in the steady state, rate of heat flowing across a cross section of the rod is the same at every point along the length of the combined steel-copper rod. Let T be the temperature of the steel-copper junction in the steady state. Then,
K1A1(300−T)L1=K2A2(T−O)L2
where 1 and 2 refer to the steel and copper rod respectively. For A1=2A2,L1=15.0cm,L2=10.0cm,K1=50.2Js–1m–1K–1,K2=385Js–1m–1K–1, we have
50.2×2(300−T)15=385T10
which gives T=44.4∘C
EXAMPLE 2
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm–1K–1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm–1K–1) are soldered end to end as shown in Fig. 11.16. The free ends of the iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar, and (iii) the heat current through the compound bar.
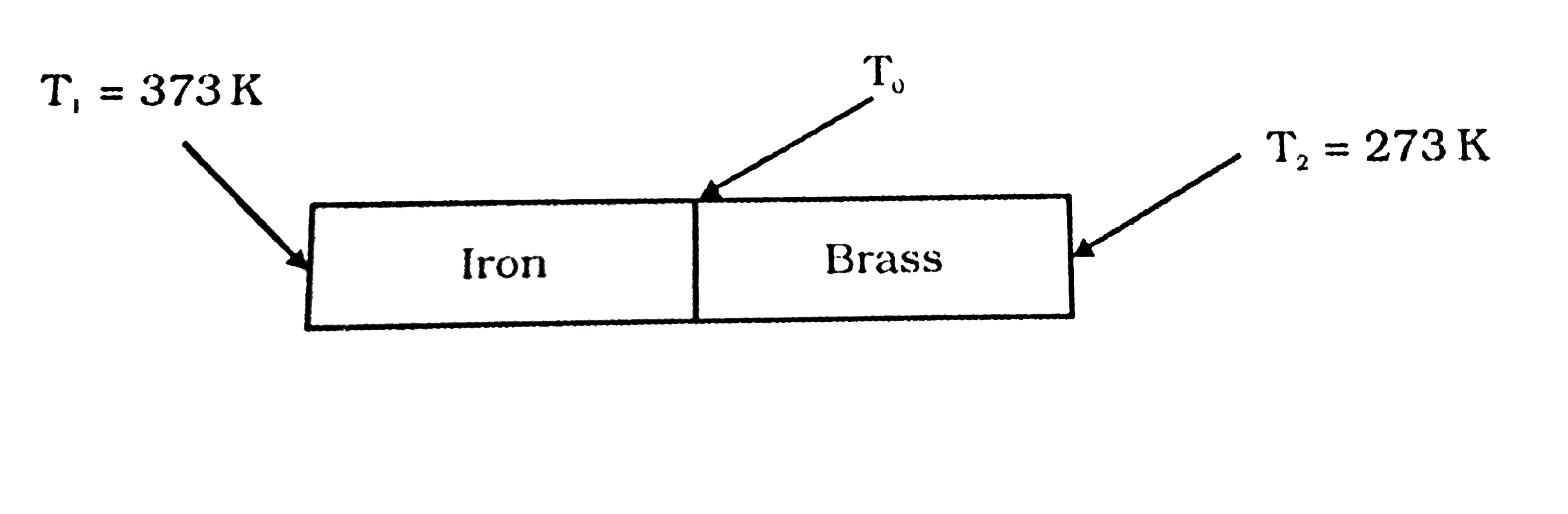
Given, L1=L2=L=0.1m,A1=A2=A=0.02m2K1=79Wm–1K–1,K2=109Wm–1K–1,T1=373K,andT2=273K.
Under steady state condition, the heat current (H1) through iron bar is equal to the heat current (H2) through brass bar.
So, H=H1=H2
K1A1T1−T0L1=K2A2T0−T2L2
For A1=A2=A and L1=L2=L, this equation leads to K1(T1−T0)=K2(T0−T2)
Thus the junction temperature T0 of the two bars is
T0=(K1T1+K2T2(K1+K2))
Using this equation, the heat current H through either bar is
H=K1A(T1−T0)L=K2A(T0−T2)L
(K1K2K1+K2)A(T1T2)L=A(T1−T2)L(1K1+1K2)
Using these equations, the heat current H′ through the compound bar of length L1+L2=2L and the equivalent thermal conductivity K′, of the compound bar are given by
H'=K'A(T1−T2)2L=H
K'=2K1K2K1+K2
(i) T0=(K1T1+K2T2)(K1+K2)
(79Wm−1K−1)(373K)+(109Wm−1K−1)(273K)79Wm−1K−1+109Wm−1K−1
=315 K
(ii) K'=2K1K2K1+K2
=2×(79WM−1K−1)×(109Wm−1K−1)79Wm−1K−1+109Wm−1K−1
=91.6Wm−1K−1
(iii) H'=H=K'A(T1−T2)2L
=(91.6Wm−1K−1)×(0.02m2)×(373K−273K)2×(0.1m)
916.1 W
EXAMPLE 2
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm–1K–1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm–1K–1) are soldered end to end as shown in Fig. 11.16. The free ends of the iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar, and (iii) the heat current through the compound bar.

Given, L1=L2=L=0.1m,A1=A2=A=0.02m2K1=79Wm–1K–1,K2=109Wm–1K–1,T1=373K,andT2=273K.
Under steady state condition, the heat current (H1) through iron bar is equal to the heat current (H2) through brass bar.
So, H=H1=H2
K1A1T1−T0L1=K2A2T0−T2L2
For A1=A2=A and L1=L2=L, this equation leads to K1(T1−T0)=K2(T0−T2)
Thus the junction temperature T0 of the two bars is
T0=(K1T1+K2T2(K1+K2))
Using this equation, the heat current H through either bar is
H=K1A(T1−T0)L=K2A(T0−T2)L
(K1K2K1+K2)A(T1T2)L=A(T1−T2)L(1K1+1K2)
Using these equations, the heat current H′ through the compound bar of length L1+L2=2L and the equivalent thermal conductivity K′, of the compound bar are given by
H'=K'A(T1−T2)2L=H
K'=2K1K2K1+K2
(i) T0=(K1T1+K2T2)(K1+K2)
(79Wm−1K−1)(373K)+(109Wm−1K−1)(273K)79Wm−1K−1+109Wm−1K−1
=315 K
(ii) K'=2K1K2K1+K2
=2×(79WM−1K−1)×(109Wm−1K−1)79Wm−1K−1+109Wm−1K−1
=91.6Wm−1K−1
(iii) H'=H=K'A(T1−T2)2L
=(91.6Wm−1K−1)×(0.02m2)×(373K−273K)2×(0.1m)
916.1 W
EXAMPLE 2
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm–1K–1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm–1K–1) are soldered end to end as shown in Fig. 11.16. The free ends of the iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar, and (iii) the heat current through the compound bar.

Given, L1=L2=L=0.1m,A1=A2=A=0.02m2K1=79Wm–1K–1,K2=109Wm–1K–1,T1=373K,andT2=273K.
Under steady state condition, the heat current (H1) through iron bar is equal to the heat current (H2) through brass bar.
So, H=H1=H2
K1A1T1−T0L1=K2A2T0−T2L2
For A1=A2=A and L1=L2=L, this equation leads to K1(T1−T0)=K2(T0−T2)
Thus the junction temperature T0 of the two bars is
T0=(K1T1+K2T2(K1+K2))
Using this equation, the heat current H through either bar is
H=K1A(T1−T0)L=K2A(T0−T2)L
(K1K2K1+K2)A(T1T2)L=A(T1−T2)L(1K1+1K2)
Using these equations, the heat current H′ through the compound bar of length L1+L2=2L and the equivalent thermal conductivity K′, of the compound bar are given by
H'=K'A(T1−T2)2L=H
K'=2K1K2K1+K2
(i) T0=(K1T1+K2T2)(K1+K2)
(79Wm−1K−1)(373K)+(109Wm−1K−1)(273K)79Wm−1K−1+109Wm−1K−1
=315 K
(ii) K'=2K1K2K1+K2
=2×(79WM−1K−1)×(109Wm−1K−1)79Wm−1K−1+109Wm−1K−1
=91.6Wm−1K−1
(iii) H'=H=K'A(T1−T2)2L
=(91.6Wm−1K−1)×(0.02m2)×(373K−273K)2×(0.1m)
916.1 W
EXAMPLE 3
One face of a copper cube of edge 10 cm is maintained at 100∘C and the opposite face is maintained at 0∘C. All other surfaces are covered with an insulating material. Find the amount of heat flowing per second through the cube. Thermal conductivity of copper is 385Wm−1C−1.
The heat flows from the hotter face towards the collder face. The area of cross section perpendicular to the heat flow is A=(10cm)2. The amount of heat flowing per second is ΔQΔt=KAT1−T2x . =(385Wm−1^(@)C^(-1))xx(0.1m)^(2)xx((100^(@)C-0^(@)C))/(0.1m).=3850W .
EXAMPLE 3
One face of a copper cube of edge 10 cm is maintained at 100∘C and the opposite face is maintained at 0∘C. All other surfaces are covered with an insulating material. Find the amount of heat flowing per second through the cube. Thermal conductivity of copper is 385Wm−1C−1.
The heat flows from the hotter face towards the collder face. The area of cross section perpendicular to the heat flow is A=(10cm)2. The amount of heat flowing per second is ΔQΔt=KAT1−T2x . =(385Wm−1^(@)C^(-1))xx(0.1m)^(2)xx((100^(@)C-0^(@)C))/(0.1m).=3850W .
EXAMPLE 3
One face of a copper cube of edge 10 cm is maintained at 100∘C and the opposite face is maintained at 0∘C. All other surfaces are covered with an insulating material. Find the amount of heat flowing per second through the cube. Thermal conductivity of copper is 385Wm−1C−1.
The heat flows from the hotter face towards the collder face. The area of cross section perpendicular to the heat flow is A=(10cm)2. The amount of heat flowing per second is ΔQΔt=KAT1−T2x . =(385Wm−1^(@)C^(-1))xx(0.1m)^(2)xx((100^(@)C-0^(@)C))/(0.1m).=3850W .
EXAMPLE 4
The light from the sun is found to have a maximum intensity near the wavelength of 470nm. Assuming that the surface o f the sun emits as a blackbody, calculate the temperature of the surface of the sun.
For a blackbody, λmT=0.288cmK .thus, T=0.288cmK470nm=6130K.
EXAMPLE 4
The light from the sun is found to have a maximum intensity near the wavelength of 470nm. Assuming that the surface o f the sun emits as a blackbody, calculate the temperature of the surface of the sun.
For a blackbody, λmT=0.288cmK .thus, T=0.288cmK470nm=6130K.
EXAMPLE 4
The light from the sun is found to have a maximum intensity near the wavelength of 470nm. Assuming that the surface o f the sun emits as a blackbody, calculate the temperature of the surface of the sun.
For a blackbody, λmT=0.288cmK .thus, T=0.288cmK470nm=6130K.
EXAMPLE 5
A blackbody of surface area 10cm2 is heated to 127∘C and is suspended in a room at temperature 27∘C calculate the initial rate of loss of heat from the body to the room.
For a blackbody at temperature T, the rate of emission is u=σAT4 . When it is kept in a room at temperature T0, the rate of absorption is u0=σA(T4−(t40) .Here A=10×104m2 , T=400K and T0=300K . Thus, u−u0
=(5.67×10−8Wm−2K−4(10×10−4m2)(4004−(3004)K4
=0.99W.
EXAMPLE 5
A blackbody of surface area 10cm2 is heated to 127∘C and is suspended in a room at temperature 27∘C calculate the initial rate of loss of heat from the body to the room.
For a blackbody at temperature T, the rate of emission is u=σAT4 . When it is kept in a room at temperature T0, the rate of absorption is u0=σA(T4−(t40) .Here A=10×104m2 , T=400K and T0=300K . Thus, u−u0
=(5.67×10−8Wm−2K−4(10×10−4m2)(4004−(3004)K4
=0.99W.
EXAMPLE 5
A blackbody of surface area 10cm2 is heated to 127∘C and is suspended in a room at temperature 27∘C calculate the initial rate of loss of heat from the body to the room.
For a blackbody at temperature T, the rate of emission is u=σAT4 . When it is kept in a room at temperature T0, the rate of absorption is u0=σA(T4−(t40) .Here A=10×104m2 , T=400K and T0=300K . Thus, u−u0
=(5.67×10−8Wm−2K−4(10×10−4m2)(4004−(3004)K4
=0.99W.
NEWTON’S LAW OF COOLING
Isko samjhne ke liye hum maan lete hai ki ek body hai jiska temperature surrounding ke temperature se jyada hai,toh hoga ye ki body se heat tansfer hoke surrounding me jaegi or body surrounding ke temperature ka hona chahegi.
Toh iss jis rate se body cool ho rhi hai or the rate of loss of heat is directly proportional hoga temperature difference between body and surrounding,
Means −dTdt∝Tb−Ts , this is newtons law of cooling.
Therefore , −dTdt=K(Tb−Ts)............................................eq1
Yaha prr K ek constant hai jiski value depend kregi area and nature of the surface of the body.
Maan lete hai ki ek body hai jiska mass m hai and specific heat capacity s or ye body temperature T2 prr hai. Aur hum maan lete hai ki surrounding ka temperature T1 hai,
Agr small temperature dT2 fall hota hai in time dt, toh jo heat ka amount loss hoga voh hoga,
dQ=msdT…………………………………………eq2<b><br><br>Jabeq^1andeq^2kocomparekren≥→hba¬a,<br><b>log_e (T_2 – T_1 ) = – K t + c<b><br>orT_2 = T_1 + (C^′)(e –Kt)<br>where<b>C^′ = e c
Is se hum body ka cooling ka time nikaal sakte hai for a particular range of temperature.
NEWTON’S LAW OF COOLING
Isko samjhne ke liye hum maan lete hai ki ek body hai jiska temperature surrounding ke temperature se jyada hai,toh hoga ye ki body se heat tansfer hoke surrounding me jaegi or body surrounding ke temperature ka hona chahegi.
Toh iss jis rate se body cool ho rhi hai or the rate of loss of heat is directly proportional hoga temperature difference between body and surrounding,
Means −dTdt∝Tb−Ts , this is newtons law of cooling.
Therefore , −dTdt=K(Tb−Ts)............................................eq1
Yaha prr K ek constant hai jiski value depend kregi area and nature of the surface of the body.
Maan lete hai ki ek body hai jiska mass m hai and specific heat capacity s or ye body temperature T2 prr hai. Aur hum maan lete hai ki surrounding ka temperature T1 hai,
Agr small temperature dT2 fall hota hai in time dt, toh jo heat ka amount loss hoga voh hoga,
dQ=msdT…………………………………………eq2<b><br><br>Jabeq^1andeq^2kocomparekren≥→hba¬a,<br><b>log_e (T_2 – T_1 ) = – K t + c<b><br>orT_2 = T_1 + (C^′)(e –Kt)<br>where<b>C^′ = e c
Is se hum body ka cooling ka time nikaal sakte hai for a particular range of temperature.
NEWTON’S LAW OF COOLING
Isko samjhne ke liye hum maan lete hai ki ek body hai jiska temperature surrounding ke temperature se jyada hai,toh hoga ye ki body se heat tansfer hoke surrounding me jaegi or body surrounding ke temperature ka hona chahegi.
Toh iss jis rate se body cool ho rhi hai or the rate of loss of heat is directly proportional hoga temperature difference between body and surrounding,
Means −dTdt∝Tb−Ts , this is newtons law of cooling.
Therefore , −dTdt=K(Tb−Ts)............................................eq1
Yaha prr K ek constant hai jiski value depend kregi area and nature of the surface of the body.
Maan lete hai ki ek body hai jiska mass m hai and specific heat capacity s or ye body temperature T2 prr hai. Aur hum maan lete hai ki surrounding ka temperature T1 hai,
Agr small temperature dT2 fall hota hai in time dt, toh jo heat ka amount loss hoga voh hoga,
dQ=msdT…………………………………………eq2<b><br><br>Jabeq^1andeq^2kocomparekren≥→hba¬a,<br><b>log_e (T_2 – T_1 ) = – K t + c<b><br>orT_2 = T_1 + (C^′)(e –Kt)<br>where<b>C^′ = e c
Is se hum body ka cooling ka time nikaal sakte hai for a particular range of temperature.
EXAMPLE 6
A pan filled with hot food cools from 94∘C to 86∘C in 2 minutes when the room temperature is at 20∘C. How long will it take to cool from 71∘C to 69∘C?
The average temperature of 9∘C and 86∘Cis90∘C, which is 70∘C above the room temperature. Under these conditions the pan cools 8∘C in 2 minutes
Using Eq. (11.17), we have
Change in temperatureTimeKΔT
8∘C2 min=K(70∘C)
The average of 69∘C and 71∘C is 70∘C, which is 50∘C above room temperature. K is the same for this situation as for the original
2∘CTime=K(50∘C)
When we divide above two equations, we have
8∘C/2min2∘C/time=K(70∘C)K(70∘C)
Time = 0.7 min
42s
EXAMPLE 6
A pan filled with hot food cools from 94∘C to 86∘C in 2 minutes when the room temperature is at 20∘C. How long will it take to cool from 71∘C to 69∘C?
The average temperature of 9∘C and 86∘Cis90∘C, which is 70∘C above the room temperature. Under these conditions the pan cools 8∘C in 2 minutes
Using Eq. (11.17), we have
Change in temperatureTimeKΔT
8∘C2 min=K(70∘C)
The average of 69∘C and 71∘C is 70∘C, which is 50∘C above room temperature. K is the same for this situation as for the original
2∘CTime=K(50∘C)
When we divide above two equations, we have
8∘C/2min2∘C/time=K(70∘C)K(70∘C)
Time = 0.7 min
42s
EXAMPLE 6
A pan filled with hot food cools from 94∘C to 86∘C in 2 minutes when the room temperature is at 20∘C. How long will it take to cool from 71∘C to 69∘C?
The average temperature of 9∘C and 86∘Cis90∘C, which is 70∘C above the room temperature. Under these conditions the pan cools 8∘C in 2 minutes
Using Eq. (11.17), we have
Change in temperatureTimeKΔT
8∘C2 min=K(70∘C)
The average of 69∘C and 71∘C is 70∘C, which is 50∘C above room temperature. K is the same for this situation as for the original
2∘CTime=K(50∘C)
When we divide above two equations, we have
8∘C/2min2∘C/time=K(70∘C)K(70∘C)
Time = 0.7 min
42s
EXAMPLE 7
A bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
The situation is shown in figure. Let the temperature at the junction be (theta) (on celsius scale). The same heat current passes through the copper and the steel rods. Thus,
ΔQΔt=KcuA(100∘C−θ)75cm=KsteelAθ125cm . or, Kcu(100∘C−θ)75=Ksteelθ125. or, 100∘C−θθ=75Ksteel125Kcu=35×46386 . or, θ=93∘C . The rate of heat flow is
ΔQΔt=KsteelAθ125cm . =((46Js−1m−1^(@)C^(-1))(pixx1cm^(2))xx93^(@)C)/(125cm).=1.07Js^(-1) .

EXAMPLE 7
A bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
The situation is shown in figure. Let the temperature at the junction be (theta) (on celsius scale). The same heat current passes through the copper and the steel rods. Thus,
ΔQΔt=KcuA(100∘C−θ)75cm=KsteelAθ125cm . or, Kcu(100∘C−θ)75=Ksteelθ125. or, 100∘C−θθ=75Ksteel125Kcu=35×46386 . or, θ=93∘C . The rate of heat flow is
ΔQΔt=KsteelAθ125cm . =((46Js−1m−1^(@)C^(-1))(pixx1cm^(2))xx93^(@)C)/(125cm).=1.07Js^(-1) .

EXAMPLE 7
A bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
The situation is shown in figure. Let the temperature at the junction be (theta) (on celsius scale). The same heat current passes through the copper and the steel rods. Thus,
ΔQΔt=KcuA(100∘C−θ)75cm=KsteelAθ125cm . or, Kcu(100∘C−θ)75=Ksteelθ125. or, 100∘C−θθ=75Ksteel125Kcu=35×46386 . or, θ=93∘C . The rate of heat flow is
ΔQΔt=KsteelAθ125cm . =((46Js−1m−1^(@)C^(-1))(pixx1cm^(2))xx93^(@)C)/(125cm).=1.07Js^(-1) .

SUMMARY
* The three modes of heat transfer are conduction, convection and radiation.
* Newton’s Law of Cooling says that the rate of cooling of a body is proportional to the excess temperature of the body over the surroundings :
dQdt=−K(T1−T2)
Where T1 is the temperature of the surrounding medium and T2 is the temperature of the body.
SUMMARY
* The three modes of heat transfer are conduction, convection and radiation.
* Newton’s Law of Cooling says that the rate of cooling of a body is proportional to the excess temperature of the body over the surroundings :
dQdt=−K(T1−T2)
Where T1 is the temperature of the surrounding medium and T2 is the temperature of the body.
SUMMARY
* The three modes of heat transfer are conduction, convection and radiation.
* Newton’s Law of Cooling says that the rate of cooling of a body is proportional to the excess temperature of the body over the surroundings :
dQdt=−K(T1−T2)
Where T1 is the temperature of the surrounding medium and T2 is the temperature of the body.
