Gravitation Potential, Energy and Escape Velocity from UNIVERSAL BOOK DEPOT 1960 PHYSICS (HINGLISH) GRAVITATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| UNIVERSAL BOOK DEPOT 1960 PHYSICS (HINGLISH) | Gravitation Potential, Energy and Escape Velocity |
| Medium | English |
| Academic Year | 2023-2024 |
Question 41
The value of ‘ g ’ at a particular point is 9.8m/s2 . Suppose the earth suddenly shrinks uniformly to half its present size without losing any mass. The value of ‘ g ’ at the same point (assuming that the distance of the point from the centre of earth does not shrink) will now beView SolutionQuestion 80
Assume that the acceleration due to gravity on the surface of the moon is 0.2 times the acceleration due to gravity on the surface of the earth. If Re is the maximum range of a projectile on the earth's surface, what is the maximum range on the surface of the moon for the same velocity of projectionView SolutionQuestion 215
In the following four periods
(i) Time of revolution of a satellite just above the earth's surface (Tst)
(ii) Period of oscillation of mass inside the tunnel bored along the diameter of the earth (Tma)
(iii) Period of simple pendulam having a length equal to the earth's raduis in a unifrom field of 9.8N/kg(Tsp)
(iv) Period of an infinite length simple pendulam in the earth's real gravitational field (Tis)View SolutionQuestion 250
Figure shows the motion of a planet around the Sun S in an elliptical orbit with the Sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If t1 and t2 represent the time taken for the planet to move from a to b and c to d, respectively then
 View Solution
View SolutionQuestion 300
Imagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to R−5/2, then
(a) T2 is proportional to R2
(b) T2 is proportional to R7/2
(c) T2 is proportional to R3/3
(d) T2 is proportional to R3.75.View SolutionQuestion 312
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
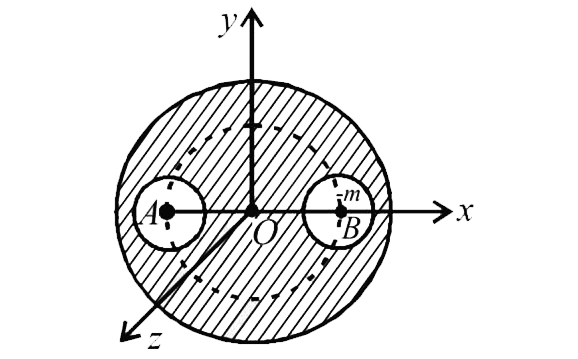 View Solution
View SolutionQuestion 314
A projectile is projectile with velocity kve in vertically upward direction from the ground into the space (ve is escape velocity and k<1). If air resistance is considered to be negligible then the maximum height from the centre of earth to which it can go, will be : (R=raduis of earth) View SolutionQuestion 321
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]View SolutionQuestion 323
Suppose the acceleration due to gravity at earth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?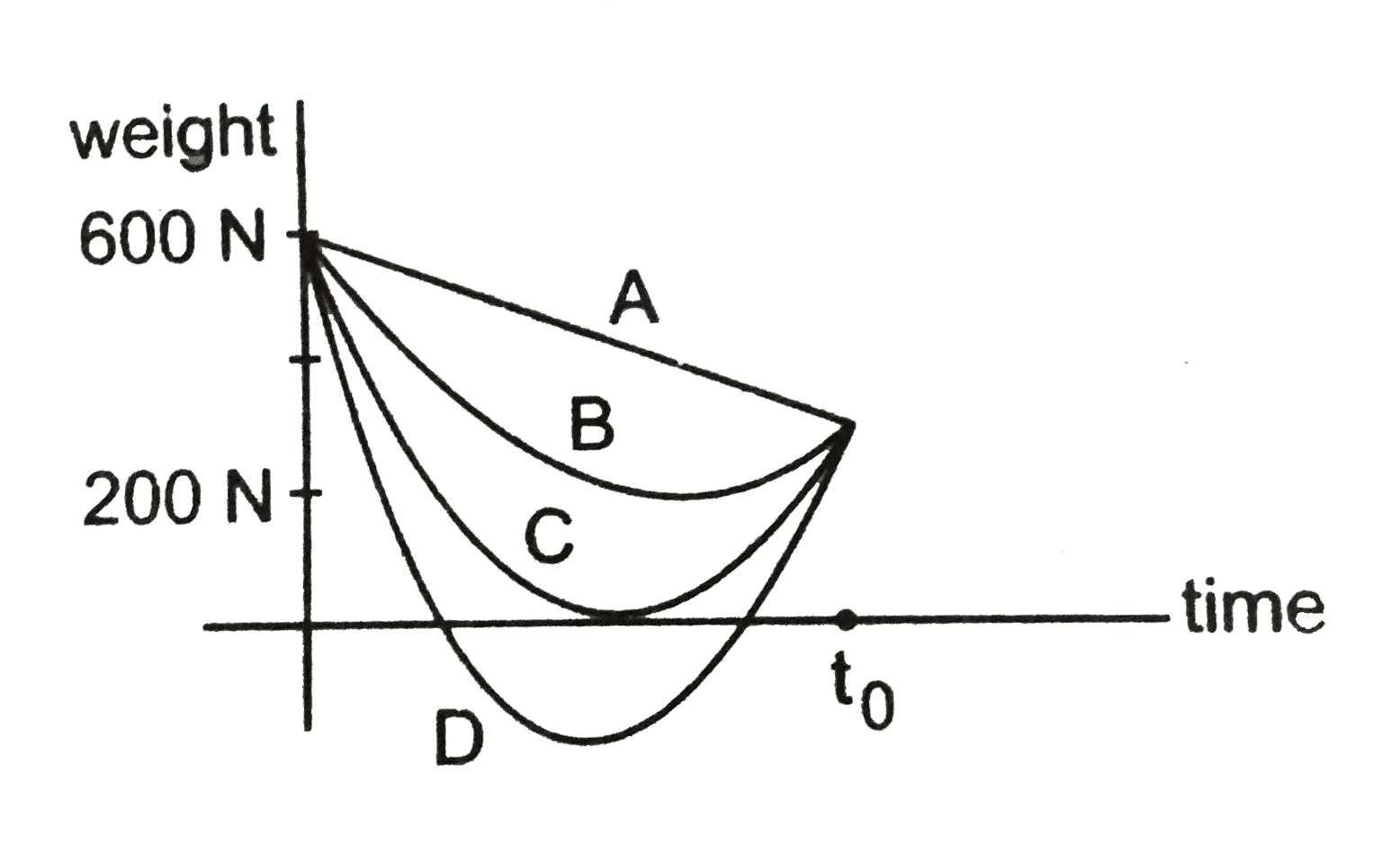 View Solution
View SolutionQuestion 348
Assertion: When distance between bodies is doubled and also mass of each body is also doubled, gravitational force between them remains the same.
Reason: According to Neweton's law gravitational, force is directely proportional to mass of bodies and inversely proportional to square of distance between them.View Solution
_S01_003_Q01.png)