रैखिक प्रोग्रामन कक्षा 12 गणित
भूमिका
बच्चों! पिछली कक्षाओं में हमनें रैखिक असमिकाओं के बारे में पढ़ा हैं, एक असमिका, दो वास्तविक संख्याओं या दो बीजीय व्यंजकों में <, ≤, > या ≥ के चिह्न के प्रयोग से बनती हैं साथ ही पिछली कक्षाओं में हमनें दो चरों वाले रैखिक असमिकाओं व उनके निकायों के आलेखीय निरूपण से हल ज्ञात करना सीखा था। इस अध्याय में हम रैखिक समीकरणों व असमिकाओं का प्रयोग कर दैनिक जीवन में आने वाले उत्पादन, आहार, परिवहन आदि प्रकार के समस्या के (लाभ) अधिकतम अथवा (लागत) न्यूनतम मान ज्ञात करने का प्रयास करेंगे। इष्टतमकारी समस्याओ में लाभ का अधिकतम मान, न्यूनतम लागत, न्यूनतम हानि आदि ज्ञात किया जाता है। साथ ही कुछ इस प्रकार की समस्या देखेंगे, जिनमें असमिकाये तथा प्रतिबंध ज्ञात हो, उनके लिए भी न्यूनतमीकरण अथवा अधिकतमीकरण कर मान ज्ञात करना सीखेंगे।।
आइए बच्चों रैखिक प्रोग्रामन को समझते हैं और करीब से...
बच्चों, रैखिक प्रोग्रामिंग में हम रैखिक प्रोग्रामिंग समस्या को हल करने के बारे में देखेंगे।
रैखिक प्रोग्रामिंग समस्या वह समस्या हैं जिसमें हमें कई चर के रैखिक फलनों का इष्टतम मान (अधिकतम या न्यूनतम) खोजना होता है। इस अध्याय में हम दैनिक जीवन की समस्याओं का गणितीय सूत्रीकरण तथा उनका हल आलेखीय विधि से ज्ञात करने का प्रयास करेंगे
रैखिक प्रोग्रामन समस्या का गणितीय सूत्रीकरण
रैखिक प्रोग्रामन के गणितीय सूत्रीकरण को एक उदाहरण से समझने का प्रयास करते हैं
माना,
एक व्यवसायिक कंपनी क्रिकेट का सामान (बैट तथा बॉल) बेचती है। निवेश के लिए उसके पास Rs 40,000 हैं और वह अधिकतम 50 सामान ले सकता है। एक बैट पर Rs 2000 और एक बॉल पर Rs 500 की लागत आती है। वह अनुमान लगाता हैं कि एक बैट को बेचकर वह Rs 200 और एक बॉल को बेचने से Rs 50 का लाभ कमा सकता है। मान लीजिए कि वह सभी वस्तुओं को बेच सकता हैं जिनको कि वह खरीदता है, तब वह जानना चाहता हैं कि कितनी बैट एवं बॉल को खरीदना चाहिए ताकि उपलब्ध निवेश अधिकतम लाभ दें।
समस्या का गणितीय सूत्रीकरण
माना,
बैट की सँख्या =x
बॉल की सँख्या =y
जहाँ x≥0, y≥0
चूँकि अधिकतम 40000 रुपये निवेश किया जा सकता है
अतः 200x+50y≤40000
⇒4x+y≤800.....(i)
तथा अधिकतम 50 सामान लिया जा सकता है
अतः x+y≤50.....(ii)
यहाँ समी (i) व (ii) व्यवरोध कहलाते है।
यहाँ व्यवरोध से तात्पर्य एक रैखिक प्रोग्रामन समस्या के चरों पर रैखिक असमिकाये/समीकरण/प्रतिबंध, व्यवरोध कहलाते हैं। प्रतिबंध x≥0, y≥0 ऋणेत्तर व्यवरोध कहलाते हैं।
समस्या व्यवरोधों का व्यापक रूप निम्न होता है
ax+by≤ या ≥ या =c
यहाँ प्राप्त होने वाले लाभ को निम्न प्रकार से दर्शा सकते है
Z=200x+50y
लाभ का अधिकतम या न्यूनतम मान का यहाँ से गणना किया जा सकता है।
उक्त फलन उद्देश फलन कहलाता हैं जिसका व्यापक रूप
Z=ax+by
उद्देश्य फलन द्वारा चरों के विशेष मान के लिए अधिकतम या न्यूनतम मान ज्ञात किये जा सकते है। यहाँ चरों के मान ज्ञात करने के लिए आलेखीय विधि का प्रयोग किया जाता है।
अतः रैखिक प्रोग्रामन समस्या वह समस्या हैं जो कि x और y जैसे कुछ अनेक चरों के एक रैखिक फलन Z का इष्टतम मान (अधिकतम या न्यूनतम मान) ज्ञात करने से संबंधित है। प्रतिबंध यह हैं कि चर ऋणेतर पूर्णांक हैं और ये रैखिक असमिकाओं के समुच्चय रैखिक व्यवरोधों को संतुष्ट करते हैं। रैखिक पद से तात्पर्य हैं कि समस्या में सभी गणितीय संबंध रैखिक हैं जबकि प्रोग्रामन से तात्पर्य हैं कि विशेष प्रोग्राम या विशेष क्रिया योजना ज्ञात करना।
OMR (One Minute Revision)
रैखिक प्रोग्रामिंग को हल करने के लिए प्रमेय
प्रमेय 1: मान लीजिए रैखिक प्रोग्रामन समस्या के लिए, R एक सुसंगत क्षेत्र हैं और z=ax+by उद्देश्य फलन है। जब z का इष्टतम मान (अधिकतम या न्यूनतम) हो, जहां चर x और y रैखिक असमानताओं द्वारा वर्णित व्यवरोधों के अधीन हों। यह इष्टतम मान सुसंगत क्षेत्र के एक कोने बिंदु (शीर्ष) पर होना चाहिए।
नोट: एक सुसंगत क्षेत्र का एक कोना बिंदु उस क्षेत्र का एक बिंदु हैं जो दो सीमा रेखाओं का प्रतिच्छेदन है
प्रमेय 2: मान लीजिए कि रैखिक प्रोग्रामन समस्या के लिए, R एक सुसंगत क्षेत्र हैं और z=ax+by उद्देश्य फलन है। यदि R परिबद्ध है, तो z का R पर अधिकतम और न्यूनतम दोनों मान हैं और इनमें से प्रत्येक R के कोनीय बिंदु पर स्थित होता है
नोट: यदि सुसंगत क्षेत्र अपरिबद्ध हैं, तब उद्देश्य फलन के अधिकतम या न्यूनतम का अस्तित्व नहीं होता हैं
रैखिक प्रोग्रामन समस्या को हल करने की आलेखीय विधि
(Graphical Method of Solving Linear Programming Problems)
आलेखीय विधि से हल ज्ञात करने के लिए कोनीय बिंदु विधि का प्रयोग किया जाता है, आइए इसे समझने का प्रयास करते है
कोनीय बिंदु विधि (Corner Point Method)
कोनीय बिंदु विधि की कार्यविधि निम्नलिखित हैं
1. रैखिक प्रोग्रामन समस्या का गणितीय निरूपण कीजिए।
2. सभी व्यवरोधों को संगत सरल रेखा के समीकरण के रूप में लिखिए।
(4x+y≤800
x+y≤50
ऋणेत्तर व्यवरोध x≥0, y≥0)
3. समतल (ग्राफ) में सरल रेखाओं और ऋणेत्तर व्यवरोधों का आलेखन कीजिए।
जैसा की हमनें रैखिक असमिकाओं के लिए देखा था, सर्वप्रथम असमिकाओं को समीकरण के रूप में लिखेंगे तथा x−अक्ष (y = 0) व y−अक्ष (x = 0) पर बिंदु ज्ञात करेंगे। जिससे समीकरण का आलेख ज्ञात होगा तथा उन असमिकाओं में मूल बिंदु (0,0) के मान रखकर देखेंगे तथा असमिका के संतुष्टता के आधार पर हल क्षेत्र ज्ञात करेंगे। जैसे की नीचे आलेख में दर्शाया गया है।
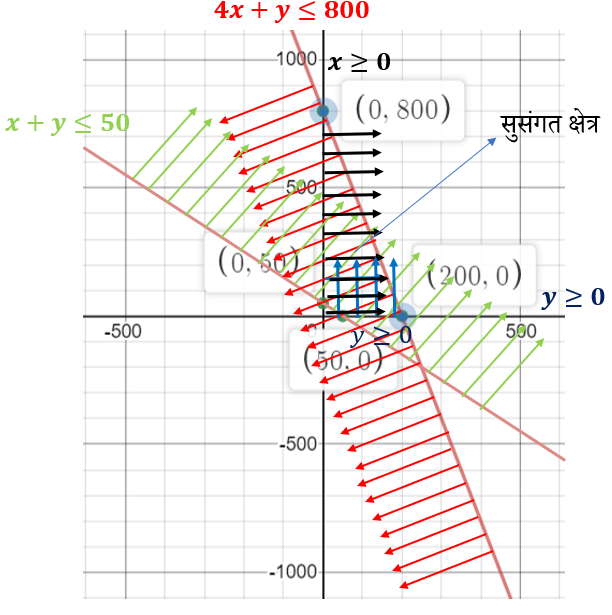
4. रैखिक प्रोग्रामन समस्या का सुसंगत क्षेत्र ज्ञात कीजिए।
(प्राप्त व्यवरोधों के लिए हल के अर्धतल ज्ञात करेंगे तथा इन व्यवरोधों के सम्मिलित हल अर्थात ऐसे हल जो सभी व्यवरोधों को संतुष्ट करें, सुसंगत हल होगा तथा प्राप्त हल क्षेत्र सुसंगत क्षेत्र कहलाएगा।)
5. सुसंगत क्षेत्र के प्रत्येक कोनीय बिंदु के निर्देशांक ज्ञात कीजिए जो दो रेखाओं का प्रतिच्छेदन बिंदु है।
(कोनीय बिंदु (50, 0), (200, 0), (0, 800), (0, 50))
6. प्रत्येक कोनीय बिंदु पर उद्देश्य फलन Z=ax+by का मान ज्ञात कीजिए। मान लीजिए इन बिन्दुओं पर अधिकतम और न्यूनतम मान क्रमशः M तथा m हैं।
7. यदि सुसंगत क्षेत्र परिबद्ध हैं अर्थात घिरा हुआ है, तो M और m क्रमशः उद्देश्य फलन के अधिकतम तथा न्यूनतम मान हैं।
(50, 0) के लिए
Z=200×50+50×0=10000
(200, 0) के लिए
Z=200×200+0×0=40000
(0, 800) Z=200×0+50×800=40000
(0, 50) Z=200×0+50×50=2500
यहाँ M=40000 तथा m=2500
सुसंगत क्षेत्र यदि परिबद्ध न हो तो निम्न प्रकार हल करेंगे
यदि सुसंगत क्षेत्र अपरिबद्ध है, तब
(i) उद्देश्य फलन का M अधिकतम मान हैं यदि ax+by>M के द्वारा निर्धारित खुला अर्धतल सुसंगत क्षेत्र के साथ कोई उभयनिष्ठ बिंदु नहीं रखता हैं अन्यथा उद्देश्य फलन का अधिकतम मान नहीं है।
(ii) उद्देश्य फलन का न्यूनतम मान m हैं यदि ax+by<m द्वारा निर्धारित खुला अर्धतल सुसंगत क्षेत्र के साथ कोई उभयनिष्ठ बिंदु नहीं रखता हैं अन्यथा उद्देश्य फलन का कोई न्यूनतम मान नहीं है।
OMR (One Minute Revision)
कोनीय बिंदु विधि (Corner Point Method) को लागू करने के चरण (कार्यविधि )
(b) उद्देश्य फलन का न्यूनतम मान m हैं यदि ax+by<m द्वारा निर्धारित खुला अर्धतल सुसंगत क्षेत्र के साथ कोई उभयनिष्ठ बिंदु नहीं रखता हैं अन्यथा उद्देश्य फलन का कोई न्यूनतम मान नहीं है।
उदाहरण 1
निम्नलिखित रैखिक प्रोग्रामन समस्या का आलेखीय विधि से हल करें।
न्यूनतमीकरण करें
z=x−7y+190
जबकि
x+y≤8
x≤5
y≤5
x+y≥4
x≥0,y≥0
सर्वप्रथम हम निम्नलिखित रेखाओं का आलेख खींचते हैं
x+y=8…..(1)
x=5…….(2)
y=5…..(3)
x+y=4……(4)
हल क्षेत्र-
x+y≤8 में मूलबिंदु (0,0) रखने पर
0≤8 अतः संतुष्ट करता है, इसलिए निचला अर्धतल हल क्षेत्र होगा।
x+y≥4 में मूलबिंदु (0,0)रखने पर
0≥4 अतः संतुष्ट नहीं करता है, इसलिए ऊपरी अर्धतल हल क्षेत्र होगा।
इसी प्रकार,
x≤5 का बायाँ भाग तथा y≤5 का निचला भाग हल क्षेत्र होगा।
अतः इनके उभयनिष्ठ हल क्षेत्र आलेख में देख सकते हैं जो की सुसंगत हल क्षेत्र है।
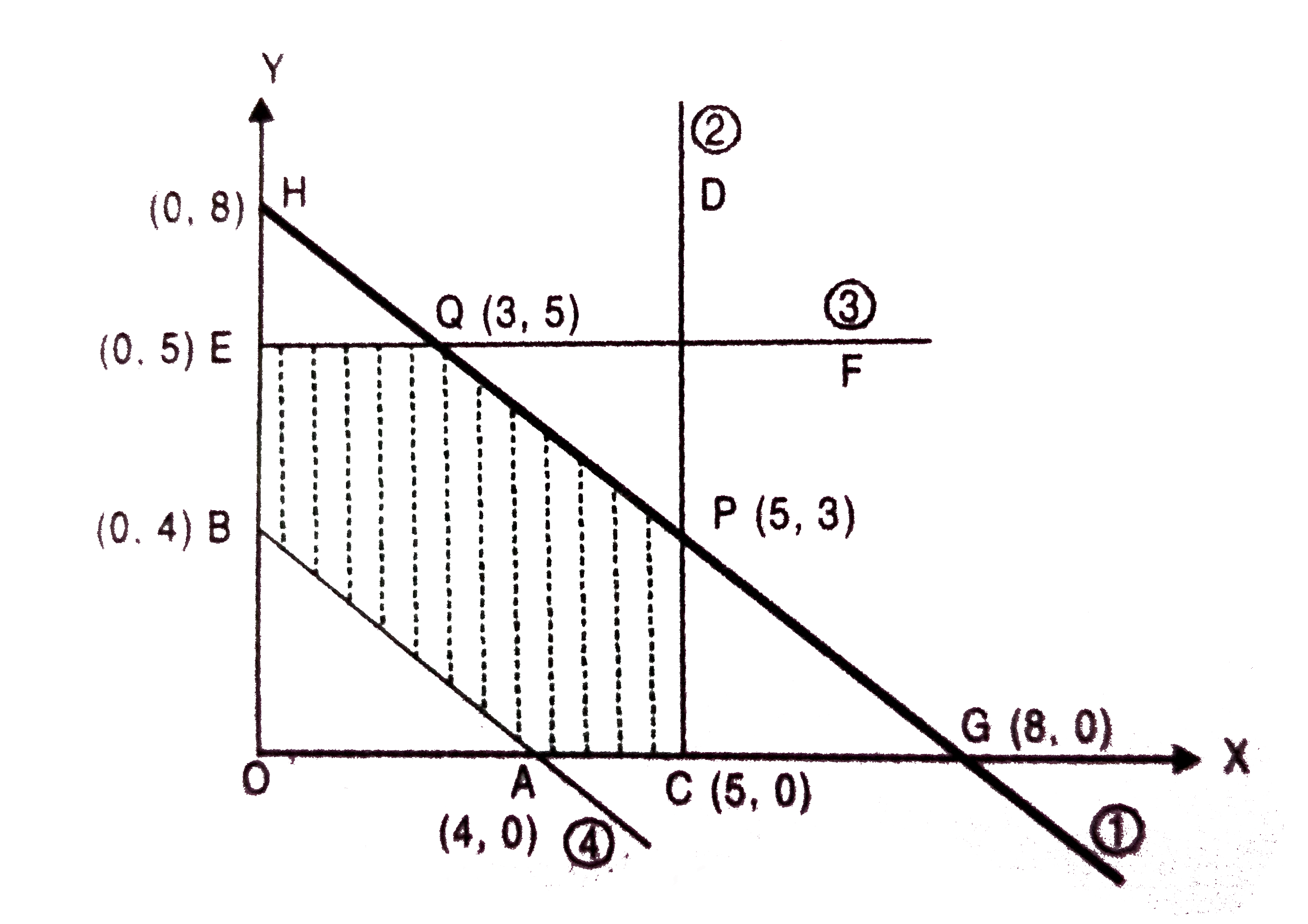
छायांकित क्षेत्र ACPQEBA सुसंगत क्षेत्र हैं जो कि परिबद्ध हैं। इसके शीर्ष A(4,0) ,C(5,0), P(5,3), Q(3,5) तथा E(0,5), B(0,4) है।
दिया है,
z=x−7y+190
A(4,0) पर z=194
C(5,0), पर, z=195
P(5,3) पर, z=174
Q(3,5) पर,z=158
E(0,5) पर, z=155
B(0,4) पर,z=162
स्पष्टतः Z, E(0,5) पर न्यनूतम हैं तथा Z का यह न्यूनतम मान 155 है।
उदाहरण 2
निम्नलिखित रैखिक प्रोग्रामन समस्या का हल आलेखीय विधि से करें।
न्यूनतमीकरण करें
z=3x+5y
जबकि
x+y≥2
x+3y≥3
x,y≥0
सर्वप्रथम हम निम्नलिखित रेखाओं का आलेख खींचते हैं
x+y=2……(1)
तथा x+3y=3……(2)
ये रेखाएं P(32,12) पर प्रतिच्छेद करती है।
साथ ही दोनों असमिकाओं में ऊपरी अर्धतल हल क्षेत्र होगा।
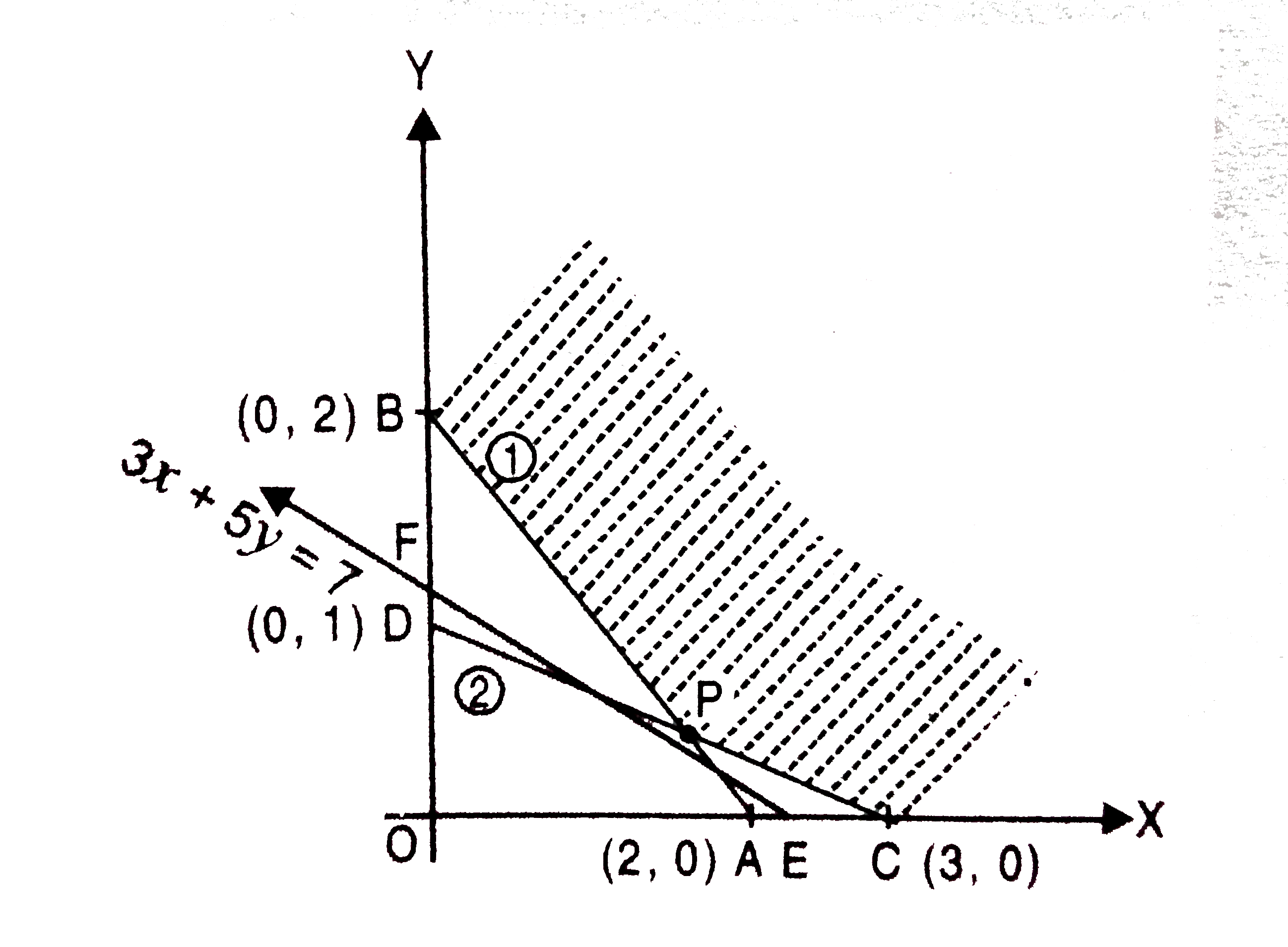
छायांकित क्षेत्र सुसंगत क्षेत्र है, स्पष्टतः सुसंगत क्षेत्र अपरिमित है।
सुसंगत क्षेत्र के शीर्ष C(3,0), P(32,12) तथा B(0,2) हैं।
दिया है,
z=3x+5y
C(3,0) पर, z=9
P(32,12) पर, z=92+52=7 (न्यूनतम)
B(0,2) पर,z=10
यहाँ असमिका 3x+5y<7 के संगत क्षेत्र का कोई बिंदु सुसंगत क्षेत्र में उभयनिष्ठ नहीं हैं। चूँकि मूलबिंदु (0,0) का मान रखने पर 0<7 संतुष्ट करता है, अतः निचला अर्धतल हल क्षेत्र होगा।
अतः न्यूनतम मान m=7 है। (अपरिबद्ध सुसंगत क्षेत्र की स्थिति मे)
∴Z=3x+5y का मान P(32,12) पर न्यूनतम है।
Z का न्यूनतम मान =7
उदाहरण 3
अधिकतमीकरण करें
Z=2x+3y
जबकि
x+y≤1,
x+y≥3,
x≥0,y≥0
सर्वप्रथम हम निम्नलिखित रेखाओं का आलेख खींचते हैं।
x+y=1 तथा x+y=3
असमिकाओं x+y≤1 (निचला अर्धतल) तथा x+y≥3 (ऊपरी अर्धतल) को निरूपित करने वाले क्षेत्र छायांकित हैं।
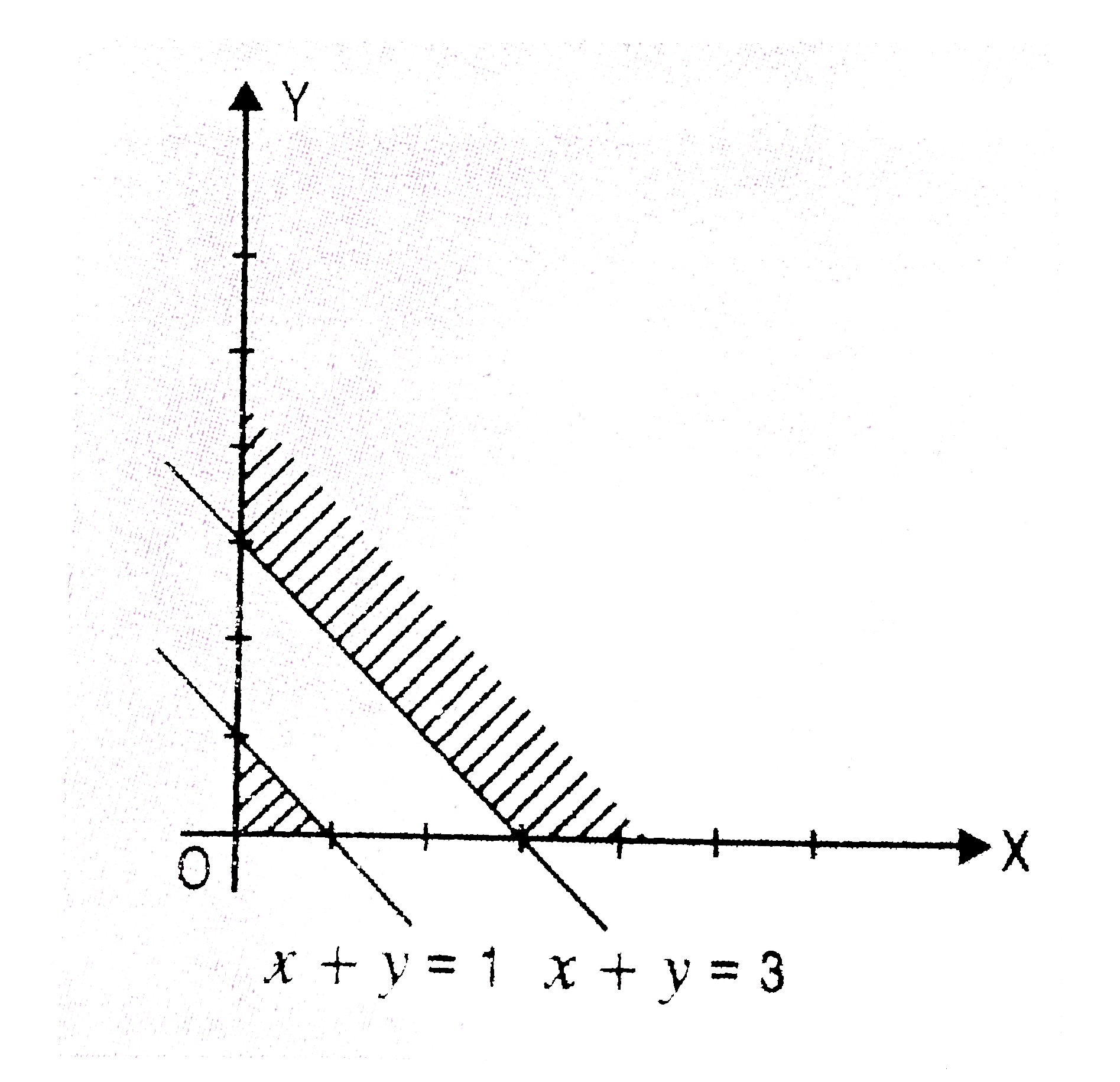
यहां हम देखते हैं कि दिए गए व्यवरोधों को संतुष्ट करता हुआ कोई उभयनिष्ठ बिंदु नहीं है। अतः Z का अधिकतम मान संभव नहीं है।
उदाहरण 4
एक निर्माता दो सामान A और B बनाता है। सामान A, 200 रू0 प्रति इकाई की दर से बिकती हैं और निर्माण में 30 मिनट लगते हैं। सामान B, 300 रू0 प्रति इकाई की दर से बिकती हैं और निर्माण में 1 घंटा लगते हैं। A की 14 इकाई और B की 16 इकाई के लिए मांग है। एक सप्ताह में 40 घंटे निर्माण कार्य होता हैं एवं साप्ताहिक टर्न-ओवर 10000 रू0 से कम नहीं होना है। यदि A के प्रत्येक नग पर लाभ 20 रू0 एवं B के प्रत्येक नग पर लाभ 30 रू0 हो तो प्रत्येक के कितने नगों का निर्माण किया जाए कि लाभ अधिकतम हो? समस्या का हल आलेखीय विधि से निकालें।
माना कि,
उत्पाद A तथा B के क्रमशः x और y इकाई उत्पादित किए जाते हैं तथा कुल लाभ Z है, तो x और y निम्नलिखित शर्तों को संतुष्ट करेंगें।
200x+300y≥10,000
या 2x+3y≥100
12x+1.y≤40 (चूँकि 30 मिनट = 12 घंटा)
या x+2y≤80
x≥14
y≥16
x,y≥0,
रैखिक प्रोग्रामन समस्या का गणितीय रूप निम्नलिखित होगा:
अधिकतमीकरण करें
z=20x+30y (लाभ)
जबकि
2x+3y≥100
x+2y≤80
x≥14
y≥16
x≥0,y≥0
अब हम निम्नलिखित रेखाओं का आलेख खींचते हैं
2x+3y=100…..(1)
x+2y=80…(2)
x=14…….(3)
y=16…. (4)
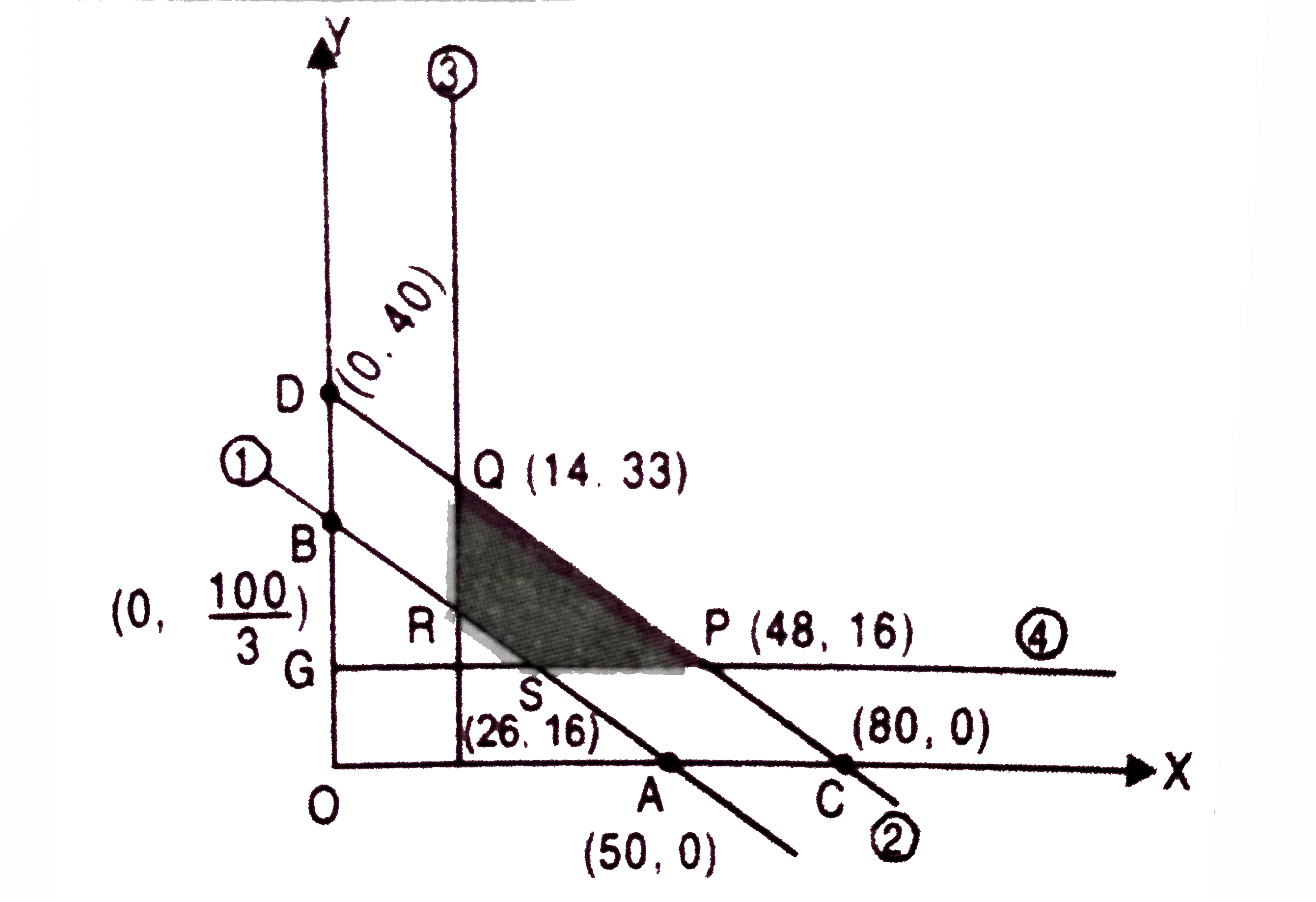
सुसंगत क्षेत्र SPQR हैं जो परिबद्ध है।
सुसंगत क्षेत्र का शीर्ष
S(26,16), P(48,16) Q(14,33) तथा R(14,24) है।
दिया है,
z=20x+30y
अतः S(26,16) पर z=1000
P(48,16) पर,z=1440
Q(14,33) पर,z=1270
R(14,24) पर,z=1000
अतः महत्तम लाभ 1440 रू0 हैं तथा इसके लिए उत्पाद A का 48 इकाई और उत्पाद B का 16 इकाई उत्पादित करना होगा।
महत्वपूर्ण बिन्दु
कोनीय बिंदु विधि (Corner Point Method) को लागू करने के चरण (कार्यविधि )
(b) उद्देश्य फलन का न्यूनतम मान m हैं यदि ax+by<m द्वारा निर्धारित खुला अर्धतल सुसंगत क्षेत्र के साथ कोई उभयनिष्ठ बिंदु नहीं रखता हैं अन्यथा उद्देश्य फलन का कोई न्यूनतम मान नहीं है।