JEE Type Solved Examples: Single Matching Type Questions from ARIHANT MATHS (ENGLISH) PERMUTATIONS AND COMBINATIONS for Class 12
| Class 12 | MATHS |
| Chapter | PERMUTATIONS AND COMBINATIONS |
| ARIHANT MATHS (ENGLISH) | JEE Type Solved Examples: Single Matching Type Questions |
| Medium | English |
| Academic Year | 2023-2024 |
Question 118
A is a set containing n elements. A subset P1 of A is chosen. The set A is reconstructed by replacing the elements P Next, a of subset P2 of A is chosen and again the set is reconstructed by replacing the elements of P2, In this way, m subsets P1,P2....,Pm of A are chosen. The number of ways of choosing P1,P2,P3,P4...PmView SolutionQuestion 119
A is a set containing n elements. A subset P of A is chosen. The set A is reconstructed by replacing the elements of P. A subset of A is again chosen. Find the number of ways of choosing P and Q,
so that
(i) P∩Q contains exactly r elements.
(ii) P∩Q contains exactly 2 elements.
(iii) P∩Q=ϕView SolutionQuestion 138
All the letters of the word 'AGAIN' be arranged and the words thus formed are known as 'Simple Words'. Further two new types of words are defined as follows:
(i) Smart word: all the letters of the word 'AGAIN' are being used, but vowels can be repeated as many times as we need.
(ii) Dull word: All the letters of the word 'AGAIN' are being used, but consonants can be repeated as many times as we need.
Q. Number of 7 letter smart words is a. 1500 b. 1050 c. 1005 d. 150View SolutionQuestion 139
All the letters of the word 'AGAIN' be arranged and the words thus formed are known as 'Simple Words'. Further two new types of words are defined as follows:
(i) Smart word: all the letters of the word 'AGAIN' are being used, but vowels can be repeated as many times as we need.
(ii) Dull word: All the letters of the word 'AGAIN' are being used, but consonants can be repeated as many times as we need.
Q. Number of 7 letter dull words in which no two vowels are together, is a. 402 b. 420 c. 840 d. 42View SolutionQuestion 156
Seven relatives of a man comprises four ladies and three gentlemen: his wife has also seven relatives-three of them are ladies and four gentlemen. In how many ways fan they invite 3 ladies and 3 gentlemen at a dinner party so that there are three mans relatives and three wifes relatives?View SolutionQuestion 163
There are n straight lines in a plane such that n1 of them are parallel in onne direction, n2 are parallel in different direction and so on, nk are parallel in another direction such that n1+n2+..+nk=n. Also, no three of the given lines meet at a point. prove that the total number of points of intersection is 12{n2−k∑r=1n2r}.View SolutionQuestion 166
There are 2n guests at a dinner party. Supposing that eh master and mistress of the house have fixed seats opposite one another and that there are two specified guests who must not be placed next to one another, show that the number of ways in which the company can be placed is (2n−2!)×(4n2−6n+4).View Solution
All Exercises from ARIHANT MATHS (ENGLISH) Class 12 MATHS PERMUTATIONS AND COMBINATIONS
- EXERCISE FOR SESSION 1
- EXERCISE FOR SESSION 2
- EXERCISE FOR SESSION 3
- EXERCISE FOR SESSION 4
- EXERCISE FOR SESSION 5
- EXERCISE FOR SESSION 6
- EXERCISE FOR SESSION 7
- EXERCISE (SINGLE OPTION CORRECT TYPE QUESTIONS)
- EXERCISE (MORE THAN ONE CORRECT OPTION TYPE QUESTIONS)
- EXERCISE (PASSAGE BASED QUESTIONS)
- EXERCISE (SINGLE INTEGER ANSWER TYPE QUESTIONS)
- EXERCISE (MATCHING TYPE QUESTIONS)
- PERMUTATIONS AND COMBINATIONS EXERCISE 5: MATCHING TYPE QUESTIONS
- EXERCISE (STATEMENT I AND II TYPE QUESTIONS)
- EXERCISE (SUBJECTIVE TYPE QUESTIONS)
- EXERCISE (QUESTIONS ASKED IN PREVIOUS 13 YEARS EXAM)
- EXAMPLES
- JEE TYPE SOLVED EXAMPLES: SINGLE MATCHING TYPE QUESTIONS



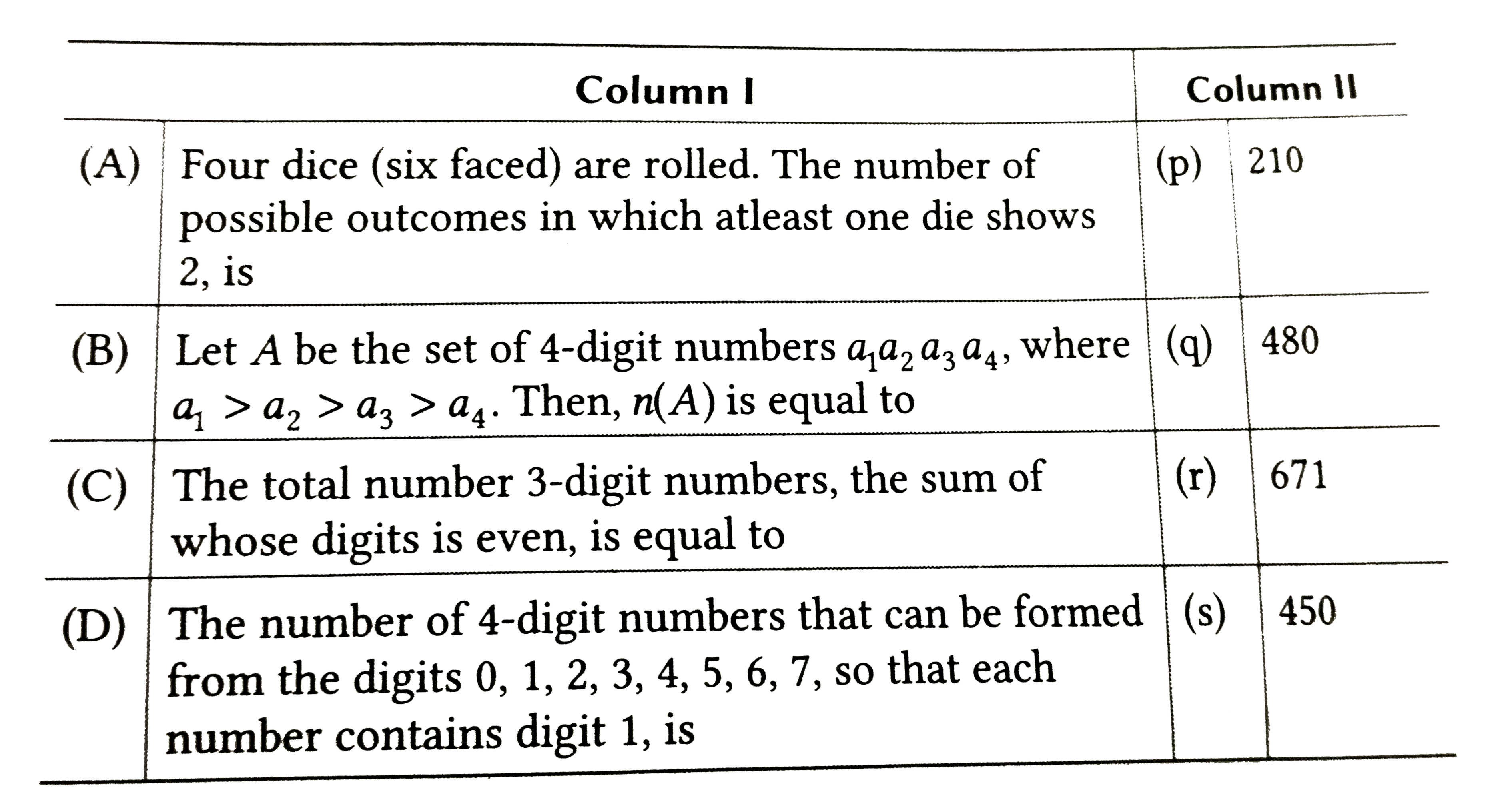 .
.