ELLIPSE for Class 12 MATHS
Introduction
Hello Students, In today's class we will learn a very interesting topic which is Ellipse which has a good weightage in the exam of JEE.
These notes are designed keeping in mind the basics and the recent changes in the syllabus and pattern of JEE.
You can follow Doubtnut for all the videos related to JEE 2022.
The ellipse is one of the four classic conic sections that is generally created by slicing a cone with a plane. The other conic sections are the parabola, the circle, and the hyperbola. The ellipse is a very important concept in astronomy as celestial objects in periodic orbits around other celestial objects all trace out the conic section known as ellipses.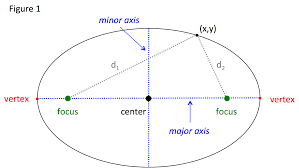
Index
Definition and Basic terms related to ellipse|Standard equation of ellipse|Tracing of an ellipse|Facts about an Ellipse|Focal distance of a point|Two standard forms of ellipse|Comparision chart between Standard ellipse|To find the various parameter of an ellipse|Comparision chart between above two ellipse|Position of a point w.r.t ellipse|Tangents|Normals
Definition and Basic terms related to ellipse
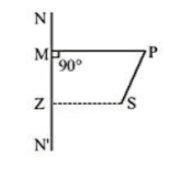
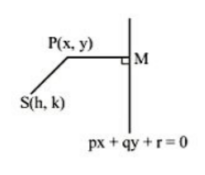
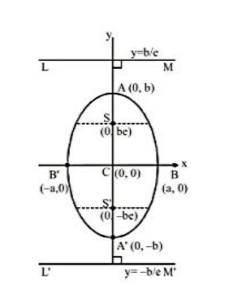
An ellipse is the locus of the point which moves in a plane such that the ratio of its distance from a fixed point (focus) to fixed straight line (directrix) is always constant (called eccentricity). In the given figure. S is the focus and NN’ is the directrix.
Let P be a point on the ellipse, then
PSPM=e,e<1 (for ellipse). Thus, we can find the equation of an ellipse when the coordinates of its focus, equation of the directrix and eccentricity (e) are given.
Let the equation of the ellipse be x2a2+y2b2=1....(1)
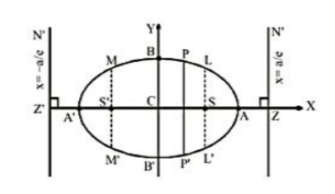
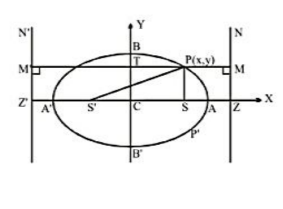
1. Centre :
In the figure, C is the center of the ellipse. All chords passing through C arc called diameter and bisected at C.
2.Foci:
S and S’ are the two foci of the ellipse and their coordinates are (ae,0) and (—ae,0) respectively. The line containing two foci arc called the focal axis and the distance between S & S’ the focal length
3. Directrices :
ZN and Z’N’ are the two directrices of the ellipse and their equations are x=ae and x=−ae respectively. Here Z and Z' are called foot of directrix.
4. Axes
The line segments A’A and B'B are called the major and minor axes respectively of the ellipse. The point of intersection of major and minor axis is called centre of the ellipse. Major and minor axis together are called principal axis of ellipse.
Here Semi-major axis are CA=CA’=a
and Semi-minor axis are CB=CB’=b
5. Vertex:
The points where major axis meet the ellipse is called its vertices. In the given figure. A’ and A are the vertices of the ellipse.
6. Ordinate and double ordinates :
Let P be a point on the ellipse. From P we draw PM perpendicular to major axis of the ellipse. Produce PM to meet the ellipse at F, then PM is called an ordinate and PMP’ is called the double ordinate of the
point P.
7. Latus rectum :
When double ordinate passes through focus then it is called the Latus rectum.Let L’L=2k. then LS=k so L=(ae,k).
Here LL and MM’ are called latus rectum.
8. Focal chord :
A chord of the ellipse passing through its focus is called a focal chord.
Standard equation of ellipse
Let S be the focus & ZM is the directrix of an ellipse. Draw perpendicular from S to the directrix which meet it at Z. A moving point is on the ellipse such that
PS=ePM
then there is point lies on the line SZ and which divide SZ internally at A and externally at A’ in the ratio of e:1.
therefore SA=eAZ.....(i)
SA=eA’Z...(ii)
Let AA’=2a & take C as mid point of AA’
∴CA=CA’=a
Add (i) & (ii)
SA+SA’=e(AZ+A’Z)
⇒AA’=c[CZ−CA+CA’+CZ]
2a=2eCZ
⇒CZ=ae....(iii)Subtract (ii) & (i), we get
SA’—SA=e(AZ—AZ)
⇒(CA’+CS)−(CA−CS)
=e[(CA’+CZ)−(CZ−−CA)]
⇒2CS=2eCA
CS=ae.....(iv)
Result (iii) & (iv) are independent of axis.
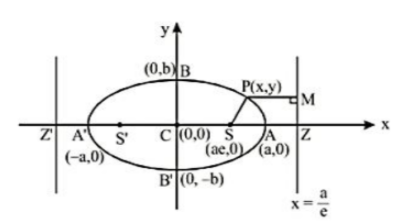
Consider CZ line as x-axis, Cas origin & perpendicular to this line & passes through C is considered as y-axis. Let P(x,y) is a moving point, then
By definition of ellipse.
PS=ePM⇒(PS)2=e2(PM)2
(x−ae)2+(y−0)2=e2((ae)−x)2
x2+a2e2−2xae+y2—a2+c2x2—2xae
You will get finally x2a2+y2b2=1
Tracing of an ellipse
Given ellipse is x2a2+y2b2=1...(1)
( 1 ) If we put y=0 then we see that ellipse cuts x-axis at (±a.0).
( ii )If we put x=0 then we see that ellipse cuts y-axis at (0,±b).
( iii ) Equation of ellipse does not change when y is replaced by −y. Hence, ellipse is symmetrical about x-axis. (Since equation contain even power of y therefore curve is symmetric about x-axis).
( iv ) When x is replaced by −x, the equation of curve does not change therefore ellipse is symmetrical about
y-axis. (Since equation contain even power of x therefore curve is symmetric about y-axis).
Facts about an Ellipse
( 1 ) By the symmetry of equation of ellipse, if we take second focus S’(−ae,0) & second directrix x=−ae & perform same calculation, we get same equation of ellipse. therefore there are two focii & two directrix of an ellipse. The two focii of ellipse are (ae,0) and (−ae,0) and the two corresponding directrices are lines x=ae and x=−ae. If focus of the ellipse is taken as (ae,0). then corresponding directrix is x=ae and if focus is (−ae,0), then corresponding directrix is x=ae and if focus (−ae,0), then the corresponding directrix is x=−ae.
( 2 ) If equation of directrix is px+uy+r=0 & focus is (h,k) then its equation will be
(PS)2=e2(PM)2
(X−h)2+(y−k)2=e2(px+q+r√p2+q2)2
( 3 )Distance between foci SS=2ae & distance between directrix Z’=2ae
( 4 )Degree of fIatness of an ellipse is also called on eccentricity & written as
e=CSCA= (Distance from centre of focus)/(Distance from centre to vertex)
If e→0⇒b→a⇒ focii becomes closer & move towards centre and ellipse becomes circle.
If e→1⇒b→0⇒ ellipse get thinner & thinner.
( 5 )
Two ellipse are said to be similar if they have same eccentricity.
( 6 ) Distance of focus from the extremity of minor axis is equal to a because a2e2+b2=a2
Focal distance of a point
Let P(x,y) be any point on the ellipse
x2a2+y2b2=1.....(1)
Then by definition of ellipse,
SP=ePM=e(MT−PT)=e((ae)−x)=a−ex
S’P=ePM’=e(M'T+PT)=e((ae)+X)=a+ex
Hence SP+S’P=2a
Because of the above property, ellipse is also defined as the locus of a point which moves in a plane such that the sum of its distance from two fixed points (called foci) is a constant (Length of major axis). This definition is called the physical definition of the ellipse.
Hence PS+PS’=QS+QS’=TS+TS’= length of major axis
Two standard forms of ellipse
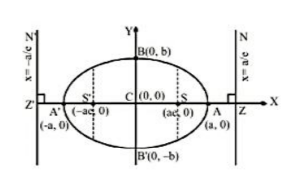
There are two standard forms of ellipse with centre at the origin and axes along coordinate axes. The foci of the ellipse are either on the x-axis or on the y-axis.
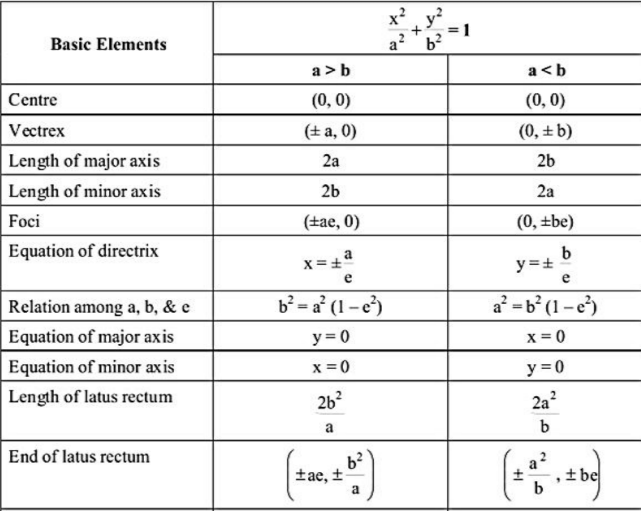
1. Major axis along x-axis :
The equation of this type of ellipse is of the form (x2a2)+(y2b2)=1 , where a>b>0 and b=a√1−e2
For this ellipse:
(i) Major axis is 2a
(ii) Minor axis is 2b.
(iii) Centre is (0,0)
(iv) Vertices are (±a.0)
(v) Foci are (±ae,0)
(vi) Equation of directrices are x=±ae
(vii) Equation of major axis is y=0
(viii) Equation of minor axis is x=0
(ix) Length of latus rectum =2b2a
(x) Extremity of latus rectum is (±ae,±b2a)
2. Major axis along y-axis :
The equation of this type of ellipse is of the form (x2a2)+(y2b2)=1 , where b>a>0 and a=b√1−e2
For this ellipse:
(i) Major axis is 2b
(ii) Minor axis is 2a.
(iii) Centre is (0,0)
(iv) Vertices are (0,±b)
(v) Foci are (0,±be)
(vi) Equation of directrices are y=±be
(vii) Equation of major axis is x=0
(viii) Equation of minor axis is y=0
(ix) Length of latus rectum =2a2b
(x) Extremity of latus rectum is (±a2b,±be)
Comparision chart between Standard ellipse
To find the various parameter of an ellipse
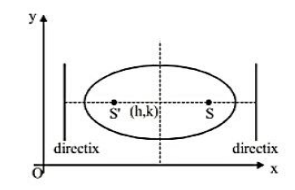
Equation of an ellipse whose axis are parallel to coordinate axis and its centre is (h,k). The foci of the ellipse are either on x-axis or on the y-axis.
Major axis parallel to x-axis
Here the equation of ellipse is of the form (x−h)2a2+(y−k)2b2=1 where a>b & b2=a2(1−e2)
Here the equation of the ellipse is of the form (X2a2)+(Y2b2)=1, where X=x−h and Y=y−k.
( 1 ) Equation of major axis is Y=0, i.e., y−k=0
Equation of minor axis is X=0, i.e., x−h=0
( 2 )Coordinate of centre of the ellipse are given by :
X=0 and Y=0 i.e. x−h=0 and y−k=0
Centre of the ellipse is (h,k)
( 3 ) Coordinate of foci of the ellipse are given by
X=±ae,Y=0 i.e., x−h=±ae and y−k=0
:. Hence foci of the ellipse are (h±ae,k)
( 4 ) Equation of the directrices of the ellipse are X=±ae , i.e., x−h=±ae
Thus directrices are x=h±ae
( 5 )Coordinate of ends of latera recta are given by X=±ae,Y=±b2a i.e. x−h=±ae,y−k=±b2a
Therefore ends of latera recta are given by (h±ae,k±b2a)
( 6 ) Coordinate of vertices of the ellipse are given by X=±a,Y=0 i.e., x—h=±a,y—k0. Hence vertices are (h±a,k)
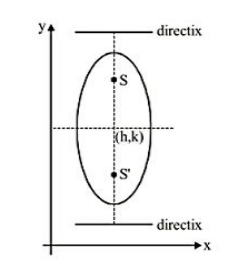
( II ) Major axis parallel to y-axis :
Here the equation of ellipse is of the form (x−h)2a2+(y−k)2b2=1 where a<b & a2=b2(1−e2)
Here the equation of the ellipse is of the form (X2a2)+(Y2b2)=1, where X=x—h and Y=y−k.
( 1 ) Equation of major axis is X=0, i.e., x−h=0
Equation of minor axis is Y=0, i.e., y−k=0
( 2 )
Coordinate of centre of the ellipse are given by :
X=0 and Y=0 i.e. x−h=0 and y−k=0
Centre of the ellipse is (h,k)
( 3 ) Coordinate of foci of the ellipse are given by
X=0,Y=±be i.e., x−h=0 and y−k=±be
:. Hence foci of the ellipse are (h,k±be)
( 4 )
Equation of the directrices of the ellipse are Y=±be , i.e., y−k=±be
Thus directrices are y=k±be
( 5 )
Coordinate of ends of latera recta are given by X=±a2b ,Y=±ae i.e. x−h=±a2b,y−k=±be
( 6 ) Coordinate of vertices of the ellipse are given by X=0,Y=±b i.e., x−h=0,y−k=±b. Hence vertices are (h,k±b)
Comparision chart between above two ellipse
Example 1
Find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.x216+y29=1
Given equation is x216+y29=1.
This is of the form x2a2+y2b2=1, where a2>b2.
So, it is an equation of a horizontal ellipse.
Now, (a2=16andb2=9⇒(a=4andb=3).
∴C=√a2−b2=√16−9=√7.
Thus, a=4,b=3andc=√7.
(i) Length of the major axis =2a=(2×4) units = 8 units.
Length of the minor axis = 2b=(2×3) units = 6 units.
(ii) Coordinates of the vertices are A(−a,0)andB(a,0),i.e.,A(−4,0)andB(4,0).
(iii) Coordinates of the foci are F1(−c,0)andF2(c,0),i.e.,F1(−√7,0)andF2(√7,0).
(iv) Eccentricity , e=ca=√74.
(v) Length of the latus rectum = 2b2a=(2×9)3 units =92 units.
Example 2
Find the lengths of the major and minor axes, coordinates of the vertices and the foci, the eccentricity and length of the latus rectum of the ellipse:
x24+y236=1.
Given equation is x24+y236=1.
This is of the form x2b2+y2a2=1, where a2>b2.
So, it is an equation of a vertical ellipse.
Now, (b2=4anda2=36)⇒(b=2anda=6).
∴c=√a2−b2=√36−4=√32=4√2.
Thus, a=6,b=2andc=4√2.
(i) Length of the major axis = 2a=(2×6) units = 12 units.
Length of the minor axis = 2b=(2×2) units = 4 units.
(ii) Coordinates of its vertices are A(0, -a) and B(0,a), i.e., A(0, -6) and B(0, 6).
(iii) Coordinates of its foci are F1(0,−c)andF2(0,c),i.e.,F1(0,−4)√2)andF2(0,4√2).
(iv) Eccentricity, e=ca=4√26=2√23.
(v) Length of the latus rectum = 2b2a=(2×4)6 units =43 units.
Example 3
Find the equation if the ellipse whose axes are along the coordinate axes, vertices are(±5,0) and foci at (±4,−0).
Since the equation of the ellipse be x2a2+y2b2=1, where a2>b2.
Its vertices are (±a,0) and therefore, a = 5.
Its foci are (±c,0) and therefore, c = 4.
∴C2=(a2−b2)⇒b2=(a2−c2)=(25−16)=9.
Thus, a2=52=25andb2=9.
Hence, the required equation is x225+y29=1.
Example 4
Find the eccentricity coordinates of foci length of the latus rectum of the following ellipse: 4x2=9y2=1
Given equation is x2(1/4)+y2(1/9)=1.
∴A2=14,b2=19andc2=(a2−b2)=(14−19)=536.
∴A=12,b=13andc=√56.
Example 5
The ends of 20 cm long rod moves on two mutually perpendicular lines. If a point on this rod at 4 cm distance from end then from the eccentricity of the ellipse formed by moving that point.

Let the length of rod AB=20cm which moves on two mutually perpendicular lines OX and OY. Let point P(x,y) be at a didtance of 4 cm from end A.
∴ PB=AB-AP=20-4=16cm
Let PM and PN are perpendiculars from p to x-axis and y-axis respectively.
∴ PM=yandPN−x
Let ∠PAM=θ ⇒ ∠BPN=θ
in ΔAPM,sinθ=y4andinΔBPN,cosθ=x16
Now cos2θ+sin2=1
⇒x2162+y242=1, which is the equation of the ellipse.
Here a=16 and b=4
∴ b2=a2(1−e2)
From 16=256(1−e2)
⇒ 1−e2=116
⇒ e2=1516
⇒ e=√154.
Position of a point w.r.t ellipse
Let S(x,y)=(x2a2)+(y2b2) be the given ellipse and P(x1,y1) is the given point.
( i )If S(x1,y1)>0 then P(x1,y1) lie outside the ellipse.
( ii )If S(x1,y1)<0 then P(x1,y1) lie inside the ellipse.
( iii )If S(x1,y1)=0 then P(x1,y1) lie on the ellipse. This result holds true for circle and parabola also.
Tangents
( 1 ) Point form :x⋅x1a2+yy1b2=1 is tangent to the ellipse at (x1y1).
Since point (x1,y1) lie on the curve therefore we can use standard substitution to obtain the equation of tangent.
( ii ) Slope form :
Let the given line is y=mx+c and given ellipse is x2a2+y2b2=1.
If line touch is the ellipse then by solving the two equations simultaneously (by eliminating y from above equations we get x2a2+(mx+c)2b2=1
i.e. (b2+a2m2)x2+2a2cmx+a2(c2−b2)=0.....(3)
Since line is tangent to the ellipse therefore its D=0
4a4c2m2−4(b2+a2m2)⋅a2(c2−b2)=0
or b2(−c2+b2+a2m2)=0
or c2=b2+a2m2 or c=±√a2m2−b2 which is the required condition of tangency.
Substituting this value of e in y=mx+c, we have y=mx+√a2m2+b2 or y=mx−√a2m2+b2, which are tangents to the ellipse for all values of m.
Here ± sign represents two tangents to the ellipse having the same m, i.e. there are two tangents parallel to any given direction.
The equation of any tangent to the ellipse (x−h)2a2+(y−b)2b2=1
(y−k)=m(x−h)±√a2m2+b2
( iii ) Parametric form :
xcos(θ)a+ysin(θ)b=1 is tangent to the ellipse at the point (acos(θ),bsin(θ)).
NOTE:
( 1 ) Point of intersection of the tangents at the point α,β is ⎛⎜⎝acos(α+β)2cos(α−β)2,asin(α+β)2sin(α−β)2⎞⎟⎠ can be deduced by comparing chord joining P(α) and Q(β) with C.O.C. of the pair of tangents from R(x1,y1) on the ellipse, where
x=acos(α+β)2cos(α−β)2 and y=asin(α+β)2sin(α−β)2
( ii ) The eccentric angles of point of contact of two parallel tangents differ by it. Conversely if the difference between the eccentric angles of two points is it then the tangents at these points are parallel.
Example 5
An ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is (A) √3 (B) 2 (C) 2√2 (D) √5
Given ellipse
x225+y216=1
∴E2=1−1625ore=35
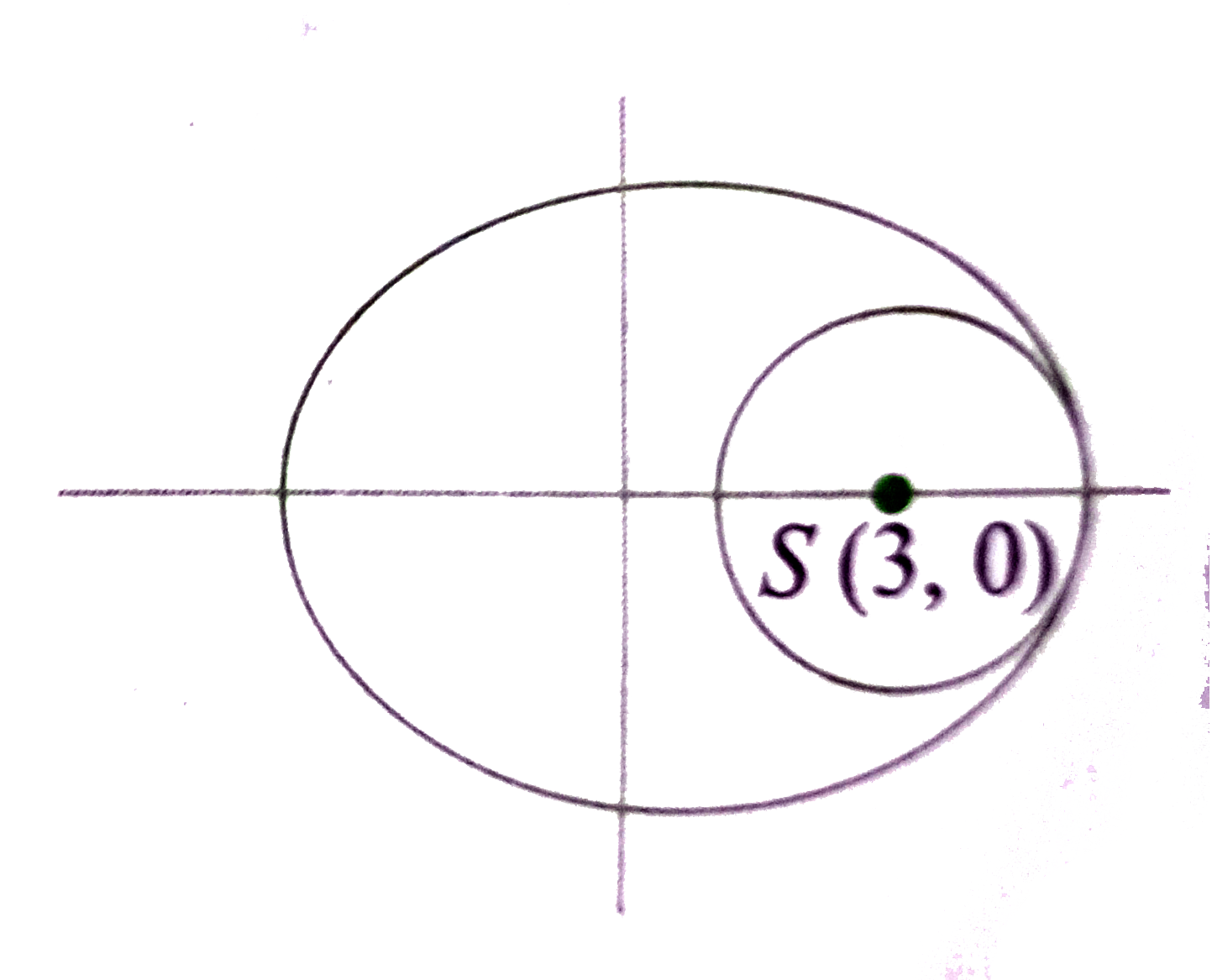
then foci are (±ae,0)≡(±3,0)
Now, the circle having center (3,0) is
(x−3)2+y2=r2
Eliminating y2 from (1) and (2), we get
16x2+25r2−25(x2−6x+9)=400
or −9x2+150x+25r2−625=0
since the circle touches the ellipse, the above equation, has equal roots. Hence D=0,i.e.,22500+36(25r2−625)=0, which is not possible
Then the circle will touche the ellipse at the end of the major axis, (5,0) Hence, the radius is 2
Example 6
A tangent having slope of −43 to the ellipse x218+y232=1 intersects the major and minor axes at points AandB,respectively. If C is the center of the ellipse, then find area of triangle ABC.
For a given ellipse, the equation of tangent whsoe slope is m is y=mx+√18m2+32
For m=-4/3, the tangent is
y=−43×√18(169)+32
=−43x+18
or 4x+3y=24
This intersects the amjor and minor axes at (6,0) and B(0,8), respectively.
Example 7
Find the slope of a common tangent to the ellipse x2a2+y2b2=1 and a concentric circle of radius r.
The equation of any tangent to the given ellipse is y=mx+√a2m2+b2
If it touches x2+y2=r2, then
√a2m2+b2=r√1+m2
or m2(a2−r2)=r2−b2
or m=√r2−b2a2−r2
Example 8
If the tangent at any point of the ellipse x2a3+y2b2=1 makes an angle α with the major axis and an angle β with the focal radius of the point of contact, then show that the eccentricity of the ellipse is given by e=cosβcosα
LetP(acosθ,bsinθ) be any point on the ellipse.
The equation of tangent at P(θ) is
xcosθ4+(ysinθ)(b()=1 (1)
Tangent meets the major axis at T(asecθ,0).
Applying since rule in ΔPST, we get
PSsin(π−α)=STsinβ
or1−ecosθsinα=a(secθ−e)sinβ
or cosθ=sinαsinβ 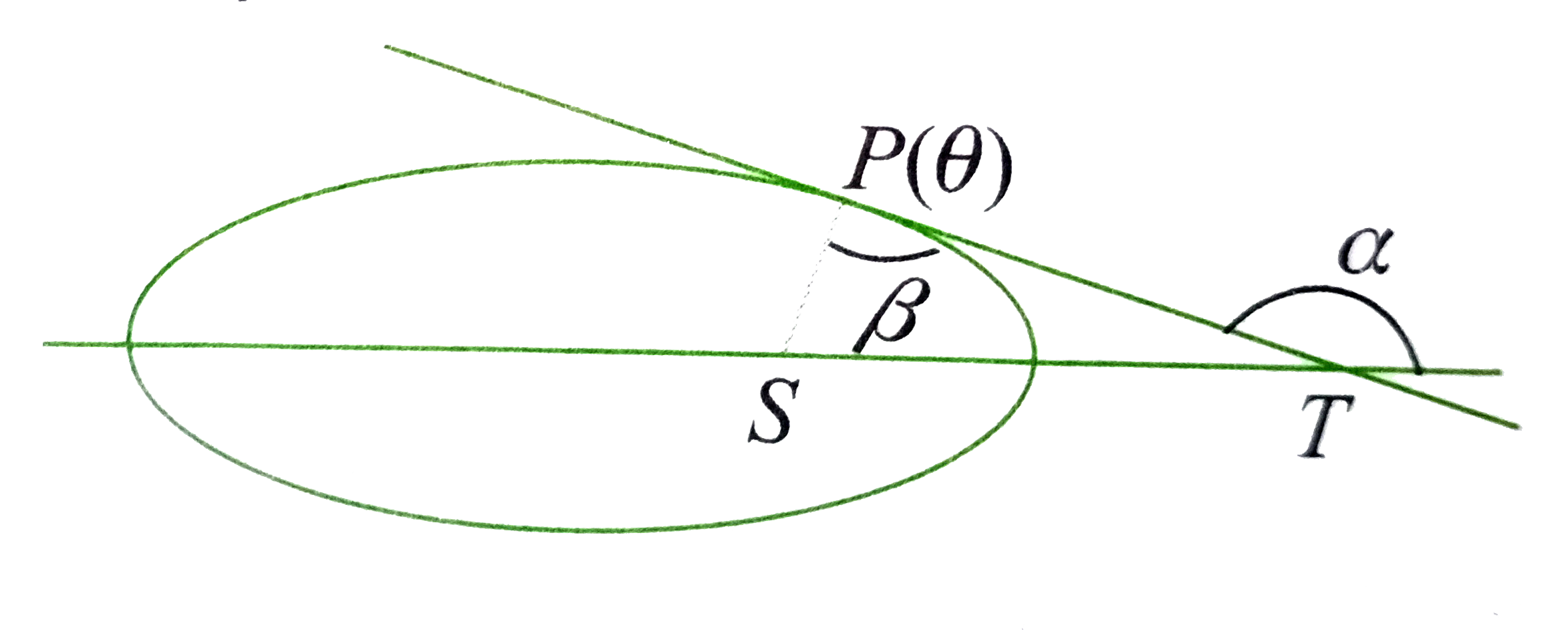
The slop of tangent is −bacotθ=tanα
orb2a2=tan2α(sec2θ−1)
=tan2α(sin2β−sinαcos2α)
=sin2β−sin2αcos2α
ore=√1−sin2β−sin2αcos2α
=√1−sin2βcos2α=cosβcosα
Normals
( 1 ) Point form: Equation of the tangent to the ellipse at (x1,y1) is x⋅x1a2+yy1b2. The slope of the tangent at (x1,y1)=−(x1a2)×(b2y1)
Slope of the normal at (x1,y1)=(a2x1)×(y1b2)=a2⋅y1b2⋅x1
Hence the equation of the normal at (x1,y1) is y−y1=ay1b2x1(x−x1)or x−x1x1a2=y−y1y1b2
( ii ) Parametric form: In above equation if we put x=acos(θ) and y=bsin(θ) then we will get normal equation in parametric form
axsec(θ)−bycosec(θ)=a2−b2=a2e2
This is equation of normal in parametric form.
( iii ) Equation of a normal in terms of its slope m is y=mx−(a2−b2)m√a2+b2m2
Example 9
Find the equation of the normal to the ellipse x2a2+y2b2=1 at the positive end of the latus rectum.
The equation of the normal at (x1,y2), to the given ellipse is
a2xx1−b2yy1=a2−b2
Here, x1 =ad and y1=b2/a
So, the equatio of the normal at the positive end of the latus rectum is
a2xae−b2yb2/a=a2e2 [∴b2=a2(1−e2)]
or axe−ay=2e2orx−ey−e3a=0
Example 10
If the straight line 4ax+3by=24 is a normal to the ellipse x2a2+y2b2=1(a>b), then find the the coordinates of focii and the ellipse
Given normal is 4ax+3by=34 (1)
Let this line be normal to the ellipse at P(acosθ,bsinθ) is axsecθ−by cosecθ=a2−b2 (2)
Equations (1) and (2) are identical, so secθ4=−cosecθ3=a2−b224
∴cosθ=6a2−b2andsinθ=−8a2−b2
Squaring and adding, we get
64(a2−b2)2+36(a2−b2)2=1
⇒100=(a2−b2)2
⇒a2−b2=10 (∴a>b)
⇒a2e2=10
Hence, foci are (±√10,0)
Example 11
If the normal at one end of the latus rectum of the ellipse x2a2+y2b2=1 passes through one end of the monor axis, then prove that eccentricity is constant.
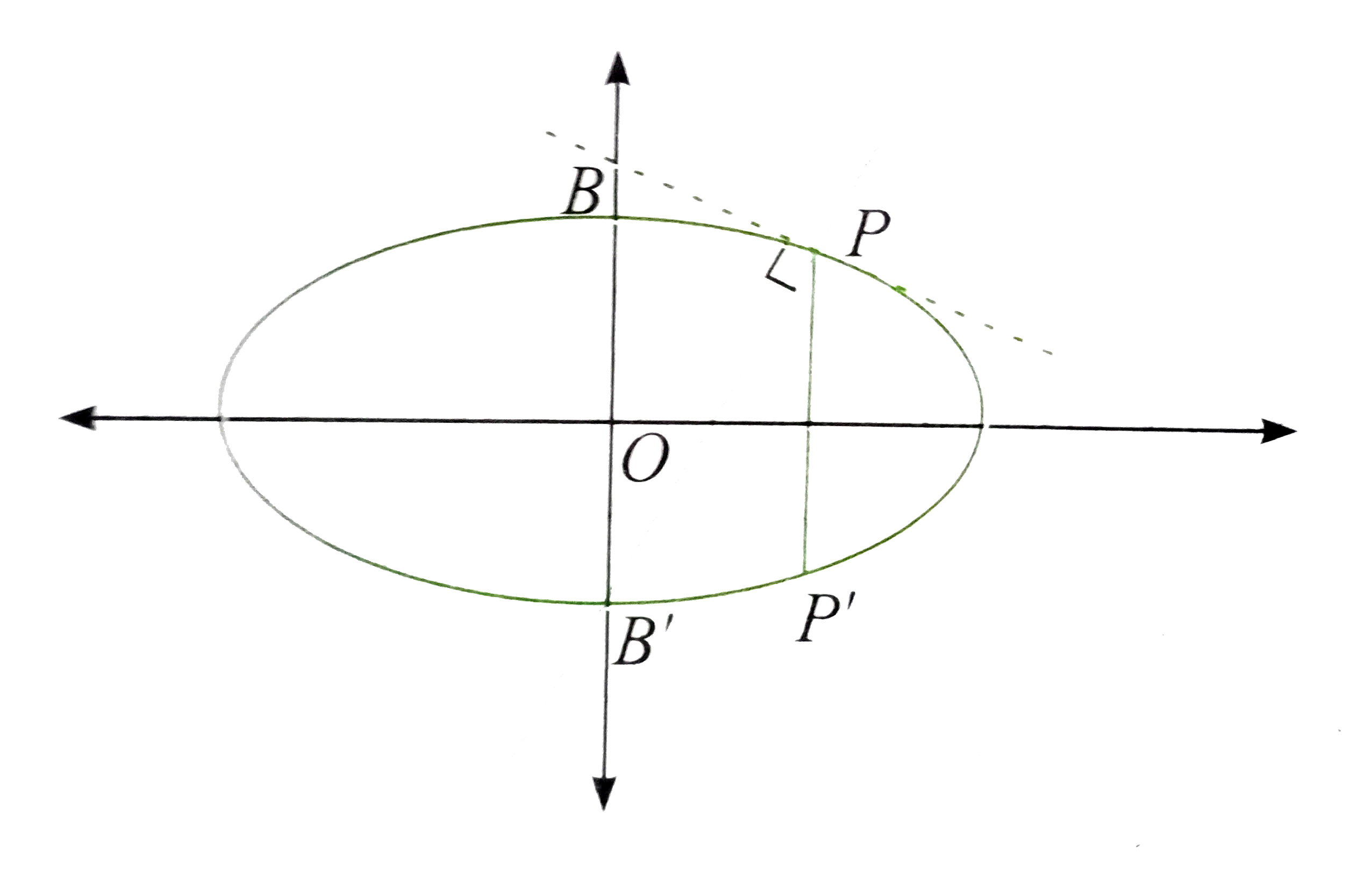
The equation of the normal at the extermity P of latus reactum is x−ey=ae3
This passes through the extermity of the minor i.e.,B'(0,-b).
Then, 0+eb−ae3=0
orba2 orb2=a2e4
or a2(1−e2)=a2e4 ore4+e2−1=0
Example 12
The number of distinct normal lines that can be drawn to the ellipse x2169+y225=1 from the point P(0,6) is
x2169+y225=1
The equation of normal at the point (13cosθ,5sinθ) is 13xcosθ−5ysinθ=144
It passes through (0,6). Thereofore, 0−30=144sinθ
orsinθ=−524
or θ=2π−sin−1.(524)andπ+sin−1.524
Also, the y-axis is one of the normals.