Level 2 from ARIHANT PHYSICS Chapter 6 GEOMETRICAL OPTICS for Class 12
| Class 12 | PHYSICS |
| Chapter | GEOMETRICAL OPTICS |
| ARIHANT PHYSICS | Level 2 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
A car is travelling at night along a highway shaped like a parabola with its vertex at the origin of the co-ordinate system. The car starts at a point 200 m West and 200 m North of the origin and travels in easterly direction. There is an animal standing 200 m East and 100 m North of the origin. At what point on the highway will the car’s headlight illuminate the animal?
 View Solution
View SolutionQuestion 3
Consider the situation shown in the Figure. The mirror AB forms image of point object P. Co-ordinates of A, B and P are (0, 10) m, (0, 8) m and (–2,0)m respectively. Two observers O1 and O2 are located at (–2,10)m and (–1,13)m respectively.
(a) One of the two observers cannot see the image of point P. Identify the observer.
(b) To ensure that both the observers are able to see the image, it was decided to use a longer mirror. Keeping the upper end of the mirror fixed at A (0, 10) m, what is the minimum length of mirror required so that both observers can see the image of point P?
 View Solution
View SolutionQuestion 4
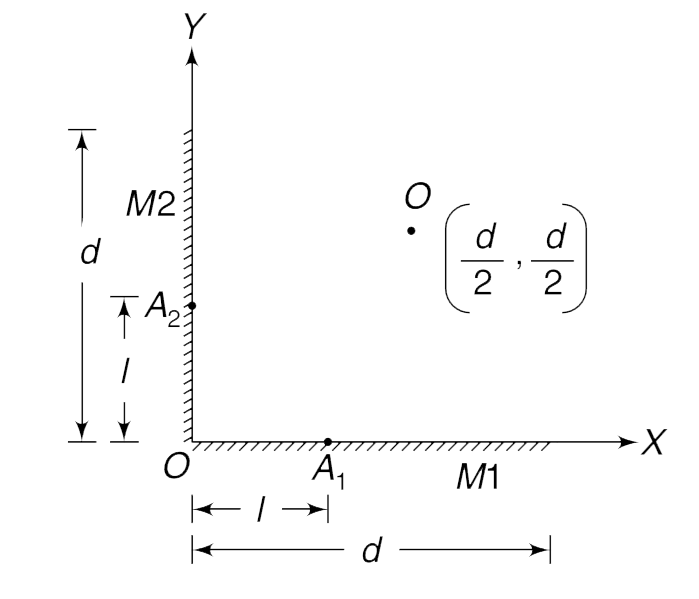
Two plane mirrors M1 and M2 of length d each are placed at right angle as shown. A point object O is placed symmetrically with respect to the mirrors at co-ordinates (d2,d2)
(a) How many images of O will be seen?
(b) Show that all the images lie on a circle.
(c) Length l(=OA1=OA2) of both the mirrors is cut and removed. Find least value of l such that only two images of the object are formed.
 View Solution
View SolutionQuestion 6
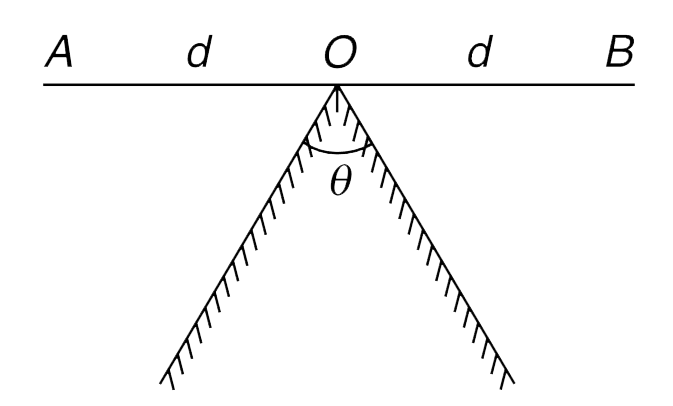
Two plane mirrors are joined together as shown. Two point objects A and B are placed symmetrically such that OA=OB=d.[AOB is a straight line]
(a) If the images of A and B coincide find θ (call it θ0).
(b) Keeping the position of objects unchanged the angle between the two mirrors is increased to θ=43θ0. Now find the distance between the images of A and B.
 View Solution
View SolutionQuestion 8
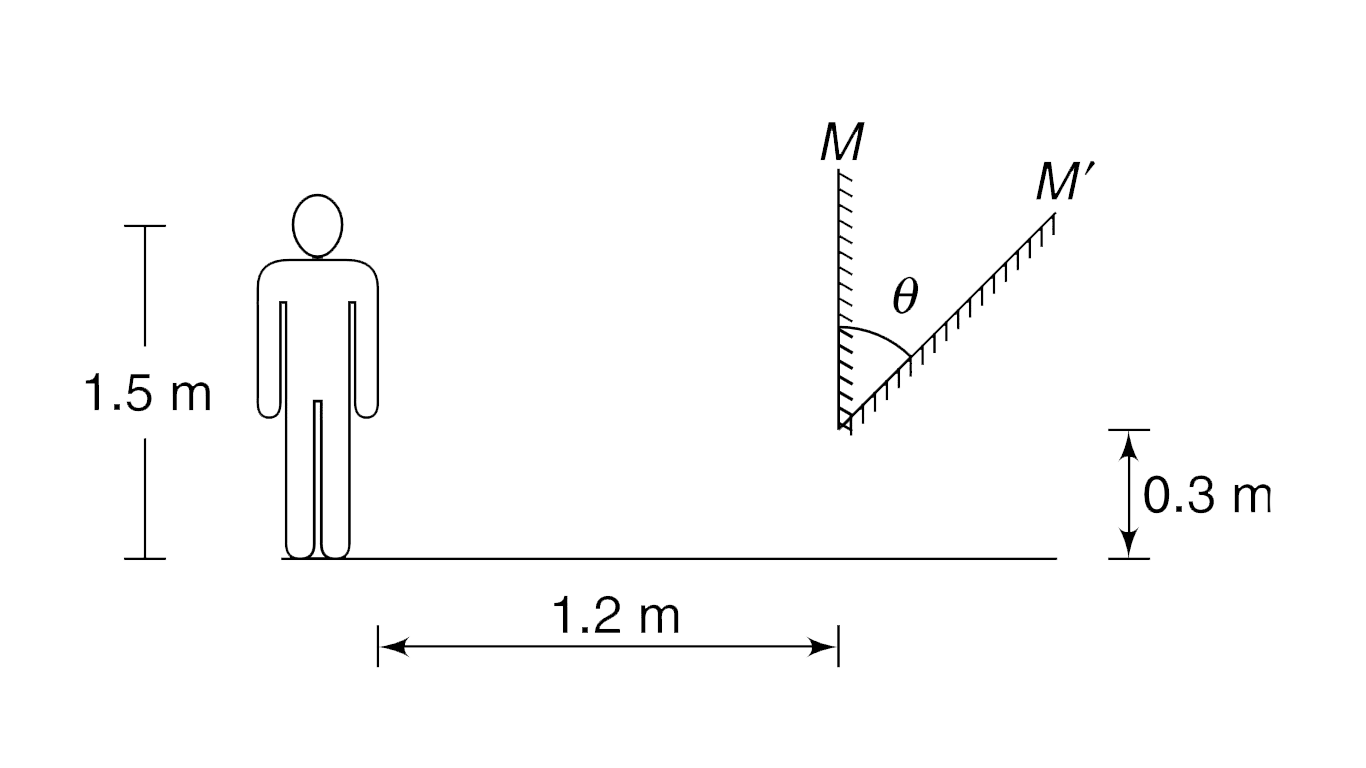
The distance between the eye and the feet of a boy is 1.5 m. He is standing on a flat ground and a vertical plane mirror M is placed at a distance of 1.2 m from the boy, with its lower edge at a height of 0.3 m from the ground. Now the mirror is tilted about is lower edge as shown in the Figure. Find maximum value of angle θ for which the image of feet remains visible to the boy. [Take sin15∘=14]
 View Solution
View SolutionQuestion 9
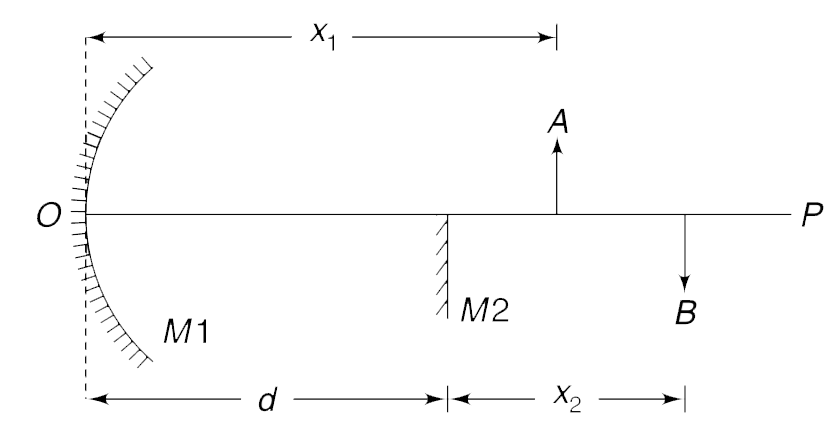
OP is the principal axis of a concave mirror M1. Just below the axis a plane mirror M2 is placed at a distance d from the concave mirror. Two small pins A and B are placed on the principal axis as shown. By moving M2 and changing d, the virtual image of A formed in mirror M1 and the virtual image of B formed in mirror M2 were made to coincide.
(a) Calculate the focal length of the concave mirror if it was found that the images coincide when separation between the mirrors was d0.
(b) Can the two virtual images be observed by the eye simultaneously?
 View Solution
View SolutionQuestion 11
Two spherical concave mirrors of equal focal length are put against each other with their reflecting surfaces facing each other. The upper mirror has an opening at its centre. A small object (O) is kept at the bottom of the cavity so formed (see Figure). The top mirror produces a virtual image of the object and the lower mirror then creates a real image of the virtual image. The second image is created just outside the cavity mouth. This creates an optical illusion as if the object is raised above its original position.
(a) Prove that the height h shown in the Figure is related to focal length of the mirror as
1f=1h+1h+(1h−1f)−1
(b) Rewrite the above equation in terms of x=hf and solve if for x.
 View Solution
View SolutionQuestion 12
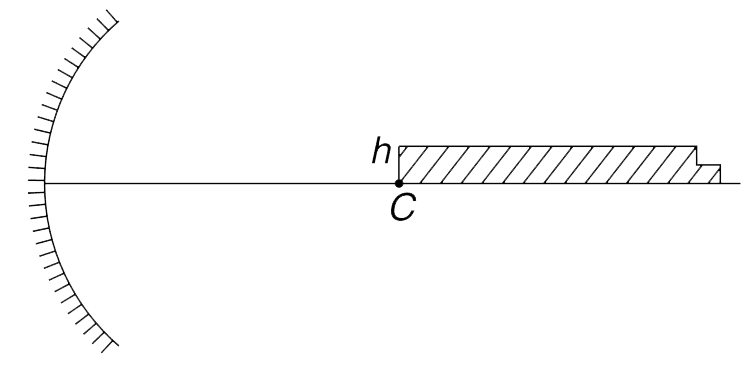
A long rectangular strip is placed on the principal axis of a concave mirror with its one end coinciding with the centre of curvature of the mirror (see Figure). The width (h) of the object is very small compared to the focal length ( f ) of the mirror. Calculate the area of the image formed.
 View Solution
View SolutionQuestion 13
A pencil (AB) of length 20 cm is moving along the principal axis of a concave mirror MM', with a velocity 5m/s approaching the mirror. The mirror itself is moving away from the pencil at a speed of 2 m/s. Find the rate of change of length of the image of the pencil at the instant end A is at a distance of 60 cm from the mirror.
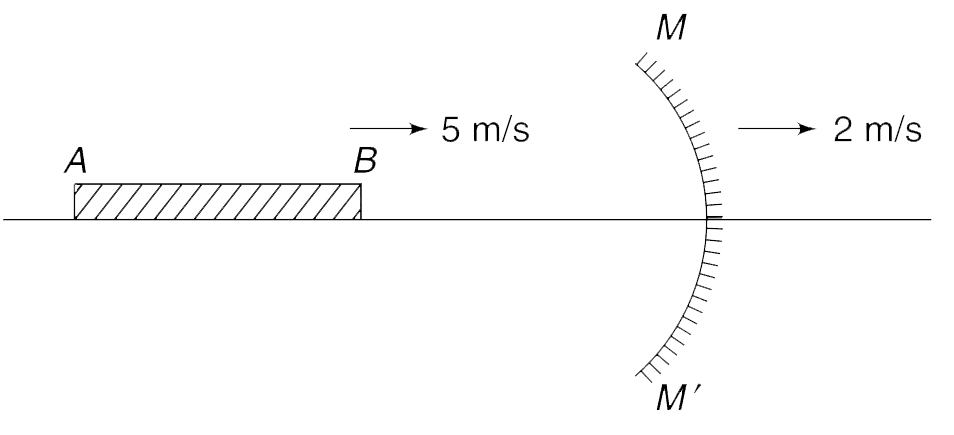 View Solution
View SolutionQuestion 14
A small object of height h is placed perpendicular to the principal axis of a convex mirror of focal length f at a distance x from the pole of the mirror. An observer is located on the principal axis at a distance L from the pole of the mirror. (Take x,f,L>>h].
(a) Calculate the angle α formed by the image at the eye of the observer
(b) If the convex mirror is replaced by a plane mirror, with all other things remaining unchanged, calculate the angle β formed by the image at the eye.
(c) Justify the statement “objects are closer than they appear” written on the rear view mirror of your car. View SolutionQuestion 15
Consider a large parabolic mirror whose section can be represented by y=kx2, where k is a positive number. Show that a parallel beam of light travelling in negative y direction, after reflection from the mirror, gets focused at a point (0,14k) . If you need a parallel beam of light, will you prefer a parabolic reflector over a spherical one?
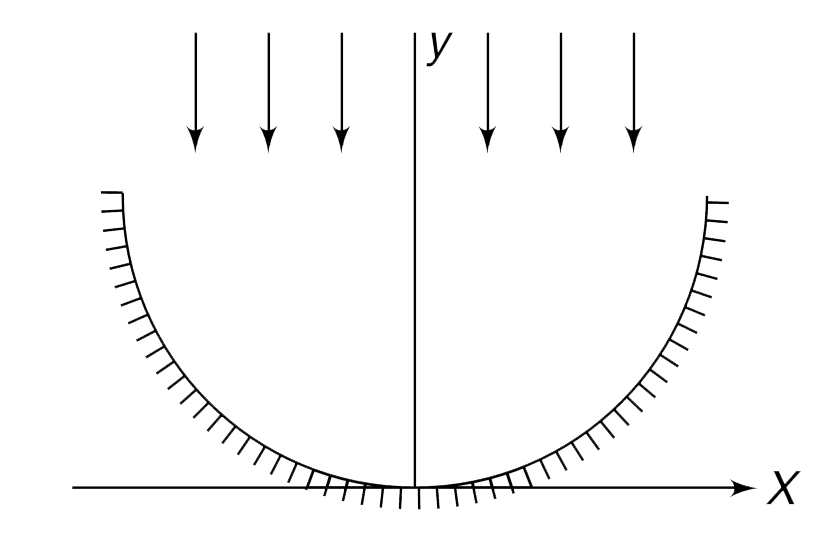 View Solution
View SolutionQuestion 16
Figure shows a glass (μg=1.5) vessel, partly filled with water (μw=43) . A ray of light is incident normally on the water surface and passes straight through. The vessel is tilted slowly till angle θ such that the light ray is emergent grazing the lower surface of the glass. Find θ.
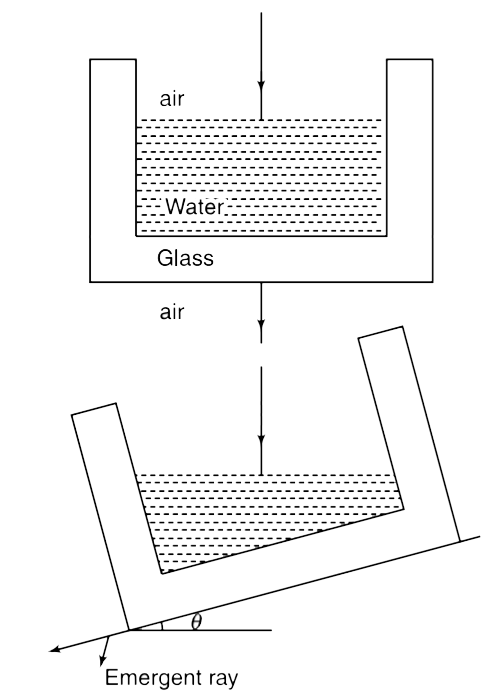 View Solution
View SolutionQuestion 17
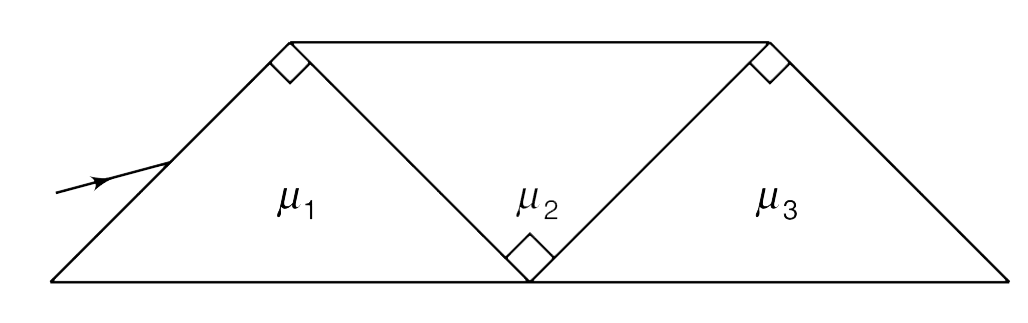
Two plane mirrors M1 and M2, placed at right angles, form two sides of a container. Mirror M1 is inclined at an angle θ0 to the horizontal. A light ray AB is incident normally onM1. Now the container is filled with a liquid of refractive index μ so that the ray is first refracted, then reflected at M1. The ray is next reflected at M2 and then comes out of the liquid surface making an angle θ with the normal to the liquid surface. Find θ.
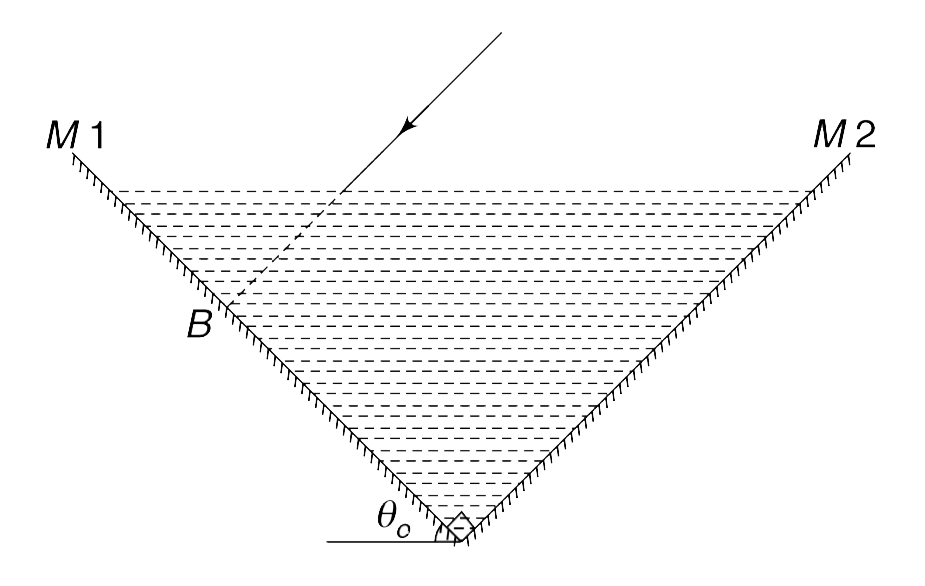 View Solution
View SolutionQuestion 18
When the sun appears to be just on horizon, it is in fact below the horizon. This is because the light from the sun bends when it enters the earth’s atmosphere. Let us assume that atmosphere is uniform and has index of refraction equal to μ. It extends upto a height h(<<R= radius of earth) above the earth’s surface. In absence of atmosphere how late would we see the sunrise compared to what we see now? Take time period of rotation of earth to be T. Calculate this time for following data
R=6400km,μ=1.0003,h=20km,T=24hr. View SolutionQuestion 19
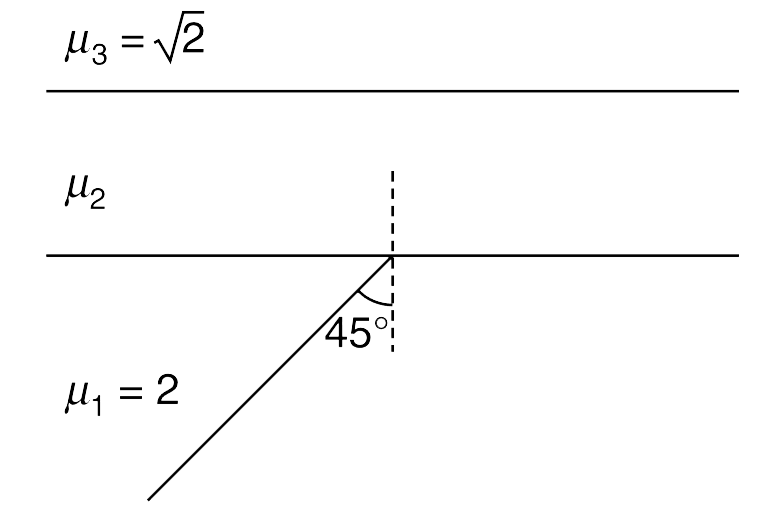
Intensity of a light beam can be defined as amount of light energy incident in unit time on a unit area held normal to the direction of beam. A light beam of intensity I0 has a circular cross section of diameter d0. This beam is travelling in a medium of refractive index μ=√2and gets incident on the medium – air boundary at an angle of incidence i=30°. Assume that entire light energy gets transmitted into air. Find the intensity (I) of transmitted light beam.
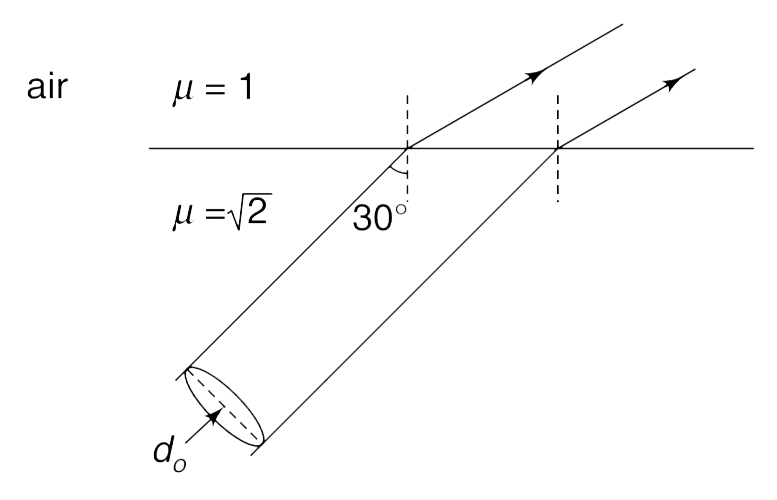 View Solution
View SolutionQuestion 21
A fibre optic cable has a transparent core of refractive index 1.6 and the cladding has a refractive index of 1.5. An optical signal travels along path A and another signal travels along path B such that it strikes the core – cladding interface at an angle of incidence θ that is just greater than the critical angle. Length of the cable is 1500 m.
(a) Find the time difference between the two signals reaching the other end of the cable.
(b) A digital signal shown in the Figure. is transmitted through the cable. Find maximum frequency so that the crest from path A never arrives with a trough from path B at the receiving end of the cable.
 View Solution
View SolutionQuestion 22
An optical fibre has diameter d and is made of material of refractive indeed μ. It is surrounded by air. Light is made to enter through one end of the fibre as shown. The fiber is in the shape of a circular bend of outer radius r.
(a) Find least value of r(=ro) for which no light can escape out of the fibre. Calculate ro for d=200μm and μ=1.4.
(b) How is value of ro affected as d is made smaller?
(c) For sharper bends, shall we have higher μ or smaller μ ?
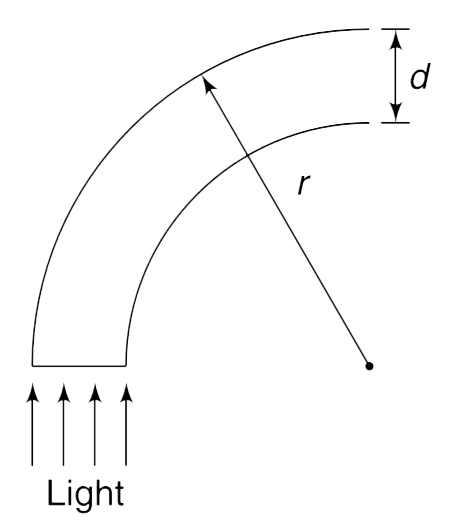 View Solution
View SolutionQuestion 23
A glass cube has side length a and its refractive index is μ=32 . A ray of light (AB) is incident normally on one of its face and after passing through the cube it forms a spot S on screen σ. The cube begins to rotate with angular speed ω about its central axis as shown in the Figure. Immediately after the cube begins to rotate, find the speed of the spot S on the screen.
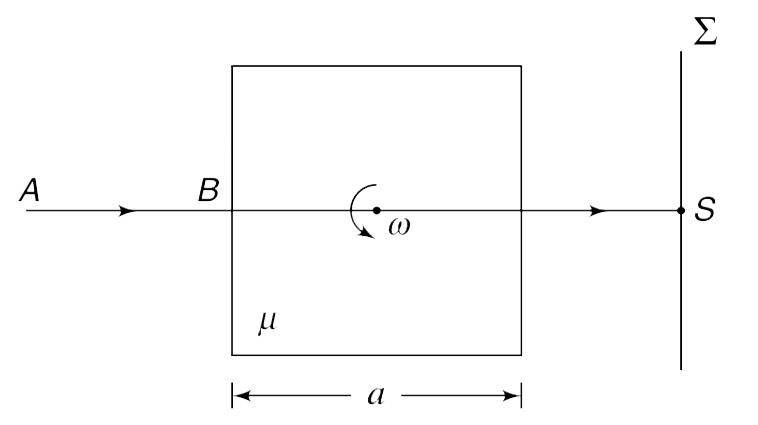 View Solution
View SolutionQuestion 24
A single ray traverses a glass plate (thickness = t) with plane surfaces that are parallel to each other. The emergent ray is parallel to the incident ray but suffers a lateral displacement d. Assuming that glass plate (refractive index μ) is placed in air, find the dependence of d on angle of incidence i. Plot the variation of d with i (changing from 0° to 90°) View SolutionQuestion 25
A transparent semicylinder has refractive index μ=√2 . A parallel beam of light is incident on its plane surface making an angle of 45° with the surface. The incident beam extends from O to A on the plane surface. Find the maximum width OA (in terms of radius R of the cylinder) so that no ray suffers total internal reflection at the curved surface. [O is the centre of the circular cross section of the cylinder]
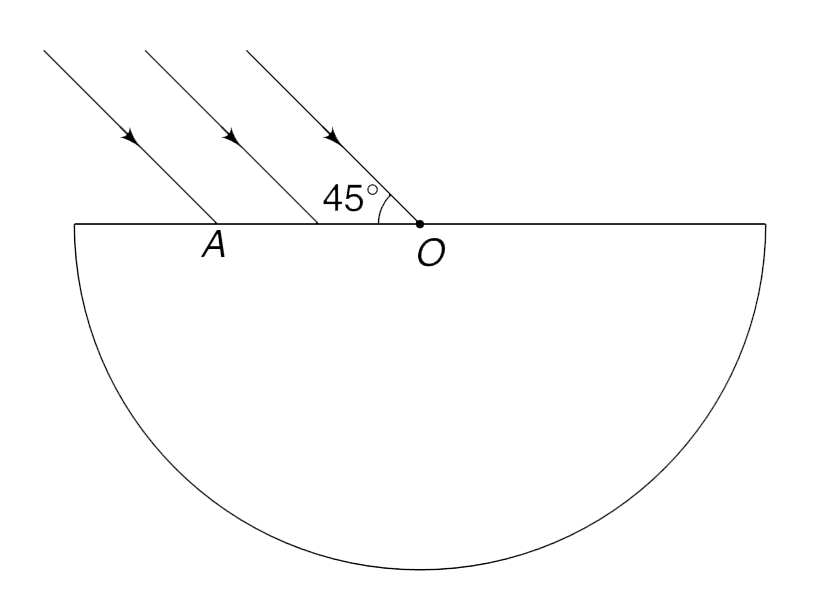 View Solution
View SolutionQuestion 26
A diver D is still under water (μ=43) at a depth d=10m. A bird is diving along line AB at a constant velocity in air. When the bird is exactly above the diver he sees it at a height of 50 m from himself and velocity of the bird appears to be inclined at 45° to the horizontal. At what distance from the diver the bird actually hits the water surface.
 View Solution
View SolutionQuestion 28
ABC is a glass prism with ∠A=90° and other two angles 45° each

(a) Prove that any light ray that enters the prism through face AB will emerge out through the face AC if refractive index of the glass of the prism is μ≥√2 .
(b) A ray of light is incident parallel to BC at a height h = 3.0 cm from BC. Find the height above BC at which the emergent ray leaves the surface AC. It is given that μ=√2 and length BC=20cm. [Take tan15°0.25]View SolutionQuestion 29
An isosceles glass prime ( refractive index =32) has its base just submerged in water ( refractive index =43) . The base of the prism is horizontal. A horizontal light ray AB is incident on the prism and takes a path shown in figure to emerge out of the prism. Find the maximum value of base angle θ of the prism for which total internal reflection can take place at the base.
 View Solution
View SolutionQuestion 31
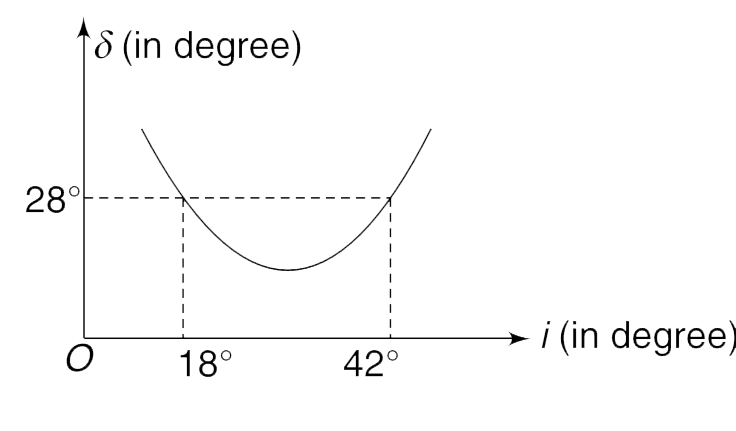
A prism has refracting angle of 60° and its material has refractive index 1.5 and 1.6 for red and violet light respectively. A parallel beam of white light is incident on one face of the prism such that the red light undergoes minimum deviation. Find the angle of incidence (i) and the angular width (θ) of the spectrum obtained.
Given: sin(49∘)=0.75∘,sin(28∘)=0.47,sin(32∘)=0.53,sin(58∘)=0.85View SolutionQuestion 32
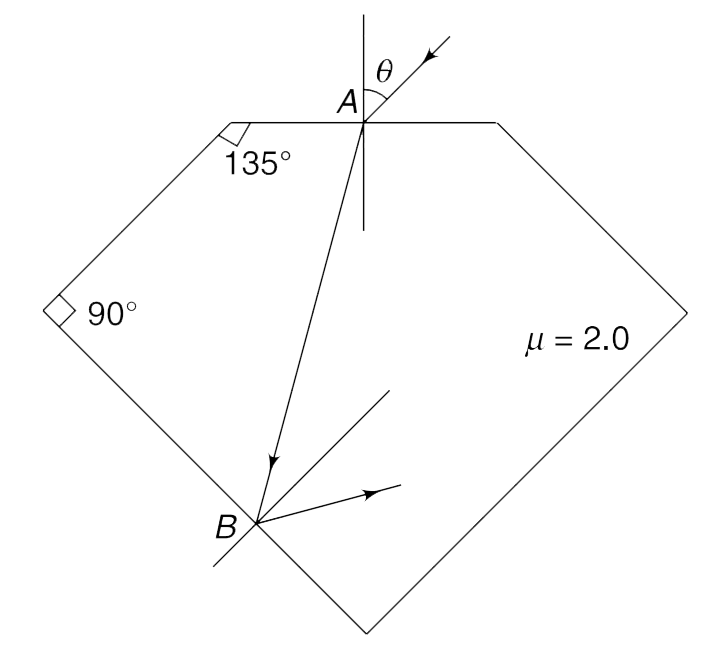
A converging beam of light is incident on a right angled isosceles prism as shown in the Figure. The marginal rays in the beam are incident at angle ±θ. The refractive index for the glass of the prism is μ=1.49(=1sin42°) . Find the maximum value of θ for which no light comes out of the hypotenuse surface.
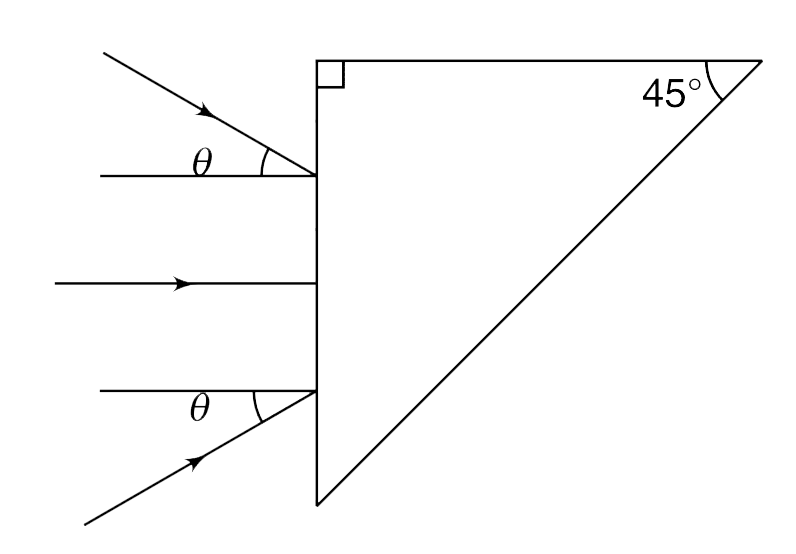 View Solution
View SolutionQuestion 33
An equilateral prism is made of glass whose refractive index for red and violet light is 1.510 and 1.550 respectively. White light is incident at an angle of incidence i and the prism is set to give minimum deviation for red light. Find
(a) angle of incidence
(b) angular dispersion (i.e., angular width of the spectrum).
Given
θ=28∘32∘50∘55∘sinθ=0.4870.5290.7550.819 View SolutionQuestion 36
Two identical equilat- eral glass (refractive index =√2) prisms ABC and CDE are kept such that the angle between faces AC and CE is q. A ray of light is incident at an angle i at the face AB and traverses through the two prisms along the path PQRSTU. Find the value of angle i and θ such that angle between the incident ray PQ and emergent ray TU is minimum.
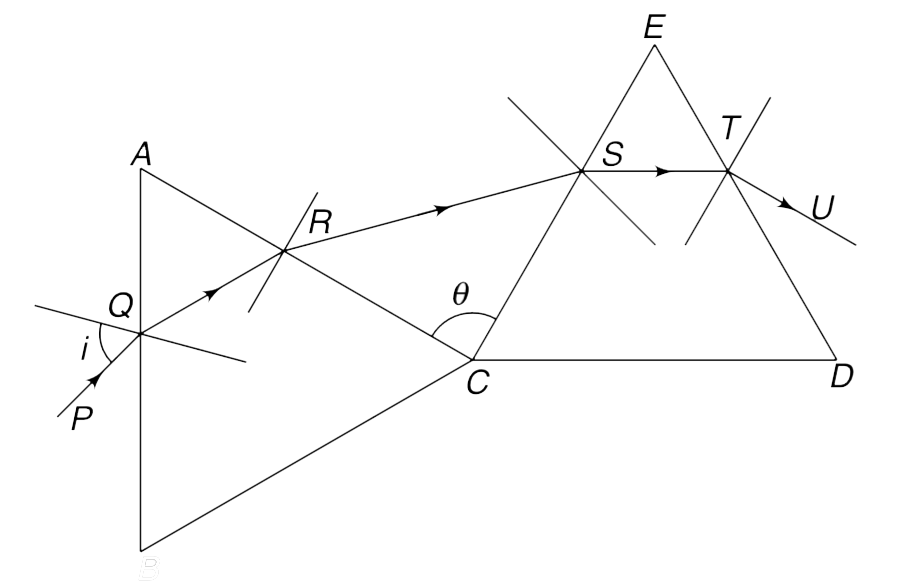 View Solution
View SolutionQuestion 37
An equilateral prism of refractive index μ=4√3 is kept in a medium of refractive index μ1. Consider a light ray to be normally incident on one of the refracting faces. The diagram shows variation of magnitude of angle of deviation (β) with respect to μ1.
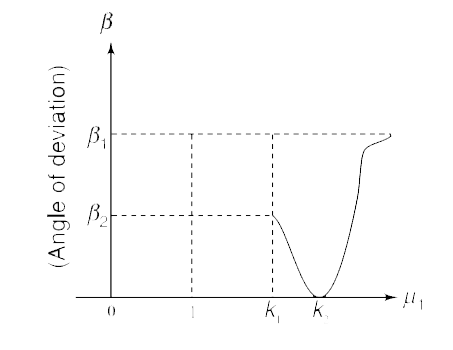
(a) Find value of k2.
(b) Find value of k1. View SolutionQuestion 38
A rectangular glass block (μ=1.5) is on top of a sheet of paper on which there on which there is a small dot. There is a layer of liquid between the paper and the glass block. The dot is visible through a vertical face up to a point where the angle of emergence of light (starting from the dot) is 30°. Find the refractive index (m0) of the liquid. Can we see the dot through a vertical face if the liquid layer is replaced with air? sin−1.23=42∘View SolutionQuestion 39
A light ray travelling in a medium of refractive index μ1 is incident on a parallel faced glass slab making an angle of θ with the glass surface. The refractive index of the medium on the other side of the glass slab is μ3(>μ1). Find the angular deviation suffered by the light ray.
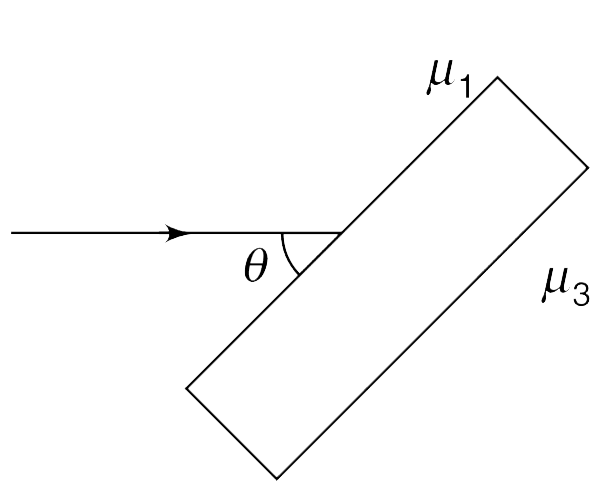 View Solution
View SolutionQuestion 40
The Figure shows the equatorial circle of a glass sphere of radius R having centre at C. The eye of an observer is located in the plane of the circle at a distance R from the surface. A small insect is crawling along the equatorial circle.
(a) Calculate the length (L) of the are on the circle where the insect lies where its image is visible to the observer.
(b) Calculate the value of L when the eye is brought very close to the sphere. Refractive index of the glass is μ=1√2
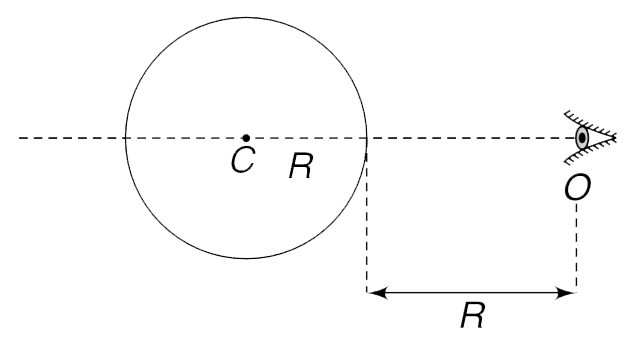 View Solution
View SolutionQuestion 41
On a hot summer day in a desert the refractive index of the atmosphere changes with height (y) above the surface of the earth as μ=m0(1+by)1/2 where m0 is the refractive index at the surface and b=6×x10−4m−1. A man of height 1.5 m is standing on a straight level road. Calculate the distance beyond which he cannot see a point on the road. View SolutionQuestion 43
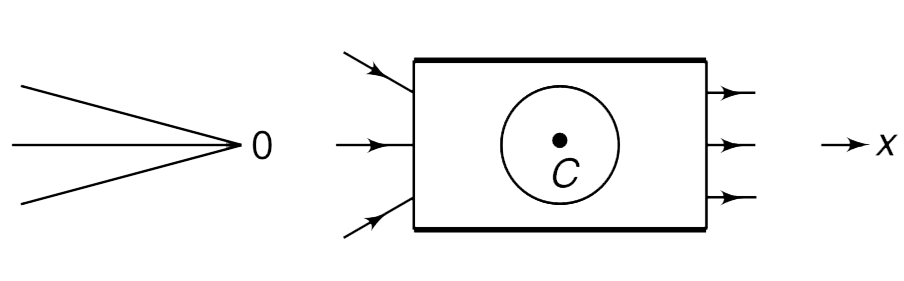
A beam of light rays converges to a point O on x-axis as shown. The angle of convergence is small. A cube of glass of refractive index μ=1.5 and side length 40cmcontaining a concentric spherical air cavity of radius 10 cm is to be placed in the path of the converging beam so that the beam emerging from the cube is parallel to x-axis. At what point C on x-axis should the centre of the cube be placed to achieve this? Give the x coordinate of C taking O as origin.
 View Solution
View SolutionQuestion 44
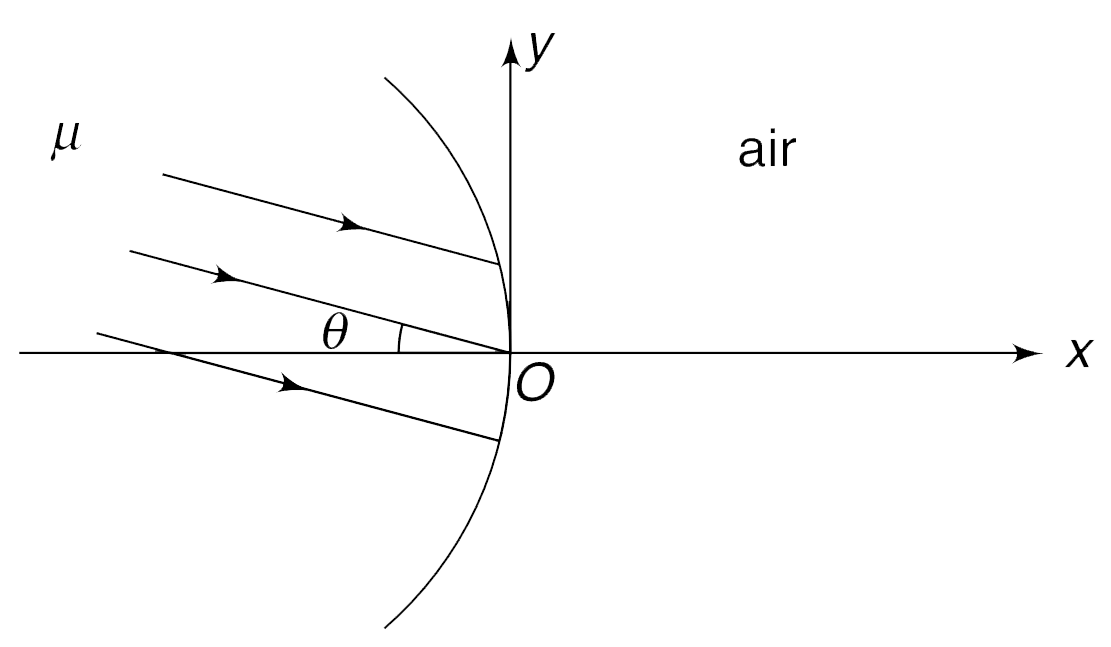
A spherical surface of radius R separates air from a medium of refractive index μ. Parallel beam of light is incident, from medium side, making a small angle θ with the principal axis of the spherical surface. Find the co-ordinates of the point where the rays will focus in air.
 View Solution
View SolutionQuestion 45
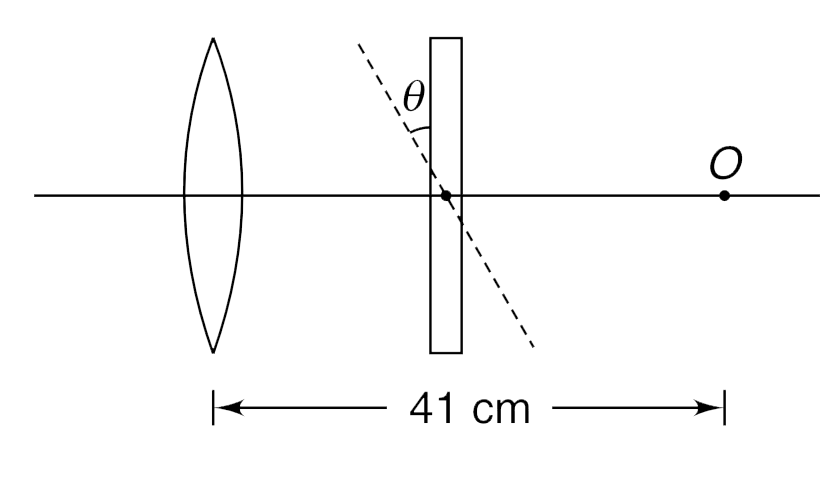
A point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
 View Solution
View SolutionQuestion 46
A man is Standing on the peak of a mountain and finds that evening sun rays are nearly horizontal. At a horizontal distance of 6 km from him, its raining and he sees a beautiful rainbow. The sun rays entering water drop get refracted, reflected and refracted to form a rainbow. The red light is emitted from a drop upto a maximum angle of 42° with respect to the incident sunlight. In front of the man there is a flat valley at a depth of 0.5 km from the mountain peak. What fraction of the complete circular arc of the rainbow is visible to the man? View SolutionQuestion 48
An observer holds in front of himself a thin equi convex lens. R is the radius of curvature of each face. He sees two images of his nose, one erect and the other inverted. Explain the formation of these images and assuming the refractive index of glass to be 1.50 prove that he will see two erect images if the distance of the lens is less than 0.25 R from his nose. View SolutionQuestion 49
An observer is standing at a point O, at a distance of 100 cm from a convex lens of focal length 50 cm. A plane mirror is placed behind the lens at a distance of 150 cm from the lens. The mirror now starts moving towards the right with a velocity of 10cm/s. What will be the magnitude of velocity (in m/s) of her own image as seen by the observer, at the moment when the mirror just starts moving?
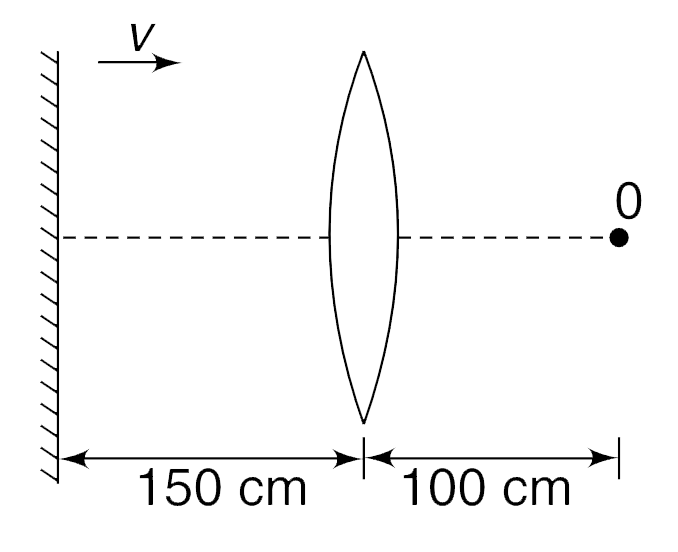 View Solution
View SolutionQuestion 50
A small object (A) is placed on the principal axis of an equiconvex lens at a distance of 30 cm. The refractive index of the glass of the lens is 1.5 and its surfaces have radius of curvature R=20cm. Two glass slabs S1 and S2 have been placed behind the lens as shown in Figure. Thickness of the two slabs is 6 cm and 4 cm respectively and their refractive indices are 32 and 2 respectively.
(a) Find the distance of the final image measured from the lens. Also find the magnification.
(b) How does the position of the image change if the slab S2 is moved to left so as to put it in contact with S1.
(c) How does the position of the image change if the two slabs in contact are together moved to right by a distance of 100 cm.
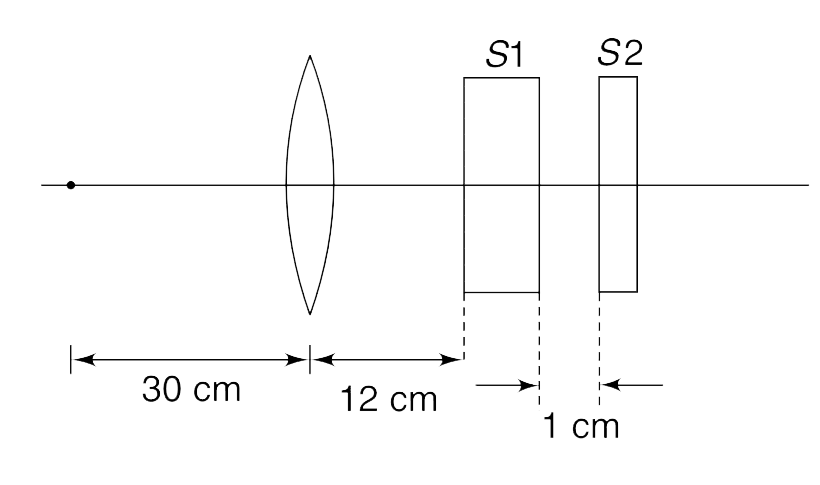 View Solution
View SolutionQuestion 52
An equiconvex lens of refractive index 1.5 has its two surfaces having radius of curvature of 30 cm. A point object has been placed on the principal axis at a distance of 60 cm from the lens. Find the distance of image from the lens formed by the rays which suffer refraction at first surface, reflection at second surface, again a reflection on the first surface and finally a refraction from the second surface. View SolutionQuestion 53
A thin plano convex lens A has material of refractive index μA=1.8 and its curved surface has radius of curvature R. A thin layer of transparent material B is laid over the curved surface of A. The refractive index of B is μB=1.2 and the curved surface of B that is not touching a has radius of curvature R2 . This surface of B is silvered. A point object is kept at a distance of 10 cm on the principal axis of the system (above the plane surface) and its image is formed at a distance of 40 cm above the plane surface. Find R.
 View Solution
View SolutionQuestion 54
The refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB. View SolutionQuestion 56
A horizontal parallel beam of light passes through a vertical convex lens of focal length f. The optical centre of the lens is P. A small plane mirror is placed at point M inclined at 60° to the axis of the lens. Distance PM=f/2. The mirror reflects the light passing through the lens and forms an image at point I. Find distance PI.
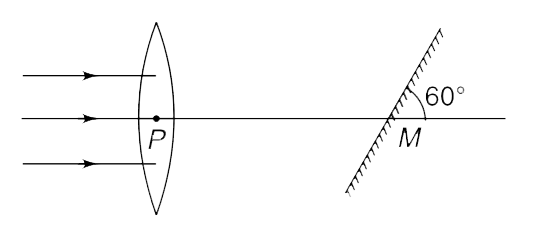 View Solution
View SolutionQuestion 57
A plane convex lens has aperture diameter of 8 mm and thickness of the lens at the centre is 3 mm. The refractive index of the material of the lens is √3 . A light ray is incident at mid point P of the curved surface at an angle of incidence of 60°.
(a) Calculate the angular deviation suffered by the ray as it passes through the lens. (b) Find the lateral shift in the path of the ray as it passes through the lens.
(c) Find the radius of curvature of the curved surface.
(d) If a narrow beam of light is incident at P parallel to the axis shown, where will it get focused. Take 2√3(√3−1)≈2.5
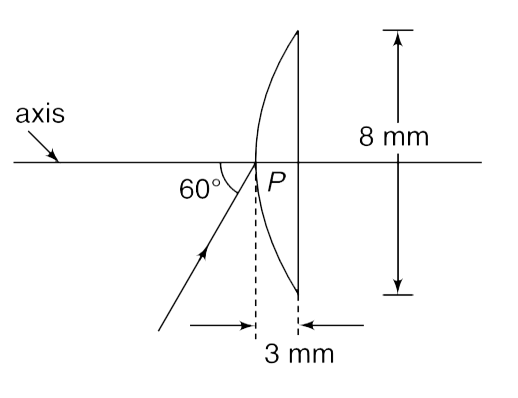 View Solution
View SolutionQuestion 58
A convex lens of focal length 20 cm and another planocovex lens of foal length 40 cm are placed co-axially. The plane surface of the plano convex lens is silvered. An object O is kept on the principal axis at a distance of 10 cm from the convex lens (see Figure). Find the distance d between the two lenses so that final image is formed on the object itself.
 View Solution
View SolutionQuestion 59
An equiconvex lens has its two surfaces of radius of curvature R=10cm. Thickness of the lens at its centre is 2 cm. A light ray is incident making an angle of 2° with the optic axis of the lens. Find the angle that the emergent ray will make with the optic axis. The refractive index of all media is as marked in the Figure.
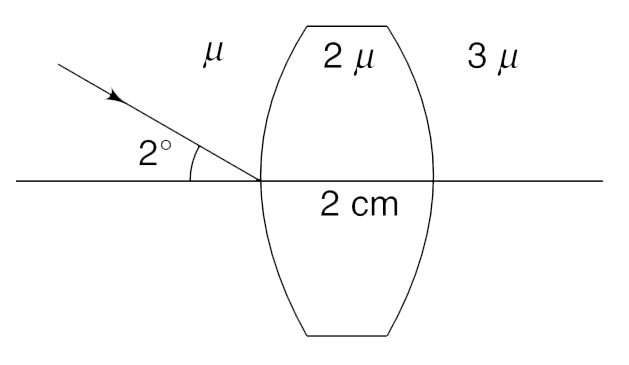 View Solution
View SolutionQuestion 60
Due to manufacturing defect, the plane surface of a thin plano-concave lens has been made tilted at a small angle q outwards from its usual place. The spherical surface has radius of curvature R and refractive index of the material of the lens is μ. A parallel beam of light is incident as shown. In the co-ordinate system shown find the co-ordinates of the point where the rays will focus or appear to be diverging from.
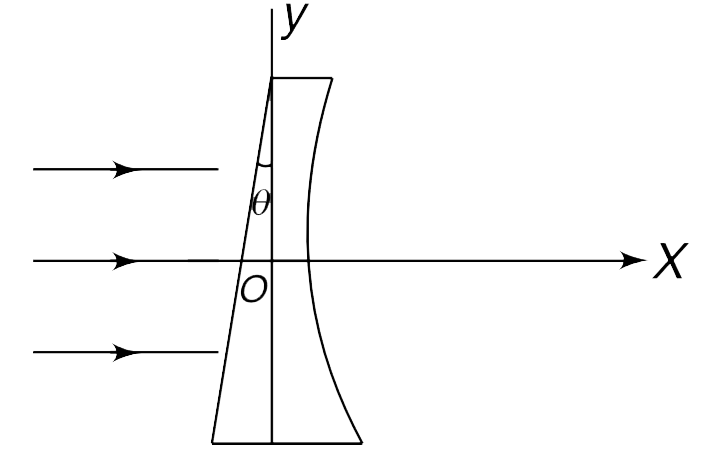 View Solution
View SolutionQuestion 61
Two lenses L1 and L2 are used to make a telescope. The larger lens L1 is a convex lens with both surfaces having radius of curvature equal to 0.5 m. The smaller lens L2 has two surfaces with radius of curvature 4 cm. Both the lenses are made of glass having refractive index 1.5. The two lenses are mounted in a tube with separation between them equal to 1 cm less than the sum of their focal length.
(a) Find the position of the image formed by such a telescope for an object at a distance of 100 m from the objective lens L1.
(b) What is the size of the image if object is 1 m high? Do you think that lateral magnification is a useful way to characterize a telescope?
(c) Angular magnification is defined as ratio of angle subtended by the image at the eyepiece to the angle subtended by the distant object at an unaided eye. Find the angular magnification of the above mentioned telescope. View SolutionQuestion 62
A convex lens of focal length 15 cm is split into two halves and the two halves are placed at a separation of 120 cm. Between the two halves of convex lens a plane mir- ror is placed horizontally and at a distance of 4 mm below the principal axis of the lens halves. An object AB of length 2 mm is placed at a distance of 20 cm from one half lens as shown in figure. Find the distance of final image of the point A from the principal axis.
 View Solution
View Solution