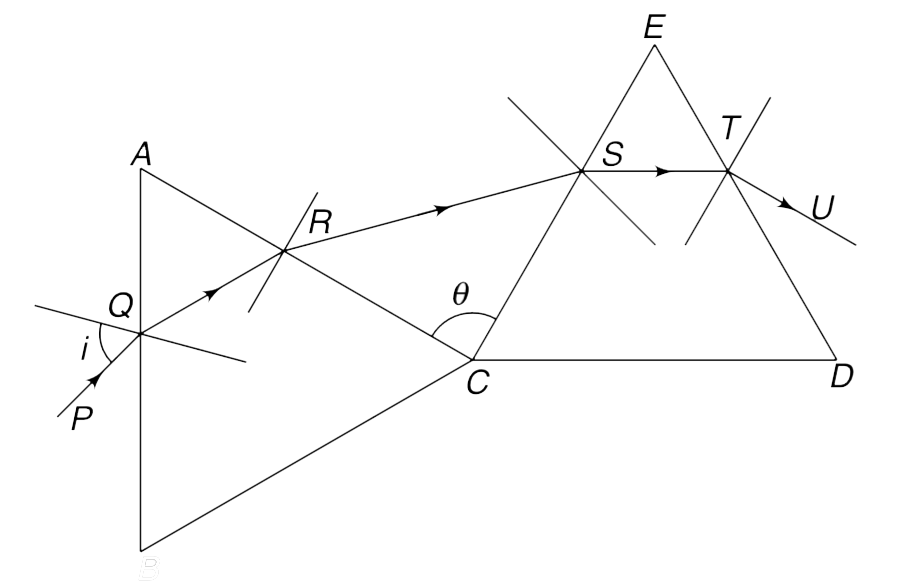
Two identical equilat- eral glass (refractive index prisms ABC and CDE are kept such that the angle between faces AC and CE is q. A ray of light is incident at an angle i at the face AB and traverses through the two prisms along the path PQRSTU. Find the value of angle i and such that angle between the incident ray PQ and emergent ray TU is minimum.
The correct Answer is:
Step by step video, text & image solution for Two identical equilat- eral glass (refractive index = sqrt(2)) prisms ABC and CDE are kept such that the angle between faces AC and CE is q. A ray of light is incident at an angle i at the face AB and traverses through the two prisms along the path PQRSTU. Find the value of angle i and theta such that angle between the incident ray PQ and emergent ray TU is minimum. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
- MAGNETIC EFFECT OF CURRENTBook:ARIHANTChapter:MAGNETIC EFFECT OF CURRENTExercise:Magnetic effect of Current
Explore 45 Videos
Similar Questions
A ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
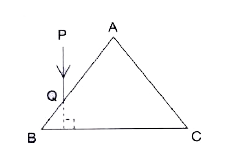
View SolutionA ray of light PQ is incident on the face AB of an equilateral glass prism ABC as shown in the figure. Show that angle of emergence = angle of deviation. Also, with a ray diagram, trace the path of the emergent ray.
View Solution
Knowledge Check
A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. The ray emerging out of the prism makes an angle of 30∘ with the incident ray. The emergent ray is
A0∘B90∘C30∘D45∘A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3An equilateral triangular prism is made of glass (μ=1.5). A ray of light is incident normally on one of the faces. The angle between the incident and emergent ray is
A60∘B90∘C120∘D180∘
A ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View SolutionA ray of light is incident on one face of a prism (m=√3) at an angle of 60∘. The refracting angle of the prism is also 60∘. Find the angle of emergence .

View SolutionA ray of light is incident normally on one of the faces of a prism of apex angle 30 degree and refractive index sqrt2. The angle of deviation of the ray is…degrees.
View SolutionA ray of light is incident normally normallyh on one of the faces of a prism of apex angle 30∘ and refractive index √2. The angle of deviation of the ray is ________________ degrees.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. The ray emerging out of the prism makes an angle of 30∘ with the incident ray. The emergent ray is
View Solution