समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 गणित
भूमिका
अध्याय के शीर्षक के अनुसार इस अध्याय मे हम समांतर चतुर्भुज और त्रिभुजों के क्षेत्रफल का अध्ययन करेंगे। पिछले दो अध्यायों में हमने त्रिभुजों और समांतर चतुर्भुजों के बारे में विस्तार से पढ़ा है, अब हम उनके क्षेत्रफल ज्ञात करने के लिए महत्वपूर्ण प्रमेय पढ़ेंगे।
ज्यामिति की शुरुआत खेतों के बीच की परिसीमाओं (Boundries) को बनाने और उन्हें उपयुक्त भागों में विभाजित करने की प्रक्रिया के क्रम में हुआ। साधारण बोलचाल की भाषा में किसी ज्यामितीय आकृति जैसे त्रिभुज, चतुर्भुज, बहुभुज, वृत्त इत्यादि के क्षेत्रफल का अर्थ उस स्थान के माप से होता है जितना स्थान वह आकृति समतल में छेंकती है।
आइये जानते है, समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल को और करीब से ...
एक सरल बंद आकृति (simple closed figure) द्वारा तल का घेरा हुआ भाग उस आकृति का संगत तलीय क्षेत्र (planar region) कहलाता है। इस तलीय क्षेत्र का परिमाण (magnitude) या माप (measure) उस आकृति का क्षेत्रफल (area) कहलाता है। इस परिमाण या माप को सदैव एक संख्या [किसी मात्रक (unit) में ] की सहायता से व्यक्त किया जाता है, जैसे 5cm2, 8m2 , 3 हेक्टेयर इत्यादि। अतः हम कह सकते कि किसी आकृति का क्षेत्रफल (किसी मात्रक में) एक संख्या है जो उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (जुड़ी) होती है।
यहाँ हम क्षेत्रफल की गूढ़ (rigorous) परिभाषा न देकर केवल उसकी सरल परिभाषा देंगे । अतः किसी आकृति का क्षेत्रफल (किसी मात्रक में) एक संख्या है जो उस आकृति द्वारा घेरे गए तल के भाग से जुड़ी होती है ।
हम दो आकृतियों के सर्वांगसमता के बारे में पढ़ चुके हैं। दो आकृतियाँ सर्वागसम होती हैं यदि उनका आकार (shape) और माप (size) समान हों । यदि दो आकृतियाँ सर्वांगसम हों तो एक को दूसरे पर रखने पर वह दूसरे को पूरा पूरा ढंँक लेती है। स्पष्टतः यदि दो आकृतियाँ सर्वांगसम हो तो उनके क्षेत्रफल समान होते हैं, लेकिन यदि दो आकृतियों का क्षेत्रफल बराबर हो तो यह आवश्यक नहीं कि दोनों सर्वांगसम हों।
उदाहरण-
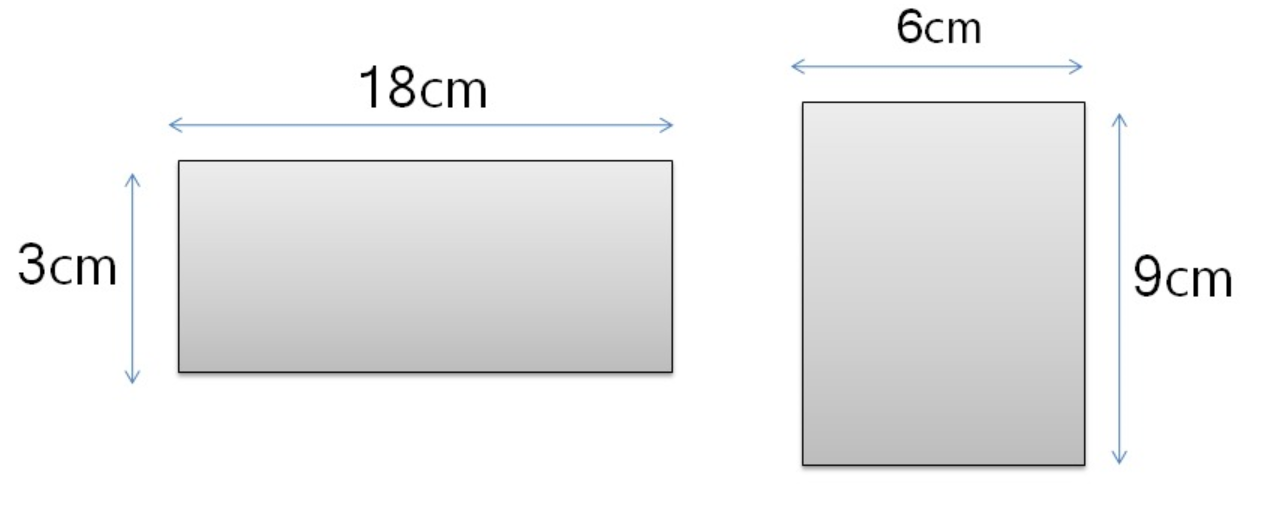
चित्र में दिए गए आयतों के क्षेत्रफल बराबर हैं।
चित्र (i) तथा (ii) में दिए गए आयतों में से प्रत्येक का क्षेत्रफल 54 cm2है लेकिन ये सर्वांगसम नहीं है ।
नीचे दिए गए चित्र के आकृति को देखने पर हम पाते हैं कि समतलीय क्षेत्र S दो समतलीय क्षेत्रों A और B को मिलाने से बना है।
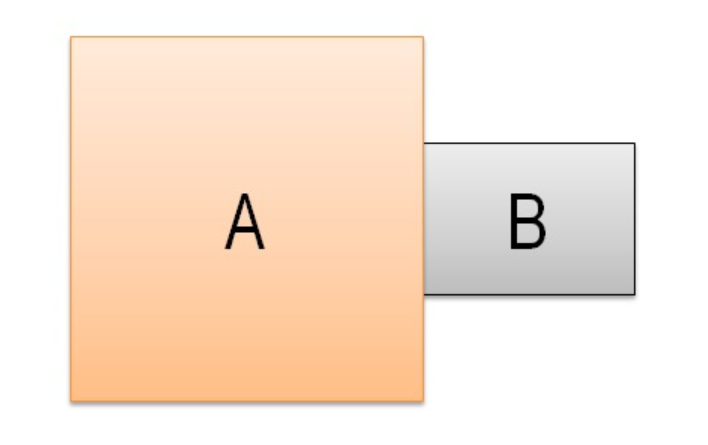
स्पष्टतः आकृति S का क्षेत्रफल = आकृति A का क्षेत्रफल + आकृति B का क्षेत्रफल
आकृति A के क्षेत्रफल को ar(A) , आकृति B के क्षेत्रफल को ar(B) , आकृति S के क्षेत्रफल को ar(S) , इत्यादि से सूचित किया जा सकता है ।
अब यह कहा जा सकता है कि किसी आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (किसी मात्रक में) एक संख्या है: जिसमें नीचे दिए गए दो गुण हैं :
1. यदि A और B दो सर्वांगसम आकृतियाँ , तो ar(A)=ar(B) है तथा
2. यदि एक आकृति S द्वारा बना क्षेत्र दो, अनातिव्यापी (non-overlapping) तलीय क्षेत्रों आकृतियों P और Q से मिलकर बना है, तो ar(S) = ar(P) + ar(Q) होगा ।
पिछली कक्षा में हम विभिन्न आकृतियों जैसे त्रिभुज, आयत, वर्ग, समान्तर चतुर्भुज इत्यादि के क्षेत्रफल निकालने की विधि के बारे में पढ़ चुके हैं। यहाँ हम इन ज्यामितीय आकृतियों के क्षेत्रफल के बीच क्या सम्बन्ध है, इसके बारे में पढ़ेंगे, यदि वे एक ही आधार पर खड़े हों और एक ही समान्तर रेखाओं के बीच स्थित हों।
एक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ
नीचे दी गई आकृतियों को देखिए:
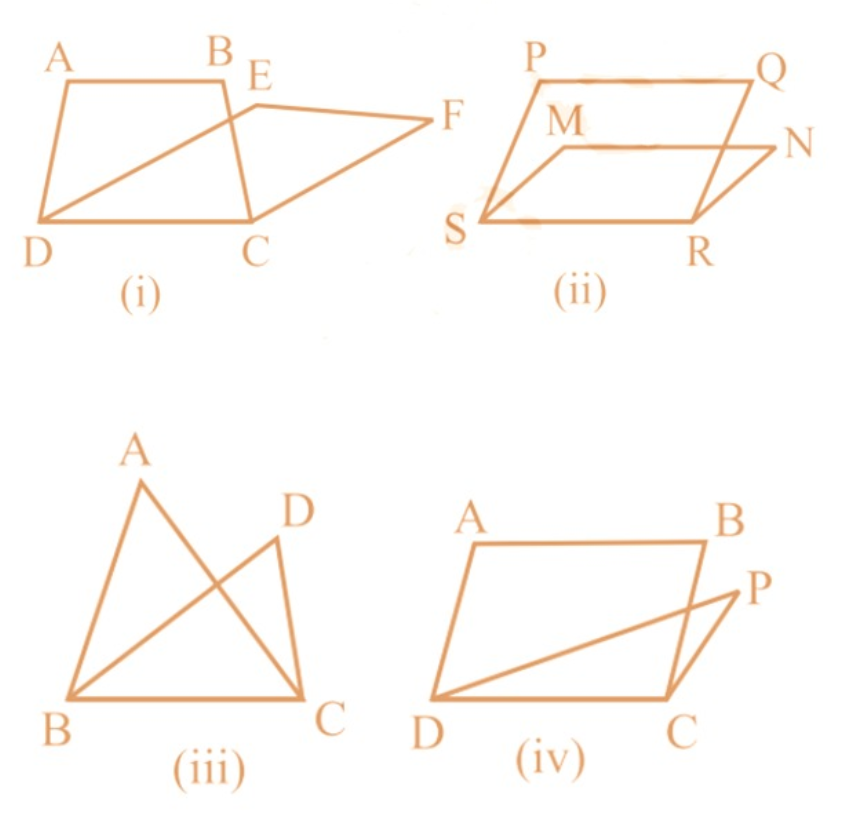
आकृति (i) में, समलंब ABCD और समांतर चतुर्भुज EFCD में एक भुजा DC उभयनिष्ठ है। हम कहते हैं कि समलंब ABCD और समांतर चतुर्भुज EFCD एक ही आधार (same base) DC पर स्थित हैं।
इसी प्रकार, आकृति (ii) में, समांतर चतुर्भुज PQRS और MNRS एक ही आधार SR पर स्थित हैं।
आकृति (iii) में त्रिभुज ABC और DBC एक ही आधार BC पर स्थित हैं।
आकृति (iv) में, समांतर चतुर्भुज ABCD और त्रिभुज PDC एक ही आधार DC पर स्थित हैं।
अब नीचे दी गई आकृतियों को देखिए-
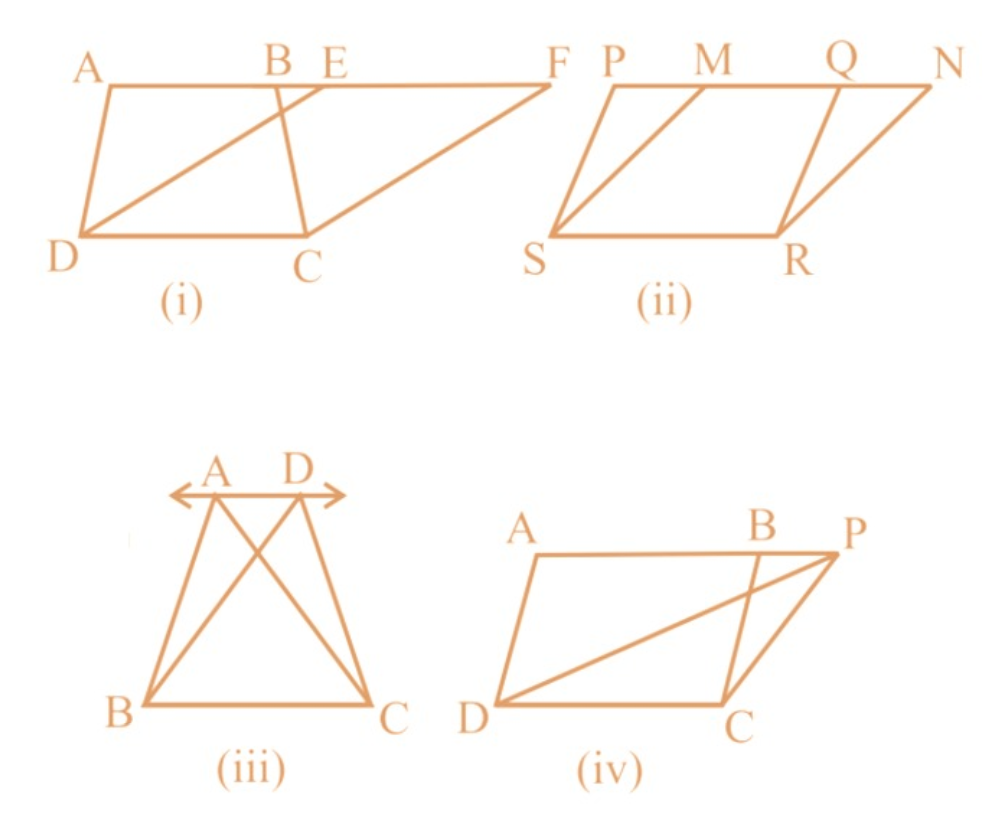
आकृति (i) में, स्पष्टत: समलंब ABCD और समांतर चतुर्भुज EFCD एक ही आधार DC पर स्थित हैं। उपरोक्त के अतिरिक्त, (समलंब ABCD के) आधार DC के सम्मुख शीर्ष A और B तथा (समांतर चतुर्भुज EFCD के) आधार DC के सम्मुख शीर्ष E और F, DC के समांतर एक रेखा AF पर स्थित हैं। हम कहते हैं कि समलंब ABCD और समांतर चतुर्भुज EFCD एक ही आधार DC तथा एक ही समांतर रेखाओं AF और DC के बीच स्थित हैं।
इसी प्रकार, समांतर चतुर्भुज PQRS और MNRS एक ही आधार SR तथा एक ही समांतर रेखाओं PN और SR के बीच स्थित हैं [देखिए आकृति (ii)] , जिसमें PQRS के शीर्ष P और Q तथा MNRS के शीर्ष M और N आधार SR के समांतर रेखा PN पर स्थित हैं।
इसी प्रकार, त्रिभुज ABC और DBC एक ही आधार BC और एक ही समांतर रेखाओं AD और BC के बीच स्थित है।
देखिए आकृति (iii)] तथा समांतर चतुर्भुज ABCD और त्रिभुज PCD एक ही आधार DC और एक ही समांतर रेखाओं AP और DC के बीच स्थित है।[देखिए आकृति (iv)]।
इसीलिए, दो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती है, यदि उनका एक उभयनिष्ठ आधार (भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (या का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
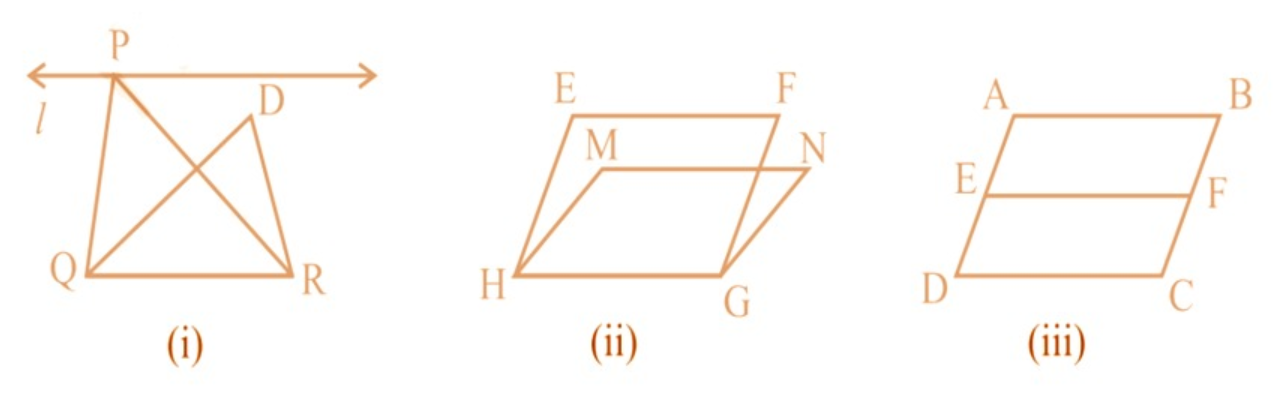
उपरोक्त कथन को दृष्टिगत रखते हुए, आप यह नहीं कह सकते कि आकृति (i) के ΔPQR और ΔDQR एक ही समांतर रेखाओं l और QR के बीच स्थित हैं। इसी प्रकार, आप यह नहीं कह सकते कि आकृति (ii)के समांतर चतुर्भुज EFGH और MNGH एक ही समांतर रेखाओं EF और HG के बीच स्थित हैं तथा यह कि आकृति (iii) के समांतर चतुर्भुज ABCD और EFCD एक ही समांतर रेखाओं AB और DC के बीच स्थित हैं (यद्यपि इनमें उभयनिष्ठ आधार DC है और ये समांतर रेखाओं AD और BC के बीच स्थित है)।
अतः, यह स्पष्ट रूप से ध्यान रखना चाहिए कि दोनों समांतर रेखाओं में से एक उभयनिष्ठ आधार को अंतर्विष्ट करने वाली रेखा होनी चाहिए।
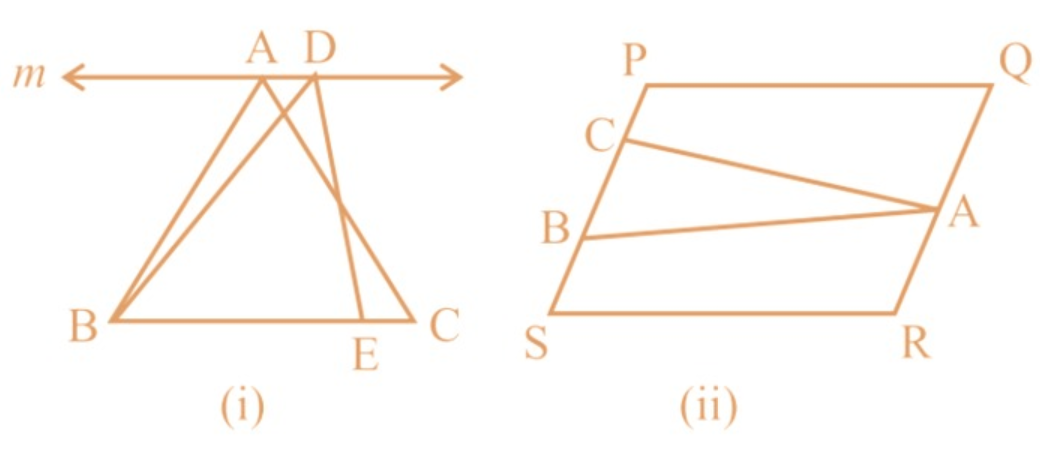
ध्यान दीजिए कि आकृति (i) के ΔABC और ΔDBE उभयनिष्ठ आधार पर स्थित नहीं हैं।
इसी प्रकार, आकृति (ii) के ΔABC और समांतर चतुर्भुज PQRS एक ही आधार पर स्थित नहीं हैं।
उदाहरण 1
निम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित है? ऐसी स्थिति में उभयनिष्ठ आधार और दोनों समांतर रेखाएं लिखिये।
आकृति (i) ΔPDC तथा समलम्ब चतुर्भुज ABCD एक ही आधार DC तथा एक ही समांतर रेखाओं AB और DC के बीच स्थित है
आकृति(iii) में ΔTRQ तथा समांतर चतुर्भुज PQRS एक ही आधार RQ तथा एक ही समांतर रेखाओं RQ और SP के बीच स्थित है
आकृति (v) में चतुर्भुज APCD तथा चतुर्भुज ABQD एक ही आधार AD पर तथा एक ही समांतर रेखाओं AD तथा BQ के बीच स्थित है।
एक ही आधार और एक ही समांतर रेखाओं के बीच समांतर चतुर्भुज
आइए अब एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित दो समांतर चतुर्भुजों के क्षेत्रफलों के मध्य एक संबंध, यदि कोई है तो, ज्ञात करने का प्रयत्न करें।
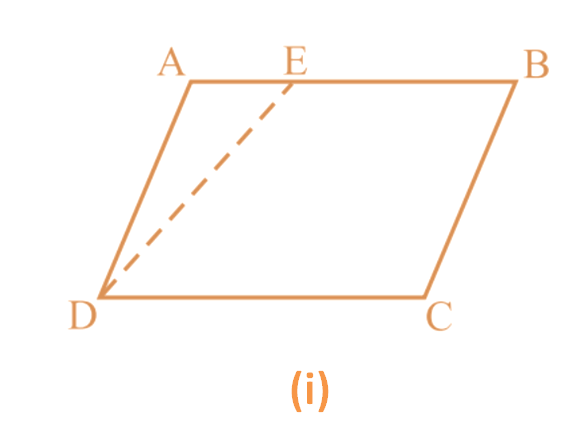
कागज़ की एक मोटी शीट या गत्ते पर एक समांतर चतुर्भुज ABCD खींचिए। अब एक रेखाखंड DE आकृति (i) में दर्शाए अनुसार खींचिए।
अब एक अलग शीट या गत्ते पर एक अन्य कागज की सहायता से त्रिभुज A'D'E' त्रिभुज ADE के सर्वांगसम खींचिए और शीट में से इसे काट लीजिए।
अब ΔA'D'E' को इस प्रकार रखिए कि A'D' भुजा BC के संपाती हो, जैसा कि आकृति (ii) में दर्शाया गया है।
ध्यान दीजिए कि यहाँ दो समांतर चतुर्भुज ABCD और EE'CD हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AE' और DC के बीच स्थित हैं।
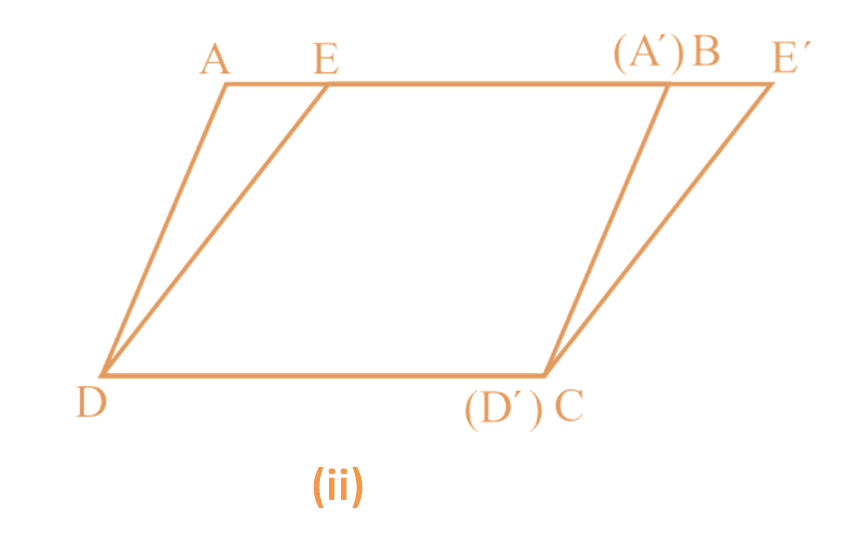
चूंकि ΔADE≅ΔA'D'E'
अतः ar(ADE)=ar(A'D'E')
साथ ही, ar(ABCD)=ar(ADE)+ar(EBCD)
ar(ABCD)=ar(A'D'E')+ar(EBCD)
ar(ABCD)=ar(EE'CD)
अतः दोनों समांतर चतुर्भुज क्षेत्रफल में बराबर हैं।
प्रमेय 1
सिद्ध कीजिए कि एक आधार और एक समांतर रेखाओ के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते है।
दो समांतर चतुर्भुज ABCD और EFCD दिए हुए हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AF और DC के बीच स्थित हैं।
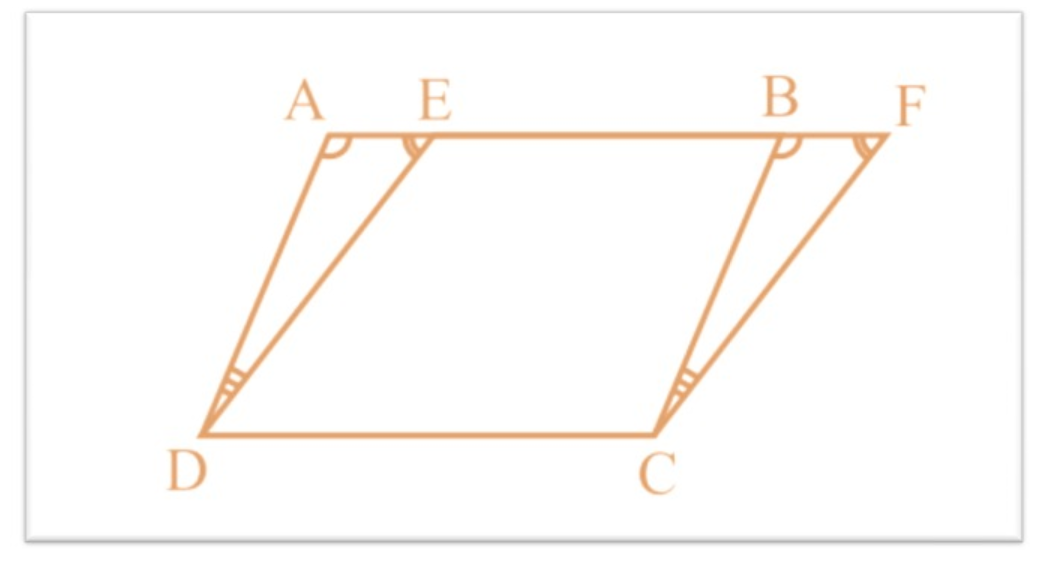
सिद्ध करना है:
ar(ABCD)=ar(EFCD)
ΔADE और ΔBCF में,
∠DAE=∠CBF ....(i)
(AD||BC और तिर्यक रेखा AF से संगत कोण)
∠AED=∠BFC ....(ii)
(ED || FC और तिर्यक रेखा AF से संगत कोण)
इसलिए, ∠ADE=∠BCF ....(iii)
(त्रिभुज का कोण योग गुण)
साथ ही, AD=BC ....(iv)
(समांतर चतुर्भुज की सम्मुख भुजाएँ)
अतः, △ADE≅△BCF
[ASA नियम तथा (i), (iii) और (iv) द्वारा]
इसलिए,
ar (ADE)=ar(BCF)...(v)
(सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं)
अब, ar (ABCD)
=ar(ADE) + ar(EDCB)
=ar(BCF)+ar(EDCB)[समी (v) से]
=ar(EFCD)
ar(ABCD)=ar(EFCD)
अतः, समांतर चतुर्भुज ABCD और EFCD क्षेत्रफल में बराबर हैं।
उदाहरण 2
चित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही AL⊥DC, तो सिद्ध कीजिए कि
(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL
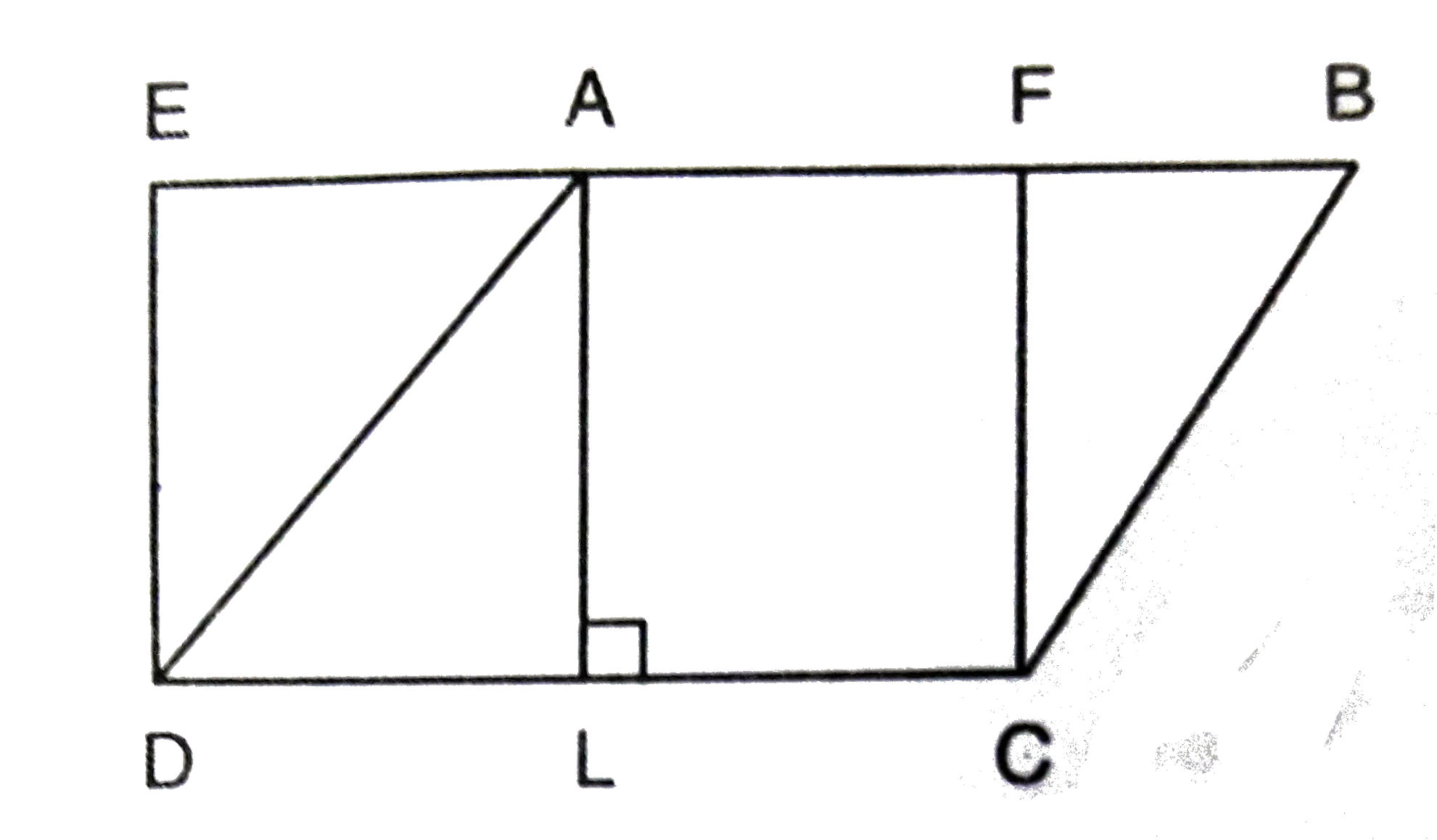
(i) हम जानते है कि आयत भी एक समान्तर चतुर्भुज है
अतः समान्तर चतुर्भुज ABCD तथा आयत EFCD एक ही आधार CD तथा समान समांतर रेखाओं CD तथा BE के बीच में स्थित है।
∴ar(ABCD)=ar(EFCD)
(ii) चूंकि ar(ABCD)=ar(EFCD)
⇒ar(ABCD)=CD×FC
[∴ आयत का क्षेत्रफल =आधार × ऊँचाई ]
⇒ar(ABCD)=CD×AL
[ चूंकि AL=FC क्योंकि ALCF एक आयत है ]
⇒ar(ABCD)=DC×AL
उदाहरण 3
यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओ के बीच स्थित हो, तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
मान लीजिए ΔABP और समांतर चतुर्भुज ABCD एक ही आधार AB और एक ही समांतर रेखाओं AB और PC के बीच स्थित हैं (देखिए आकृति )
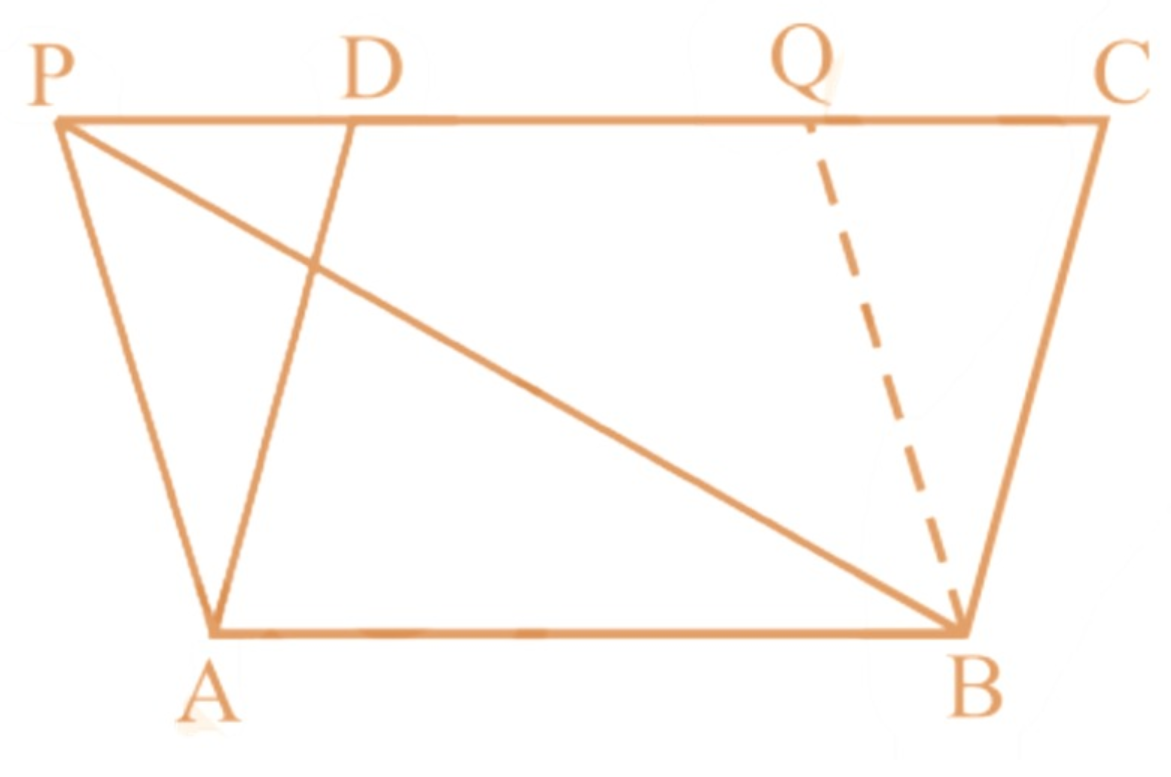
सिद्ध करना है-
ar(PAB)= 12ar(ABCD)
एक अन्य समांतर चतुर्भुज ABQP प्राप्त करने के लिए, BQ||AP खींचिए।
अब समांतर चतुर्भुज ABQP और ABCD एक ही आधार AB और एक ही समांतर रेखाओं AB और PC के बीच स्थित हैं।
अतः
ar(ABQP)=ar(ABCD)...(i)
[प्रमेय 1 से (एक आधार और एक समांतर रेखाओ के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते है)]
परंतु ΔPAB≅ΔBQP
(विकर्ण PB समांतर चतुर्भुज ABQP को दो सर्वांगसम त्रिभुजों में बाँटता है)
⇒ ar(PAB)=ar(BQP)
या ar(PAB)=12ar(ABQP)...(ii)
अतः समी (i) और (ii) से
ar(PAB)=12ar(ABCD)
एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज
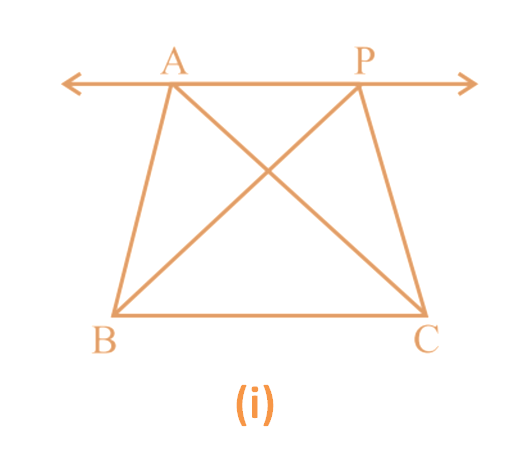
आकृति (i) को देखें। इसमें आप दो त्रिभुज ABC और PBC ऐसे देखेंगे जो एक ही आधार BC और एक ही समांतर रेखाओं BC और AP के बीच स्थित हैं। ऐसे त्रिभुजों के क्षेत्रफलों के बारे में आप क्या कह सकते हैं?
इस प्रश्न का एक तर्कसंगत उत्तर प्राप्त करने के लिए, आप निम्न प्रकार आगे बढ़ सकते हैं:
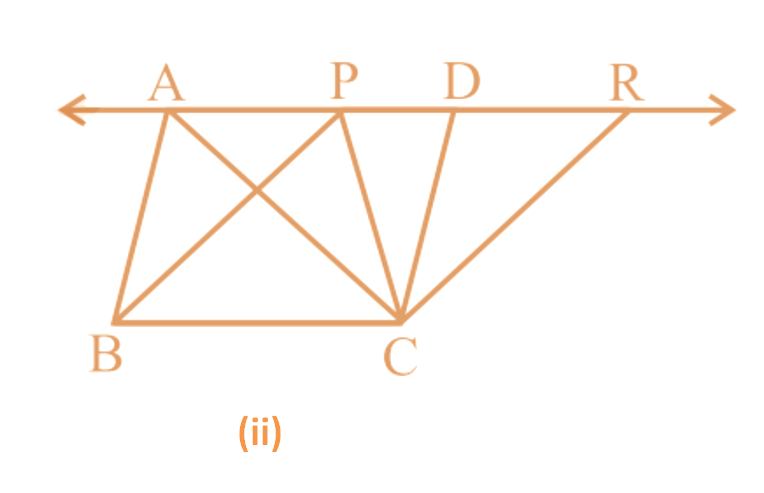
आकृति (ii)में,
CD||BA और CR||BP इसप्रकार खींचिए कि D और R रेखा APपर स्थित हों (देखिए आकृति ii)।
इससे आप दो समांतर चतुर्भुज PBCR और ABCD प्राप्त करते हैं, जो एक ही आधार BC और एक ही समांतर रेखाओं BC और AR के बीच स्थित है।
अब, ar(ABCD)=ar(PBCR) (प्रमेय 1 से)
ΔABC≅ΔCDA और
ΔPBC≅ΔCRP
[समांतर चतुर्भुज का विकर्ण समांतर चतुर्भुज को दो सर्वांगसम त्रिभुजों में बांटता है]
अतः ar(ABC)=12ar(ABCD)और
ar(PBC)=12ar(PBCR)
[एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओ के बीच स्थित हो, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।]
ar(ABC)=ar(PBC)
अतः, इसलिए, इस प्रकार, आप निम्न प्रमेय पर पहुँच गए हैं।
प्रमेय 2
एक ही आधार ( या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल बराबर होते हैं।
ΔABC और ΔDBC एक ही आधार BC पर तथा एक ही समांतर रेखाओं BC तथा EF के बीच स्थित हैं।
सिद्ध करना है:
ar(△ABC)=ar(△DBC)
रचना: CE||BA तथा BF||CD खींचा।
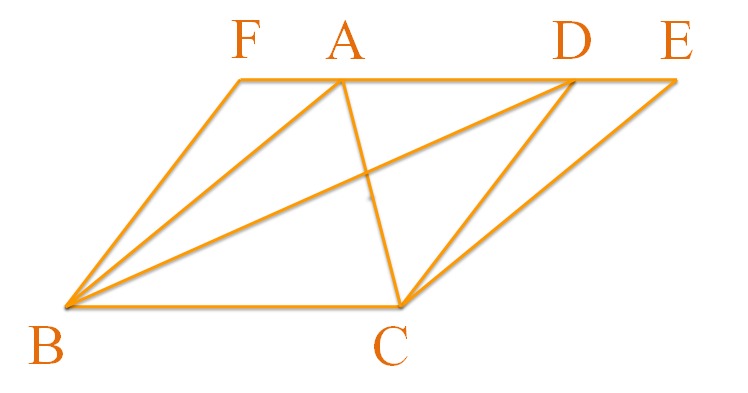
प्रमाण: ABCE एक समांतर चतुर्भुज है। तथा FBCD भी एक समांतर चतुर्भुज है।
चूँकि समांतर चतुर्भुज ABCE तथा समांतर चतुर्भुज FBCD एक ही आधार BC पर और एक ही समांतर रेखाओं के बीच स्थित हैं।
∴ar(ABCE)=ar(FBCD) ...(i)
लेकिन समांतर चतुर्भुज ABCE का विकर्ण AC है
∴ar(ΔABC)=ar(ΔACE)
ar(ΔABC)=12ar(ABCE)....(ii)
इसी प्रकार हम साबित कर सकते हैं कि
ar(ΔDBC)=12(FBCD)....(iii)
(i), (ii) तथा (iii) से
ar(ΔABC)=ar(ΔDBC)
यही सिद्ध करना था।
त्रिभुज का क्षेत्रफल
मान लीजिए ABCD एक समांतर चतुर्भुज है जिसका एक विकर्ण AC है (देखिए आकृति)।
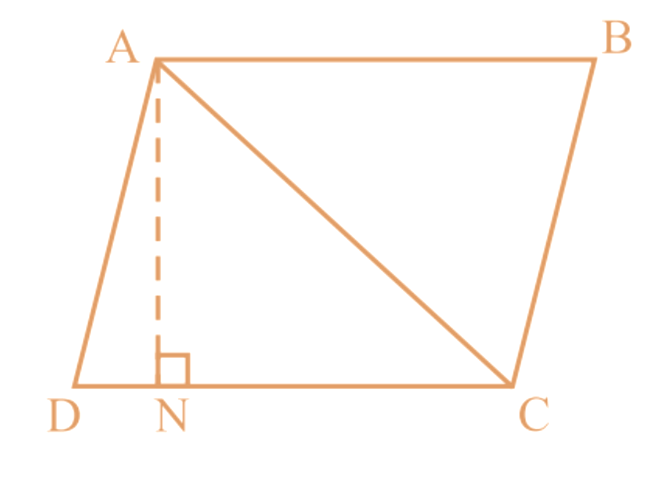
आइए मान लें कि AN⊥DC है। ध्यान दीजिए कि
ΔADC≅ΔCBA
[समांतर चतुर्भुज का विकर्ण समांतर चतुर्भुज को दो सर्वांगसम त्रिभुजों में बांटता है]
अतः,ar(ADC)=ar(CBA)
इसलिए,
ar(ADC)=12ar(ABCD)
=12⋅(DC×AN)
[चूंकि समांतर चतुर्भुज का क्षेत्रफल
= आधार × ऊंचाई ]
अत:, ΔADC का क्षेत्रफल
=12× आधार DC× संगत शीर्षलम्ब AN
दूसरे शब्दों में,
किसी त्रिभुज का क्षेत्रफल उसके आधार (एक भुजा) और संगत शीर्षलम्ब (या ऊँचाई) के गुणनफल के आधे के बराबर होता है।
उदाहरण 4
दिए गए चित्र में ABCD एक चतुर्भुज है और BE||AC इस प्रकार है कि BE बढ़ाई गई DC को E पर मिलती है |दर्शाइए की त्रिभुज ADE का क्षेत्रफल चतुर्भुज ABCD के क्षेत्रफल के बराबर है|
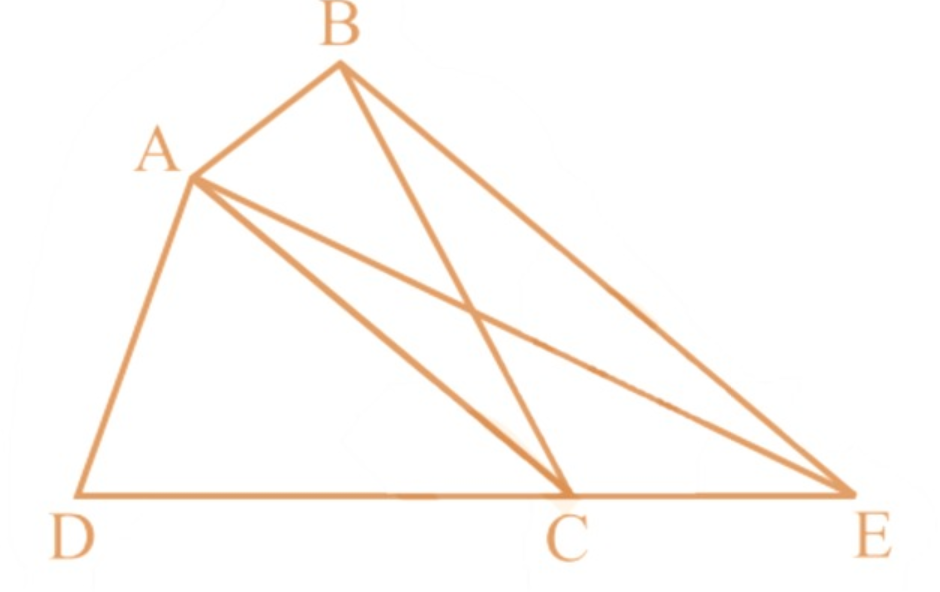
ΔBAC और ΔEAC एक ही आधार AC और एक ही समांतर रेखाओं AC और BE के बीच स्थित है|
अतः ar(BAC)=ar(EAC)
[ प्रमेय से ]
∴ ar(BAC)+ar(ADC)
=ar(EAC)+ar(ADC)
[ दोनों तरफ ar(ADC) जोड़ने पर ]
⇒ar(ABCD)=ar(ADE)
उदाहरण 5
दर्शाइए कि त्रिभुज की एक मध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
माना एक त्रिभुज ABC है जिसके शीर्ष A से आधार BC पर एक मध्यिका AD खींची गई है।
∴BD=DC
सिद्ध करना है :
ar(ABD)=ar(ADC)
रचना :
शीर्ष A से गुजरती हुई एक रेखा l खींची जो BC के समांतर है।
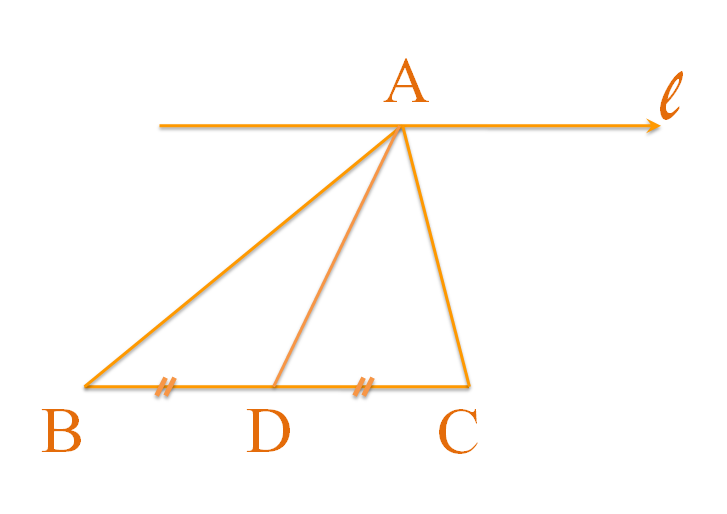
चूंकि एक ही आधार ( या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल बराबर होते हैं।
यहाँ बराबर आधार BD और DC हैं तथा एक ही समांतर रेखा l है।
∴ar(ABD)=ar(ADC)
उदाहरण 6
ΔABC में D भुजा AB का मध्य बिंदु है तथा P,BC पर कोई बिंदु है CQ||PD,AB के बिंदु Q पर मिलती है। सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
रचना : CD को मिलायें।
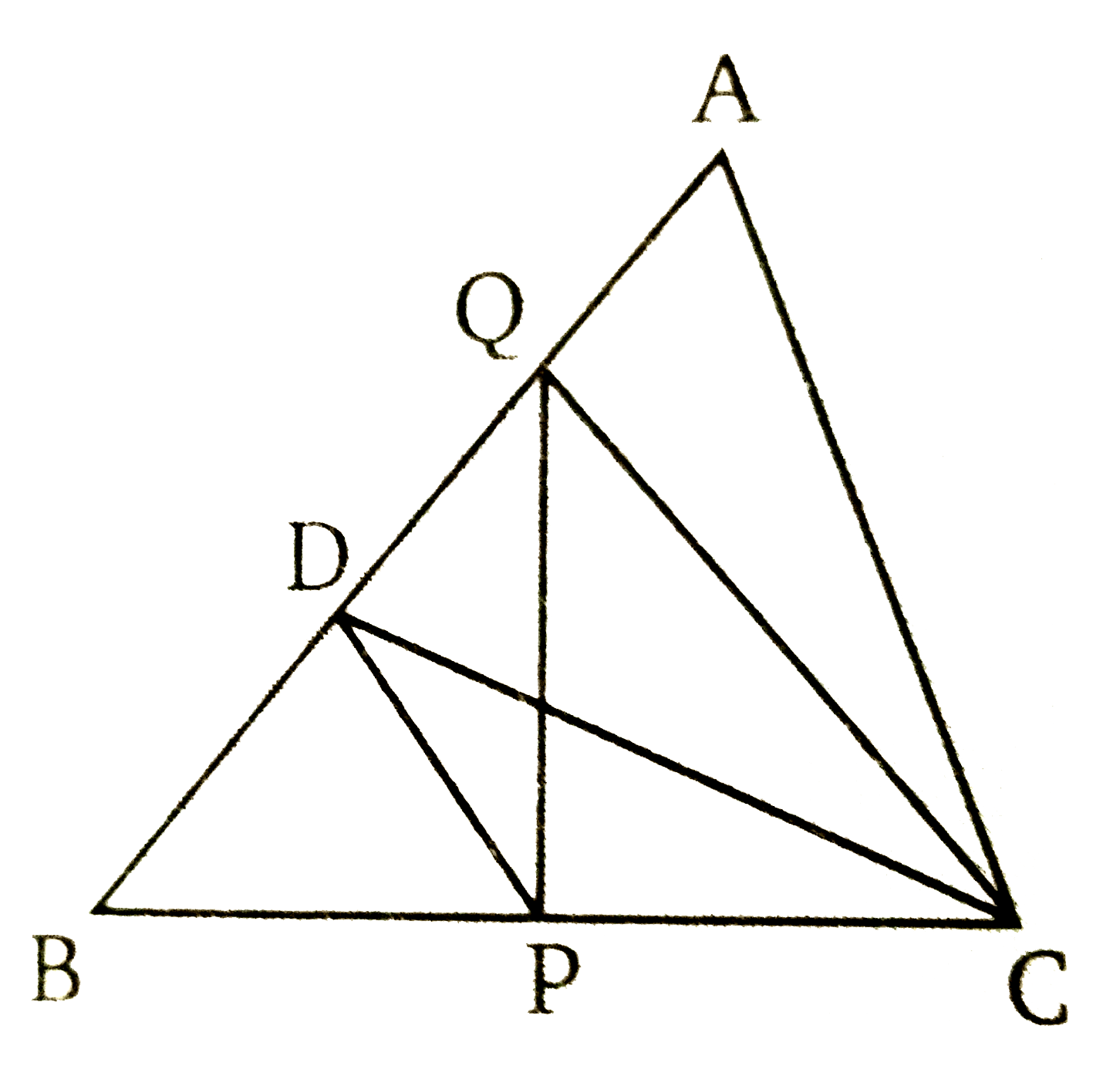
उपपत्ति : क्योंकि D भुजा AB का मध्य बिंदु है।
∴ΔABC में CD माध्यिका है इसलिए
ar(ΔBCD)=12ar(ΔABC)....(i)
चूंकि ΔPDQ व ΔPDC समान आधार PD व समान समांतर रेखाओें PD व QC के बीच हैं।
ar(ΔPDQ)=ar(ΔPDC)…(ii)
समीकरण (i) से
ar(ΔBCD)=12ar(ΔABC)
(ΔBPD)+ar(ΔPDC)=12ar(ΔABC)
ar(ΔBPD)+ar(ΔPDQ)=12ar(ΔABC)
[समीकरण (ii) से]
अतः ar(ΔBPQ)=12ar(ΔABC)
प्रमेय 3
एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
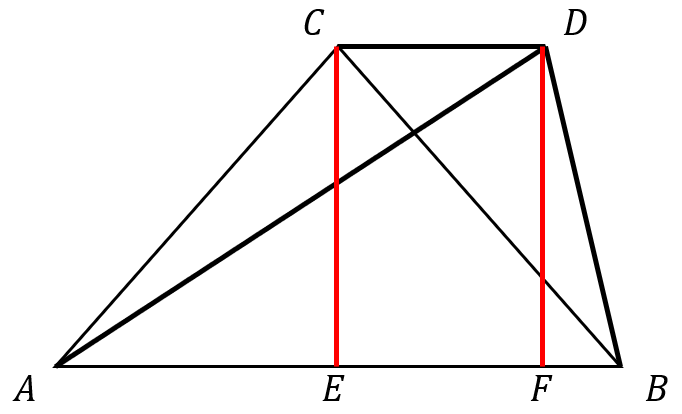
दिया है,
△ABC व △ADB एक ही आधार AB पर पर बने दो त्रिभुज है,
जहाँ ar(ABC)=ar(ADB) है
सिद्ध करना है - AB∣∣CD
रचना - CE⊥AB तथा DF⊥AB
हम जानते हैं कि एक ही रेखा पर डाले गए दो लंब परस्पर समांतर होते है
CE∣∣DF
ar(△ABC)=12×AB×CE
ar(△ADB)=12×AB×DF
चूंकि ar(△ABC)=ar(△ADB)
⇒12×AB×CE=12×AB×DF
⇒CE=DF
चतुर्भुज EFDC में
CE∣∣DF
CE=DF
चूंकि जिस चतुर्भुज का कोई एक भी सम्मुख भुजा का युग्म बराबर और समांतर हो तो वह चतुर्भुज समांतर चतुर्भुज होता है।
अतः EFDC एक समांतर चतुर्भुज है
EF∣∣CD
अतः AB∣∣CD (चूंकि EF रेखाखण्ड AB का एक भाग है।)
उदाहरण 7
आकृति में, क्षेत्रफल (DRC) = क्षेत्रफल (DPC) है और क्षेत्रफल (BDP) = क्षेत्रफल (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब हैं।
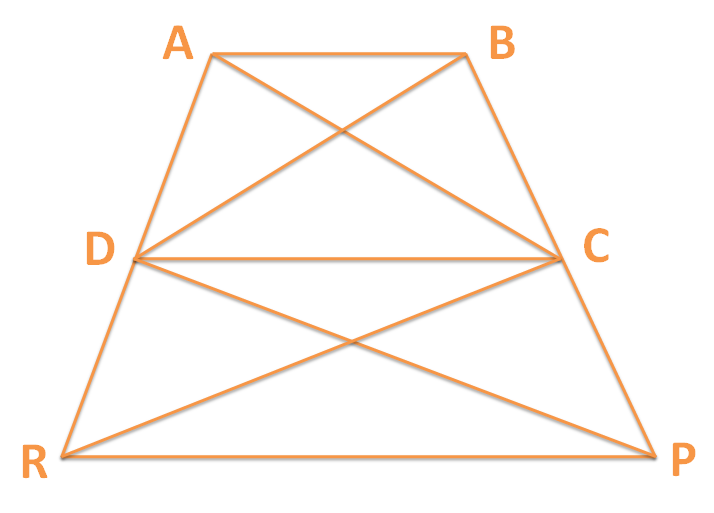
दिया है :
ar(DRC)=ar(DPC)....(i) और
ar(ARC)=ar(BDP)....(ii)
समी (ii)− समी (i)
ar(ARC)−ar(DRC)=ar(BDP)−ar(DPC)
ar(ADC)=ar(BDC)....(iii)
ΔADC और ΔBDC एक ही आधार DC पर हैं और इनका क्षेत्रफल भी बराबर है [ समी (iii) ]।
चूंकि एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
∴DC||AB
अब चतुर्भुज ABCD में,
चूंकि DC||AB
∴ABCD एक समलंब चतुर्भुज है।
ΔDRC और ΔDPC एक ही आधार DC पर हैं और इनका क्षेत्रफल भी बराबर दिया है [ समी (i) ]।
चूंकि एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
∴DC||RP
अब चतुर्भुज DCPR में,
चूंकि DC||RP
∴DCPR एक समलंब चतुर्भुज है।
सारांश
इस अध्याय में आपने निम्नलिखित बिन्दुओं का अध्ययन किया है :
1. एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (किसी मात्रक में) एक संख्या होती है।
2. दो सर्वागसम आकृतियों के क्षेत्रफल बराबर होते हैं, परन्तु इसका विलोम आवश्यक रूप से सत्य नहीं है।
3. यदि एक आकृति T द्वारा निर्मित कोई तलीय क्षेत्र किन्हीं दो आकृतियों P और Q द्वारा दो अनातिव्यापी तलीय क्षेत्रों से मिल कर बना है, ar(T)=ar(P)+ar(Q) है, जहाँ ar(X) आकृति X का क्षेत्रफल व्यक्त करता है।
4. दो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनमें एक उभयनिष्ठ आधार (एक भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
5. एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
6. समांतर चतुर्भुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब का गुणनफल होता है।
7. एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
8. यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
9. एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
10. त्रिभुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब के गुणनफल का आधा होता है।
11. एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
12. त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
