त्रिभुज कक्षा 9 गणित
भूमिका
पिछली कक्षाओं में, त्रिभुजों और उनके विभिन्न गुणों के बारे में हम पढ़ चुके हैं। तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बंद आकृति (closed figure) एक त्रिभुज (triangle) कहलाती है ('त्रि' का अर्थ है 'तीन')। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। उदाहरणार्थ, आकृति में दिए त्रिभुज ABC, जिसे △ABC से व्यक्त करते हैं, की तीन भुजाएँ AB,BC और CA हैं, ∠A,∠B और ∠C इसके तीन कोण हैं तथा A,B और C इसके तीन शीर्ष हैं।
पिछली कक्षा में त्रिभुजों के कुछ गुणों का भी अध्ययन कर चुके हैं। इस अध्याय में, त्रिभुजों की सर्वांगसमता (congruence), सर्वांगसमता के नियमों, त्रिभुजों के कुछ अन्य गुणों और त्रिभुजों में असमिकाओं (inequalities) के बारे में विस्तृत रूप से अध्ययन करेंगे।
आइये जानते है त्रिभुज को और करीब से....
बच्चों आप कक्षा 7 में, त्रिभुजों और उनके विभिन्न गुणों के बारे में अध्ययन कर चुके हैं। आप जानते हैं कि तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बंद आकृति (closed figure) एक त्रिभुज(triangle) कहलाती है ('त्रि' का अर्थ है 'तीन')। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं।अध्याय 6 में, आप त्रिभुजों के कुछ गुणों का भी अध्ययन कर चुके हैं। इस अध्याय में, आप त्रिभुजों की सर्वांगसमता (congruence), सर्वांगसमता के नियमों, त्रिभुजों के कुछ अन्य गुणों और त्रिभुजों में असमिकाओं (inequalities) के बारे में विस्तृत रूप से अध्ययन करेंगे।
त्रिभुजों की सर्वांगसमता
सर्वांगसमता - बच्चों सबसे पहले हम सर्वांगसमता को समझते हैं की ये होती क्या है ? फिर हम त्रिभुजों की सर्वांगसमता के बारे में बात करेंगें | तो बच्चों आपने ये जरूर देखा होगा कि आपकी फोटो की एक ही साइज की दो कॉपियां एक जैसी (identical) होती हैं। इसी प्रकार, एक ही माप की दो चूड़ियाँ और एक ही बैंक द्वारा जारी किए गए दो एटीएम(ATM) कार्ड एक जैसे होते हैं। ये सर्वांगसम आकृतियाँ (congruent figures) कहलाती हैं ('सर्वांगसम' का अर्थ है 'सभी प्रकार से बराबर' अर्थात वे आकृतियाँ जिनके समान आकार और समान माप हैं)। आपने अपने रेफ्रीजरेटर में बर्फ की ट्रे (ice tray) अवश्य ही देखी होगी। ध्यान दीजिए कि बर्फ जमाने के लिए बने सभी खाँचे सर्वांगसम हैं। ट्रे में (खाँचों के लिए प्रयोग किए गए साँचों की गहराइयाँ भी सर्वांगसम होती हैं (ये सभी आयताकार या सभी वृत्ताकार या सभी त्रिभुजाकार हो सकते हैं)। अतः, जब भी सर्वसम (एक जैसी) वस्तुएँ बनानी होती हैं, तो साँचे बनाने के लिए सर्वांगसमता की संकल्पना का प्रयोग किया जाता है।अब एक ही त्रिज्या के दो वृत्त लेते हैं और एक को दूसरे पर रखिए। आप क्या देखते हैं? ये एक दूसरे को पूरी तरह से ढक लेते हैं और हम इन्हें सर्वांगसम वृत्त कहते हैं।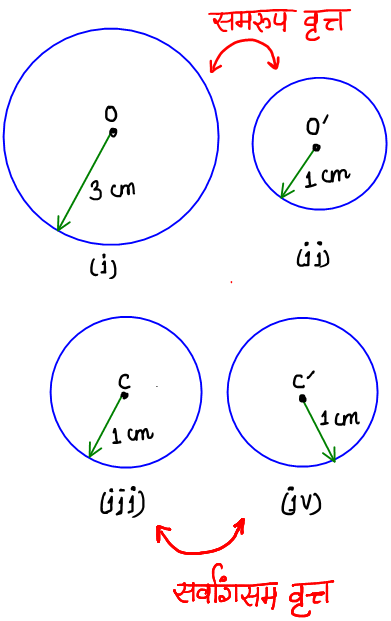
इसी प्रकार दो समान भुजाओ वाले वर्ग भी सर्वांगसम आकृतियाँ हैं |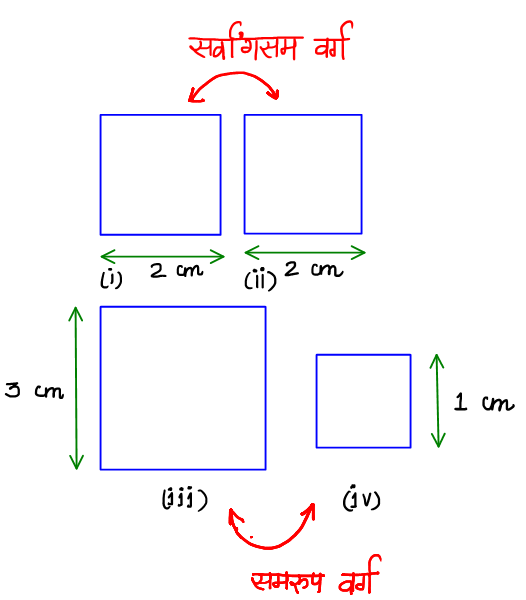
आइये अब दो त्रिभुजों की सर्वांगसमता के बारे में बात करते हैं |
त्रिभुजों की सर्वांगसमता : आप पहले से ही जानते हैं की दो त्रिभुज सर्वांगसम तब होते हैं जब एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों |
आकृति देखिये 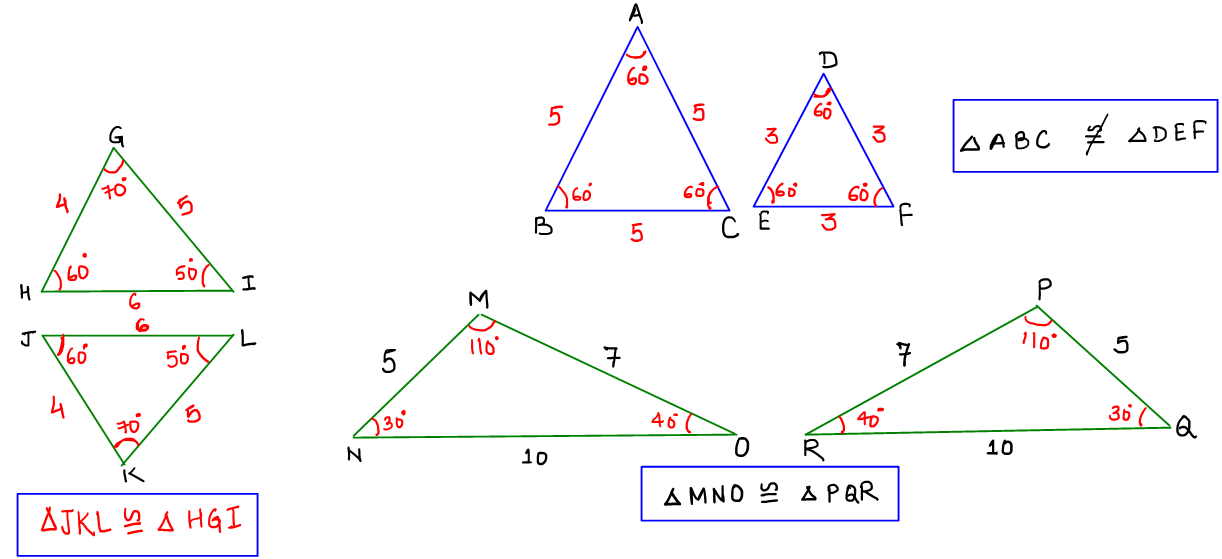
अब उपर्युक्त आकृति में देखिये की त्रिभुज ABC तथा त्रिभुज DEF के संगत कोण बराबर हैं परन्तु इनकी संगत भुजाएँ बराबर नहीं हैं | इसलिए ये दोनों त्रिभुज एक दूसरे को पूरी तरह ढक नहीं पाएंगे और इसीलिए ये दोनों त्रिभुज सर्वांगसम नहीं हैं | अब त्रिभुज GHI और त्रिभुज JKL की बात करते हैं इनमे ये खासियत है कि इनके संगत कोण तथा संगत भुजाएँ दोनों क्रमशः बराबर हैं (उपर्युक्त आकृति में देखिये ) तो अब ये दोनों त्रिभुज एक दूसरे को पूरी तरह से ढक लेंगें और इस प्रकार दोनों त्रिभुज एक दूसरे के सर्वांगसम हैं ठीक इसी प्रकार से त्रिभुज MNO एवं त्रिभुज PQR भी सर्वांगसम हैं |
अब बात आती है जब दो त्रिभुज सर्वांगसम होते हैं तब उन्हें सांकेतिक रूप में लिखते कैसे हैं ? बच्चों सर्वांगसमता का चिन्ह ≅ होता है इसलिए जब दो त्रिभुज सर्वांगसम है तब इसे हम निम्न प्रकार लिखते है जैसे ऊपर की आकृति में त्रिभुज GHI और त्रिभुज JKL सर्वांगसम हैं तो
△GHI≅△JKL
जैसा की हम जानते है दो त्रिभुज सर्वांगसम होंगे यदि एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों। इस प्रकार यदि दो त्रिभुज सर्वांगसम हो तब सर्वांगसम त्रिभुजों में संगत भाग बराबर होते हैं और "सर्वांगसम त्रिभुजों के संगत भागों के लिए" हम संक्षेप में "CPCT" (Corresponding parts of congruent triangle) लिखते हैं।
OMR (One Minute Revision)
अलग अलग भुजाओ वाले वर्ग , अलग अलग त्रिज्याओं वाले वृत्त ये सभी सर्वांगसम आकृतियाँ नहीं होती है। जैसे उपर्युक्त आकृति में 3 cm और 1 cm वाले वर्ग तथा 3 cm एवं 1 cm त्रिज्या वाले वृत्त ये सभी सर्वांगसम नहीं हैं जबकि देखने में दोनों वर्ग तथा दोनों वृत्त ही हैं।
अभिगृहीत 1
इस नियम के अनुसार दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।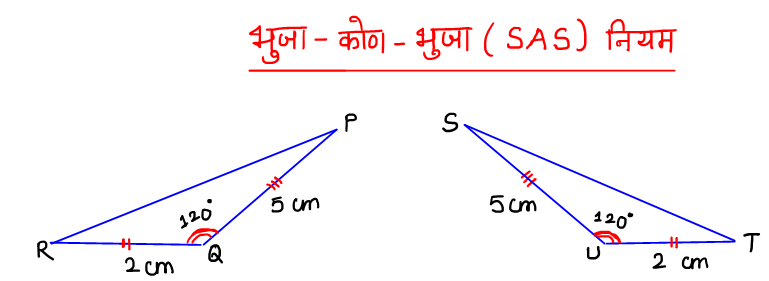
उदाहरण 1
दिय गए आकृति में OA = OB और OD = OC है | दर्शाइए कि
(i) ΔAOD≅ΔBOC और (ii) AD∣∣BC 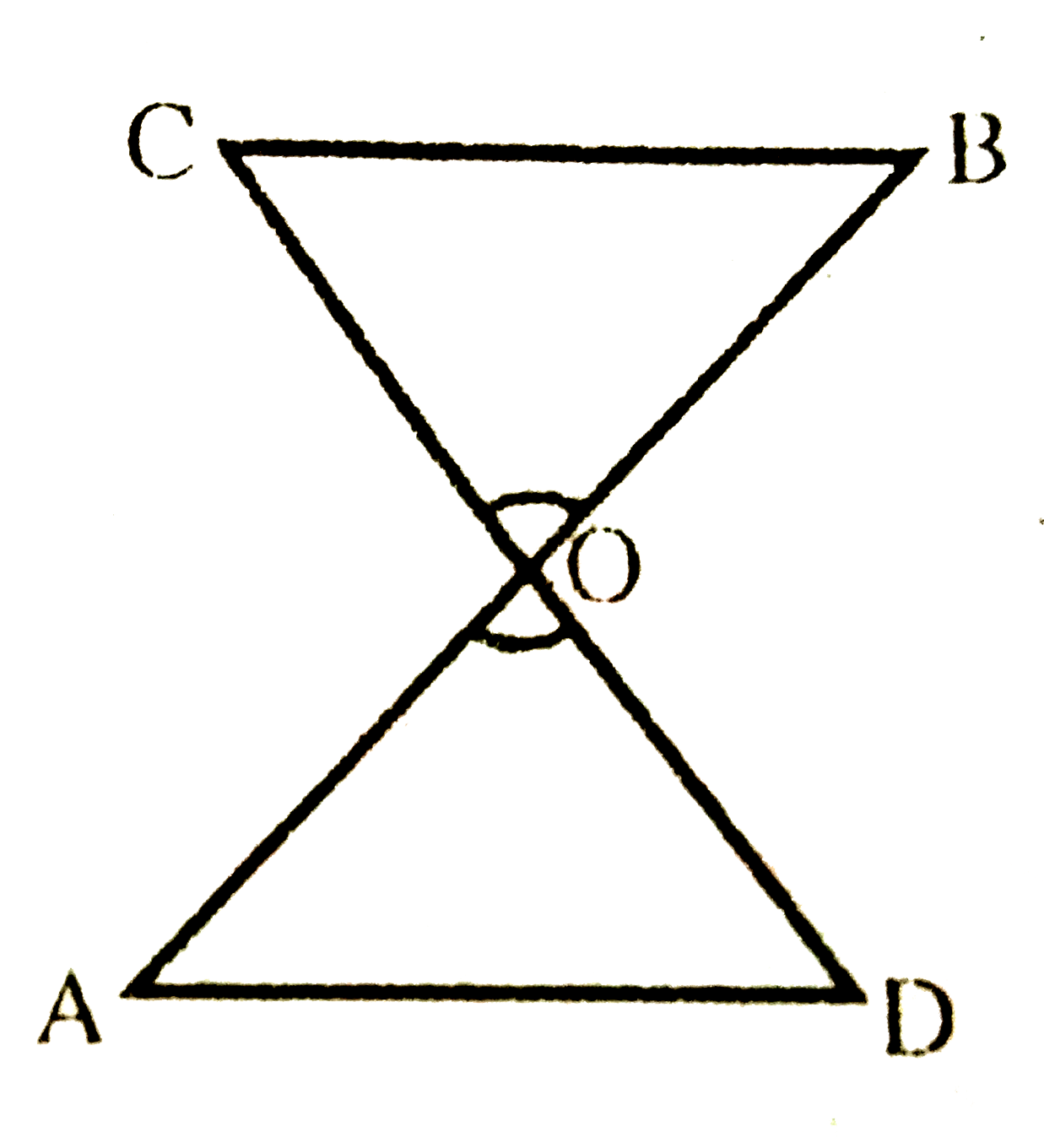
(i) ΔAOD और ΔBOC में,
दिया है
OA=OBOD=OC}
चूँकि ∠AOD और ∠BOC शीर्षाभिमुख कोनों का एक युग्म है,
अत:
∠AOD=∠BOC
इसलिए,ΔAOD≅ΔBOC
[SAS सर्वांगसमता नियम से ]
(ii) सर्वांगसम त्रिभुजों AOD और BOC में, अन्य संगत भाग भी बराबर होंगे |
अत: ∠OAD=∠OBC
परन्तु ये रेखाखंडों AD और BC के लिए एकांतर कोणों का एक युग्म बनाते हैं |
अत:,AD∣∣BC
प्रमेय 7.1
दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हों।
दिया है,
△ABC और △DEF में ∠B=∠E
∠C=∠F और BC=EF
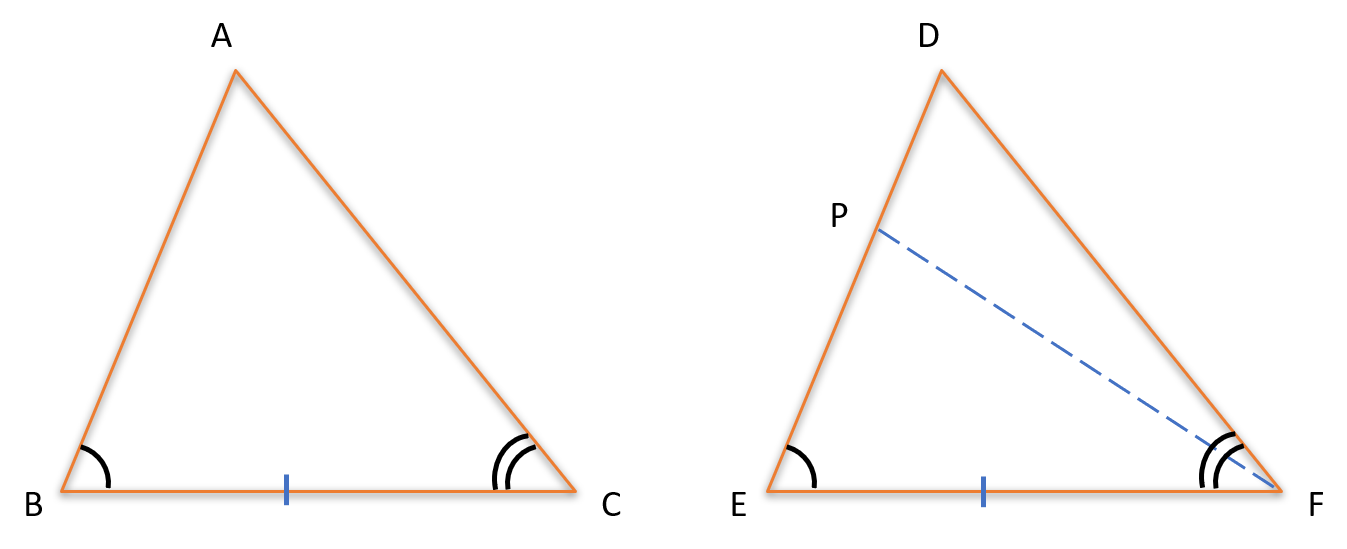
सिद्ध करना है: △ABC≅△DEF
प्रमाण : ΔABC की भुजा AB, ΔDEF की भुजा DE के या तो बराबर या छोटी या बड़ी होगी।
स्थिति (i): यदि AB = DE हो, तो SASअभिगृहीत से ΔABC≅△DEF और इस प्रकार प्रमेय साबित हो जाता है।
स्थिति (ii) : यदि AB<DE तो DE पर ऐसा बिन्दु P लिया कि PE = AB हो । PF को मिलाया । अब ΔABC और ΔPEF में
AB = PE [ माना हुआ है]
BC = EF [दिया है]
∠B=∠E [दिया है]
△ABC≅△PEF [SAS सर्वांगसमता अभिगृहीत]
अत: ∠ACB=∠PFE [CPCT ]
लेकिन ∠ACB=∠PFE [दिया है]
∠PFE= ∠DFE
यह तभी संभव है जब किरण FP किरण FD के संपाती हो अर्थात् बिन्दु P, बिन्दु D के संपाती हो
AB = DE
ΔABC≅ΔDEF
स्थिति (iii) : यदि AB>DE हो तो स्थिति (ii) में दिये गये तर्क से सिद्ध कर सकते हैं
जिस प्रकार DE के मध्य एक बिन्दु P लिया था उसी प्रकार AB के मध्य एक बिन्दु ले सकते है तब पिछले स्थिति (ii) की तरह,
△ABC≅△DEF
अतः सभी स्थितियों में, ΔABC≅△DEF यही साबित करना था।
सर्वांगसमता की इस कसौटी पर आधारित दो सर्वांगसम त्रिभुज निम्न प्रकार से होंगे -
एक त्रिभुज के लिए कुछ गुण
गुण -1 यदि किसी त्रिभुज की दो भुजाएँ बराबर लम्बाई की है तो ऐसे त्रिभुज को समद्विबाहु त्रिभुज कहा जाता है | 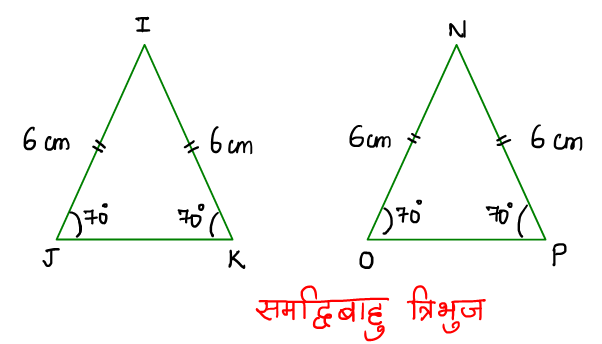
प्रमेय 7.2
एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
दिया है: ΔABC में AB = AC
सिद्ध करना है : ∠B=∠C
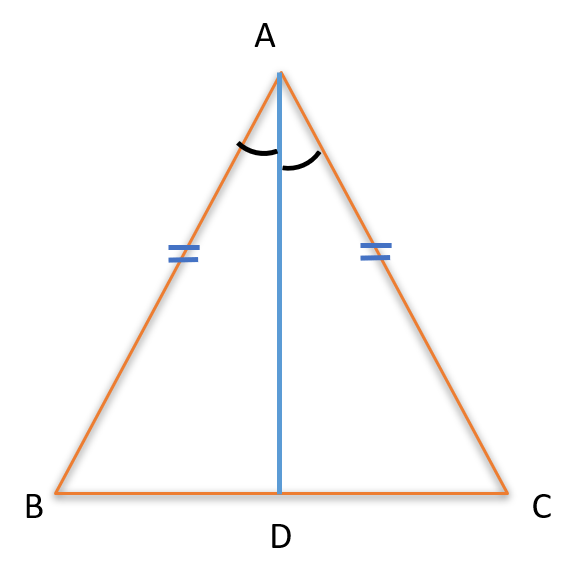
रचना : ∠A का समद्विभाजक AD खींचा जो BC से D पर मिलता है ।
प्रमाण : ΔABD और ΔACD में
AB = AC [दिया है ]
AD = AD [ उभयनिष्ठ ]
∠BAD=∠CAD [रचना से ]
ΔABD≅ΔACD [SAS सर्वांगसमता से ]
अतः ∠B=∠C [CPCT]
प्रमेय 7.3
किसी त्रिभुज के बराबर कोणों की सम्मुख भुजाएं बराबर होती है।
दिया है: ΔABC में ∠B=∠C
सिद्ध करना है : AB=AC
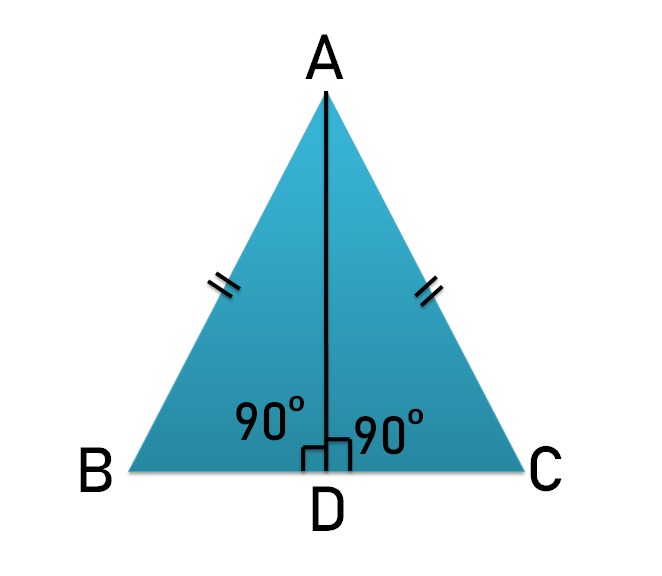
रचना : ∠A का समद्विभाजक AD खींचा जो BC से D पर मिलता है ।
प्रमाण :
△ABDव△ADC में
∠ADB=∠ADC=90∘
AD=AD (उभयनिष्ठ ]
∠B=∠C(दिया हैं )
तब
△ABD≅△ACD [ RHS]
AB=AC [CPCT]
OMR (One Minute Revision)
- एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
- किसी त्रिभुज के बराबर कोणों के सम्मुख कोण बराबर होता है।
उदाहरण 2
चतुर्भुज ABCD में, AC = AD है और AB कोण A को समद्विभाजित करता है (देखिए आकृति) | दर्शाइए कि ΔABC≅ΔABD है |
BC और BD के बारे में आप क्या कह सकते हैं ?
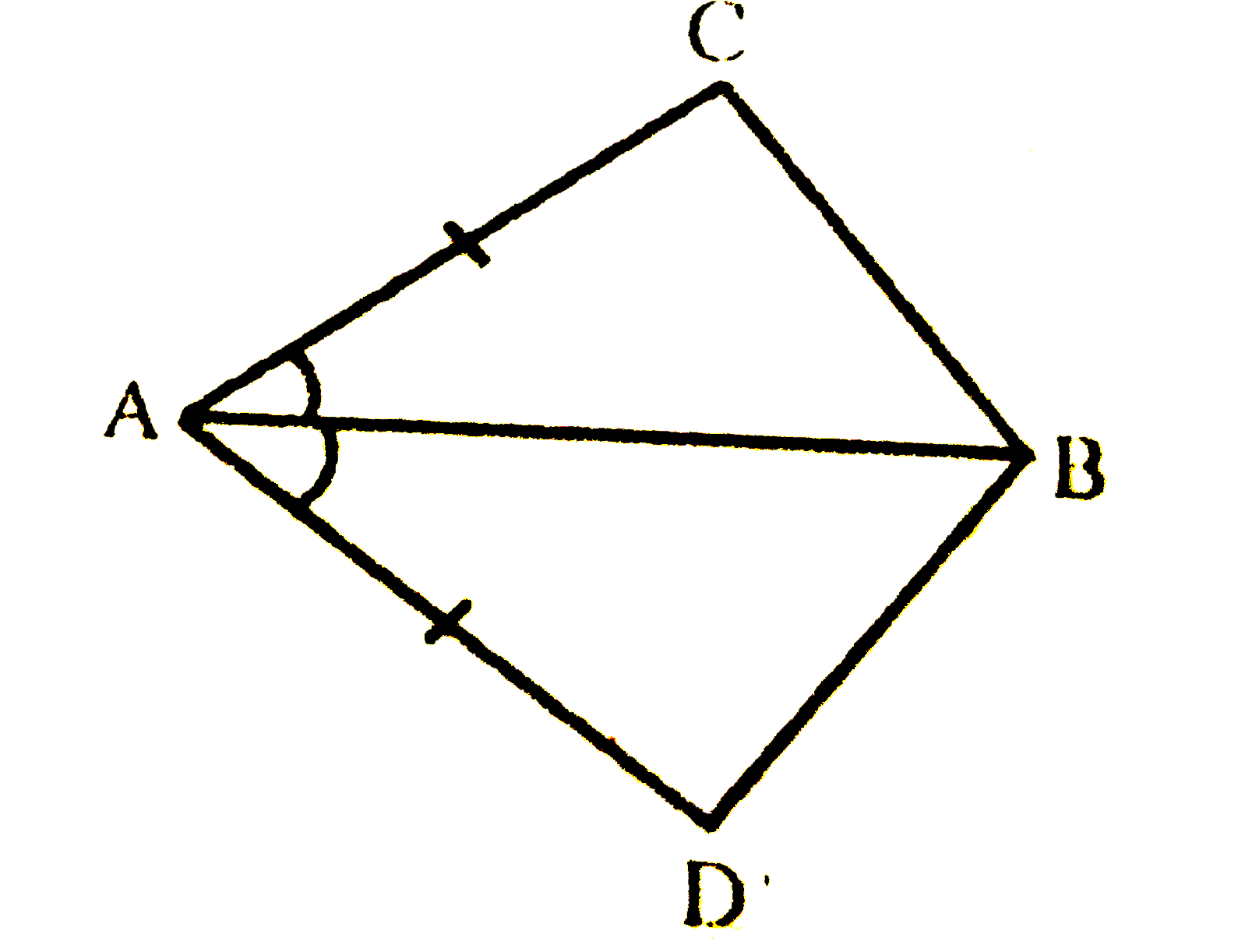
ΔABC तथा ΔABD में
दिया है:
AC=AD
AB=AB
[उभयनिष्ठ]
∠CAB=∠BAD
[ AB ,∠A का अर्धक है]
अत:
ΔABC≅ΔABD
BC=BD
अत: BC और BD बराबर लम्बाई के हैं [CPCT] |
माना,
∠CAB=∠1
∠BAD=∠2 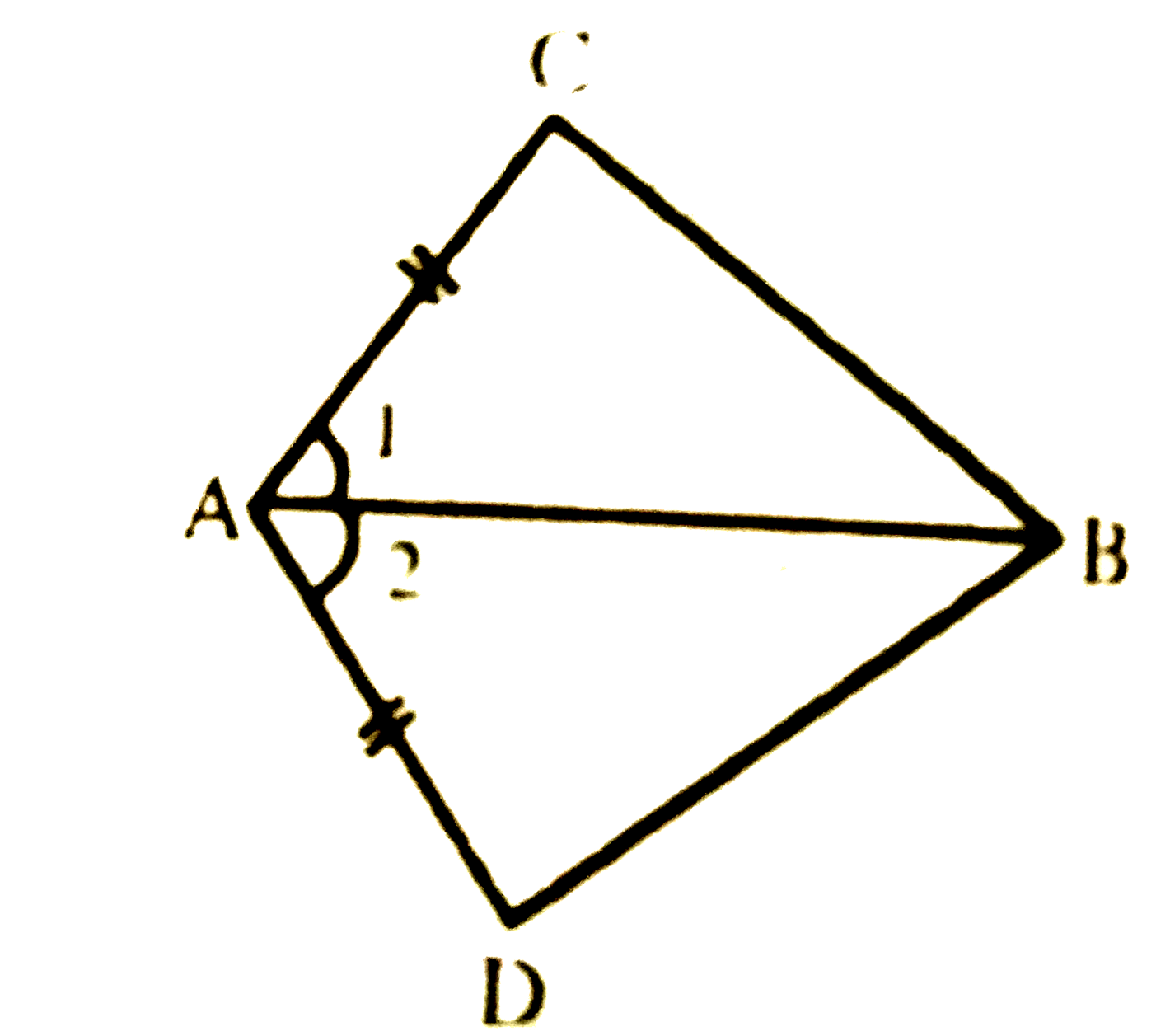
उदाहरण 3
निचे के चित्र में एक रेखाखंड AB पर AD और BC दो बराबर रेखाखंड हैं दर्शाइए कि CD, रेखाखंड AB को समद्विभाजित करता है |
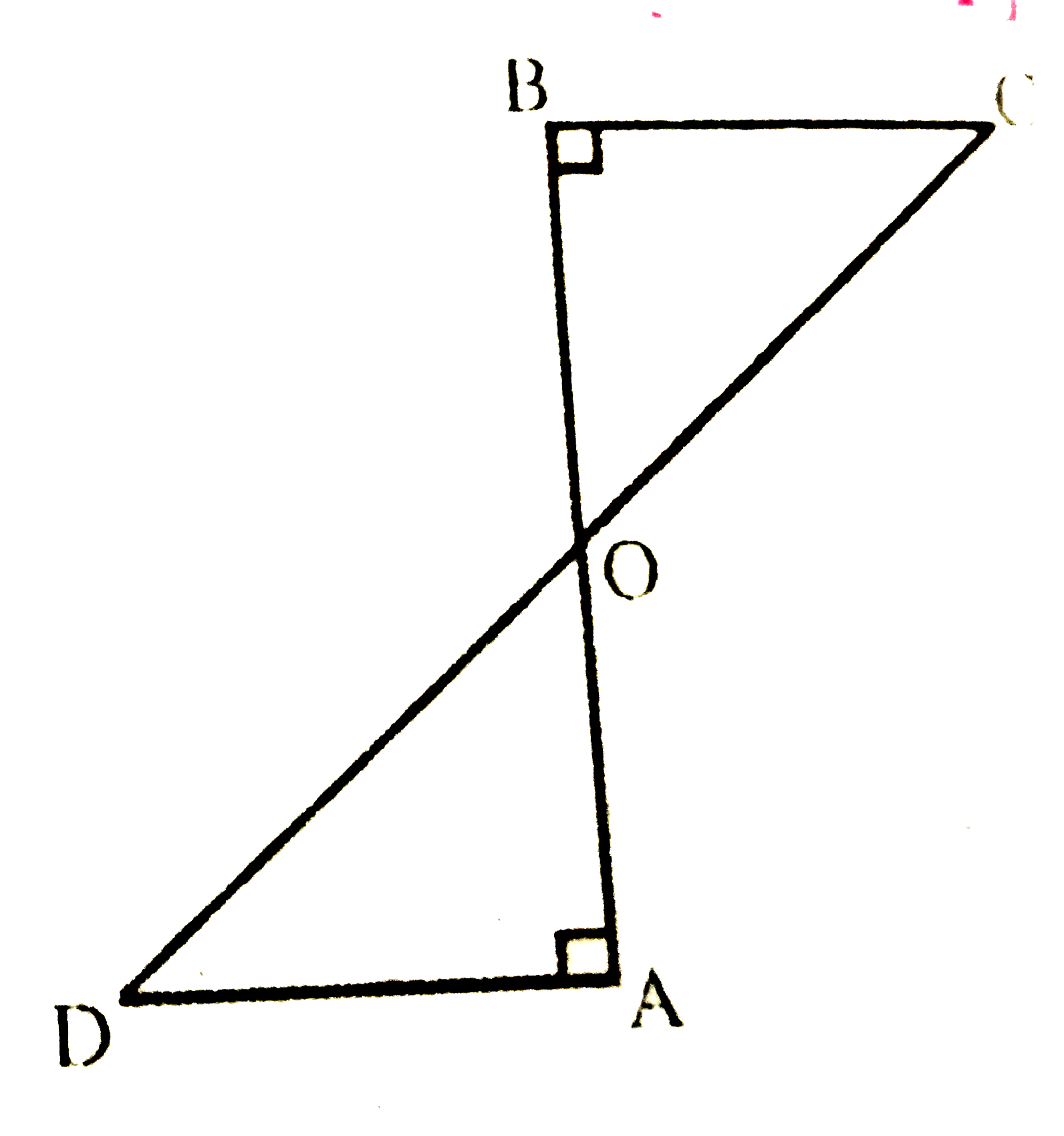
सिद्ध करना है कि
OA = OB
प्रमाण:
ΔOAD और ΔOBC में,
AD=BC [दिया है]
∠OAD=∠OBC
[प्रत्येक =90∘,
चूंकि AB⊥AD तथा AB⊥BC]
∠AOD=∠COB[सम्मुख कोण ]
∴ ΔOAD≅ΔOBC [ AAS सर्वांगसमता नियम से ]
∴ OA=OB
अत: CD, रेखाखण्ड AB को समद्विभाजित करता है |
उदाहरण 4
ΔABC में, ∠A का समद्विभाजक AD भुजा BC पर लम्ब है | दर्शाइए कि AB = AC है और ΔABC समद्विबाहु है |
ΔABD और ΔACD में,
∠BAD=∠CAD[ दिया है ]
AD=AD[ उभयनिष्ठ ]
∠ADB=∠ADC=90∘
[AD⊥BC]
∴ΔABD≅ΔACD
[ ASA सर्वांगसमता नियम ]
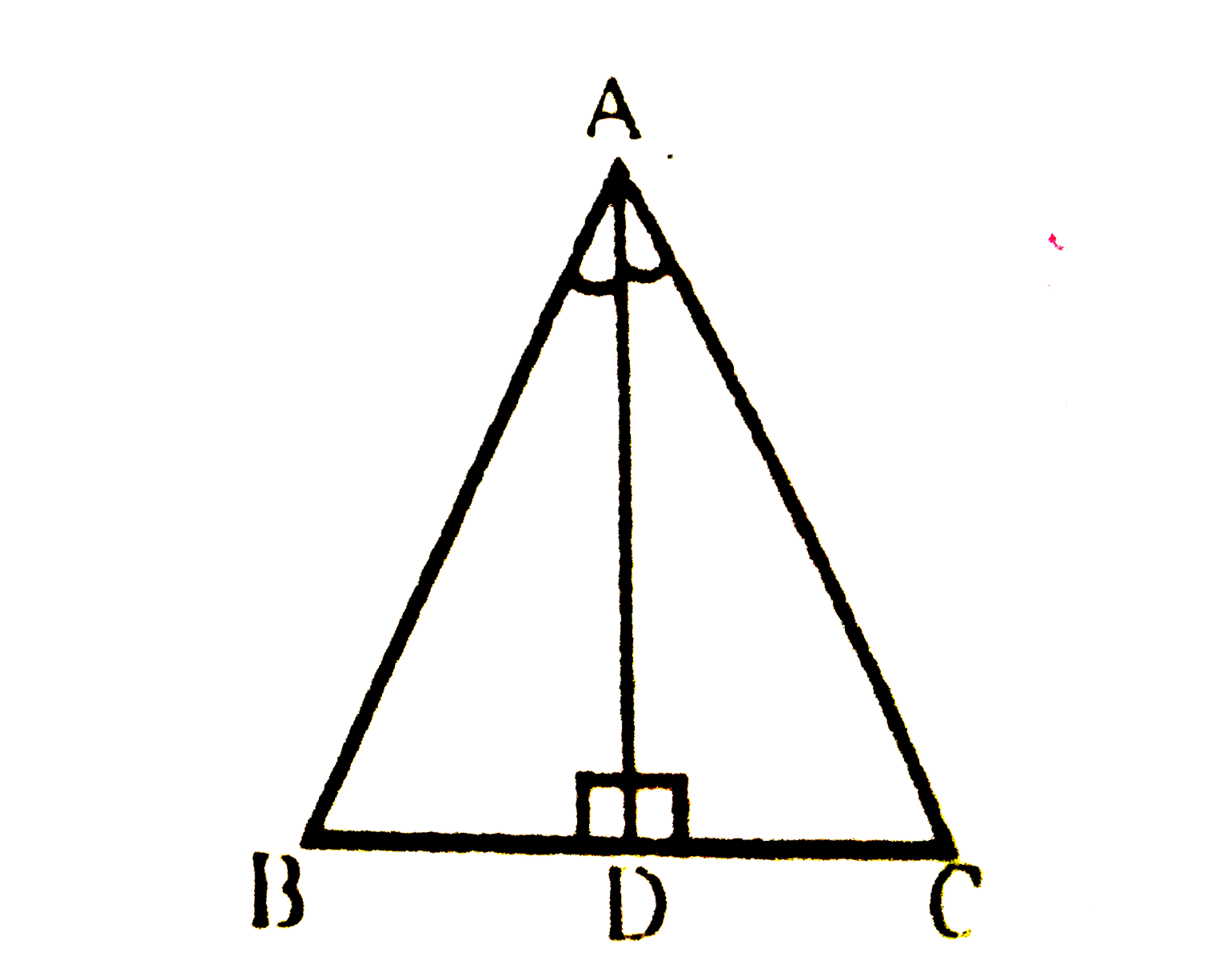
इसलिए, AB=AC
[CPCT]
अत: ΔABC समद्विबाहु है |
उदाहरण 5
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं | RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है |
दिया है :
ABC एक त्रिभुज है जिसमें तथा BE⊥AC तथा CF⊥AB तथा BE=CF
सिद्ध करना है कि
ΔABC समद्विबाहु है अर्थात AB = AC.
प्रमाण :
ΔBEC तथा ΔCFB में,
∠BEC=∠CFB=90∘
BC=BC
[ उभयनिष्ठ ]
तथा BE=CF
[दिया है ]
अत: ΔBEC≅ΔCFB
[RHS सर्वांगसमता नियम से ]
∴ ∠ECB=∠FBC
⇒ ∠C=∠B
⇒ AB=AC
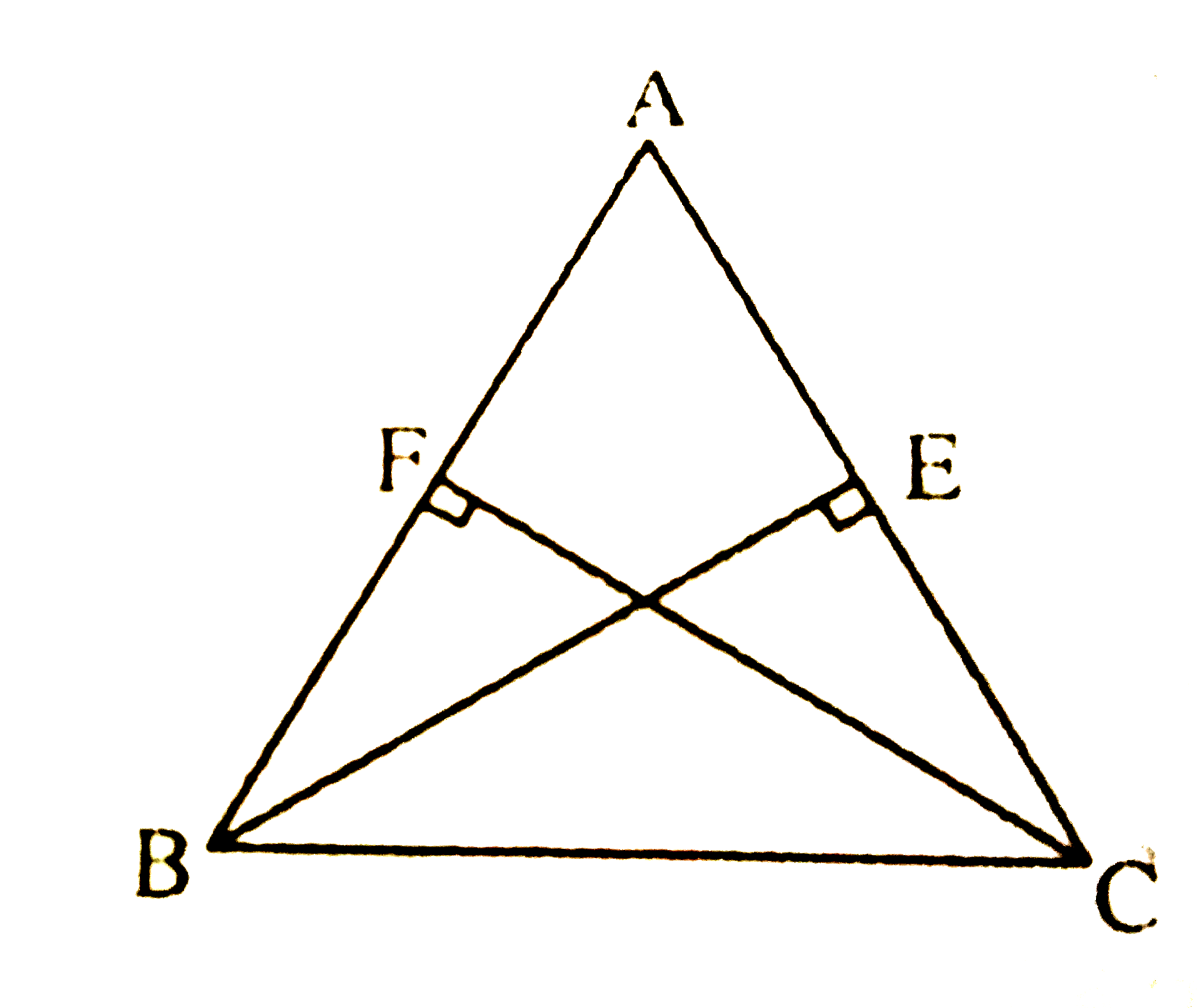
त्रिभुजों की सर्वांगसमता के लिए कसौटियाँ
दोस्तों त्रिभुजों की सर्वांगसमता को सिद्ध करने के लिए हमारे पास 5 नियम है।
आप पहले से यह जानते हैं कि दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों।कक्षा 7 में आप त्रिभुजों की सर्वांगसमता के लिए चार कसौटियाँ (criteria) या नियम (rules) पढ़ चुके हैं। आइए इनका पुनर्विलोकन करें।
भुजा -कोण -भुजा (SAS कसौटी)
कोण -भुजा- कोण (ASA कसौटी)
कोण -कोण भुजा (AAS कसौटी)
भुजा -भुजा -भुजा सर्वांगसमता (SSS कसौटी )
समकोण -कर्ण -भुजा सर्वांगसमता (RHS कसौटी )
प्रमेय 7.4
यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
दिया है : ΔABCऔर ΔDEF में, AB = DE, BC = EF और AC =DF
सिद्ध करना है : ΔABC≅ΔDEF
रचना : माना BC सबसे बड़ी भुजा है। रेखाखण्ड AG इसप्रकार खींचा कि EG = AB और ∠FEG=∠CBA हो । GF और DG को मिलाया।
प्रमाण : ΔABC और ΔGEF में ,
AB = GE [रचना से ]
∠FEG=∠CBA [रचना से ]
BC = EF [दिया है ]
∴ ΔABC≅ΔGEF [SAS सर्वांगसमता से ]
∴∠A=∠EGF [CPCT] ....(1)
और AC = GF [CPCT] ....(2)
अब AB = GE [रचना से ]
तथा AB = DE [दिया है ]
∴ GE = DE ...(3)
इसीप्रकार GF = DF .....(4)
अब ΔEDG में DE= GE [समी (3) से ]
∴ ∠1=∠2 [बराबर भुजाओं के सम्मुख कोण ] ....(5)
ΔDFG में DF= GF [समी (4) से ]
∴ ∠3=∠4 [बराबर भुजाओं के सम्मुख कोण ] ....(6)
∴∠1+∠3=∠2+∠4 [समी (5) व (6)से ]
∴ ∠EDF=∠EGF ....(7)
लेकिन ∠A=∠EGF [समी (1) से ]
∴∠A=∠EDF .....(8)
अब ΔABCऔर ΔDEF में
AB = DE [दिया है ]
AC = DF [दिया है ]
∠A=∠EDF [समी (8) से ]
∴ ΔABC≅ΔDEF [ SAS सर्वांगसमता से ]
सर्वांगसमता की इस कसौटी पर आधारित दो सर्वांगसम त्रिभुज निम्न प्रकार से होंगे - 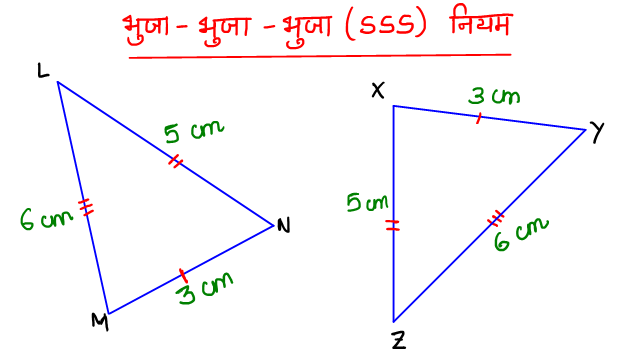
प्रमेय 7.5
यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमश: दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं। (इसे हम RHS समकोण (Right angle) - कर्ण (Hypotenuse) - भुजा (Side) सर्वांगसमता नियम से भी जानते हैं।)
दिया है : ΔABCऔर ΔDEF में, ∠B=∠E=90∘,
AB = DE और AC =DF
सिद्ध करना है : ΔABC≅ΔDEF
रचना : FE को G तक बढ़ाया ताकि EG = BC हो। DG को मिलाया।
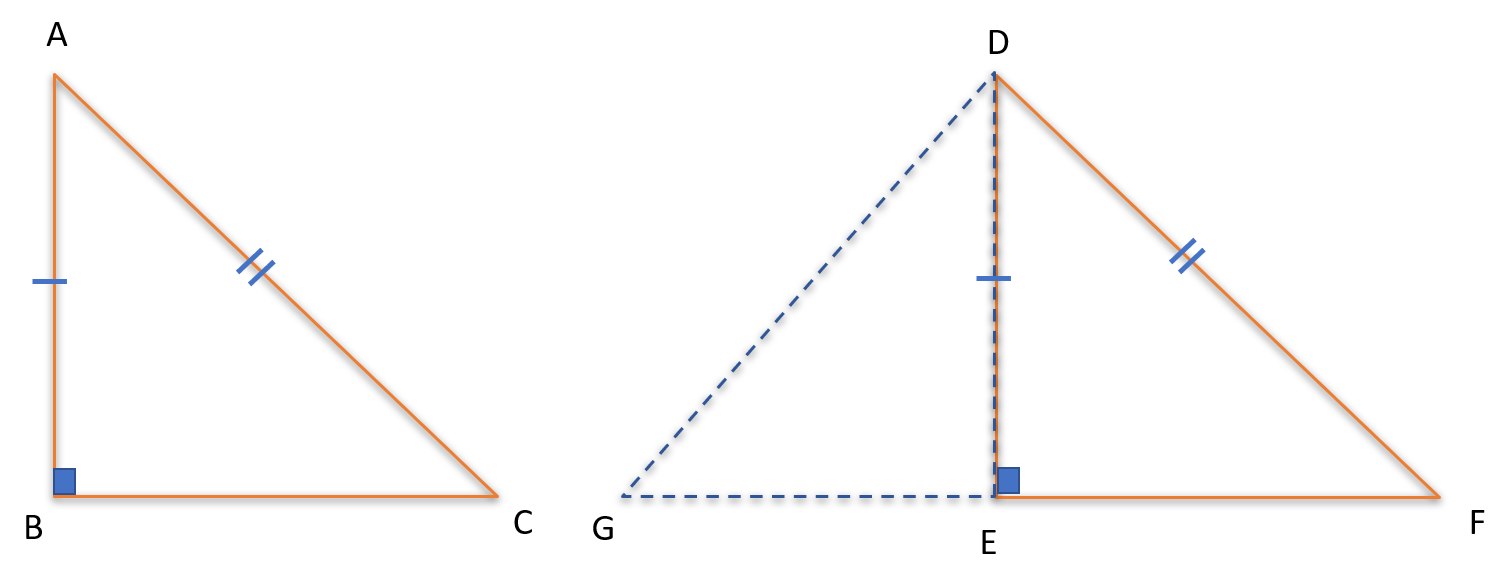
प्रमाण : ΔABC और ΔDEG में ,
AB = DE [दिया है ]
BC = EG [रचना से ]
∠B=∠DEG [ प्रत्येक 90∘ है ]
∴ ΔABC≅ΔDEG [SAS सर्वांगसमता से ]
∴∠C=∠G [CPCT] ....(1)
और AC = DG [CPCT] ....(2)
लेकिन AC = DF [दिया है ]
∴ DG = DF
∴ ∠G=∠F [बराबर भुजा के सम्मुख कोण ] .....(3)
अब ΔEDG में DE= GE [समी (3) से ]
∴ समी (1) और (3) से ∠C=∠F ....(4)
अब ΔABCऔर ΔDEF में ,
∠B=∠E[दिया है ]
∠C=∠F[समी (4) से ]
∴ ∠A=∠D .......(5)
पुनः ΔABCऔर ΔDEF में ,
AB = DE [दिया है ]
AC = DF [दिया है ]
∠A=∠D [समी (5) से ]
∴ ΔABC≅ΔDEF
[ SAS सर्वांगसमता से ]
सर्वांगसमता की इस कसौटी पर आधारित दो सर्वांगसम त्रिभुज निम्न प्रकार से होंगे -
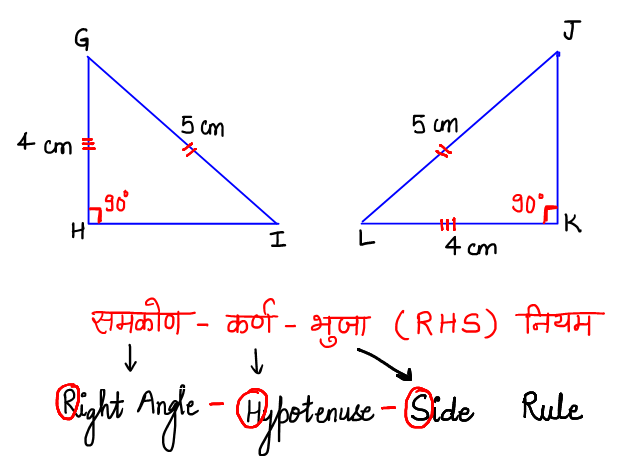
उदाहरण 6
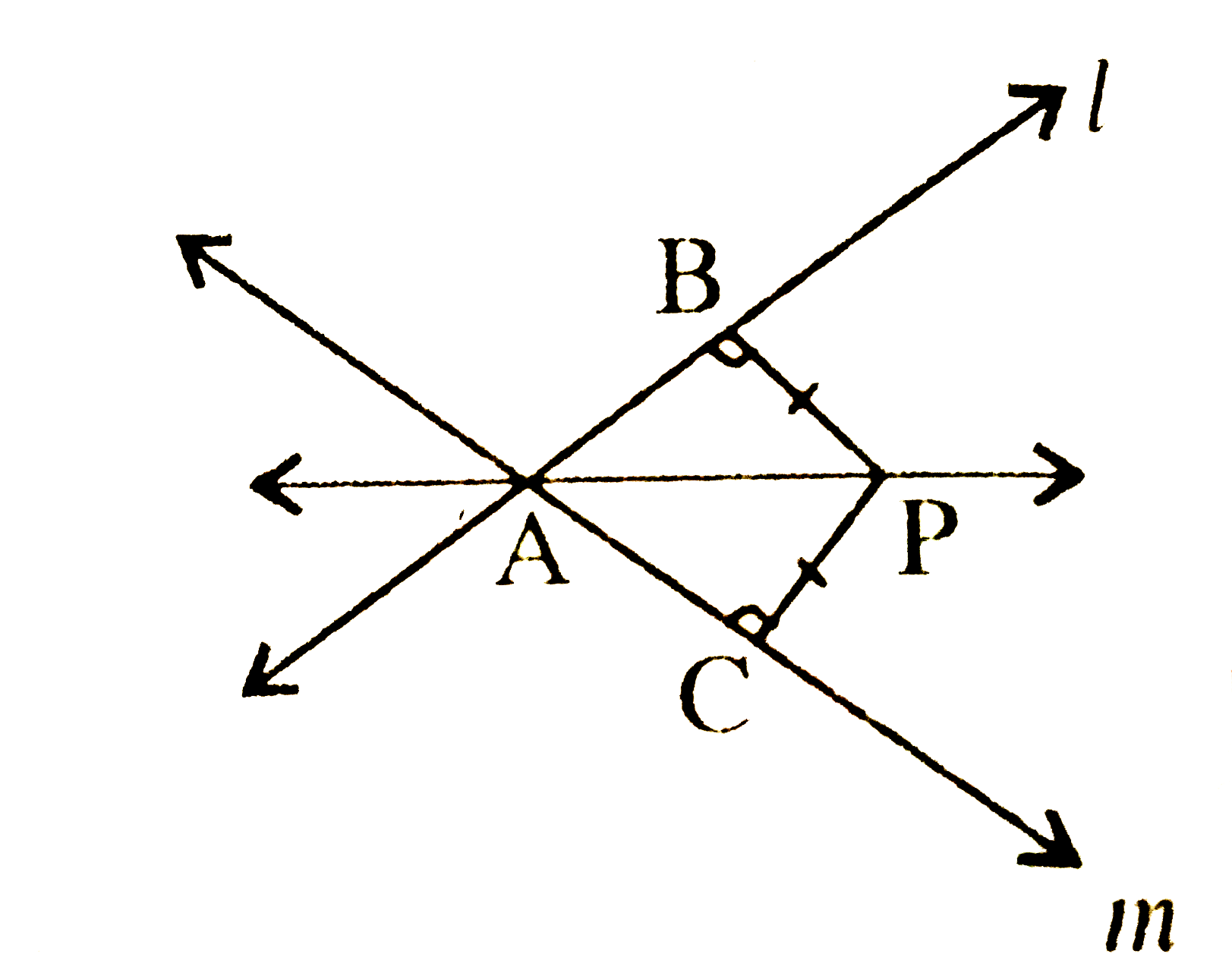
बिन्दु A पर प्रतिच्छेद करने वाली दो रेखाओं l और m से समदूरस्थ एक बिन्दु P है (देखिए चित्र) | दर्शाइए कि रेखा AP दोनों रेखाओं के बीच के कोण को समद्विभाजित करती है |
दिया है,
रेखाएँ l और m परस्पर A पर प्रतिच्छेद करती हैं |
PB_|_l" और "PC_|_m है
तथा PB=PC
सिद्ध करना है कि :
∠PAB=∠PAC
प्रमाण:
ΔPAB और ΔPAC में,
PB=PC
[ दिया है ]
PA=PA
[ उभयनिष्ठ ]
∠PBA=∠PCA=90∘
[दिया है]
अत: ΔPAB≅ΔPAC
[RHS नियम ]
∴∠PAB=∠PAC
[CPCT]
उदाहरण 7
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमश: एक-दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर हैं (देखिए चित्र) | दर्शाइए कि
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
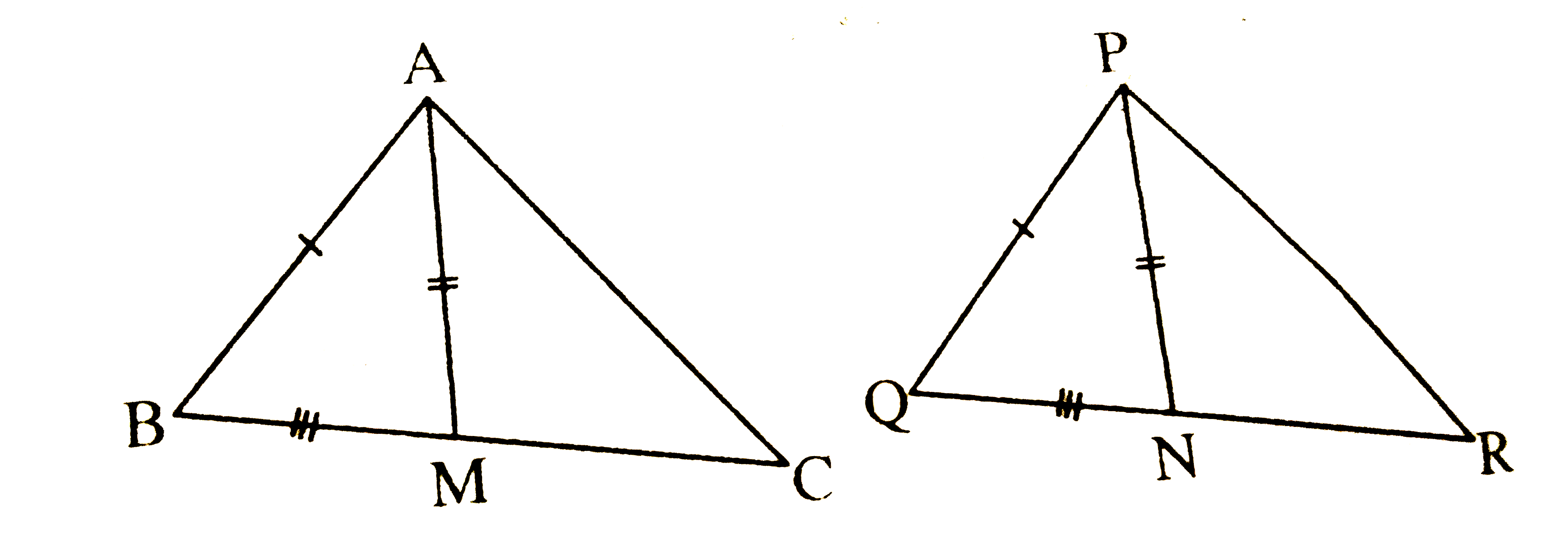
दिया है,
ABC तथा PQR दो त्रिभुज है जिनमें
AB=PQ
BC=QR
तथा माध्यिका AM = माध्यिका PN
सिद्ध करना है कि :
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
प्रमाण : (i)ΔABM तथा ΔPQN में
AB=PQ [दिया हैं ]
BM=QN
[चूंकि BC=QR∴12BC=12QR]
AM=PN [दिया हैं ]
(i) अत: ΔABM≅ΔPQN [SSS सर्वांगसमता ]
अब ΔABM≅ΔPQN
∴ ∠AMB=∠PNQ....(i)
लेकिन ∠AMB+∠AMC=∠PNQ+∠PNR=180∘ ......(ii)
[ रैखिक युग्म ]
(ii) में से (i) को घटाने पर,
∠AMC=∠PNR.......(iii)
(2) ΔAMCतथा ΔPMR में
AM=PN [दिया है ]
MC=NR
[∵BC=QR∴BC2=QR2]
तथा ∠AMC=∠PNR [(iii) से ]
अत:
ΔAMC≅ΔPNR
[SAS सर्वांगसमता से ]
∴ AC=PR[CPCT]...(iv)
अब
ΔABC तथा ΔPQR में,
AB=PQ
[ दिया है ]
BC=QR
[दिया है ]
तथा AC=PR [(iv) से ]
अत:
ΔABC≅ΔPQR
[SSS सर्वांगसमता ]
उदाहरण 8
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है | AP⊥BC खींच कर दर्शाइए कि ∠B=∠C है |
दिया है,
ABC एक समद्विबाहु त्रिभुज है जिसमें तथा AB = AC
सिद्ध करना है कि :
∠B=∠C.
बनावट :
AP⊥BC खींचा |
अब
ΔAPB और ΔAPC में,
AB=AC [दिया है ]
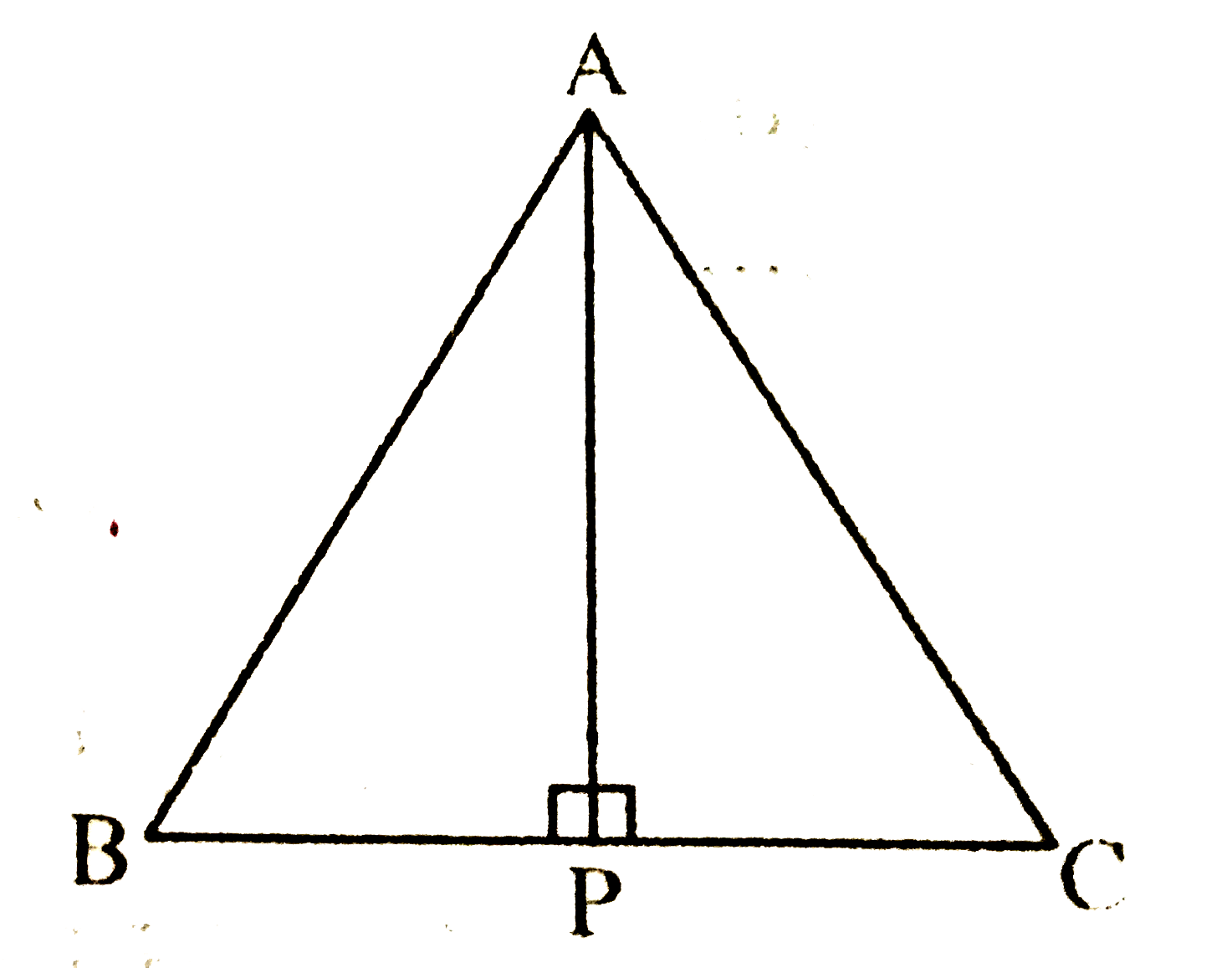
∠APB=∠APC=90∘
AP=AP [उभयनिष्ठ ]
अत:
ΔAPB≅ΔAPC
[ RHS नियम से ]
∴∠ABP=∠ACP
अर्थात
∠B=∠C.
एक त्रिभुज में असमिकाएँ
दोस्तों जैसे की अब तक हमने सर्वांगसमता के विषय में जाना , जिसमे हमने दो त्रिभुजों की भुजाओं और कोणों की समताओं (समिकाओं के बारे में पढ़ा है |)
अब यदि हमारे सामने कोई विषम बाहु त्रिभुज हो तो उस विषम बाहु त्रिभुज की भुजाओं आधार पर हम त्रिभुज के कोणों के बारे में क्या क्या बता सकते है ? आओं बच्चों अब इसके बारे में जानते हैं , और इसे हम एक महत्वपूर्ण प्रमेय से समझते हैं।
प्रमेय 7.6
यदि किसी त्रिभुज की दो भुजाएं असमान हो तो लम्बी भुजा के सामने का कोण बड़ा होता है।
दिया है : ΔABC में, AC>AB,
सिद्ध करना है : ∠ABC>∠ACB
रचना : भुजा AC पर बिन्दु D इसप्रकार लिया कि AB = AD । BD को मिलाया
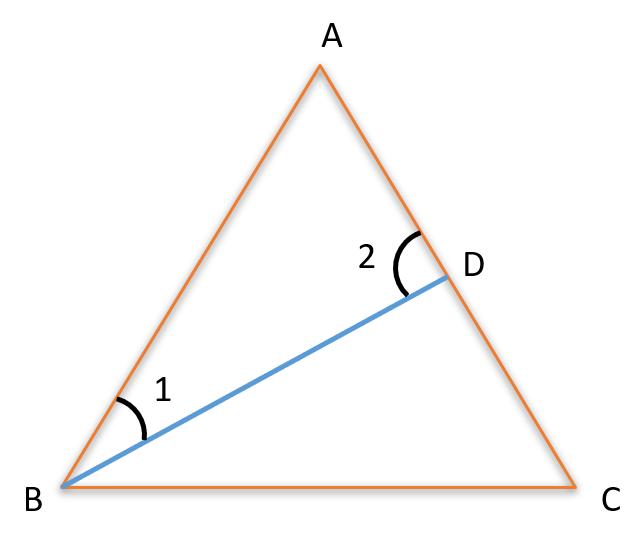
प्रमाण : ΔABD में AB = AD ,
∠1=∠2 [ समान भुजा के सम्मुख कोण ] .....(1)
लेकिन ∠2 ΔBCD का बहिष्कोण है
∠2>∠ACB [बहिष्कोण ] ....(2)
समी (1) और (2) से
∠1>∠ACB ....(3)
लेकिन ∠ACB>∠1 [रचना से ] ....(4)
समीकरण (3) और (4) से
∠ABC>∠ACB
प्रमेय 7.7
किसी त्रिभुज में बड़े कोण की सम्मुख भुजा बड़ी होती है।
दिया है : ΔABC में, ∠ABC>∠ACB
सिद्ध करना है : AC>AB
प्रमाण : △ABC में भुजाएँ AB तथा AC के लिए तीन संभावनाएँ हैं जिनमें केवल एक ही सत्य होगा
(i)AC=AB
(ii)AC<AB
(iii)AC>AB

स्थिति (i) : यदि AC = AB तो ∠ABC=∠ACB
लेकिन ∠ABC>∠ACB[दिया है ]
∴AC≠AB
स्थिति (ii) : यदि AC < AB तो
∠ACB>∠ABC [चूंकि बड़ी भुजा के सामने का कोण बड़ा होता है ]
लेकिन यह दिए गए तथ्य के विपरीत है।
AC cancel(lt) AB
स्थिति (iii) : हम सिद्ध कर चुके हैं कि AC≠AB तथा AC cancel(lt) AB तो केवल एक ही स्थिति शेष है अतः यह अवश्य ही सत्य होगा।
AC>AB
प्रमेय 7.8
त्रिभुज की किन्ही दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
सिद्ध करना है: AB+AC>BC
AB+BC>AC
BC+AC>AB
रचना : भुजा BA को बढ़ाया तथा AC = AD बनाया । CD को मिलाया।
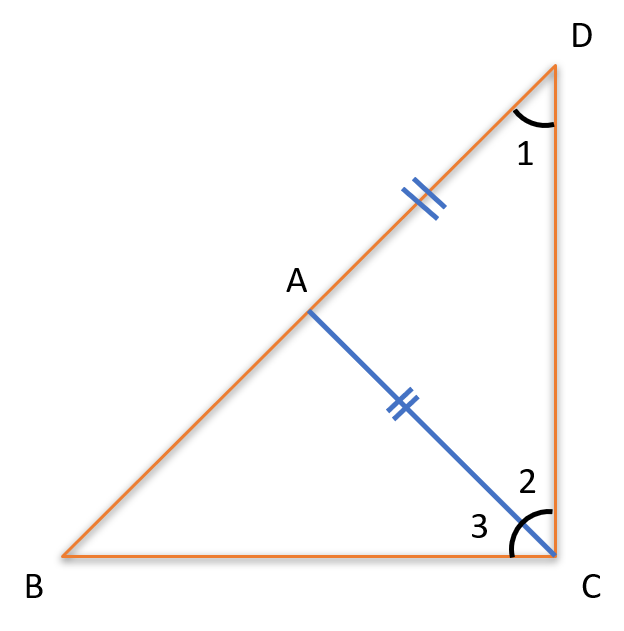
प्रमाण : ΔACD में, AC = AD [रचना से ]
∴ ∠2=∠1 [समान भुजा के सम्मुख कोण ]
∴(∠2+∠3) >∠1 या ∠BCD>∠1
, ΔBDC में,
∠BCD>∠1
BD>BC [बड़े कोण की सम्मुख भुजा बड़ी ]
BD = BA + AD =AB+AC [चूंकि AD = AC ]
(i) और (ii) से, AB + AC > BC
इसी प्रकार हम साबित कर सकते हैं कि
AB + BC > AC और BC + AC > AB
OMR (One Minute Revision)
- यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
- यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमश: दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं। इसे हम RHS समकोण (Right angle) - कर्ण (Hypotenuse) - भुजा (Side) सर्वांगसमता नियम से भी जानते हैं।
- यदि किसी त्रिभुज की दो भुजाएं असमान हो तो लम्बी भुजा के सामने का कोण बड़ा होता है।
- किसी त्रिभुज में बड़े कोण की सम्मुख भुजा बड़ी होती है।
- त्रिभुज की किन्ही दो भुजाओं का योग तीसरी भुजा से बड़ा होता है |
उदाहरण 9
सिद्ध करें कि समान कोणिक त्रिभुज समबाहु भी होता है |
हम जानते हैं यदि सम्मुख कोण बराबर हों तो सम्मुख भुजायें भी बराबर होती हैं
चूंकि ∠A=∠B,
∴ AC=BC ...(i)
चूंकि ∠B=∠C
∴ AB=AC ...(ii)
समी (i) और (ii) से
AB=BC=AC.
उदाहरण 10
दिये गये चित्र में , ΔPSR की भुजा SR पर एक बिंदु Q इस प्रकार है कि PQ = PR तो दिखाइये कि PS>PQ
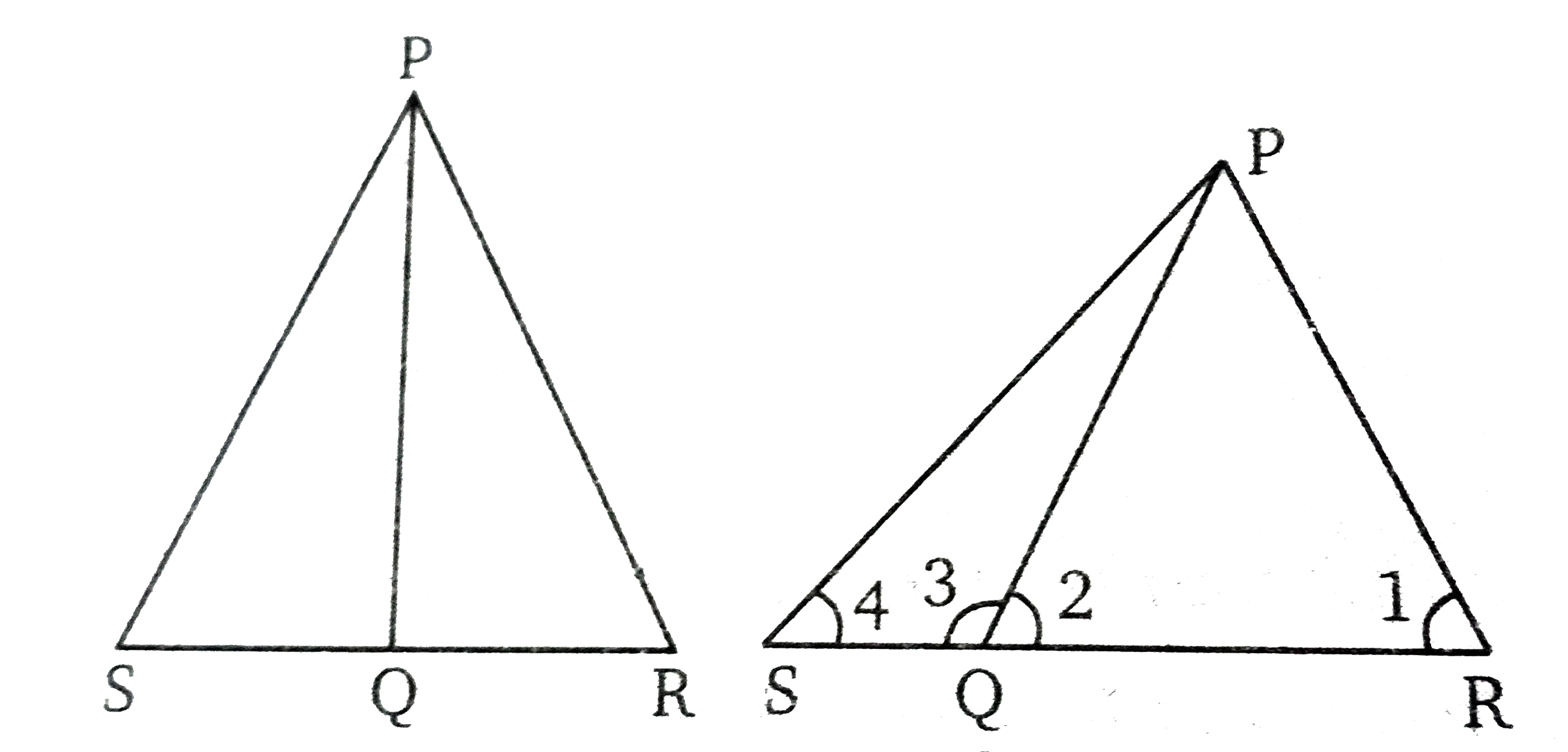
ΔPQR में दिया है कि
PQ = PR
⇒∠1=∠2
( चूंकि बराबर भुजाओं के सम्मुख कोण बराबर होते है ।)
तथा चूँकि एक त्रिभुज के बहिष्कोण , प्रत्येक अन्तःविपरीत कोण से बड़ा होता है ।
∴∠3>∠1
∠1=∠2का प्रयोग करने पर ∠3>∠2 ....(1)
अब ΔPQR में ∠2>∠4 ....(2)
(1)व (2) से
∠3>∠2>∠4
⇒∠3>∠4
चूंकि बड़े कोण की सम्मुख भुजा बड़ी होती है । इसलिए
PS>PQ
उदाहरण 11
दी गई आकृति में ΔABC की भुजाएँ AB तथा AC क्रमश: P एवं Q तक बढ़ायी गई है एवं ∠PBC<∠QCB है | सिद्ध करें की AC>AB.
चूँकि किसी त्रिभुज का बहिष्कोण सुदूर अन्त: कोणों के योगफल के बराबर होता है |
अत: बहिष्कोण ∠PBC=∠A+∠ACB
एवं बहिष्कोण ∠QCB=∠A+∠ABC
लेकिन दिया गया है की
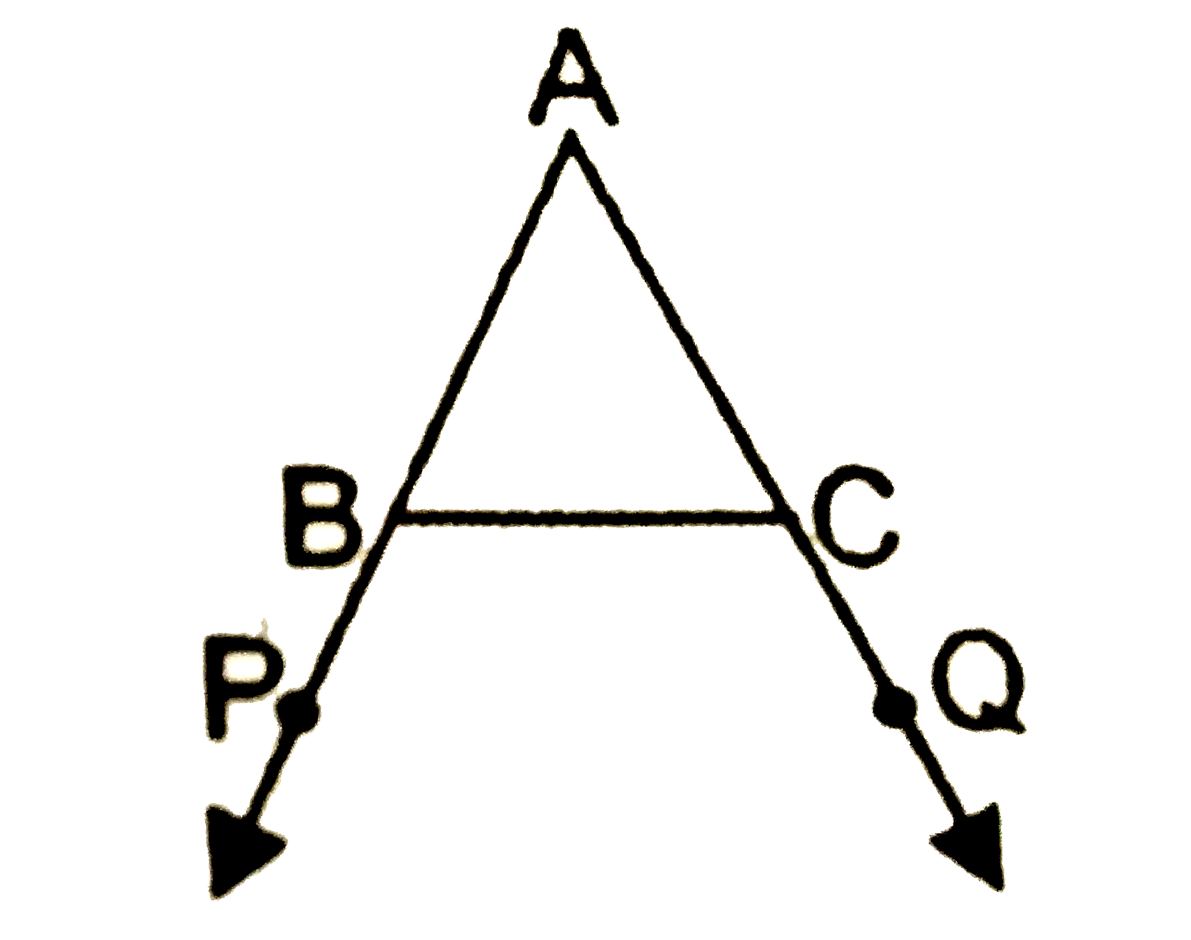
∠PBC<∠QCB
∴ ∠A+∠ACB<∠A+∠ABC
या, ∠ACB<∠ABC
∴ AB<AC
[त्रिभुज में छोटे कोण के सामने की भुजा छोटी होती है]
या, AC>AB
उदाहरण 12
ΔABC की भुजा BC पर D एक ऐसा बिंदु है कि AD=AC है (देखिए आकृति) दर्शाइए कि AB>AD है |
ΔDAC में,
AD=AC
इसलिए, ∠ADC=∠ACD
[बराबर भुजाओं के सम्मुख कोण]
अब, ∠ADC त्रिभुज ABD का एक बहिष्कोण है |
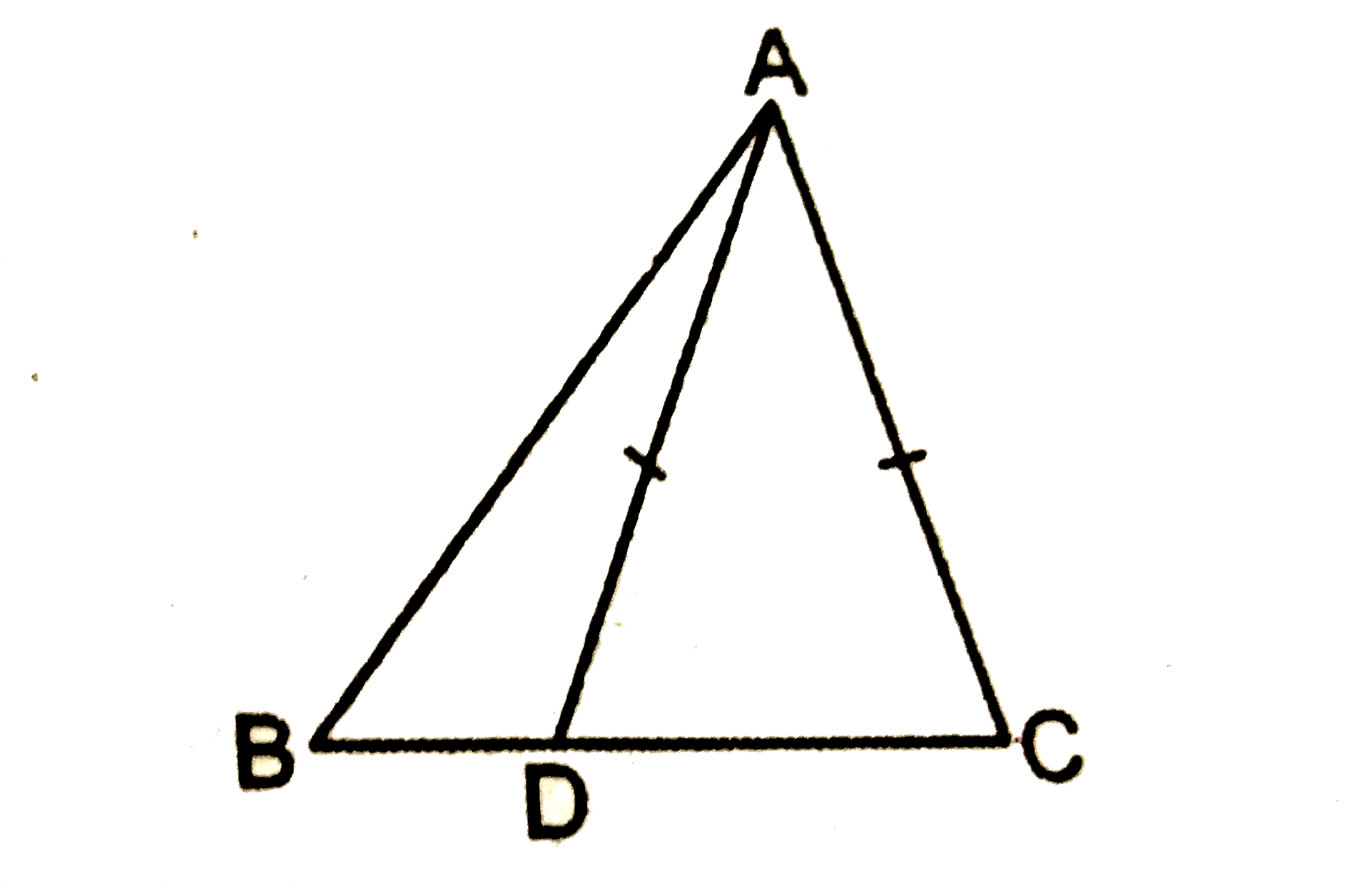
इसलिए, ∠ADC>∠ABD
या, ∠ACD>∠ABD
या, ∠ACB>∠ABC
[चूंकि ∠ADC=∠ACD]
अत:, AB>AC
[ΔABC में बड़े कोण की सम्मुख भुजा]
या, AB>AD
[चूंकि AD=AC]
उदाहरण 13
सिद्ध करें कि त्रिभुज कि किन्हीं दो भुजाओं का योग तीसरी भुजा कि माध्यिका के दुगुने से अधिक है |
माना कि ΔABC का मध्य बिन्दु D है तथा AD माध्यिका है |
सिद्ध करना है : AB+AC>2AD
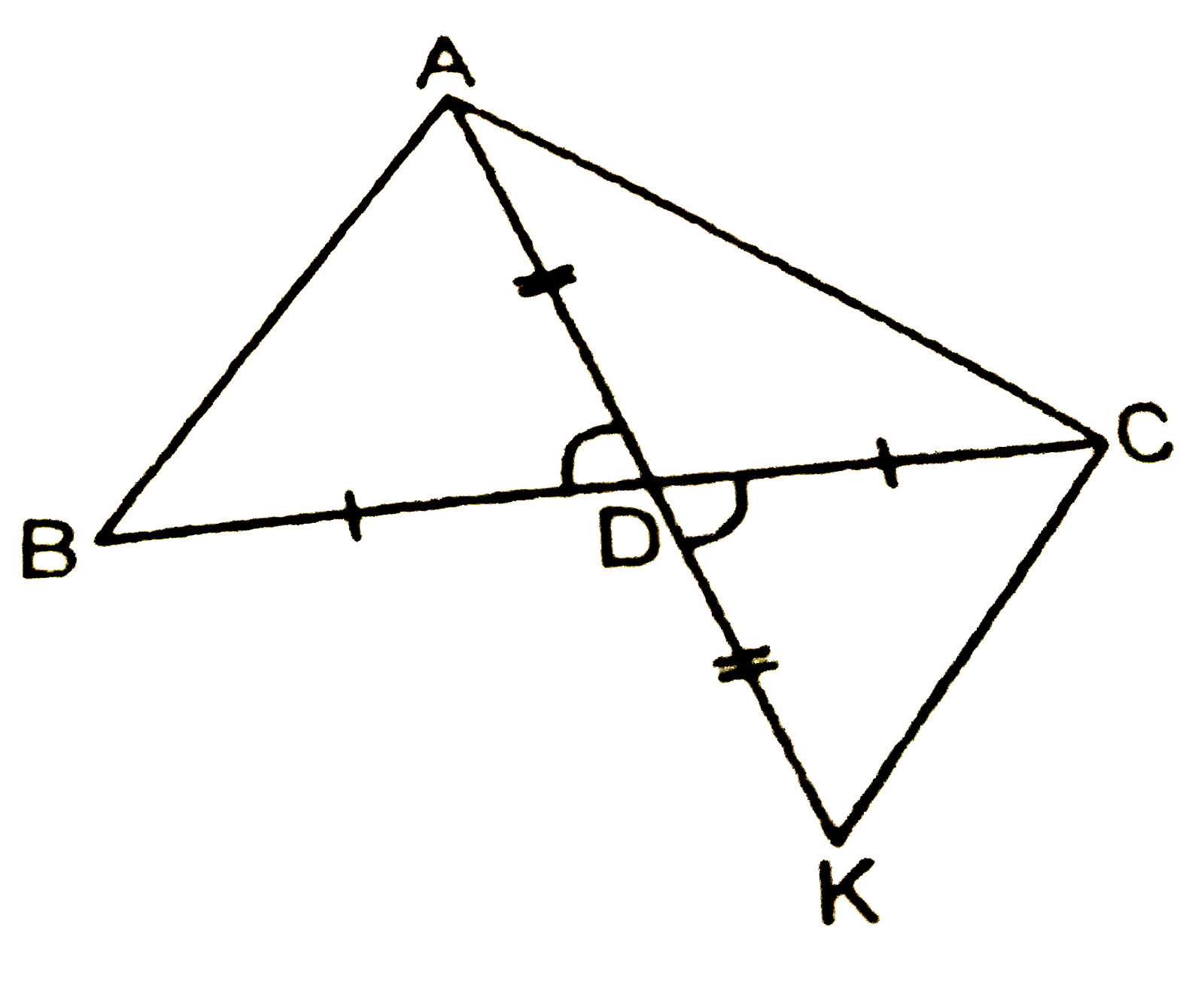
बनावट : AD को बढ़ाकर AD = DK बनाया | CK को मिलाया |
प्रमाण : ΔABD और ΔDKC में,
AD=DK
BD=DC
∠ADB=∠KDC
∴ΔABD≅ΔKCD
[SAS सर्वांगसमता]
∴AB=CK
अब ΔAKC में,
AC+CK>AK
∴AC+AB>AK
या, AC+AB>AD+DK
या,
AB+AC>AD+AD
∴ AB+AC>2AD
सारांश
इस अध्याय में, आपने निम्न बिंदुओं का अध्ययन किया है:
1. दो आकृतियाँ सर्वांगसम होती हैं, यदि उनका एक ही आकार हो और एक ही माप हो।
2. समान त्रिज्याओं वाले दो वृत्त सर्वांगसम होते हैं।
3. समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।
4. यदि त्रिभुज ABC और PQR संगतता A↔P, B↔Q और C↔R, के अंतर्गत सर्वांगसम हों, तो उन्हें सांकेतिक रूप में △ABC ≅ △PQR लिखते हैं।
5. यदि एक त्रिभुज की दो भुजाएँ और अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और अंतर्गत कोण के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।
6. यदि एक त्रिभुज के दो कोण और अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और अंतर्गत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।
7. यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।