Statements: All lines are circles. Some circles are squares. Conclusions: I. No square is a line. II. Some squares are definitely not circles.
1 1
2 2
3 3
4 4
Answer : 5. "5"
Related Solutions
Statements: Some squres are circles No circles is a triangle. No line is a square . Conclusions: I. No triangle is a square II. No line is a circle
View SolutionStatements: Some squres are circles
No circles is a triangle.
No line is a square .
Conclusions: I. All squres can never be triangles
II. Some lines are circles
View SolutionStatements:-
Some squares are circles.
No circle is a triangle.
Conclusions:-
I. some triangle is a square
II. No triangle is a square
View SolutionStatements: All squares are circles. No circle is cone. No circles is cone some cones are spheres.some rectangles are circles Conclusions: I Some rectangles are not cones II. No square is cone
View SolutionStatements:
All rings are circles
All squares are rings.
No.ellipse is a circle.
Conclusions: I. Some rings being ellipse is a possibility.
II. At least some circles are squres.
View SolutionStatements: All squares are triangles No triangles is circle All circles are rectangles Conclusions: I. No rectangles is square II. All rectangles being square is a possibility
View SolutionStatements: Some rings are cicles. No circle is a square Conclusions: I. No ring is a squre II. All rings are squres
View SolutionStatements: All squares are circles. No circle is cone. Some cones are spheres. Some rectangle are circles
Conclusions:
I. All rectangles being cones is a possibility
II. All rectangle being sphere is a possibility
View SolutionStatements:
All rings are circles
All squares are rings.
No.ellipse is a circle.
Conclusions: I. Some rings being ellipse is a possibility.
II. At least some circles are squres.
View SolutionStatements - Some lines are circles All circles are balls Conclusions (I) All balls being lines is a possibility (II) There is a possibility that some balls are neither circles nor lines
View SolutionIn each of the questions below. Two/three statements are given followed by conclusions/group of conclusions numbered and II. You have to assume all the statements to be true even if they seem to be at variance from the commonly known facts and then decide which of the given two conclusions logically follows from the information given in the statements.
Statements
A. Some squares are circles.
B. No circle is a triangle.
C. No line is a square.
Conclusions
I. All sqares can never be triangles.
II. Some lines are circles.
View SolutionStatements:- No squares are rectangles. All rectangles are triangles. Conclusions:- I. Some triangles are squares. II. Some triangles are rectangles.
View SolutionIn the following question below are given some statements followed by some conclusions. Taking the given statements to be true even if they seem to be at variance from commonly known facts, read all the conclusions and then decide which of the given conclusion logically follows the given statements. Statements : I. No circle is square. II. Some squares are rectangles. Conclusions: I. Some circles are rectangles. II. No circle is rectangle.
View SolutionDirection: In the question below are given three statements followed by two conclusions numbered I and II. You have to take the given statements to be true even if they seem to be at variance with commonly known facts. Read all the conclusions and then decide which of the given conclusions logically follows from the given statements disregarding commonly known facts. Statements: Some circle are square. Only a few square are rectangle. All circle are triangle. Conclusions: All rectangle being circle is a possibility. Some square are triangle.
View SolutionLook at the picture of the circle and answer the following question: The point O is the circle square . OQ is the straight line of the circle square . PQ is the straight line of the circle square .OP straight line is the circle square . MN is the straight line of the circle square The points M and N are two circles square SR is part of a circular field bounded by SR circle, SO and RO radius. square .PQ is the point at which the diagonal divides two circles into two equal parts square ।
View Solutionनिम्नलिखित प्रश्न में कुछ कथनों के बाद चार निष्कर्ष दिए गए हैं। आपको दिए गए कथनों को सच मानना होगा, भले ही, वे सामान्यतः ज्ञात तथ्यों से भिन्न हों। सभी निष्कर्षों को पढ़ें और तय करें कौन-सा निष्कर्ष सामान्यतः ज्ञात तथ्यों की परवाह किए बिना तर्कसंगत रूप से कथनों का अनुसरण करता है।
कथन : सभी वर्ग वृत्त हैं।
कुछ आयत वृत्त हैं।
कुछ त्रिकोण आयत हैं।
सभी त्रिकोण षट्भुज हैं।
निष्कर्ष: I कुछ त्रिकोण वृत्त हैं।
II. कुछ आयत षट्भुज हैं।
III कुछ त्रिकोण आयत और वृत्त दोनों है।
IV. कुछ वर्ग षट्भुज हैं।
View SolutionStatements: Some squares are parallelogram. No parallelograme is a triangle. No rhombus is a square Conclusions: (I) All squres can never be triangle (II) Some rhombus are parallelograme
View SolutionIf the circumference of a circle and the perimeter of a square are equal, then:
(A) Area of the circle = Area of the square
(B) Area of the circle Area of the square
(C) Area of the circle Area of the square
(D) Nothing definite can be said about the relation between the areas of the circle and square.
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
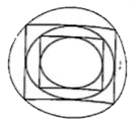
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?
View SolutionStatement:
1.Some quadrilaterals are squares.
2.All squares are rhombuses./
Conclusion/ :
I. No quadrilateral is a rhombus.
II. All rhombuses are squares.
III. Some quadrilaterals are rhombuses.
View Solution