Question

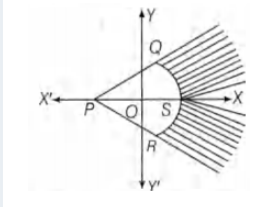
The shaded region where P = -1 0 Q = -1 + √2 √2 R = - 1 + √2 - √2 s = 1 0 is represented by

Text Solution

Verified by Experts

The correct option is a |z + 1| > 2 |arg z + 1| <π/4Explanation:Since |PQ | = |PS| =|PR| = 2∴ Shaded part represents the extemal part of circle having centre -1 0 and radius 2As we know equation of circle having centre z0 and radius r is |z - z0|= rAlso argument of z + I with respect to positive direction of x-axis is π/4.

Related Solutions

The shaded region ,where $P = (- 1, 0) Q = (- 1 + \sqrt{2}, \sqrt{2})$
$R = (- 1 + \sqrt{2}, - \sqrt{2}), S = 1 (1, 0)$ is represent by

View Solution
The shaded region ,where $P = (- 1, 0) Q = (- 1 + \sqrt{2}, \sqrt{2})$
$R = (- 1 + \sqrt{2}, - \sqrt{2}), S = 1 (1, 0)$ is represent by

View Solution
$P (1, - 1, 2), Q (2, 0, - 1)$ तथा $R (0, 2, 1)$ द्वारा बने समतल के लम्बवत इकाई ................ सदिश है।
View Solution
Volume of the tetrahedron with vertices P(-1, 2, 0), Q(2, 1, -3), R(1, 0, 1) and S(3, -2, 3) is
View Solution
If the points $P (1, - 1, - 1), Q (3, 1, λ), R (0, 2, 1), S (- 2, 0, 1)$ are coplanar, then $λ =$
View Solution
For all positive values of p, q, r and s
$\frac{(p^{2} + p + 1) (q^{2} + q + 1) (r^{2} + r + 1) (s^{2} + s + 1)}{p q r s}$
cannot be less than
View Solution
For all positive values of p,q,r and s
$\frac{(p^{2} + p + 1) (q^{2} + q + 1) (r^{2} + r + 1) (s^{2} + s + 1)}{p q r s}$ cannot be less than
View Solution
Let a, p, q, r, $s \in R - {0}$ . If $3 a^{2} + 2 (\frac{1}{p} - \frac{1}{s}) a + \frac{1}{p^{2}} + \frac{2}{q^{2}} + \frac{2}{r^{2}} + \frac{1}{s^{2}} - 2 (\frac{1}{p q} + \frac{1}{q r} + \frac{1}{r s}) \leq 0$ for some real a, then p, q, r, s are in
View Solution
If P(0, 1, 2), Q(4, -2, 1) and R(0, 0, 0) are three
points, then $∠ P R Q$ is
View Solution
If P(0, 1, 2), Q(4, -2, 1) and R(0, 0, 0) are three
points, then $∠ P R Q$ is
View Solution
Prove that $| \begin{matrix} 1 & p & p^{2} - q r \\ 1 & q & q^{2} - r p \\ 1 & r & r^{2} - p q \end{matrix} | = 0$
View Solution
If r and s are roots of $x^{2} + p x + q = 0$ , then what is the value of $(1 / r^{2}) + (1 / s^{2})$ ?
View Solution
यदि $A = {p, q, r, s}$ तथा $B = {1, 2, 3}$ तो ज्ञात कीजिए कि A से B में कौन-सा सम्बन्ध फलन नहीं है ?
(i) $R_{1} = {(p, 1) (q, 2), (r, 1), (s, 2)} (i i) R_{2} = {(p, 1), (q, 1), (r, 1), (r, 1), (s, 1)}$
(iii) $R_{3} = {(p, 1), (q, 2), (p, 2), (s, 3)} (i v) R_{4} = {(p, 2), (q, 3), (r, 2), (s, 2)}$
View Solution
If cos^(-1)p+cos^(-1)q+cos^(-1)r=pi(0<=p,q,r<=1) then the value of p^(2)+q^(2)+r^(2)+2pqr is
View Solution
The incentre of triangle whose vertices are $P (0, 2, 1), Q (- 2, 0, 0), R (- 2, 0, 2)$
View Solution
The shaded region, where $P = (- 1, 0), Q = (- 1 + \sqrt{2}, \sqrt{2}) R = (- 1 + \sqrt{2}, - \sqrt{2}), S = (1, 0)$ is represented by Figure

$| z + 1 | > 2, ∣ a r g (z + 1) < \frac{π}{4}$
$| z + 1 | < 2, ∣ a r g (z + 1) < \frac{π}{2}$
$| z + 1 | > 2, ∣ a r g (z + 1) > \frac{π}{4}$
$| z + 1 | < 2, ∣ a r g (z + 1) > \frac{π}{2}$
View Solution
यदि p, q, r, s गुणोत्तर श्रेणी में हो, सिद्ध कीजिए कि $\frac{1}{p^{2} + q^{2}}, \frac{1}{q^{2} + r^{2}}, \frac{1}{r^{2} + s^{2}}$ भी गुणोत्तर श्रेणी में होंगे ।
View Solution
यदि p, q, r, s गुणोत्तर श्रेणी में हो, सिद्ध कीजिए कि $\frac{1}{p^{2} + q^{2}}, \frac{1}{q^{2} + r^{2}}, \frac{1}{r^{2} + s^{2}}$ भी गुणोत्तर श्रेणी में होंगे ।
View Solution
The value of $p$ and $q (p \neq 0, q \neq 0)$ for which $p, q$ are the roots of the equation $x^{2} + p x + q = 0$ are (a) $p = 1, q = - 2$ (b) $p = - 1, q = - 2$ (c) $p = - 1, q = 2$ (d) $p = 1, q = 2$
View Solution
Simplify ((1)/(p)+(1)/(q+r))/((1)/(p)-(1)/(q+r))xx(1+(q^(2)+r^(2)-p^(2))/(2qr))
View Solution

The shaded region where P = -1 0 Q = -1 + √2 √2 R = - 1 + √2 - √2 s = 1 0 is represented by

Related Solutions

Recommended Content