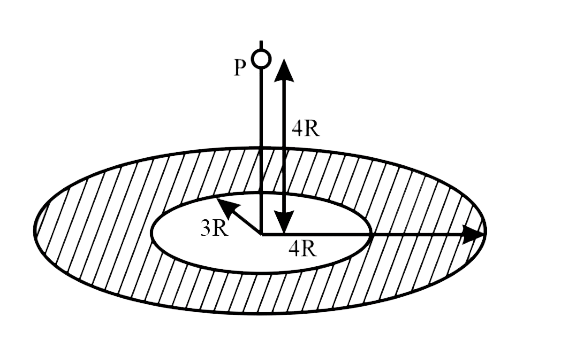
A thin uniform annular disc See figure of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is ……… A [2GM / 7R]4√2 – 5 B – [2GM / 7R]4√2 – 5 C GM / 4R D [2GM / 5R]√2 – 1
Correct option: A [2GM / 7R]4√2 – 5Explanation:The work required to take unit mass from P to infinity = – VP.where VP is gravitational potential at P due to discDividing disc into small elements each of thickness dr and dm. This element is at distance r from centre of disc. hencedm = [M × 2πr ∙ dr / {π4R2 – π3R2}] -------- where M is mass of disc.∴ dm = [2Mr ∙ dr / 7R2]VP = – 4R∫3R[G ∙ dm / {√r2 + 16R2}]= – 4R∫3R[G / {√r2 + 16R2}] × [2Mr dr / 7R2]= [– 2MG / 7R2] 4R∫3R[r ∙ dr / {√r2 + 16R21/2}]put r2 + 16R2 = x2 hence2r ∙ dr = 2x ∙ dxi.e. r dr = x ∙ dxwhen r = 3R x = √9R2 + 16R2 = 5Rr = 4R x = √16R2 + 16R2 = 4√2R∴ VP = [– 2GM / 7R2] G√2R∫5R dxVP = [– 2GM / 7R2]4√2 – 5R∴ – VP = [2GM / 7R]4√2 – 5 i.e. choice A.
Related Solutions
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
 View Solution
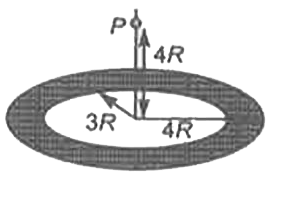
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
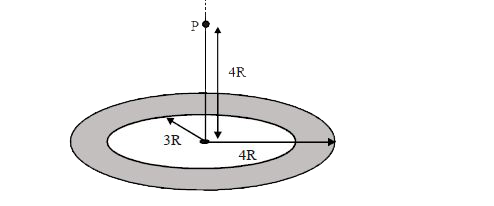
View Solutionजैसा कि चित्र में दिखाया गया है द्रव्यमान M की एक पतली एकसमान वलयाकार चकती की बाहरी त्रिज्या 4R और आंतरिक त्रिज्या 3R है। एक इकाई द्रव्यमान को इसकी अक्ष पर स्थित बिंदु P से अनंत तक ले जाने के लिए आवश्यक कार्य क्या है?
 View Solution
View SolutionThe external and internal radii of a thin uniform annular, disc (see figure) of mass M are 4R and 3R respectively, the work done in taking a unit mass to infinity at a point P on the axis of the disc is-
View SolutionM द्रव्यमान वाली एक पतली एकसमान वलयाकार डिस्क (चित्र देखिए) की बाह्य एवं आन्तरिक त्रिज्यायें क्रमश: 4R तथा 3R है। एक इकाई द्रव्यमान को डिस्क के अक्ष पर स्थित बिन्दु प के अनंत तक ले जाने में किया गया कार्य है
 View Solution
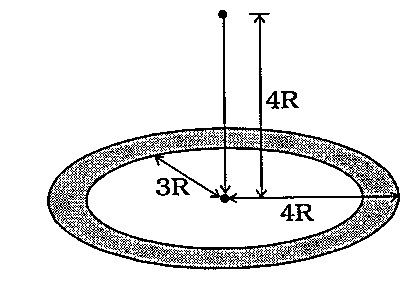
View Solutionएक पतली समरूप चकती का द्रव्यमान M, बाहरी त्रिज्या 4R एवं भीतरी त्रिज्या 3R है। एक इकाई द्रव्यमान को अक्ष पर स्थित बिन्दु P से अनन्त तक ले जाने के लिये कितने कार्य की आवश्यकता होगी।
 View Solution
View SolutionIf mass of earth is M ,radius is R and gravitational constant is G,then work done to take 1kg mass from earth surface to infinity will be (A) sqrt((GM)/(2R)) (B) (GM)/(R)] (C) sqrt((2GM)/(R))]
View SolutionThe intensity of gravitational field at the centre of a ring of mass m and radius R is (A) Zero (B)(Gm)/(2r^(2) (C) "(Gm)/(r^(2) (D) (2Gm)/(r^(2)
View Solutionપાતળી વર્તુળાકાર તકતીનું દળ M તથા બહારની ત્રિજ્યા 4R અને અંદરની ત્રિજ્યા 3R છે. અક્ષ પરના એકમ દળને P બિંદુએથી અનંત અંતરે લઈ જવા કરવું પડતું કાર્ય, ........ .
 View Solution
View SolutionFor a unit cell edge length = 5 Å , the element is of atomic mass 75, has denstiy of 2gm/cc. Calculate atomic radius of the element
View SolutionFor a unit cell edge length = 5 Å , the element is of atomic mass 75, has denstiy of 2gm/cc. Calculate atomic radius of the element
View SolutionProve that escape velocity from a planet sqrt(2GM//R) If M and R are the mass and radius of the planet, respectively.
View SolutionFind r if (i) 3r+1, 7r, 10r+8 are in G.P., (ii) 2r, 4r+1, 6r+2 are in G.P.
View SolutionA uniform metal sphere of radius and mass is surrounded by a thin uniform spherical shell of same mass and radius . The centre of the shell falls on the surface of the inner sphere. Find the gravitational fields at points and .
 View Solution
View SolutionA uniform metal sphere of radius and mass is surrounded by a thin uniform spherical shell of same mass and radius . The centre of the shell falls on the surface of the inner sphere. Find the gravitational fields at points and .
 View Solution
View SolutionA uniform metal sphere of radius and mass is surrounded by a thin uniform spherical shell of same mass and radius . The centre of the shell falls on the surface of the inner sphere. Find the gravitational fields at points and .
 View Solution
View SolutionIf in then must be (b) (c) (d)
View SolutionIf in then must be (b) (c) (d)
View SolutionIf in then must be (a) (b) (c) (d)
View Solution
