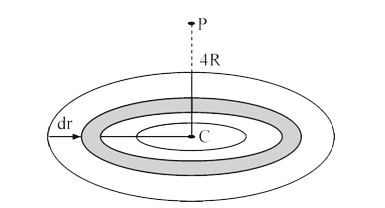
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

A

$\frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

B

$- \frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

C

$\frac{G M}{4 R}$

D

$\frac{2 G M}{5 R} (\sqrt{2} - 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Work required to take unit mass from infinity to point P = $V_{P}$ br> $∴$ Work required to take it from P to infinity = $- V_{P}$
To calculate $V_{P}$ , consider a ring element of radius r and width dr . Gravitational potential due to this ring at P is :
$d V_{P} = \frac{- G (d m)}{\sqrt{r^{2} + {(4 R)}^{2}}} = \frac{- G}{\sqrt{r^{2} + 16 R^{2}}} \frac{M (2 p r d r)}{(16 p R^{2} - 9 p R^{2})} = \frac{- 2 G M}{7 R^{2}} \frac{r d r}{\sqrt{r^{2} + 16 R^{2}}}$
$∴ V_{P} = \int d V_{P} = \frac{- 2 G M}{7 R^{2}} \int_{3 R}^{4 R} \frac{r d r}{\sqrt{r^{2} + 16 R^{2}}}$
Let $r^{2} + 16 R^{2} = t^{2} \Rightarrow 2 r \frac{d r}{d t} = 2 t \Rightarrow r d r = t d t$
$∴ \int \frac{r d r}{\sqrt{r^{2} + 16 R^{2}}} = \int \frac{t d t}{\sqrt{t^{2}}} = \int d t = t = \sqrt{r^{2} + 16 R^{2}}$
$∴ V_{P} = \frac{- 2 G M}{7 R^{2}} {[\sqrt{r^{2} + 16 R^{2}}]}_{3 R}^{4 R} = \frac{- 2 G M}{7 R^{2}} [\sqrt{32 R^{2}} - \sqrt{25 R^{2}}]$
$= \frac{- 2 G M}{7 R} (4 \sqrt{2} - 5) ∴ W_{reqd} = - V_{P} = \frac{2 G M}{7 R} (4 \sqrt{2} - 5)$

Updated on:21/07/2023

|

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-GRAVITATION-JEE Advance (Archive) SINGLE OPTION CORRECT

Home
Ask Doubt
Profile