Figure 10-Q2 shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval then a x = 2y b x = y c y = 2x d none of these.
c y = 2x Explanation: Both the pulleys have same angular speed hence the speed of the string supporting B will be twice that of A because of the double radius. So it will cover twice distance than A in the same time interval.
Related Solutions
Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then
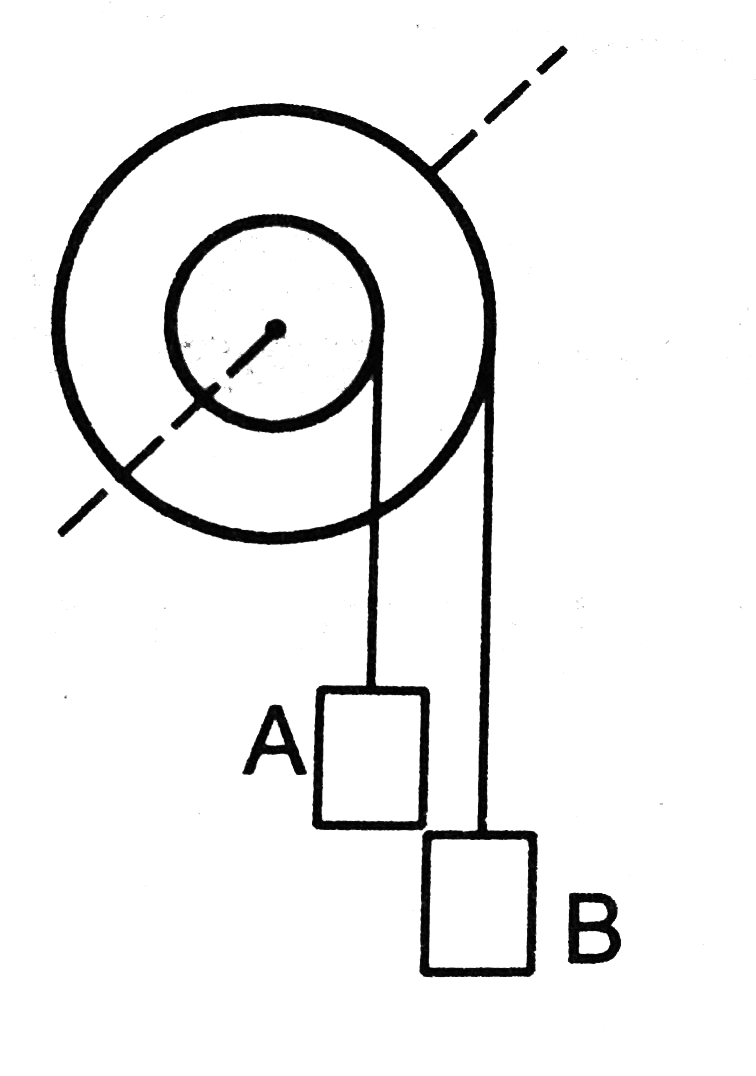
View SolutionFigure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then
View Solutionचित्र में एक छोटी घिरनी, दुगुनी त्रिज्या की एक बड़ी घिरनी के साथ जुड़ी है | दोनों के अक्ष एक ही है | यह निकाय उभयनिष्ठ अक्ष के परितः घूर्णन करता है | गुटकों A तथा B से जुडी डोरियाँ घिरनियों पर से जाती है तथा उन पर फिसलती नहीं है | यदि समान समय अवधि में A तथा B द्वारा चली गई दूरियाँ क्रमश: x तथा y हो, तो

View SolutionWheels and in Figure are connected by a belt that does not slip. The radius of is times the radius of . What would be the ratio of the rotational inertias if the two wheels had same angular momentum about their central axes.
 .
.
View SolutionA wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt to a wheel of radius 0.2 m (wheel B). The belt does not slip. By the time wheel B turn through 1 revolution, wheel A will rotate through:
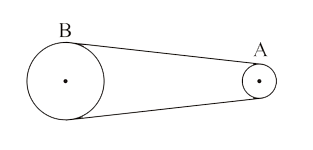
View SolutionA wheel of radius 0.1 m (wheel A) is attached by a non-stretching belt to a wheel of radius 0.2 m (wheel B). The belt does not slip. By the time wheel B turn through 1 revolution, wheel A will rotate through:

View SolutionGiven and is any line through it cutting the x-axis at If is perpendicular to and meets the y-axis in , then the equation of the locus of midpoint of is (a) (b) (c) (d)
View SolutionGiven A=(1,1) and A B is any line through it cutting the x-axis at Bdot If A C is perpendicular to A B and meets the y-axis in C , then the equation of the locus of midpoint P of B C is (a) x+y=1 (b) x+y=2 (c) x+y=2x y (d) 2x+2y=1
View SolutionGiven A-=(1,1) and A B is any line through it cutting the x-axis at Bdot If A C is perpendicular to A B and meets the y-axis in C , then the equation of the locus of midpoint P of B C is (a) x+y=1 (b) x+y=2 (c) x+y=2x y (d) 2x+2y=1
View SolutionGiven and is any line through it cutting the x-axis at If is perpendicular to and meets the y-axis in , then the equation of the locus of midpoint of is (a) (b) (c) (d)
View SolutionThe length of a rectangle is times its breadth . The area of the rectangle is: (a) (b) (c) (d) None of these
View SolutionGiven and is any line through it cutting the x-axis at If is perpendicular to and meets the y-axis in , then the equation of the locus of midpoint of is (a) (b) (c) (d)
View SolutionIn Figure, is a parallelogram and are points on the diagonal such that . Prove that is a parallelogram (ii) (iv)
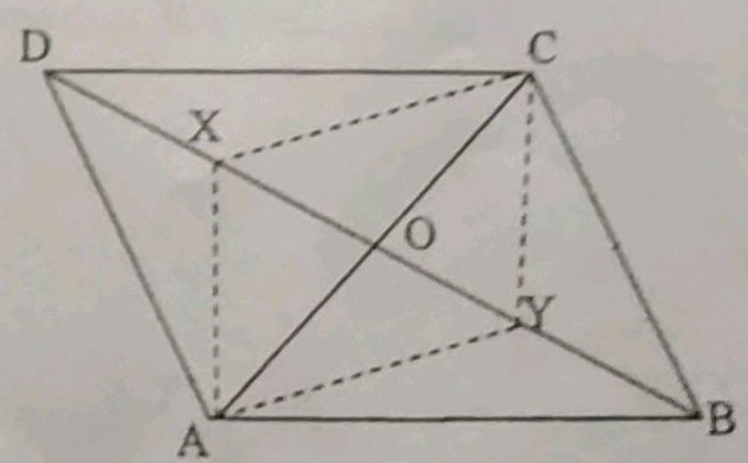
View SolutionIn Figure, is a parallelogram and are points on the diagonal such that . Prove that is a parallelogram (ii) (iv)
View SolutionConsider the parabola touching x-axis at (1,0) and y-axis (0,2). Directrix of parabola is : (A) (B) (C) (D)
View SolutionConsider the parabola touching x-axis at (1,0) and y-axis (0,2). Directrix of parabola is : (A) (B) (C) (D)
View SolutionShow that abs([x,b,c],[x,b,y],[y,b,c])=b(x-y)(c-y)
View SolutionThe solution of , is (A) (B) (C) (D) none of these
View SolutionThe solution of , is (A) (B) (C) (D) none of these
View Solution