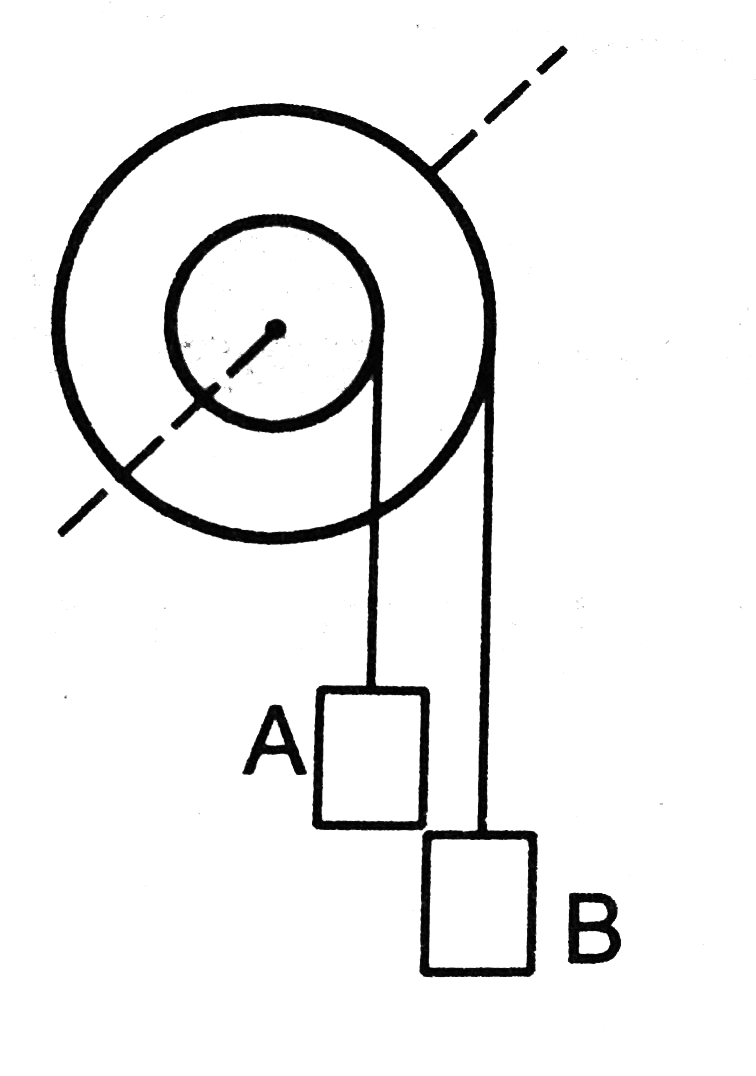
Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then
x=2y
x=y
y=2x
none of these
The correct Answer is:C
Step by step video, text & image solution for Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the comon axis. The strings supporting A and B do not slip on the wheels. If x and y be thedistances travelled by A and B in the same time interval, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
In the figure A and B are two blocks of mass 4kg and 2kg respectively attached to the two ends of light string passing overa disc C of mass 40kg and radius 0.1m. The disc is free to rotate about a fixed horizontal the string does not string does not slip over the disc. Find.
(i) The linear acceleration of mass B.
(ii) the number of revolutions made by the disc at the end of 10sec. from the start.
(iii) the tension in teh string segment supporting the block A.
 .
.
View SolutionA 4kg block is attached to a vertical rod by means of two strings of equal length. When the system rotates about the axis of the rod, the strings are extended as shown in figure.
(a) How many revolutions per minute must the system make in order for the tension in the upper string to be 200N ?
(b) What is the tension in the lower string then ?

View Solution
Knowledge Check
Figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then
 Ax = 2yBx = yCy = 2xDNone of these
Ax = 2yBx = yCy = 2xDNone of theseA wheel of radius R with an axle of radius R/2 is shown in the figure and is free to rotate about a frictionless axis through its centre and perpendicular to the page. Three forces (F, F, 2F) are exerted tangentially to the repective rims as shown in the figure.
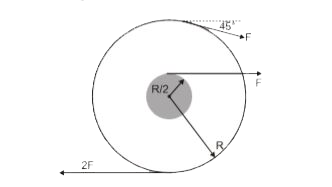
The magnitude of the net torque acting on the system is nearlyA3.5 FRB3.2 FRC2.5 FRD1.5 FR
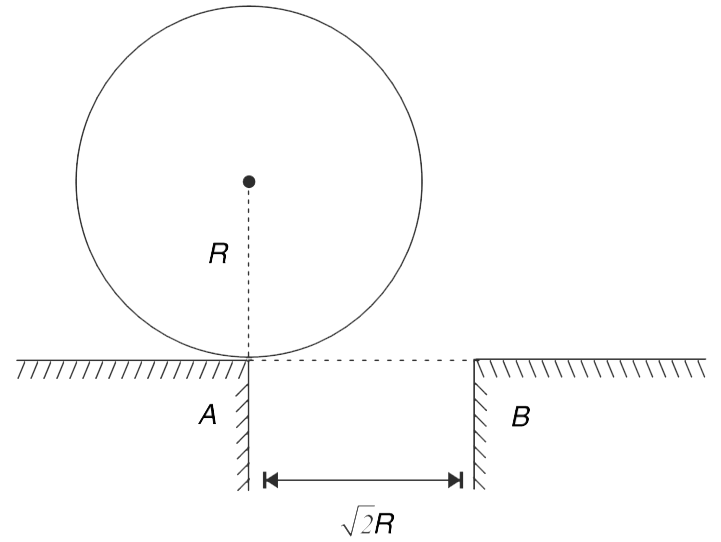
A disc of radius R stands at the edge of a table. If the given a gentle push and it beings to fall. Assume that the disc does not slip at A and it rotates about the point as it falls. The falling disc hits the edge of another table placed at same height as the first one at a horizontal distance of √2R. Imagine that the disc hits the edge B and rotates (up) about the edge
(a) Find the speed of the centre of the disc at the instant just before it hits the edge B.
(b) Find the angular speed of the disc about B just after the hit.
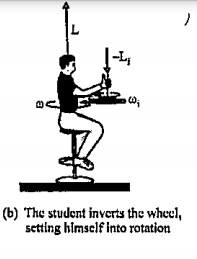
View SolutionFigure shows a student, sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose moment of inertia is I about its central axis. The wheel is rotating at an angular speed ωi from an overead perspective, the rotation is counter clockwise. The axis of the wheel point vertical, and the angular momentum →Li of the wheel points vertically upward. The student now inverts the wheel, as a result, the student and stool rotate about the stool axis. With what angular speed and direction does the student then rotate? (The moment of inertia of the student+stool+wheel system about the stool axis is I0)

View SolutionA constant net torque equal to 20 N-m is exerted on a pivoted wheel for 8 sec, during which time the angular velocity of the wheel increases from zero to 100 re/min. The external torque is then removed and the wheel is brought to rest by friction in its bearings in 70 sec. Compute (a) the moment of inertia of the wheel about the rotation axis, (b) the friction torque(c)thetotal no. of revolutions made by the wheel in the70 sec time interval
View SolutionA wheel of radius R having charg Q, uniformly distributed on the rim of the wheel is free to rotate about a light5 horizontal rod. The rod is suspended by light inextensible strings and a magnetic field B is applied as shown in the figure. The initial tensions in the strings are T0.Ifthebreak∈gtensionofthestr∈gsare(3T_(0))/(2),f∈dthemaxiμmanga––rvelocityomega_(0) with which the wheel can be rotated.
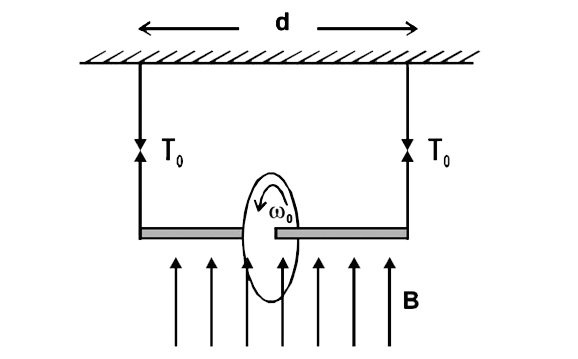
View SolutionFigure shows a student, again sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose rotational inertia Iwh about its central axis is 1.2kg⋅m2.
The wheel is rotating at an angular speed ωwh of 3.9 rev/s, as seen from overhead, the rotation is counterclockwise. The axis of the wheel is vertical, and the angular Momentum →Lwh of the wheel points vertically upward.
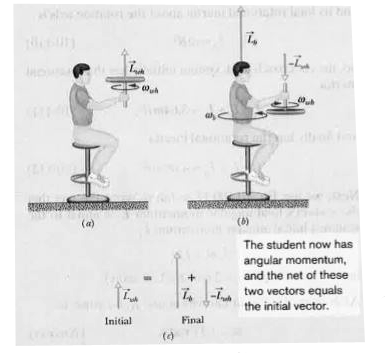
The student now inverts the wheel so that, as seen from overhead, it is rotating clockwise. Its angular momentum is now −→Lwh. The inversion results in the student, the stool, and the wheel's center rotating together as a composite rigid body about the stool's rotation axis, with rotational inertia Ib=6.8kg⋅m2. With what angular speed ωb and in what direction does the composite body rotate after the inversion of the wheel?
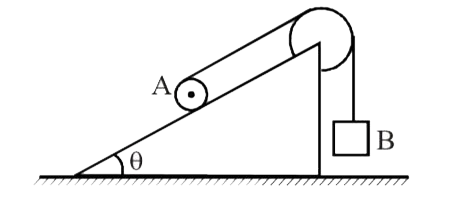
View SolutionIn the figure shown, a string is wound over a cylinder A. The other end of the string is attached to block B through a pulley. When the system is released the cylinder rolls down without slipping. The ratio of the magnitude of vertical component of displacement of A and B in any time interval t
View Solution
