A particular optical fibre consist of a glass core index of refraction n1 surrounded by a cladding index of refraction n2. n1 > n2. Suppose a beam of light enters the fibre from air at an angle θ with the fibre axis as shown in figure. Show that the greatest possible value θ for which a ray can be propagated down the fibre is given by. a θ = sin-1√n12 –n22 b θ = sin-1√n22 +n12 c θ = cos-1√n12 –n22 d θ = cos-1√n12 +n22
The correct Answer is:Option
Correct Option :- a θ = sin-1√n1 2 –n2 2 Explanation :-The situation is shown in figure. The light will be propagated down the fibre if it does not emerge from curved surface. i.e. at P. i > θc sin i > sin θc μ = μD/μr= n1/n2 sin θc = 1/μ = n2/n1 sin i > n2/n1 ....1 now from Snell’s law 1 sin θ =n1 sin r r + i = 90 r= 90 – i sin θ =n1 sin 90 - θ = n1 cos i cos i = sin θ /n1 sin i =√1- cos2i = √1- sin2 θ/n12 ........2 Substituting the value of sin i from equation 2 in equation 1 sin i = n2/n1 = √1- sin2 θ/n12 n2/n12 = 1- sin2 θ/n12 [n22 –n12/n12] ≤ - sin2 θ/n12 n2 2 –n1 2 ≤ - sin2θ θ ≤ sin-1 √n12 – n22 .......3
Related Solutions
Refractive index of cladding of optical fibre is ...... that of core of optical fibre.
View SolutionThe optical fibres have in an inner core of refractive index, and a cladding of refractive index no such that
View SolutionFor an optical fibre ,the ratio of the refractive index of the core to the refractive index of the cladding is 1.25 . What is the critical angle at the core cladding interface ?
View SolutionAn optical fibre having core of refractive index sqrt3 and cladding of refractive index 1.5 is kept in air. The maximum angle of acceptance is
View SolutionAn optical fibre having core of refractive index sqrt3 and cladding of refractive index 1.5 is kept in air. The maximum angle of acceptance is
View SolutionIn optical fibre refractive index of core is
View SolutionIn optical fibre refractive index of core is
View SolutionIn optical fibre refractive index of core is
View SolutionIn optical fibres, the refractive index of the core is
View SolutionIn optical fibre is refractive index of core greater than cladding or smaller ?
View Solutionλ1 wavelength light enters from the n1 refractive index to the n2 refractive index. What is the wavelength of that light in the second wavelength?
View SolutionThe glass of optical fibre has a refractive index 1.55 and cladding with another glass of refractive index 1.51. When the surrounding medium is air, the numerical aperture will be
View SolutionThe glass of optical fibre has a refractive index 1.55 and cladding with another glass of refractive index 1.51. When the surrounding medium is air, the numerical aperture will be
View SolutionThe optical fibres have an inner core of refractive index and a cladding of refractive index , such that
View SolutionAssertion (A): Propagation of light through an optical fibre is due to total internal reflection taking place at the core-clad interface. Reason (R): Refractive index of the material of the core of the optical fibre is greater than that of air.
View SolutionIn an optical fibre ,the refractive index of the core material is
View SolutionAn optical fibre consists of core of surrounded by a cladding of . A beam of light enters from air at an angle with axis of fibre. The highest for which ray can be travelled through fibre is

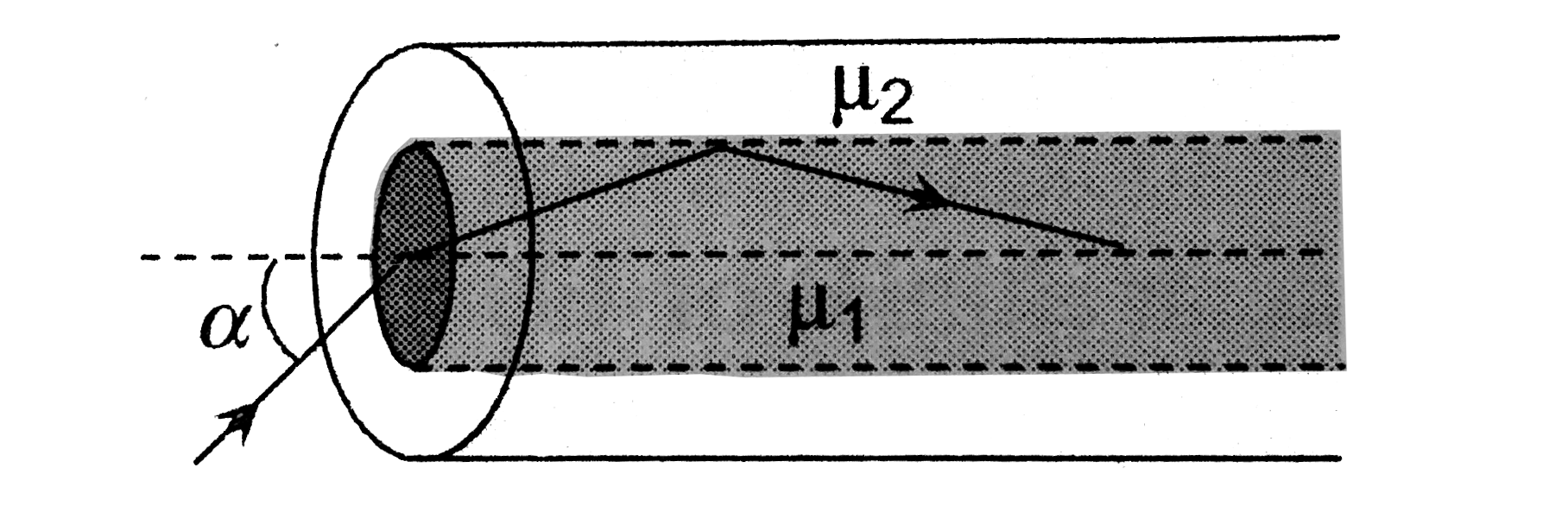
View SolutionAn optical fibre consists of core of mu_(1) surrounded by a cladding of mu_(2) lt mu_(1) . A beam of light enters from air at an angle alpha with axis of fibre. The highest alpha for which ray can be travelled through fibre is
View SolutionAn optical fibre consists of core of surrounded by a cladding of . A beam of light enters from air at an angle with axis of fibre. The highest for which ray can be travelled through fibre is
View Solution