A meniscus lens is made of a material of refractive index µ2 . Both its surfaces have radii of curvature R. It has two different media of refractive indices µ1 and µ3 respectively on its two sides shown in the figure. Calculate its focal length for µ1 < µ2 < µ3 when light is incident on it as shown.
For 1st surface
Related Solutions
A meniscus lens is made of a material of refractive index .Both its surfaces have radii of curvature .It has two different media of refractive indices and respectively ,on its two sides (See figure) .Calcualte its focal length for ,when light is incidence on it as shown
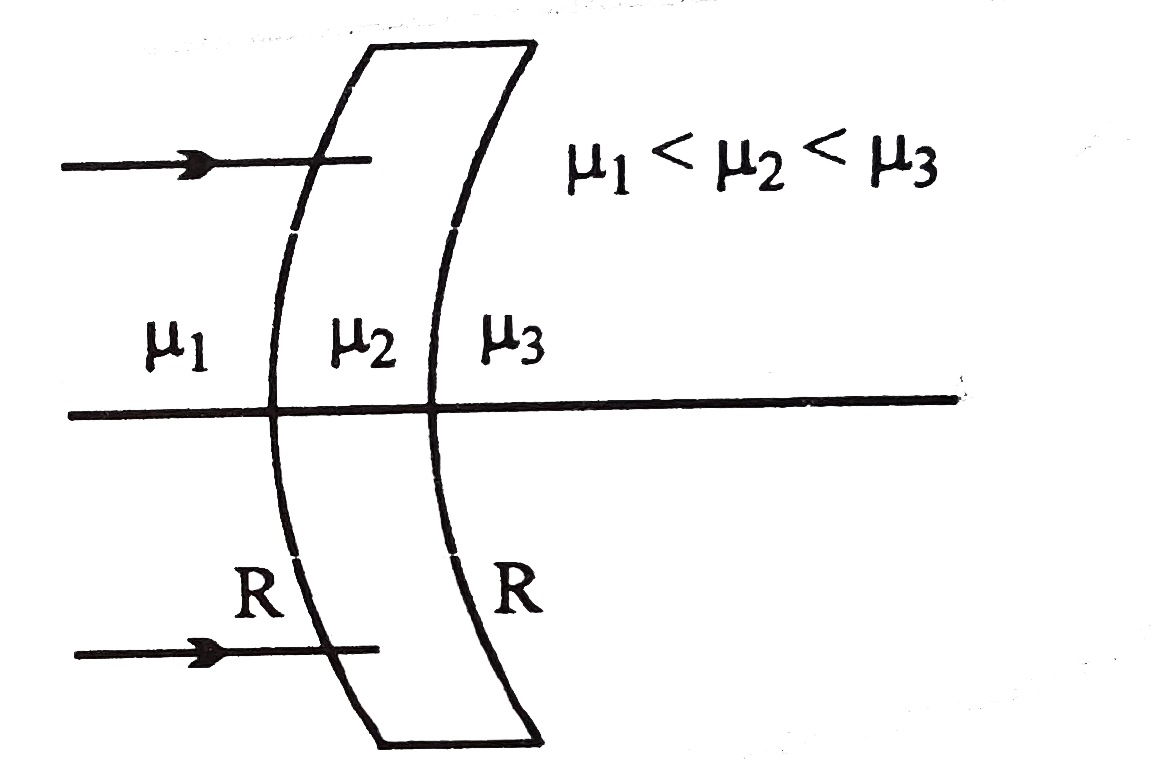
View SolutionA diverging meniscus lens of radii of curvatures 25cm and 50cm has a refractive index 1.5. Its focal length length is
View SolutionA convex lens (with material of refractive index of 3/2) has two surfaces of equal radii of curvature R. The magnitude of its focal length is
View SolutionA convex lens (with material of refractive index of 3/2) has two surfaces of equal radii of curvature R. The magnitude of its focal length is
View SolutionA diverging meniscus lens of radii of curvature 25cm and 50cm has a Refractive index 1.5. Its focal length is (in cm )
View SolutionLight is incident on the thin lens as shown in figure. The refractive index of the material of the lens is mu_(2) . The radii of curvature of both the surfaces are R. The refractive index of the medium of left side is mu_(1) , while that of right side is mu_(3) . What is the focal length of the lens?
View SolutionA biconvex lens made of glass (refractive index 1.5) has two spherical surfaces having radii 20cm and 30cm. Calculate its focal length.
View SolutionA concavo-convex lens is made of glass of refractive index 1.5. The radii of curvature of its two surfaces are 30 cm and 50 cm. Its focal length when placed in a liquid of refractive index 1.4 is
View SolutionA concavo-convex lens is made of glass of refractive index 1.5. The radii of curvature of its two surfaces are 30 cm and 50 cm. Its focal length when placed in a liquid of refractive index 1.4 is
View SolutionCalculate the focal length of a convex lens whose radii of curvature of two surfaces is 10cm and 15cm respectively and its refractive index is 1.5.
View SolutionSTATEMENT-1: A single lens will have two different focal lengths if the media on its two sides have different refractive indices. STATEMENT-2: The focal length of a lens can be defined in two different ways.
View SolutionThe focal length of an equiconvex lens in air i equal to either of its radii of curvature. The refractive index of the material of the lens is …........
View SolutionFocal length of the plano-convex lens is when its radius of curvature of the surface is R and n is the refractive index of the lens.
View SolutionFind the focal length of plano convex lens, when its radius of curvature of the surface is R and n is the refractive index of the lens?
View SolutionA biconvex lens of focal length f and radii of curvature of both the surface R is made of a material of refractive index n_(1) . This lens is placed in a liquid of refractive index n_(2) . Now this lens will behave like
View SolutionIf the radii of curvature of the two surfaces of a concave lens are 10 cm and 20 cm respectively and the refractive index is 1.5. What is its focal length ?
View SolutionThe radii of curvature of the two surface of a double convex glass lens are 10 cm and 20 cm respectively. If the refractive index of glass in 1.5, then its focal length will be
View SolutionA biconvex lens with equal radii curvature has refractive index 1.6 and focal length 10 cm. Its radius of curvature will be:
View SolutionA biconvex lens with equal radii curvature has refractive index 1.6 and focal length 10 cm. Its radius of curvature will be:
View SolutionA concave lens has the same radii of curvature for both sides and has a refractive index 1.6 in air. In the second case, it is immersed in a liquid of refractive index 1.4. Calculate the ratio of the focal lengths of the lens in two cases.
View Solution