Prove that the area of the triangle formed by the tangents at x1 y1 x2 y2 and x3 y3 to the parabola y2 = 4ax a > 0 is
Let Be three points on the parabola. y2 = 4ax a > 0 The equation of the tangents at D E and F are 1 – 2 ⇒ t1 – t2y = at1 – t2t1 + t2 ⇒ y = at1 + t2 substituting in 1 we get x = at1t2 ∴ The point of intersection of the tangents at D and E is say P[at1t2 at1+t2] Similarly the points of intersection of tangent at E F and at F D are Q[at2t3 at2+t3] and R[at3t1 at3+t1] respectively. Area of ∆PQR = Absolute value of
Related Solutions
-কে একটি তৃতীয় ক্রমের নির্ণায়কের আকারে লিখলে তা হবে-
View Solutionযদি a একক বাহুবিশিষ্ট সমবাহু ত্রিভুজের তিনটি শীর্ষ এবং হয় তবে প্রমাণ করো যে,
View SolutionProve that the incentre of the triangle whose vertices are given by A(x1,y1),B(x2,y2),C(x3,y3)is(ax1+bx2+cx3)/(a+b+c),(ay1+by2+cy2)/(a+b+c) where a b,and c are the sides opposite to the angles A,B and C respectively.
View SolutionThe co-ordinates of the vertices are A(x1,y1)B(x2,y2) and C(x3,y3). The line joining the points A and B is divided by a point P in the ratio 1:k and line joining by a point P in the point Q in the ratio m:k+1. Find co-ordinates of Q.
View SolutionIf is the mean of x1, x2,x2,x3, ………..xn , then the mean of x1+a,x2+a, x3+a...xn+a
View SolutionFind the equation of the radical axis of the following circles. is
View Solution2/9,3/9,4/9,5/9 The words in the parallel series of ......... x1,x2,x3 If you write ....... x1+,x2+,x3= ............
View SolutionThe number of integral solution of x1+x2+x3+x4=25, such that x1>=1,x2>=2,x3>=3,x4>=4
View Solution2.10 The radii of the circles x2 + y2 = 1, x2 + y2 – 2x – 6y = 6 and x2 + y2 - 4x - 12y = 9 are in(A)AP.(B)GP.(C) H.P.(D) None
View SolutionIf , then (cos^2x)y2-(1+sin2x)y1=0
View SolutionThe table given below shows the production of rice and the area under rice cultivation of a country for 5 consecutive years Y1, Y2, Y3, Y4 and Y5.
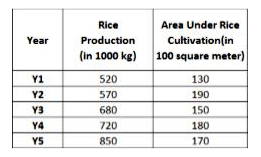
What is the yield per square meter for the year Y3?
View SolutionThe line chart given below show the ratio of imports to exports for a country for 5 consecutive years Y1, Y2, Y3, Y4 and Y5. If the exports for year Y3 is Rs.35000 crore, then what will be imports (in crores) for the year Y3?
View SolutionFind the third proportional to and (x+y)
View SolutionIf M is the mean of x1 , x2 , x3 , x4 , x5 and x6, prove that (x1 − M) + (x2 − M) + (x3 − M) + (x4 − M) + (x5 — M) + (x6 − M) = 0
View Solution(b)The coordinates of the point R which divides the line segment joining P(x1,y1,z1) and Q(x2,y2,z2) internally in the ratio m:n are given by…………
View SolutionIf y = sin px and y_n is the nth derivative of y , then find the value of |(y, y1, y2), (y3, y4, y5), (y6, y7, y8)|
View SolutionThe pair of straight lines x2 – 4xy + y2 = 0 together with the line form a triangle which is
View Solution. Find current enclosed in the loopMagnetic field at a point (x, y, z) is given by B- Boyix2 + y = 2(x2 + y2)2__Box(x2 + y2)2
View SolutionIf is the angle which the straight line joining the points subtends at the origin, prove that
View SolutionIf a x1 2+b y1 2+c z1 2=a x2 2+b y2 2+c z2 2=a x3 2+b y3 2+c z3 2=d ,a x2 3+b y_2y_3+c z_2z_3=a x_3x_1+b y_3y_1+c z_3z_1=a x_1x_2+b y_1y_2+c z_1z_2=f, then prove that |x_1y_1z_1x_2y_2z_2x_3y_3z_3|=(d-f){((d+2f))/(a b c)}^(1//2)
View Solution